day45第九章动态规划(二刷)
今日任务
- 70.爬楼梯(进阶)
- 322.零钱兑换
- 279.完全平方数
70.爬楼梯(进阶)
题目链接:
https://leetcode.cn/problems/climbing-stairs/description/
题目描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶提示:
1 <= n <= 45
题解代码:
class Solution {
public://二刷复习动态规划,用完全背包地方式做一次int climbStairs(int n){vector<int> dp(n+1, 0); //定义dp数组,dp[i]表示爬到有i个台阶的楼顶,有dp[i]种方法dp[0] = 1; //初始化dp数组,dp[0]是其他数值的基础,所以要是1for(int i = 1; i <= n; i++){//遍历背包for(int j = 1; j <= 2;j++){//遍历物品,也就是台阶if(i-j >= 0){dp[i] += dp[i-j];}}}return dp[n];}//一刷动态规划 /*int climbStairs(int n) {//再用完全背包的方式做一次 vector<int> dp(n+1,0);//定义dp数组,dp[i]表示爬到有i个台阶的楼顶,有dp[i]种方法dp[0] = 1; //初始化dp数组,dp[0]是其他数值的基础,所以要是1for(int i = 1; i <= n;i++){ //遍历背包for(int j = 1; j <= 2; j++){ //遍历物品,也就是台阶if(i-j>=0){dp[i] += dp[i-j];}}}return dp[n];/*if(n <= 1){return n; }vector<int> dp(n+1); //定义dp数组,dp[i]代表到第i层有dp[i]种办法dp[1] = 1; //初始化dp数组,注意这里不初始化dp[0]dp[2] = 2;for(int i = 3; i <= n; i++){//注意i是从3开始的dp[i] = dp[i-1] + dp[i-2];//递推方程}return dp[n];*//* }*///二刷复习动态规划//斐波那契数列式完成/*int climbStairs(int n){if(n <= 1){return n;}vector<int> dp(n+1); //dp数组,dp[i]代表到第i层有dp[i]种方法dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}*/
};
322.零钱兑换
题目链接:
https://leetcode.cn/problems/coin-change/description/
题目描述:
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins =[2], amount =3输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
题解代码:
class Solution {
public://二刷动规复习int coinChange(vector<int>& coins, int amount){vector<int> dp(amount+1, INT_MAX); //dp数组,dp[j]表示凑足总数为j所需要的钱币的最少个数为dp[j]dp[0] = 0; //初始化dp数组,dp[0]凑足总数为0所需的钱币最少个数为0个for(int i = 0; i < coins.size(); i++){//遍历物品for(int j = coins[i]; j <= amount; j++){//遍历背包if(dp[j-coins[i]] != INT_MAX){dp[j] = min(dp[j],dp[j-coins[i]]+1);}}}if(dp[amount] == INT_MAX){return -1;}return dp[amount];}//一刷动规复习/*int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1, INT_MAX); //dp数组,dp[j]表示凑足总数为j所需的钱币的最少个数为dp[j]dp[0] = 0;//初始化dp数组,dp[0]凑足总数为0所需的钱币的最少个数为0个for(int i = 0; i < coins.size(); i++){//遍历物品for(int j = coins[i]; j <= amount; j++){ //遍历背包if(dp[j-coins[i]] != INT_MAX){dp[j] = min(dp[j],dp[j-coins[i]]+1);}}}if(dp[amount] == INT_MAX){return -1;}return dp[amount];}*/
};
279.完全平方数
题目链接:
https://leetcode.cn/problems/perfect-squares/description/
题目描述:
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n =12输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n =13输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
题解代码:
class Solution {
public://二刷动规复习int numSquares(int n){vector<int> dp(n+1, INT_MAX); //定义dp数组,dp[j]表示和为j的完全平方数的最小数量dp[j]dp[0] = 0; //和为0的完全平方数的最小数量为dp[0]for(int i = 0; i <= n; i++){//遍历背包for(int j = 1; j*j <= i; j++){//遍历物品dp[i] = min(dp[i], dp[i-j*j]+1);}}return dp[n];}//一刷动规/*int numSquares(int n) {vector<int> dp(n+1,INT_MAX);//定义dp数组,dp[j]表示和为j的完全平方数的最小数量d[j]dp[0] = 0; //和为0的完全平方数的最小数量为dp[0]for(int i = 0; i <= n; i++){ //遍历背包for(int j = 1; j*j <= i; j++){ //遍历物品dp[i] = min(dp[i],dp[i-j*j]+1);}}return dp[n];}*/
};
总结
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关文章:
)
day45第九章动态规划(二刷)
今日任务 70.爬楼梯(进阶)322.零钱兑换279.完全平方数 70.爬楼梯(进阶) 题目链接: https://leetcode.cn/problems/climbing-stairs/description/ 题目描述: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不…...
第十四届蓝桥杯第三期模拟赛原题与详解
文章目录 一、填空题 1、1 找最小全字母十六进制数 1、1、1 题目描述 1、1、2 题解关键思路与解答 1、2 给列命名 1、2、1 题目描述 1、2、2 题解关键思路与解答 1、3 日期相等 1、3、1 题目描述 1、3、2 题解关键思路与解答 1、4 乘积方案数 1、4、1 题目描…...
client打包升级
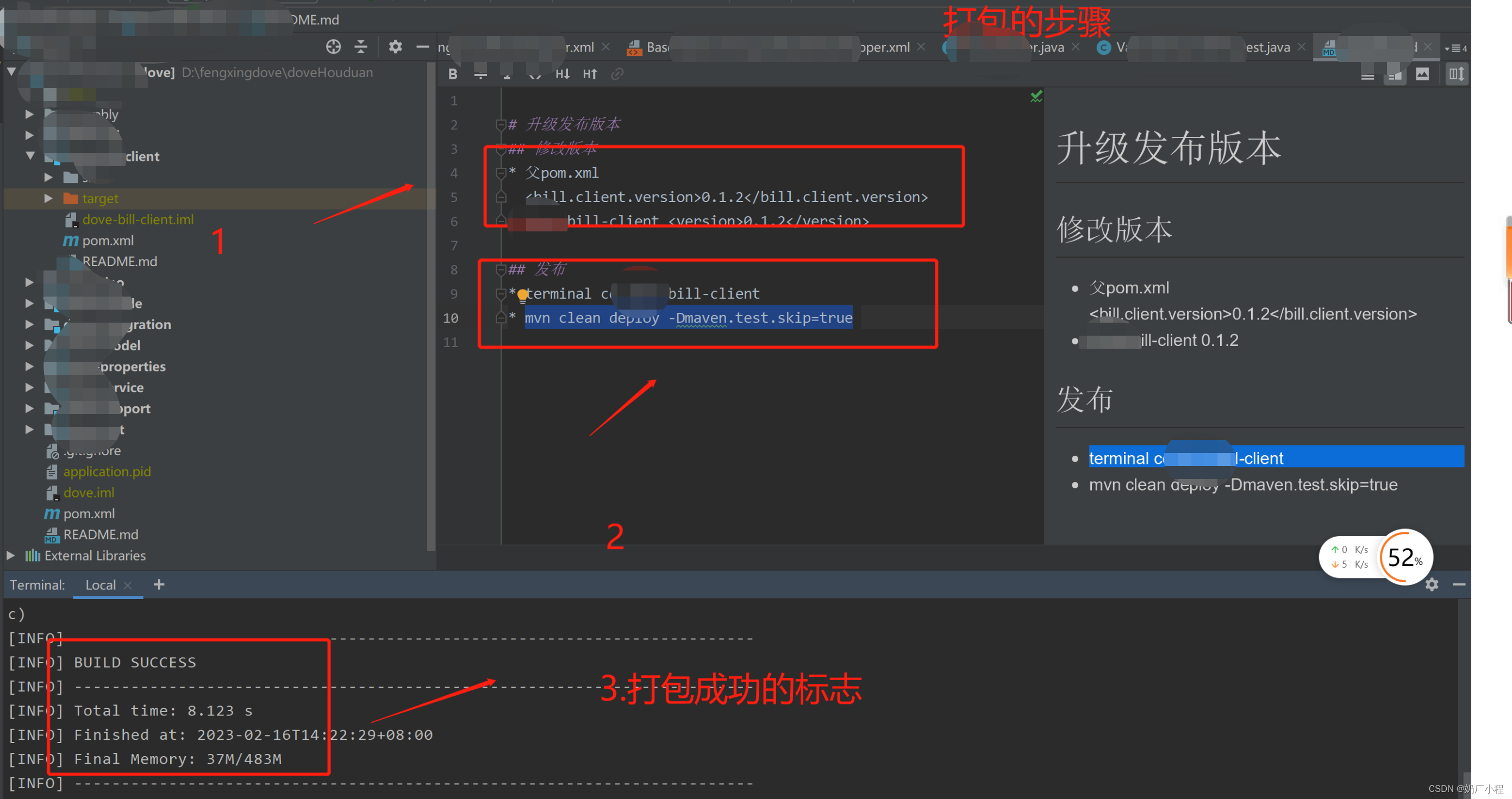
目录 前言 一、client如何打包升级? 二、使用步骤 1.先进行改版本 2.执行打包升级命令 总结 前言 本文章主要记录一下,日常开发中,常需要进行打包升级的步骤。 一、client如何打包升级? # 升级发布版本 ## 修改版本 * 父p…...

Blazor_WASM之3:项目结构
Blazor_WASM之3:项目结构 Blazor WebAssembly项目模板可选两种,Blazor WebAssemblyAPP及Blazor WebAssemblyAPP-Empty 如果使用Blazor WebAssemblyAPP模板,则应用将填充以下内容: 一个 FetchData 组件的演示代码,该…...

OperWrt 包管理系统02
文章目录 OperWrt 包管理系统OPKG简介OPKG的工作原理OPKG命令介绍软件包的更新、安装、卸载和升级等功能软件包的信息查询OPKG配置文件说明OPKG包结构(.ipk)OPKG演示案例OperWrt 包管理系统 OPKG简介 OPKG(Open/OpenWrt Package)是一个轻量快速的软件包管理系统,是 IPKG…...
人人都学会APP开发 提高就业竞争力 简单实用APP应用 安卓浏览器APP 企业内部通用APP制作 制造业通用APP
安卓从2009年开始流程于手机、平板,已经是不争的非常强大生产力工具,更为社会创造非常高的价值,现在已经是202X年,已经十几年的发展,安卓平台已经无所不在。因此建议人人都学学APP制作,简易入门,…...

【自然语言处理】从词袋模型到Transformer家族的变迁之路
从词袋模型到Transformer家族的变迁之路模型名称年份描述Bag of Words1954即 BOW 模型,计算文档中每个单词出现的次数,并将它们用作特征。TF-IDF1972对 BOW 进行修正,使得稀有词得分高,常见词得分低。Word2Vec2013每个词都映射到一…...
LIME: Low-light Image Enhancement viaIllumination Map Estimation
Abstract当人们在低光条件下拍摄图像时,图像通常会受到低能见度的影响。除了降低图像的视觉美感外,这种不良的质量还可能显著降低许多主要为高质量输入而设计的计算机视觉和多媒体算法的性能。在本文中,我们提出了一种简单而有效的微光图像增…...

源码指标编写1000问4
4.问: 哪位老师把他改成分析家的,组合公式:猎庄敢死队别样红(凤翔) {猎庄敢死队} rsv:(c-llv(l,9))/(hhv(h,9)-llv(l,9))100; stickline(1,50,50,1,0),pointdot,Linethick2,colorff00; k:sma(rsv,3,1); d:sma(k,3,1); rsv1:(hhv(h,9.8)-c)/(hhv(h,9.8)-llv(l,9.8))1…...

Golang中GC和三色屏障机制【Golang面试必考】
文章目录Go v1.3 标记—清楚(mark and sweep)方法Go V1.5 三色标记法三色标记过程无STW的问题强弱三色不变式插入写屏障Go V1.8的三色标记法混合写屏障机制混合写屏障场景场景1:对象被一个堆对象删除引用,成为栈对象的下游场景2:对象被一个栈对象删除引用࿰…...
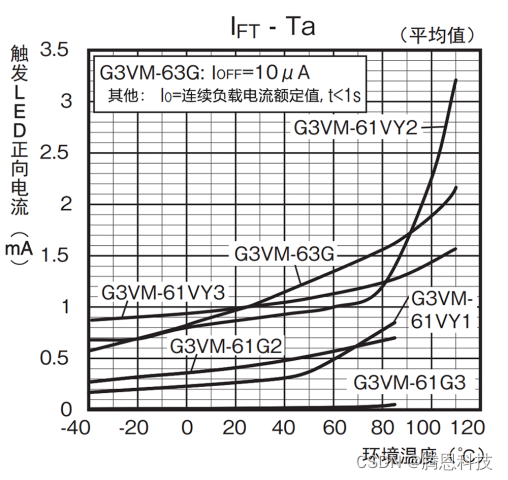
MOS FET继电器(无机械触点继电器)设计输入侧电源时的电流值概念
设计输入侧电源时的问题 机械式继电器、MOS FET继电器分别具有不同的特长。基于对MOS FET继电器所具小型及长寿命、静音动作等优势的需求,目前已经出现了所用机械式继电器向MOS FET继电器转化的趋势。 但是,由于机械式继电器与MOS FET继电器在产品结构…...

5. 驱动开发
文章目录一、驱动开发1.1 前言1.2 何谓驱动框架1.3 内核驱动框架中LED的基本情况1.3.1 相关文件1.3.2 九鼎移植的内核中led驱动1.3.3 案例分析驱动框架的使用1.3.4 典型的驱动开发行业现状1.4 初步分析led驱动框架源码1.4.1 涉及到的文件1.4.2 subsys_initcall1.4.3 led_class_…...

模板方法模式详解
模板方法模式(行为模式) 1. 模板方法模式介绍 父类定义算法骨架,细节的具体实现延迟到子类子类只是定义某些自己的个性化处理,但不改变执行顺序 2. 好处 减少代码冗余,共性抽取后算法流程更加清晰与规范降低流程性…...

关于 Lightweight process container,ChatGPT的答案
晓楚 Can you give me a list of process container? As an AI language model, I can provide you with a list of popular process containers, which are as follows: Docker Kubernetes Apache Mesos LXC OpenVZ systemd-nspawn rkt (Rocket) Linux Containers (LXC) Ga…...

机器学习和深度学习的综述
机器学习和深度学习的综述 1.1.1人工智能、机器学习、深度学习的关系 人工智能(Artificial Intelligence,AI)是最宽泛的概念,是研发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。由于这个定义…...

Synopsys Sentaurus TCAD系列教程之--Sprocess(SmallMOS_2D3D) 解析
SmallMOS_2D3D解析 #header## STI depth set sti_depth 0.15 ## Half STI width set sti_width sti_width ## Half gate length set gate_len <lg/2> ## SD length (from center) set sd_len [expr $gate_len0.05]#endheader## X lines line x location 0.0 spacing 0.…...
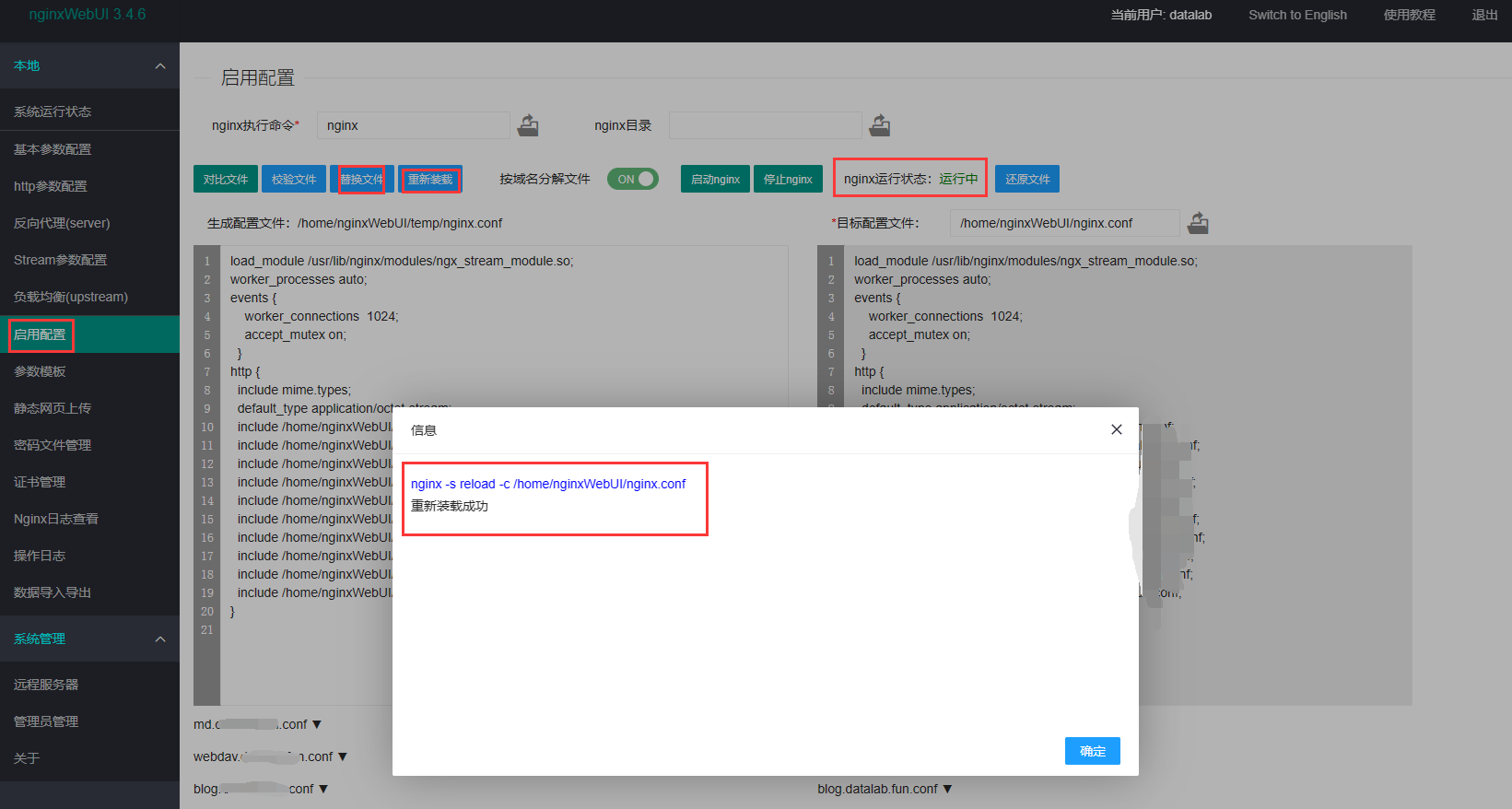
好使!NAS中傻瓜式配置反向代理及SSL证书,提升网络安全性!
对于有NAS或者有个人主机的朋友来说,将机器映射到外网是基本操作。 但是一般来说,能直接从外网访问的往往仅有80和443端口。事实上,运营商一般把家庭宽带的这两个端口都封了,所以如果我们想要从外网访问自己家中机器部署的服务&a…...

数据结构队列-先进先出
一,概述 队列这个概念非常好理解。你可以把它想象成排队买票,先来的先买,后来的人只能站末尾,不允许插队。先进者先出,这就是典型的“队列”。 二,顺序队列和链式队列 队列和栈一样,也是一种…...

CentOS 7使用TiUP部署TiDB
本文主要是根据官方文档指导,结合实际主机情况,在Cent OS7上使用TiUP在线部署TiDB。 环境说明 类型操作系统版本配置中控机Deepin 20.34核CPU6G内存40G硬盘TiDB部署机Cent OS 7.38核CPU48G内存100硬盘网络情况中控机与外网相连,中控机与部署…...
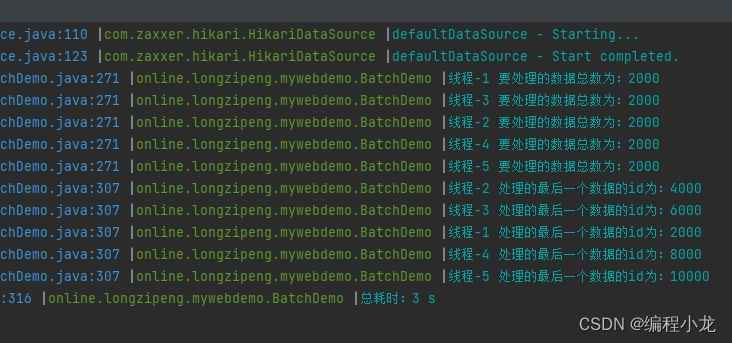
java单元测试批处理数据模板【亿点点日志配合分页以及多线程处理】
文章目录引入相关资料环境准备分页查询处理,减少单次批量处理的数据量级补充亿点点日志,更易观察多线程优化查询_切数据版多线程_每个线程都分页处理引入 都说后端开发能顶半个运维,我们经常需要对大量输出进行需求调整,很多时候…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
