LeetCode-279. 完全平方数【广度优先搜索 数学 动态规划】
LeetCode-279. 完全平方数【广度优先搜索 数学 动态规划】
- 题目描述:
- 解题思路一:Python 动态规划五部曲(完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?)
- 解题思路二:0
- 解题思路三:0
题目描述:
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
解题思路一:Python 动态规划五部曲(完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?)
-
确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j] -
确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
- dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?
看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, …),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。
非0下标的dp[j]应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
- 确定遍历顺序
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
在动态规划:322. 零钱兑换 (opens new window)中我们就深入探讨了这个问题,本题也是一样的,是求最小数!
所以本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
- 举例推导dp数组
已输入n为5例,dp状态图如下:

class Solution:def numSquares(self, n: int) -> int:dp = [float('inf')] * (n + 1) # return dp[n]dp[0] = 0for i in range(n+1): # 注意需要dp[n],那么这里需要n+1j = 1while j ** 2 <= i:dp[i] = min(dp[i], dp[i - j ** 2] + 1)j += 1return dp[n]
时间复杂度:O(n)
空间复杂度:O(n)
解题思路二:0
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)
相关文章:

LeetCode-279. 完全平方数【广度优先搜索 数学 动态规划】
LeetCode-279. 完全平方数【广度优先搜索 数学 动态规划】 题目描述:解题思路一:Python 动态规划五部曲(完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品…...
rust项目组织结构和集成测试举例
概述 在学习rust的过程中,当项目结构略微复杂的时候,写集成测试的时候发现总是不能引用项目中的代码,导致编写测试用例失败。查阅了教程,一般举例都很简单。查阅了谷歌和百度以及ai,也没有找到满意的答案。这里记录一…...

软件文档交付清单(直接套用合集)
软件文档交付清单是指在软件开发项目完成后,开发团队需要准备的一份详细清单,用于确保交付的软件产品符合客户需求并达到预期的质量标准。以下是软件文档交付清单中可能包含的一些关键要素 软件开发文档:这包括需求文档、设计文档、测试文档等…...
ModuleNotFoundError: No module named ‘ultralytics.utils‘
项目场景he 问题描述 提示:这里简述项目相关背景: model YOLO(modelr./yolov8m-cls.pt) 加载预训练模型时报错。 ModuleNotFoundError: No module named ultralytics.utils warning: bug: 原因分析: 很可能是提前下载的预训练模型出了…...

2024智能计算、大数据应用与信息科学国际会议(ICBDAIS2024)
2024智能计算、大数据应用与信息科学国际会议(ICBDAIS2024) 会议简介 智能计算、大数据应用与信息科学之间存在相互依存、相互促进的关系。智能计算和大数据应用的发展离不开信息科学的支持和推动,而信息科学的发展又需要智能计算和大数据应用的不断拓展和应用。智…...
秋招复习笔记——八股文部分:操作系统
笔试得刷算法题,那面试就离不开八股文,所以特地对着小林coding的图解八股文系列记一下笔记。 这一篇笔记是图解系统的内容。 硬件结构 CPU执行程序 计算机基本结构为 5 个部分,分别是运算器、控制器、存储器、输入设备、输出设备…...

每日一题:C语言经典例题之杨辉三角
题目描述 输出杨辉三角形。 输入 第一行输入一个整数 n (1<n<10)。 输出 输出杨辉三角形的前n行,每个数字占8格左对齐。 样例输入 4 样例输出 1 1 1 1 2 1 1 3 3 1 代码: #inc…...

1. TypeScript: JavaScript 的超集,为大型应用而生
引言 在现代的前端开发领域,JavaScript 无疑是一门极其流行的语言。然而,随着前端项目的日益复杂,JavaScript 本身的一些特性使得维护和扩展大型代码库变得困难。这就是 TypeScript 应运而生的背景。TypeScript 是一种由微软开发的开源语言&…...
vex-table—— 获取插入或修改数据后的tableData
例子来自vxe-table。在开发过程中发现新增数据后,输出this.tableData,发现数据并没有被修改 想要获取更新的数据方式为 mounted () {const $table this.$refs.xTableconsole.log("🚀 ~ mounted ~ $table:", $table.tableData)},...

通俗易懂地解释Go语言不同版本中垃圾回收机制的演进过程
完整课程请点击以下链接 Go 语言项目开发实战_Go_实战_项目开发_孔令飞_Commit 规范_最佳实践_企业应用代码-极客时间 Go 1.3时代 - 标记清除算法 这就像一个人要打扫房间,首先需要暂停其他活动。然后开始查看房间里的每件物品,对于自己仍需要使用的物品做上记号。查看完毕后…...
shamrockcms代码审计-啥也没有
shamrockcms 环境搭建 使用阿里源,创建数据库,运行shamrockcms.sql文件,将configure.properties中的jdbc修改为自己本地或者其他ip数据库连接,并且将ueditor.config.json中的master修改为localhost或者其他自己设置的ip 危险组件…...
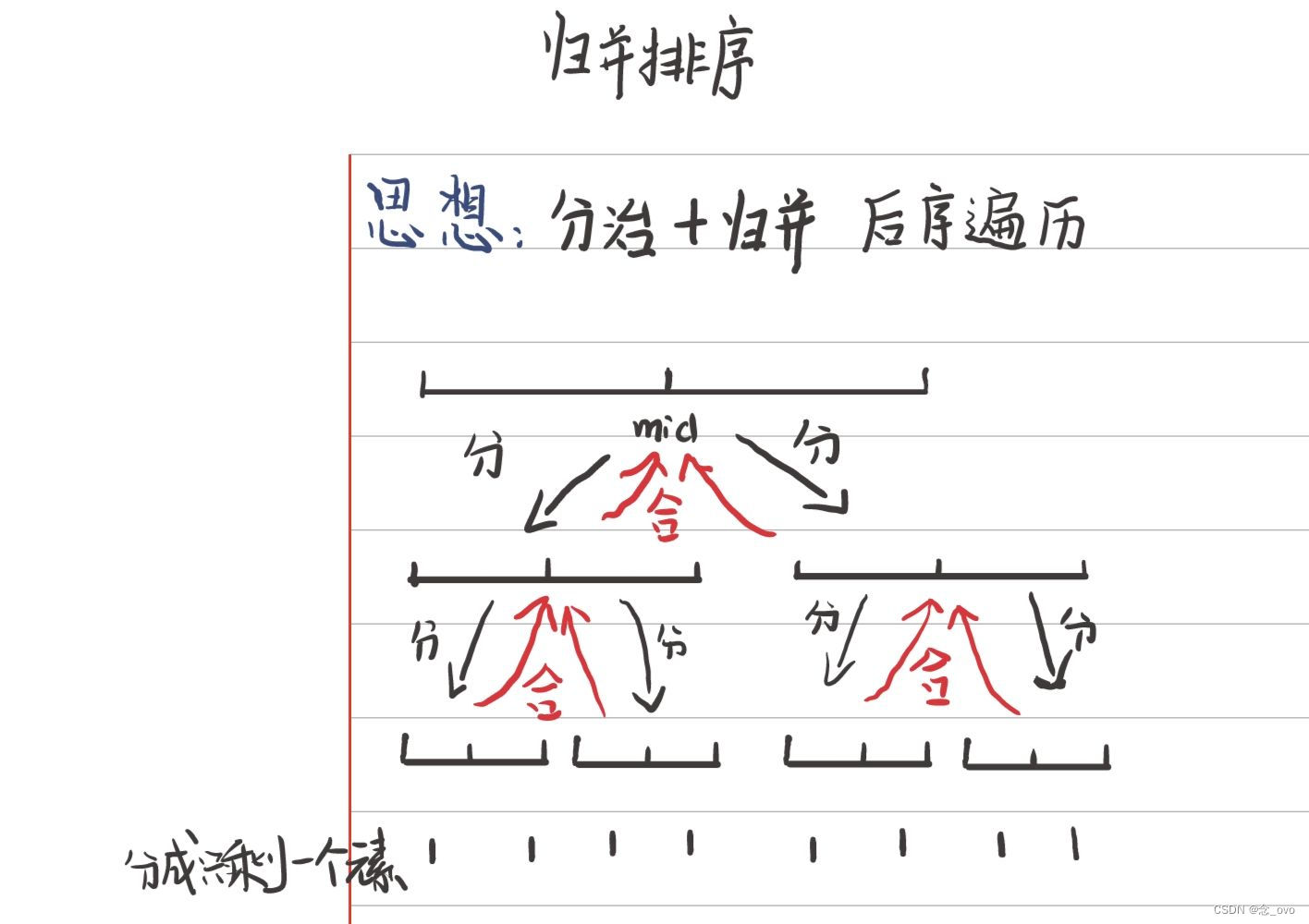
【C++】排序算法 --快速排序与归并排序
目录 颜色分类(数组分三块思想)快速排序归并排序 颜色分类(数组分三块思想) 给定⼀个包含红⾊、⽩⾊和蓝⾊、共 n 个元素的数组 nums ,原地对它们进⾏排序,使得相同颜⾊ 的元素相邻,并按照红⾊、…...
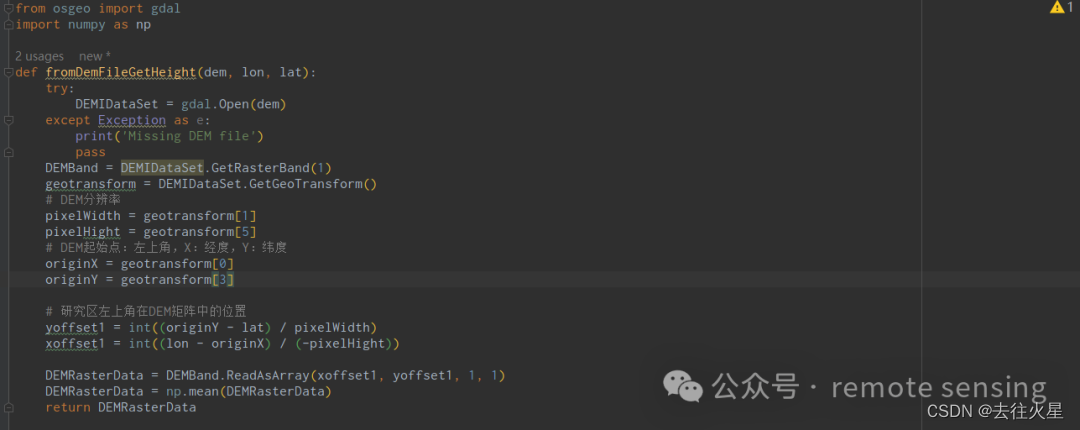
(Python)根据经纬度从数字高程模型(DEM)文件获取高度
基本介绍 在地理信息系统(GIS)和遥感中,数字高程模型(Digital Elevation Model,简称DEM)是一种表示 地表或地形高程信息的重要数据。DEM数据通常以栅格(raster)形式存在࿰…...

【WPF应用41】WPF中的Expander控件详解
Windows Presentation Foundation(WPF)中的Expander控件是一个用于显示详细信息的交互式UI元素。它允许用户通过点击标题来展开或折叠内容区域。Expander控件通常用于在界面上组织内容,提供一种可见/隐藏的功能,以帮助用户专注于当…...

golang变量初始化顺序
顺序: 1.引用的包 2.全局变量 3.init()函数 4.main()函数 package pkgimport "fmt"func init() {fmt.Println("pkg init") }package mainimport ("fmt"_ "gg/pkg" )var v val()func val() int {fmt.Println("func()…...

魔众 文库配置异步转换
同步转换 系统默认使用同步转换,即用户上传文档提交接口瞬间,系统会立即进行转换。 同步转换容易造成页面卡顿,转换时间超长的情况下,系统接口会超时。 异步转换 系统支持异步转换,即用户上传文档提交接口瞬间&…...
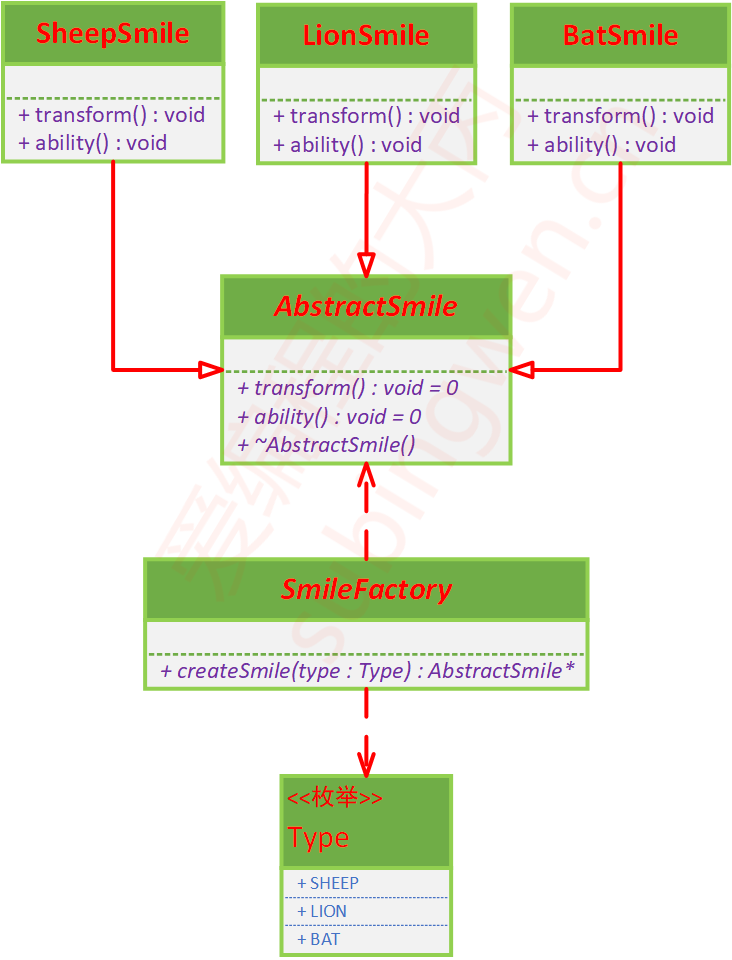
创建型模式--2.简单工厂模式【人造恶魔果实工厂1】
1. 工厂模式的特点 在海贼王中,作为原王下七武海之一的多弗朗明哥,可以说是新世界最大的流氓头子,拥有无上的权利和无尽的财富。他既是德雷斯罗萨国王又是地下世界的中介,控制着世界各地的诸多产业,人造恶魔果实工厂就…...

一些考研经验
前言 考研结束已有半个月,之前一直想写经验贴,奈何感觉自己本身就比较菜,考了两年才堪堪上岸,所以有些犹豫,拖拖沓沓到现在,思虑再三最终决定把自己对于考研的一些拙见记录一下,供各位参考。 …...
StockTrading AI小模型股票自动交易系统 转载
Stock-Trading StockTrading AI小模型股票自动交易系统 项目文档 Stock-Trading 语雀 项目展示 功能介绍 对接证券平台,实现股票自动化交易使用QuartZ定时任务调度,每日自动更新数据使用DL4J框架实现LSTM模型指导股票买入,采用T1短线交易策…...

01背包问题合集 蓝桥OJ
一、蓝桥OJ 1174小明的背包1 模板题 思路: 用二维数组dp判断最大价值,i表示物品数量,j表示物品体积,如果 j > V 则无需继续, j > w 物品还能再增加,同样价值也增加,否则继承之前的价值&am…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
