LeetCode 热题 100 题解(二):双指针部分(2)| 滑动窗口部分(1)
题目四:接雨水(No. 43)
题目链接:https://leetcode.cn/problems/trapping-rain-water/description/?envType=study-plan-v2&envId=top-100-liked
难度:困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
题解
首先来观察对于一个格子来说,它的容量是多少:

比如上图中的红色部分,它存储水的容量其实就是 左边的最大高度 和 右边的最大高度 的 最小值,减去这里的格子高度(案例中为 0),在上面的案例中,左边的最高高度为 2,右边的最高高度为 3。
所以本题的暴力解法就比较好想了,找到其左边最大高度,再找到其右边的最大高度,通过上面的规律进行运算。
class Solution {public int trap(int[] height) {int res = 0;for (int i = 1; i < height.length; i++) {int left = i - 1;int right = i + 1;int maxLeft = 0;int maxRight = 0;while (left >= 0) { // 去左边寻找最大的maxLeft = Math.max(maxLeft, height[left--]);}while (right < height.length) { // 去右边寻找最大的maxRight = Math.max(maxRight, height[right++]);}int temp = Math.min(maxLeft, maxRight) - height[i]; // 执行运算逻辑res += temp > 0 ? temp : 0;}return res;}
}
这个方法的时间复杂度无疑是非常高的,因为每遍历到一个节点的时候都需要遍历整张表,接下来考虑如何对上面的方法进行优化。
首先来看左边的最大值,考虑一下,我们真的有必要每次去遍历来求得最大值吗?
可以将之前遍历过的节点的最大值保存下来,比如说这么一个高度数组 4,2,0,3,2,5 ,我们从第二个数字开始遍历,当执行完这个数字的逻辑之后,就可以拿它和之前的最大高度作比较,用作下一个节点的左边最大高度,这样不断更新就能保证每次求得的都是准确的。
class Solution {public int trap(int[] height) {int res = 0;int maxLeft = height[0];for (int i = 1; i < height.length; i++) {int left = i - 1;int right = i + 1;int maxRight = 0;while (right < height.length) { // 找到右边最大高度maxRight = Math.max(maxRight, height[right++]);}int temp = Math.min(maxLeft, maxRight) - height[i];res += temp > 0 ? temp : 0;maxLeft = Math.max(height[i], maxLeft); // 维护一个更新的 maxLeft}return res;}
}
既然对左边可以进行优化,那对右边是否可以优化呢?
因为是从前向后遍历的,所以右边肯定不可能像左边这样简单的更新;所以可以考虑提前处理,如果从后向前遍历的话,就可以类似左边那样求出 每个节点 的右最大值,所以可以在进入循环之前,先遍历一次高度数组,求出一个存储着每个节点右最大值的数组。
class Solution {public int trap(int[] height) {int res = 0;int maxLeft = height[0];int k = 2;int[] maxRight = new int[height.length];int m = height[maxRight.length - 1];for (int j = maxRight.length - 2; j >= 0; j--) { // 从后向前遍历,维护一个存储每个节点最大值的数组maxRight[j] = m;m = Math.max(m, height[j]);}for (int i = 1; i < height.length; i++) {int temp = Math.min(maxLeft, maxRight[i]) - height[i]; // 使用数组中的值res += temp > 0 ? temp : 0;maxLeft = Math.max(height[i], maxLeft);}return res;}
}
题目一:无重复字符的最长字串(No. 3)
题目链接:https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/?envType=study-plan-v2&envId=top-100-liked
题目难度:中等
给定一个字符串 s ,请你找出其中不含有重复字符的 最长
子串
的长度。
示例 1:
输入:s = "abcabcbb"
输出:3
解释: 因为无重复字符的最长子串是"abc",所以其长度为 3。
示例 2:
输入:s = "bbbbb"
输出:1
解释:因为无重复字符的最长子串是"b",所以其长度为 1。
示例 3:
输入:s = "pwwkew"
输出:3
解释:因为无重复字符的最长子串是"wke",所以其长度为 3。请注意,你的答案必须是子串的长度,"pwke" 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
题解
首先来看第一种方法,提到最长子串,想到的第一个方法就是动态规划。
先来尝试找一下状态,题目中问的是没有重复字符的最长的子串,可以将某个节点的状态定义为:以这个节点为结尾的,不含有重复字符的字串的最大长度,这种方式在处理子串的问题中非常常见。
再来思考这个状态应该如何转移。对于一个节点其实有这些选择
- 从这个节点开始(重新开始)
- 接续前面的子串
本题接续前面子串的时候要考虑不能含有重复的元素,所以并不像之前的题目那样就简单的做一个加一,但总而言之状态是可以转移的,那就来尝试一下。
先来确定 dp 数组,根据上面的推理,dp 数组只需要一维就即可, dp[i] 的含义为以 s.charAt(i) 为结尾的,不含有重复子串的最大长度。
然后就是确定状态转移方程了,对于一个下标为 x 的节点,它所代表的子串就是从 x - dp[i] 到 x 这个范围内内容;比如我们现在遍历到了下标为 x + 1 的节点,如果想要接续上前面的内容,就需要上面的范围中不含有 s.charAt(x + 1) 这个字符,此时需要通过遍历来确定是否有这个字符。
如果没有发现,那 dp[i] = dp[i - 1] + 1
如果发现了重复的字符串,比如下面的情况
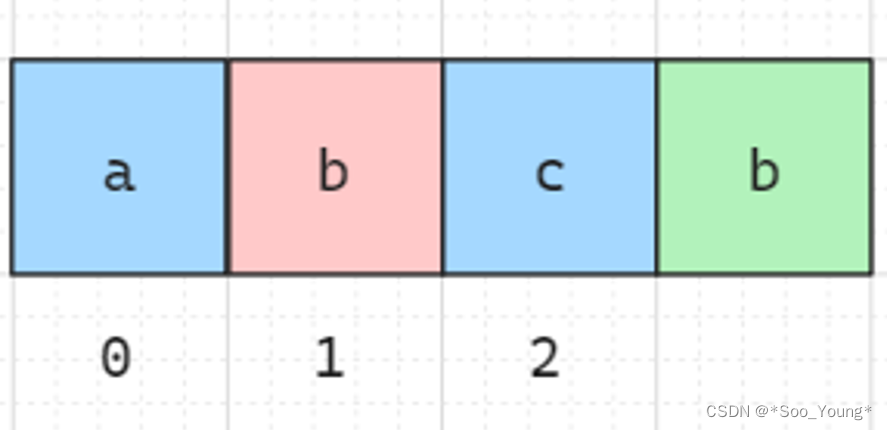
此时要求得的是绿色的 b 的值,前一个节点最大子串的长度为 3,但当遍历到图中粉色的节点的时候发现了重复,此时 b 的长度应该为多少呢?是 2
画个图来更直观的了解一下:

当发现了相同的节点之后,这个值应该就是从被发现的位置索引 + 1 一直到新节点的长度
此时就确定了两种情况的递推公式,下面来讨论一下初始化
因为需要前一个节点的情况,所以 dp[0] 是要被初始化的,按照上面的含义,该位置应该被初始化为 1。
class Solution {public int lengthOfLongestSubstring(String s) {if (s.length() == 0) return 0;int[] dp = new int[s.length()];dp[0] = 1;int res = 1;for (int i = 1; i < s.length(); i++) {int field = dp[i - 1]; // 需要查询重复的范围char c = s.charAt(i);boolean findSame = false; // 是否找到了相同的节点while (field > 0) {int index = i - (field--);if (s.charAt(index) == c) { // 找到了相同的节点int m = i - index - 1 + 1;dp[i] = m;findSame = true;break;}}if (!findSame) dp[i] = dp[i - 1] + 1;res = Math.max(dp[i], res); // 动态更新 res}return res;}
}
接下来来看一下滑动窗口方案
所谓的滑动窗口其实就是用索引去限定一个范围,通过不断移动左范围和右范围的方式来调整窗口的范围,从而收集信息。
当滑动窗口的内容满足要求的时候就不断 移动右边界,来扩展滑动窗口的大小,如果发现不满足要求,也就是出现了重复的情况,就通过 收缩左边界 最终使得窗口内的元素始终满足要求,然后记录滑动窗口的长度。
滑动窗口方法的核心和上面的动态规划方法相同,都是通过遍历每个元素为 右节点 的情况,来不断更新最大值。
class Solution {char[] charArray;public int lengthOfLongestSubstring(String s) {if (s.length() == 0) return 0;charArray = s.toCharArray();int left = 0, right; // 左范围,右范围int res = 1;for (int i = 1; i < charArray.length; i++) {right = i;while (examine(left, right, charArray[i])) {left++;}res = Math.max(right - left + 1, res); // 更新结果}return res;}// 检测范围内是否有和此时右范围相同的元素public boolean examine(int left, int right, char c) {for (int i = left; i <= right - 1; i++) {if (charArray[i] == c) return true;}return false;}
}
相关文章:

LeetCode 热题 100 题解(二):双指针部分(2)| 滑动窗口部分(1)
题目四:接雨水(No. 43) 题目链接:https://leetcode.cn/problems/trapping-rain-water/description/?envTypestudy-plan-v2&envIdtop-100-liked 难度:困难 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图&am…...

常用的深度学习自动标注软件
0. 简介 自动标注软件是一个非常节省人力资源的操作,而随着深度学习的发展,这些自动化标定软件也越来越多。本文章将会着重介绍其中比较经典的自动标注软件 1. AutoLabelImg AutoLabelImg 除了labelimg的初始功能外,额外包含十多种辅助标注…...

选择程序员是为什么?
本章节是关于为什么会选择一名程序员的经验分享 首先,我为什么会选择这个方向,可能是因为钱多,学东西不就是为了赚钱嘛?这是一点,不过最让我接收这个行业的是好奇世界的新大陆,可以简单的说就是,…...
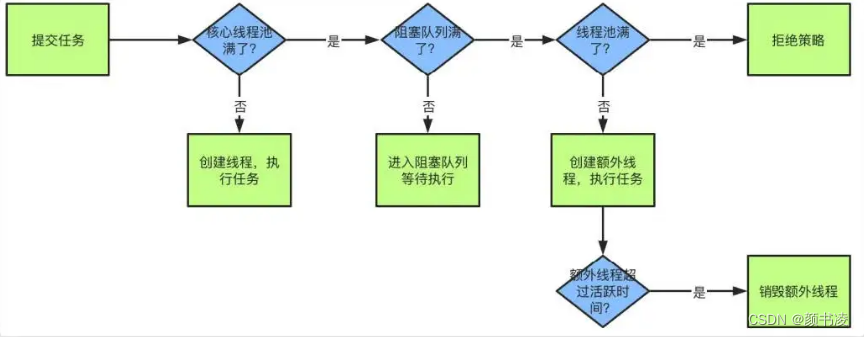
线程池参数如何设置
线程池参数设置 hello丫,各位小伙伴们,好久不见了! 下面,我们先来复习一下线程池的参数 1、线程池参数有哪些? corePoolSize(核心线程数):线程池中的常驻核心线程数。即使这些线程…...
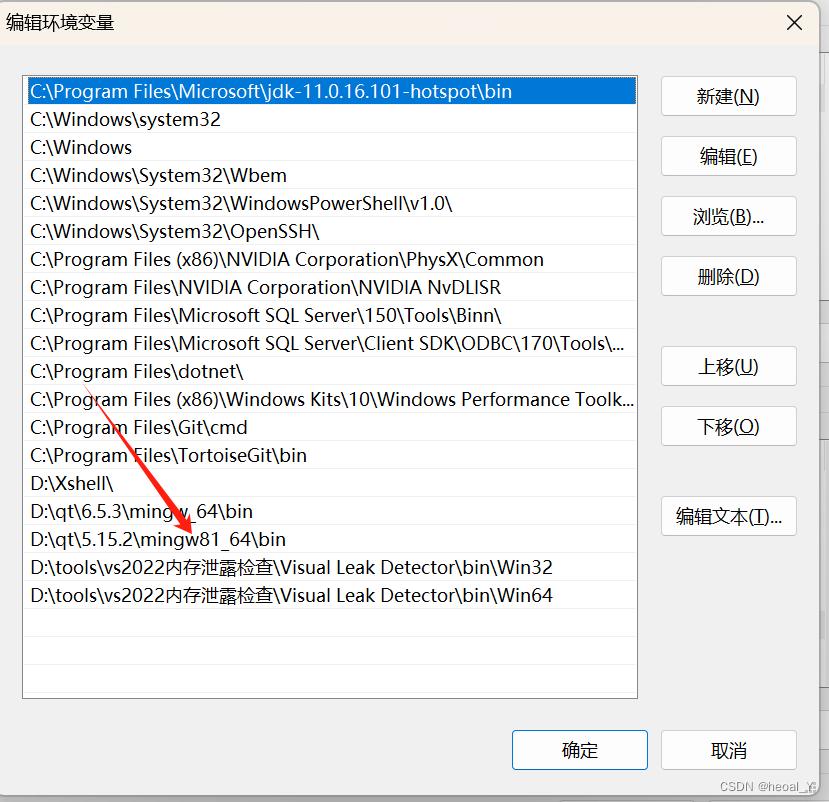
qt环境搭建-镜像源安装Qt Creator(5.15.2)以及配置环境变量
前言: 版本:5.15.2 镜像源:ustc与清华 纯小白,找了半天的镜像源安装qtcreator,搞了半天结果安装的是最新的,太新的对小白很不友好,bug比较多,支持的系统也不全,口碑不…...
SQL Server详细安装使用教程
1.安装环境 现阶段基本不用SQL Server数据库了,看到有这样的分析话题,就把多年前的存货发一下,大家也可以讨论看看,思路上希望还有价值。 SQL Server 2008 R2有32位版本和64位版本,32位版本可以安装在Windows XP及以上…...

深度解读C++17中的std::string_view:解锁字符串处理的新境界
深入研究C17中的std::string_view:解锁字符串处理的新境界 一、简介二、std::string_view的基础知识2.1、构造函数2.2、成员函数 三、std::string_view为什么性能高?四、std::string_view的使用陷阱五、std::string_view源码解析六、总结 一、简介 C中有…...

汇编基础-----常见命令基本使用
汇编基础-----常见命令基本使用 MOV:将数据从一个位置复制到另一个位置。 MOV destination, source例如: MOV RAX, RBX ; 将RBX寄存器中的值复制到RAX寄存器中ADD/SUB:将两个操作数相加或相减。 ADD destination, source SUB destinatio…...
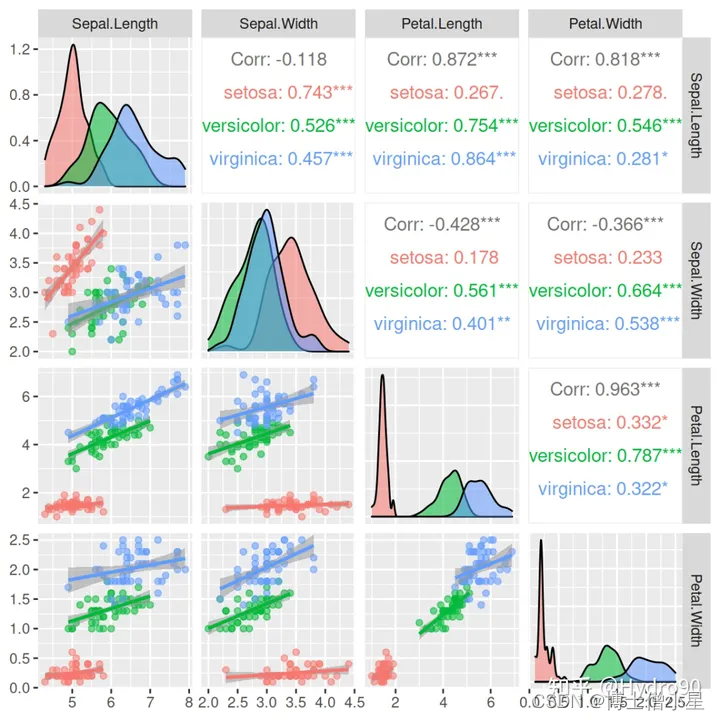
科研学习|可视化——相关性结果的可视化
一、相关性分析介绍 相关性分析是指研究两种或者两种以上的变量之间相关关系的统计分析方法,一般分析步骤为: 1)判断变量间是否存在关联;2)分析关联关系(线性/非线性)、关联方向(正相…...
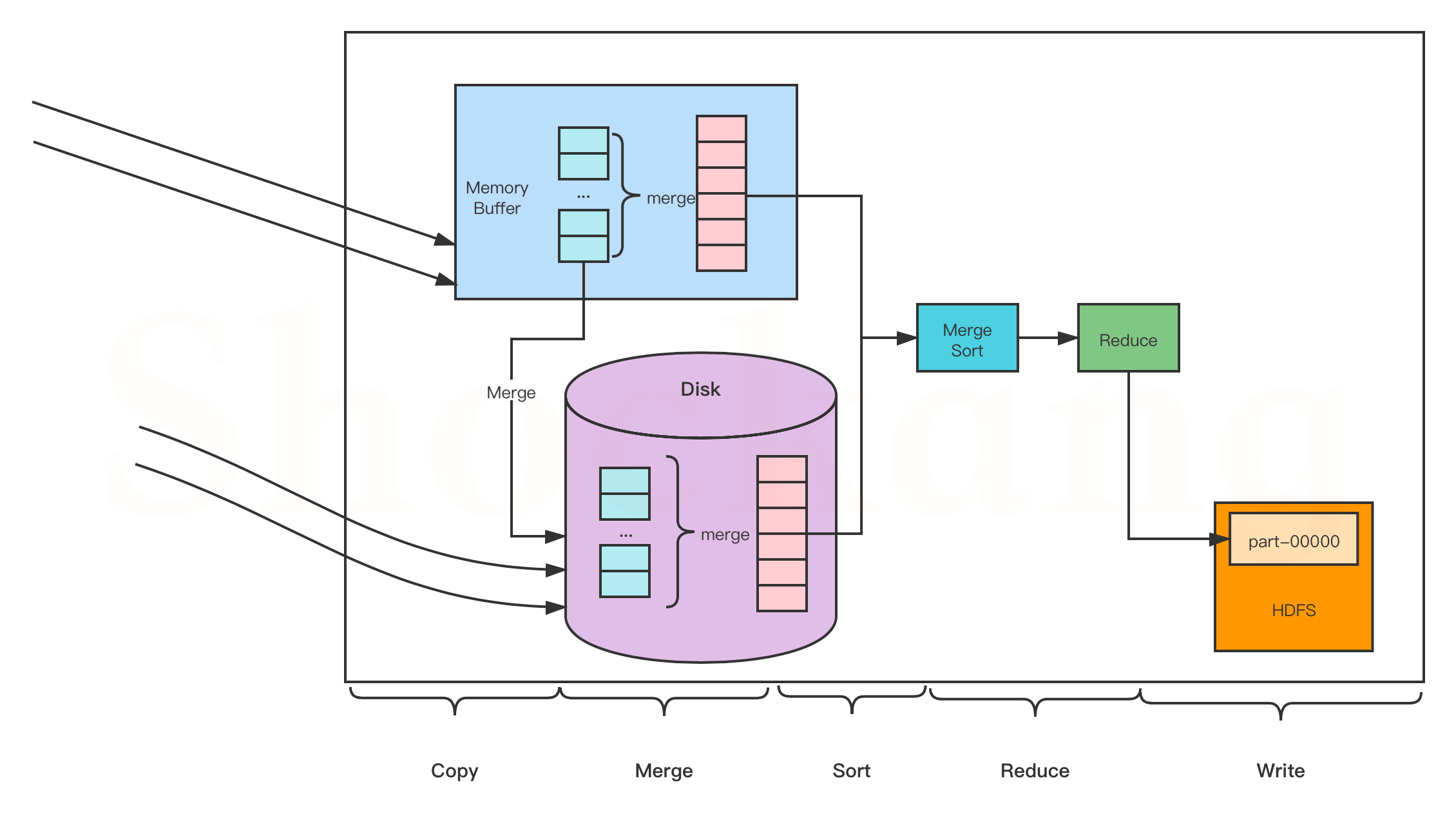
MapReduce过程解析
一、Map过程解析 Read阶段:MapTask通过用户编写的RecordReader,从输入的InputSplit中解析出一个个key/value。Map阶段:将解析出的key/value交给用户编写的Map()函数处理,并产生一系列的key/value。Collect阶段:在用户编…...

速看!这8道嵌入式面试题你都会吗?
大家好,我是知微! 正逢求职季,分享一些嵌入式面试当中经常会遇到的题目,希望这些干货对小伙伴们面试有用哦! 1、介绍一下static关键字的作用 在C语言中,static 关键字有几种不同的作用,根据其…...

基于SSM的电影网站(有报告)。Javaee项目。ssm项目。
演示视频: 基于SSM的电影网站(有报告)。Javaee项目。ssm项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring SpringMv…...
SOCKS代理是如何提高网络性能和兼容性的?
SOCKS代理作为一种网络协议中间件,不仅在提升网络隐私和安全性方面发挥着重要作用,也在提高网络性能和兼容性方面有着不容忽视的影响🚀。本文将深入探讨SOCKS代理如何通过减少网络延迟🚀、优化数据传输🔄、提高跨平台兼…...
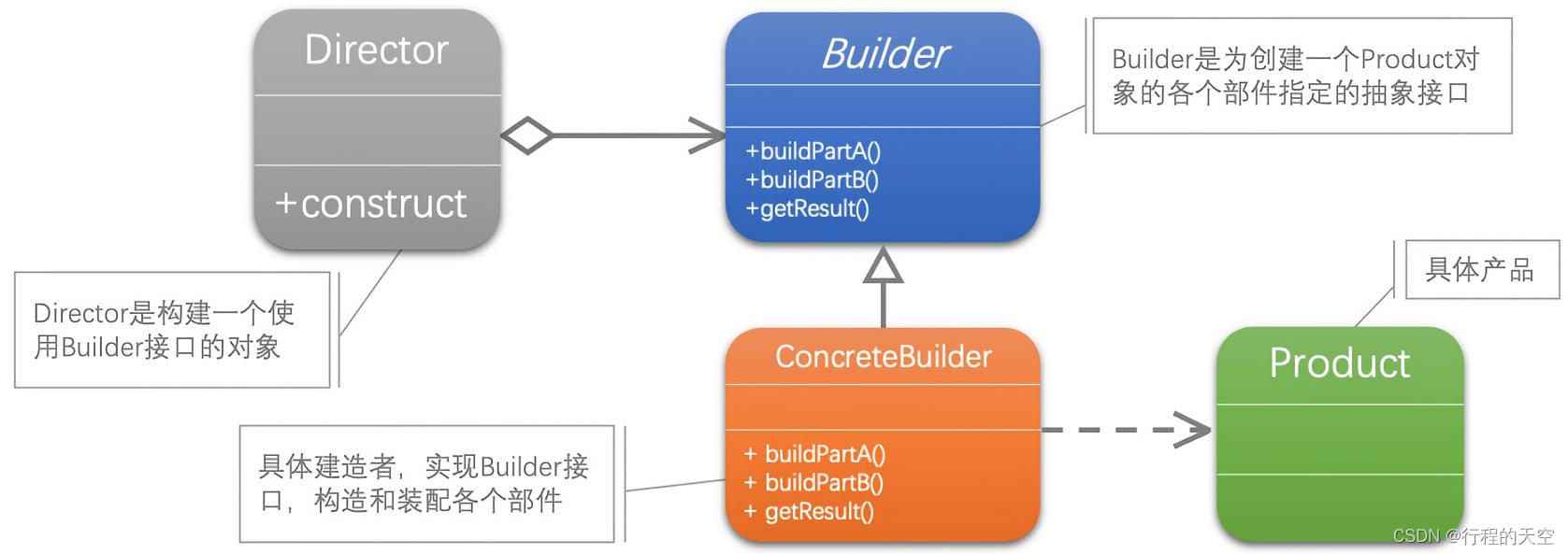
好菜每回味道不同--建造者模式
1.1 炒菜没放盐 中餐,老板需要每次炒菜,每次炒出来的味道都有可能不同。麦当劳、肯德基这些不过百年的洋快餐却能在有千年饮食文化的中国发展的那么好呢?是因为你不管何时何地在哪里吃味道都一样,而鱼香肉丝在我们中餐却可以吃出上…...

RuoYi-Cloud下载与运行
一、源码下载 若依官网:RuoYi 若依官方网站 鼠标放到"源码地址"上,点击"RuoYi-Cloud 微服务版"。 跳转至Gitee页面,点击"克隆/下载",复制HTTPS链接即可。 源码地址为:https://gitee.com/y_project/RuoYi-Cloud.git 点击复制 打开IDEA,选…...

Vue2.x计算属性
1.计算属性 在Vue 插值表达式内实现一些操作其实非常便利,但如果表达式的逻辑过于复杂,会让插值过于臃肿且难以维护。这时可以考虑使用Vue的计算属性 1.1 不使用计算属性的例子 <!DOCTYPE html> <html><head><meta charset"…...
自动引入组件和自动生成路由的方法介绍)
Vue中使用require.context()自动引入组件和自动生成路由的方法介绍
目录 一、自动引入组件 1、语法 2、使用 2.1、在compoents文件下随便创建index.js文件 2.2、mian.js引入该js 二、自动生成路由 1、示例: 2、使用 2.1、在router文件下随便创建autoRouter.js文件 2.2、在router文件下index.js文件中引入autoRouter.js文件…...
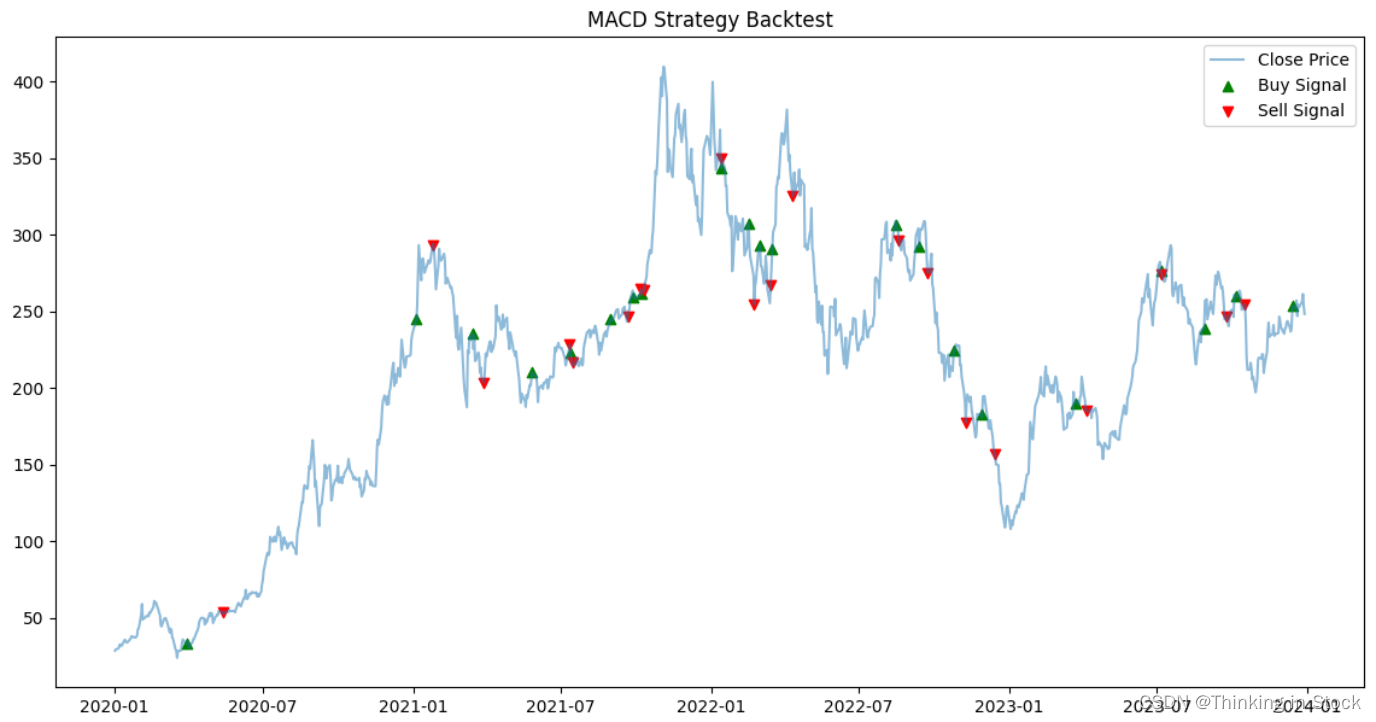
【炒股Zero To Hero】MACD金叉死叉到底是否有效,加上这个指标回报率增加197倍
移动平均收敛散度(MACD - Moving Average Convergence Divergence)是一种趋势跟踪动量指标,显示了证券价格的两个移动平均之间的关系。它用于识别趋势的方向和强度,属于技术分析中振荡器的一类。 MACD如何衡量股票及其趋势 有两…...

Linux网络名称空间和虚拟机有何区别
在Linux系统中,网络名称空间和虚拟机都是实现资源隔离和虚拟化的技术,但它们在设计理念、实现机制、资源消耗、使用场景等方面存在着显著的区别。本文旨在全方位、系统性地分析这两种技术的区别。🔍 1. 设计理念与实现机制 1.1. 网络名称空…...
【UE Niagara】蓝图获取粒子数据
目录 效果 步骤 一、创建粒子 二、创建蓝图接收Niagara参数 效果 步骤 一、创建粒子 1. 新建一个Niagara发射器,使用Empty模板,打开后先添加“Spawn Rate”模块,这里设置粒子生成速率为0.7 在“Initialize Particle”模块中设置粒子颜色…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
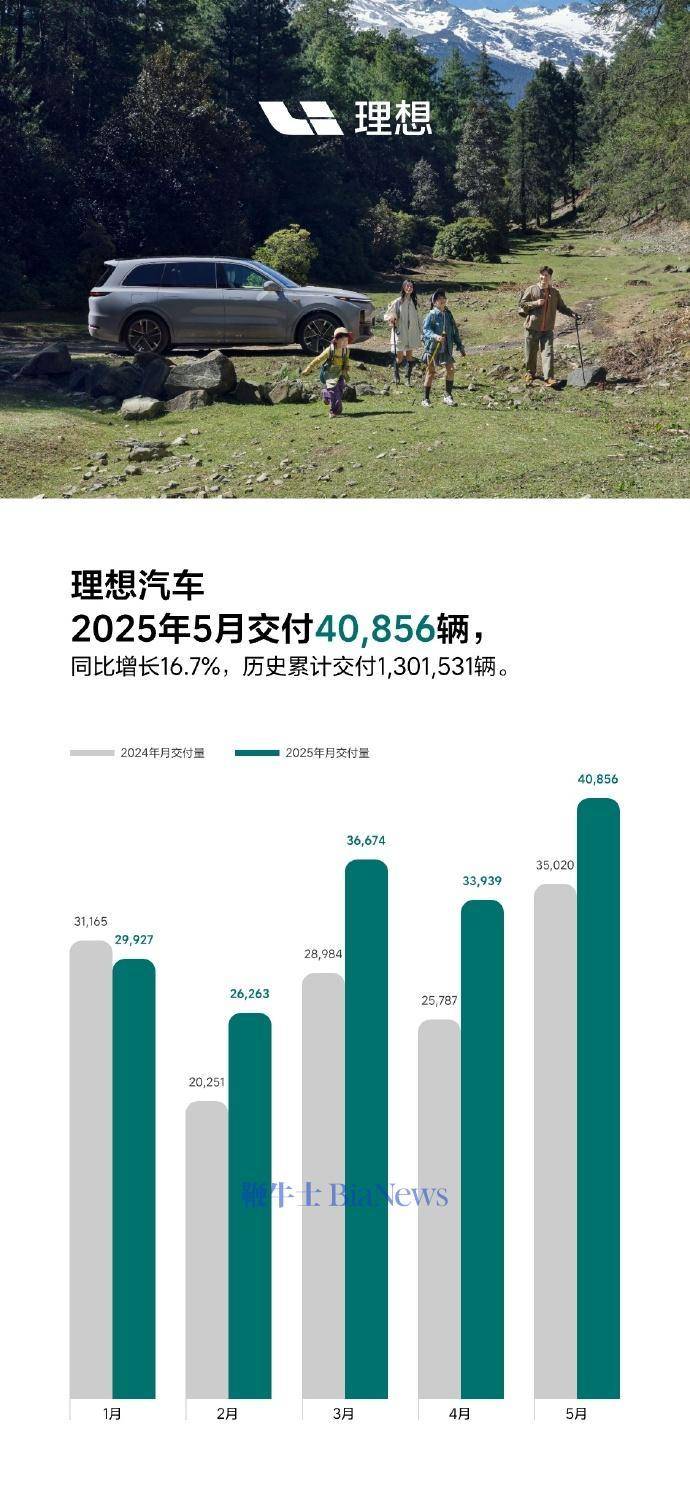
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
