cesium 调整3dtiles的位置 世界坐标下 相对坐标下 平移矩阵
cesium调整3dtiles的位置用到的是平移矩阵,原理是在世界坐标系中用偏移点减去原始点得到一个平移向量,再根据这个向量得到平移矩阵。
- 原始点:一般是模型的中心点位置,可通过模型的包围盒得到
- 偏移点:可分为两种情况,
- 直接给出世界坐标系中的一个位置,这两个点在世界坐标系中没有相对关系
- 给出模型的相对位置,比如说让模型沿x轴正方向偏10米,此时这个偏移点和模型就有相对关系,但是偏移点在世界坐标系中并没有描述,因此需要根据模型建立一个局部坐标系,将局部坐标系变换到世界坐标,求出偏移点在世界坐标系中的值。注意:到这一步情况就和1相同了,后面的转换也和1相同。
一、加载 3dtiles
tileset = new Cesium.Cesium3DTileset({url: '/data/tileset.json',maximumScreenSpaceError: 2, //最大的屏幕空间误差maximumNumberOfLoadedTiles: 1000, //最大加载瓦片个数dynamicScreenSpaceError: true,dynamicScreenSpaceErrorDensity: 0.00278,dynamicScreenSpaceErrorFactor: 4.0,dynamicScreenSpaceErrorHeightFalloff: 0.25,skipLevelOfDetail: true,baseScreenSpaceError: 1024,skipScreenSpaceErrorFactor: 16,skipLevels: 1,immediatelyLoadDesiredLevelOfDetail: false,loadSiblings: false,cullWithChildrenBounds: true,});viewer.scene.primitives.add(tileset);二、世界坐标系中的平移
tileset.readyPromise.then(function () {// 模型外包围盒,center:模型中心点,radius:包围盒半径let boundingSphere = tileset.boundingSphere;// 模型中心点let origin = boundingSphere.center;// 偏移后的位置,世界坐标系中的位置,比如从经纬度1的位置偏移到经纬度2的位置,并不知道1和2的相对关系let offset = Cesium.Cartesian3.fromDegrees(113.296969, 38.390417, 39.974122);// 计算世界坐标系下平移向量let translate = Cesium.Cartesian3.subtract(offset,origin,new Cesium.Cartesian3());tileset.modelMatrix = Cesium.Matrix4.fromTranslation(translate);});三、相对位置的平移
tileset.readyPromise.then(function () {// 模型外包围盒,center:模型中心点,radius:包围盒半径let boundingSphere = tileset.boundingSphere;// 模型中心点let origin = boundingSphere.center;// 获取到以模型中心为原点,Z轴垂直地表的局部坐标系,以矩阵表示,此矩阵为将局部坐标系变换到世界坐标系的变换矩阵let localMatrix = Cesium.Transforms.eastNorthUpToFixedFrame(origin);// 平移向量(tx,ty,tz) 此处表示沿着x轴平移10米,y轴和z轴不变let tempTranslation = new Cesium.Cartesian3(10, 0, 0);// 偏移后的位置,世界坐标系中的位置,即:局部坐标中(tx,ty,tz)在世界坐标系中位置let offset = Cesium.Matrix4.multiplyByPoint(localMatrix, tempTranslation, new Cesium.Cartesian3(0, 0, 0));// 计算世界坐标系下平移向量let translate = Cesium.Cartesian3.subtract(offset,origin,new Cesium.Cartesian3());tileset.modelMatrix = Cesium.Matrix4.fromTranslation(translate);});总结:两种情况的平移原理是一样的,都是在世界坐标系中 偏移点-原始点 得到平移向量,只是相对位置的平移多了局部坐标系到世界坐标系转换的过程。
相关文章:

cesium 调整3dtiles的位置 世界坐标下 相对坐标下 平移矩阵
cesium调整3dtiles的位置用到的是平移矩阵,原理是在世界坐标系中用偏移点减去原始点得到一个平移向量,再根据这个向量得到平移矩阵。 原始点:一般是模型的中心点位置,可通过模型的包围盒得到偏移点:可分为两种情况&…...

flutter跑通腾讯云直播Demo
运行示例 前提条件 要求java jdk 11版本 并且配置到了环境变量 重要 要求flutter 版本 2.8.0 并且配置到了环境变量 重要 要求dart-sdk版本2.15 并且配置到了环境变量 重要 您已 注册腾讯云 账号,并完成 实名认证。 申请 SDKAPPID 和 SECRETKEY 登录实时音视频控…...

飞机降落蓝桥杯[2023蓝桥省赛B组]
2023蓝桥省赛B组 B题 飞机降落 题解 标准深搜板子题,难度不大 #include<bits/stdc.h> using namespace std; #define MAX 10 struct node{int t,d,l;//t:飞机到达时间 d:飞机最大盘旋时间 l:飞机降落所需时间bool v;//标记此架飞机是否被搜索过 用于剪枝 };…...

如何动态渲染HTML内容?用v-html!
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

EFcore 6 连接oracle19 WinForm vs2022
用EFcore访问Oracle,终于不需要Oracle的什么安装包了,直接在VS2022中就可以轻松搞定。在csdn上看到一哥们的帖子,测试了一下,发现很方便。使用的场景是:VS2022中EFcore6。经过测试,同 Navicat Premium 16比…...
 Object Pascal 学习笔记---第9章第2节(finally代码块))
(delphi11最新学习资料) Object Pascal 学习笔记---第9章第2节(finally代码块)
9.2 finally 代码块 还有第四个用于异常处理的关键字,我已经提到过,但到目前为止还没有使用过,那就是 finally。finally块用于执行一些应始终执行的操作(通常是清理操作)。事实上,无论是否发生异常&…...
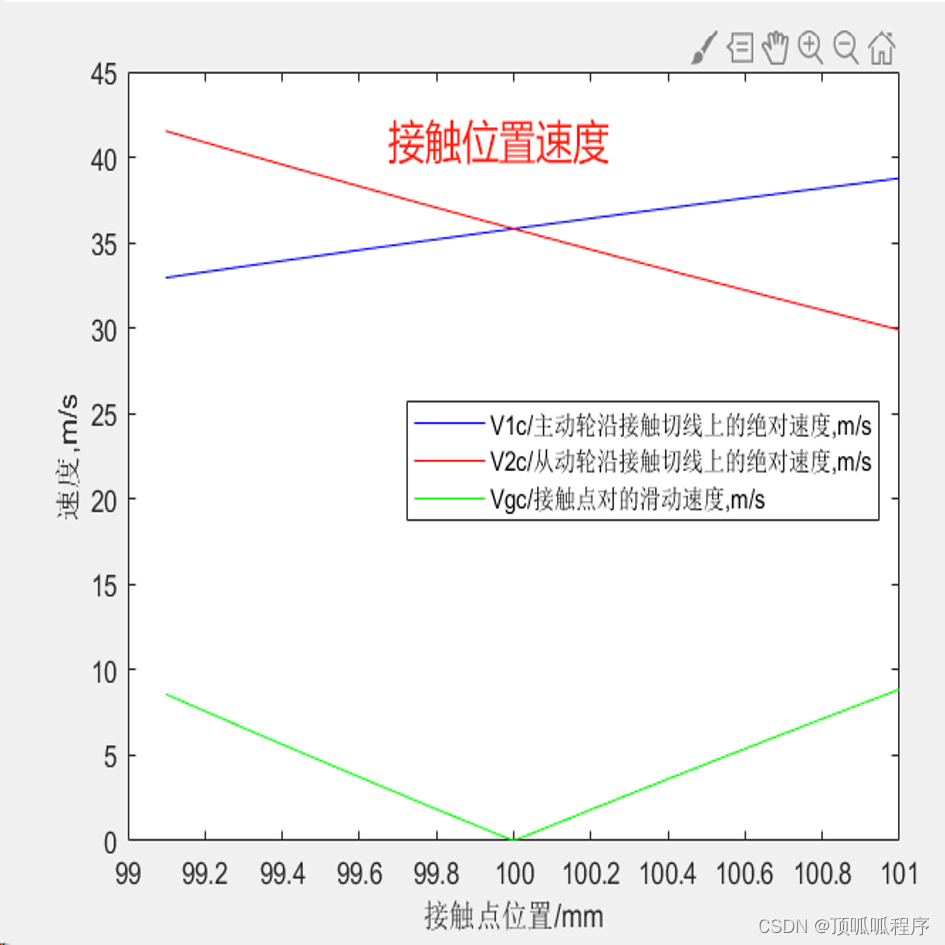
220 基于matlab的考虑直齿轮热弹耦合的动力学分析
基于matlab的考虑直齿轮热弹耦合的动力学分析,输入主动轮、从动轮各类参数,考虑润滑油温度、润滑油粘度系数等参数,输出接触压力、接触点速度、摩擦系数、对流传热系数等结果。程序已调通,可直接运行。 220直齿轮热弹耦合 接触压力…...
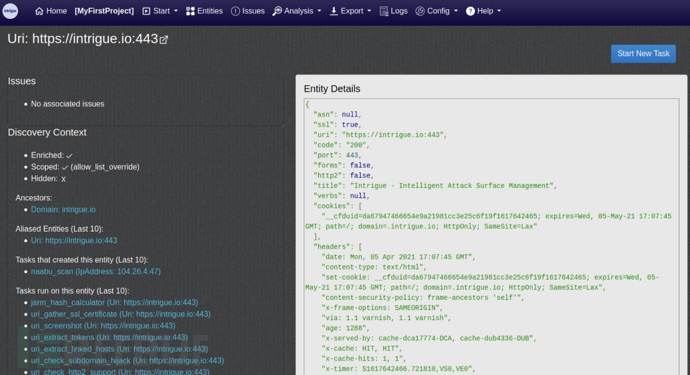
Intrigue Core:一款功能强大的攻击面枚举引擎
关于Intrigue Core Intrigue Core是一款功能强大的开源攻击面枚举引擎,该工具可以帮助广大研究人员更好地管理应用程序的攻击面。 Intrigue Core集成了各种各样的安全数据源,可以将这些数据提取到标准化的对象模型中,并通过图形数据库跟踪关…...

【精品PPT】智慧路灯大数据平台整体建设实施方案(免费下载)
1、知识星球下载: 如需下载完整PPTX可编辑源文件,请前往星球获取:https://t.zsxq.com/19QeHVt8y 2、免费领取步骤: 【1】关注公众号 方案驿站 【2】私信发送 【智慧路灯大数据平台】 【3】获取本方案PDF下载链接,直…...
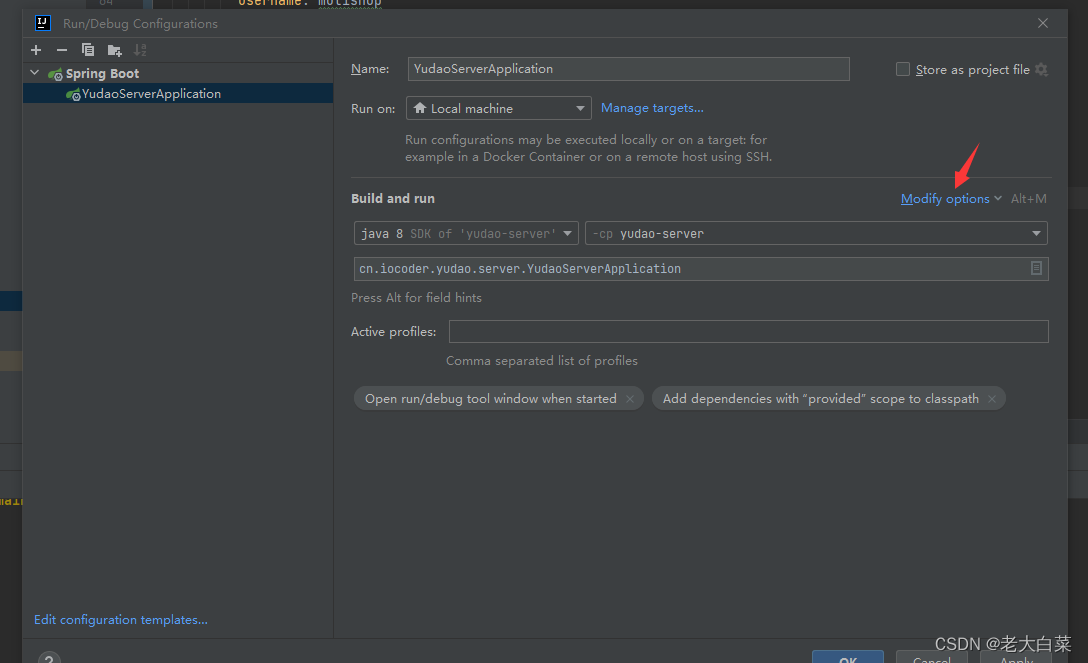
idea 中运行spring boot 项目报 Command line is too long的解决办法。
Command line is too long 在这里选择edit configures 选择shrten command line , 选择 jar manifest 运行即可。...

Windows终端添加git bash
环境:windows11 终端:windows terminal git bash默认的界面不太好看,添加到终端会比较好用 步骤 打开 windows terminal,在向下箭头 点击 设置左侧栏 点击 “添加新配置文件”,如下图配置,主要修改项&…...
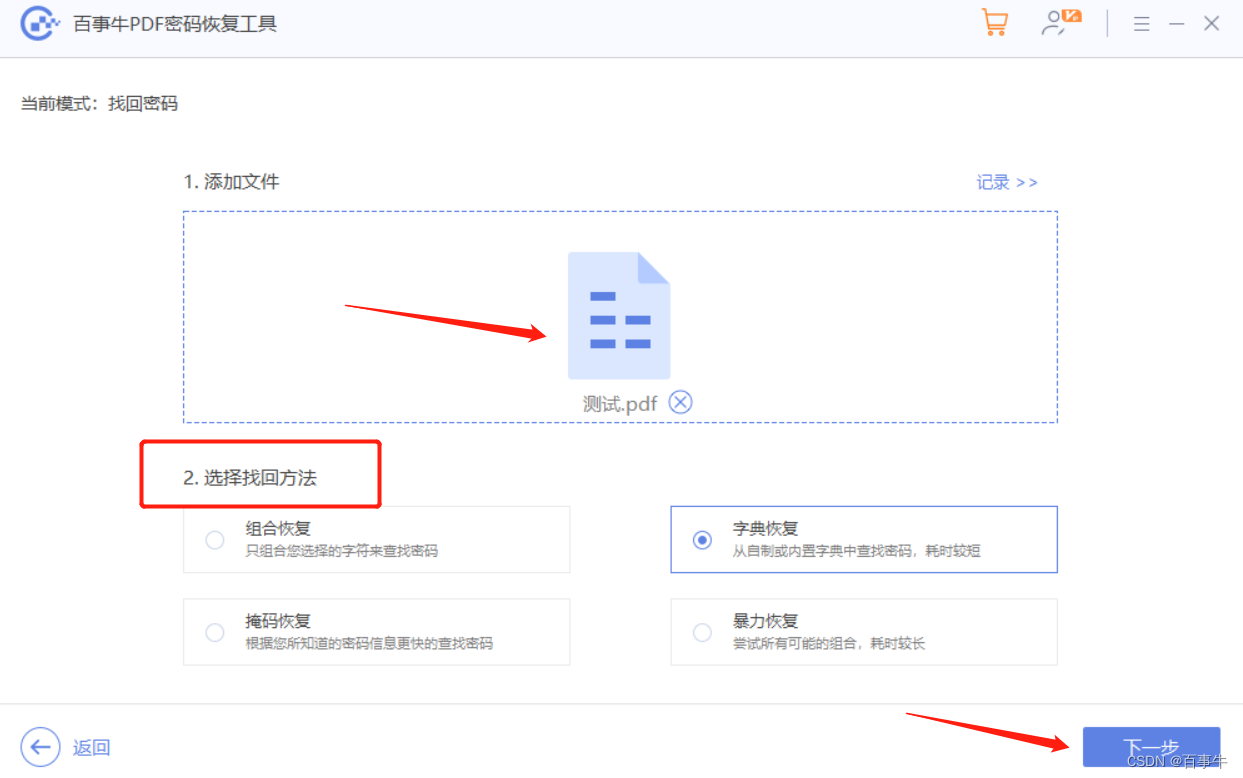
【方法】PDF密码如何取消?
对于重要的PDF文件,很多人会设置密码保护,那后续不需要保护了,如何取消密码呢? 今天我们来看看,PDF的两种密码,即“限制密码”和“打开密码”,是如何取消的,以及忘记密码的情况要怎…...
怎么开发一个预约小程序_一键预约新体验
预约小程序,让生活更便捷——轻松掌握未来,一键预约新体验 在快节奏的现代生活中,我们总是在不断地奔波,为了工作、为了生活,不停地忙碌着。然而,在这繁忙的生活中,我们是否曾想过如何更加高效…...
JavaScript_注释数据类型
JavaScript_语法_注释&数据类型: 1.2注释: 1.单行注释://注释内容 2.多行注释:/*注释内容*/ 1.3数据类型: 1.原始数据类型(基本数据类型):(只有这五种) 1.number:数字…...

蓝桥杯2020年第十一届省赛 CC++ 研究生组2.0
约数个数 #include<iostream> #include<cmath> using namespace std; int main(){int n 78120, ans 0, sqr sqrt(n);for(int i 1; i < sqr; i){if(n % i 0){ans;//printf("%d,", i);if(i * i ! n) {ans;//printf("%d,", n / i);}}}//…...

SOCKS5代理、代理IP、跨界电商、游戏技术与网络安全的综合探讨
在全球经济一体化的大背景下,"出海"已成为许多企业尤其是电商和游戏行业的重要战略方向。然而,随着企业业务的扩展到海外市场,网络安全、数据隐私和内容访问等问题也随之而来。本文将深入探讨SOCKS5代理、代理IP在跨界电商和游戏行…...

关于HTTP1.0、1.1、1.x、2.0、3.0与HTTPS之间的理解
关于HTTP1.0、1.1、1.x、2.0、3.0与HTTPS之间的理解 HTTP的由来 HTTP是Hyper Text Transfer Protocol(超文本传输协议)的缩写。它的发展是万维网协会(World Wide Web Consortium)和Internet工作小组IETF(Internet Eng…...

useRef总结
一、使用ref引用值 在react中ref的主要用途是用来获取DOM元素或者某个组件实例的引用。当你想访问真实的DOM节点,或者需要在组件之间共享可变数据且不需要触发重新渲染时,通常会使用ref。在vue中ref是响应式的,当数据发生改变时,相…...

计算机网络知识等汇总补充
计算机网络知识汇总补充 一、四次挥手1、为什么TCP要等待2MSL2、如果说一个系统中,有大量的time_wait和close_wait,会是什么原因? 二、你是怎么解决粘包问题?三、你觉得哪些场景适合redis四、redis的持久化策略五、你会怎么保证my…...

word中插入mathtype版的符号后,行间距变大解决方法
问题 解决方法 选中该段,设置固定值行距。如果是宋体,小四,1.25行距,那么固定值就为20磅。 成功解决。...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
