订单中台架构:打造高效订单管理系统的关键
在现代商业环境下,订单管理对于企业来说是至关重要的一环。然而,随着业务规模的扩大和多渠道销售的普及,传统的订单管理方式往往面临着诸多挑战,如订单流程复杂、信息孤岛、数据不一致等问题。为了应对这些挑战并抓住订单管理的机遇,订单中台架构应运而生。
1. 什么是订单中台架构?
订单中台架构是指以订单为核心,通过将订单相关的业务逻辑和数据进行整合,构建统一的订单管理平台。它将传统的订单处理流程进行拆解和重组,实现了订单全生命周期的管控和协同。同时,订单中台架构还可以与企业的其他系统进行集成,提供全面的订单管理能力。
2. 为什么需要订单中台架构?
订单中台架构具有以下几个关键优势:
- 统一订单管理:订单中台架构将各个渠道的订单数据集中管理,消除了信息孤岛和数据不一致的问题,实现了订单数据的一致性和可靠性。
- 灵活定制订单流程:通过订单中台架构,企业可以根据自身业务需求灵活定制订单处理流程,提高订单处理效率和响应速度。
- 强大的数据分析能力:订单中台架构可以对订单数据进行全面的分析和挖掘,帮助企业深入了解订单趋势、客户需求等,为经营决策提供有力支持。
- 异常处理和监控:订单中台架构可以实时监控订单状态和交付情况,及时发现异常情况并进行处理,提高订单交付的准确性和可靠性。
3. 实施订单中台架构的关键步骤
实施订单中台架构需要经过以下几个关键步骤:
- 分析与设计:对企业的订单管理流程进行分析和设计,明确各个环节的职责和数据流动。
- 整合与集成:将各个订单相关的系统进行整合和集成,确保订单数据的一致性和完整性。
- 开发与部署:根据设计方案进行订单中台平台的开发和部署,确保系统稳定运行。
- 测试与优化:对订单中台系统进行全面测试,及时发现并修复问题,不断优化系统性能和用户体验。
- 迁移与上线:将已有订单数据迁移至订单中台系统,并进行上线和正式启用。
结论:订单中台架构的未来发展
订单中台架构作为提升企业订单管理效率和质量的关键手段,将在未来得到更广泛的应用和发展。随着技术的不断进步和业务的不断变化,订单中台架构也将不断演进和完善,为企业提供更强大的订单管理能力和更优质的订单服务。通过采用订单中台架构,企业可以在竞争激烈的市场环境下取得更大的竞争优势,实现业务增长和客户满意度的双赢局面。
相关文章:

订单中台架构:打造高效订单管理系统的关键
在现代商业环境下,订单管理对于企业来说是至关重要的一环。然而,随着业务规模的扩大和多渠道销售的普及,传统的订单管理方式往往面临着诸多挑战,如订单流程复杂、信息孤岛、数据不一致等问题。为了应对这些挑战并抓住订单管理的机…...
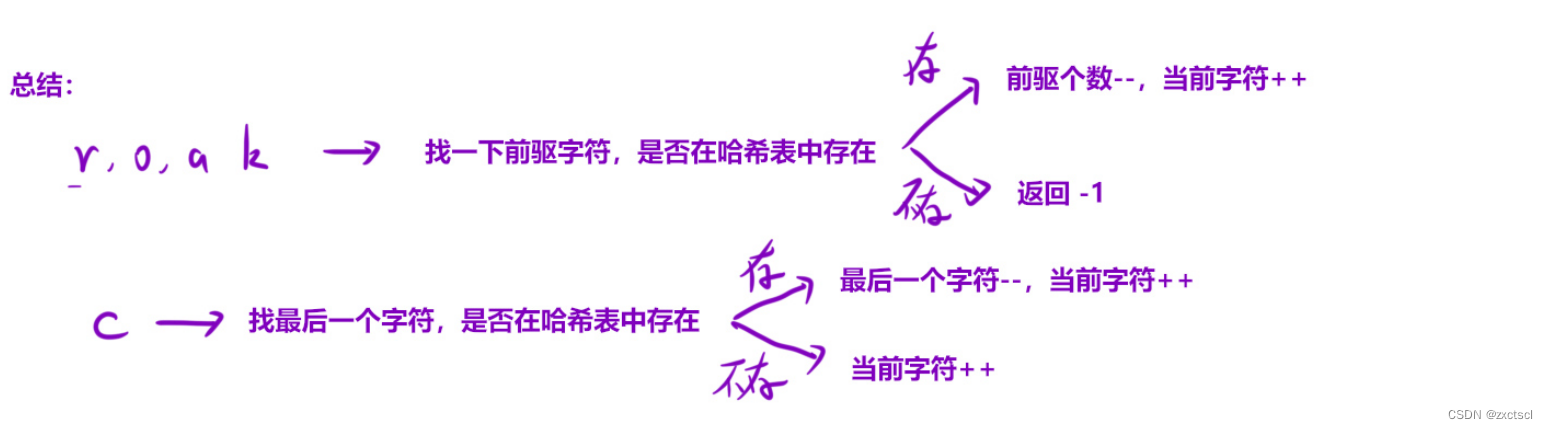
【算法】模拟
个人主页 : zxctscl 如有转载请先通知 题目 前言1. 1576. 替换所有的问号1.1 分析1.2 代码 2. 495. 提莫攻击2.1 分析2.2 代码 3. 6. Z 字形变换3.1 分析3.2 代码 4. 38. 外观数列4.1 分析4.2 代码 5. 1419. 数青蛙5.1 分析5.2 代码 前言 模拟算法就是根据题目所给…...

电力综合自动化系统对电力储能技术的影响有哪些?
电力综合自动化系统对电力储能技术的影响主要体现在以下几个方面: 提高能源利用效率:电力综合自动化系统通过优化调度和能量管理,可以实现储能设备的有效利用,提高能源利用效率。在电力系统中,储能设备可以有效地平抑风…...

Compose UI 之 Card 卡片组件
Card Card 是用于显示带有圆角和可选阴影的矩形内容容器。它通常用于构建用户界面,并可以包含标题、文本、图像、按钮等元素,表示界面上的可交互元素,我们称它是 “卡片”。 Card 使用的一些经典的场景: 列表数据,例如 新闻列表,产品列表等。信息提示框,使用 Card 组件…...
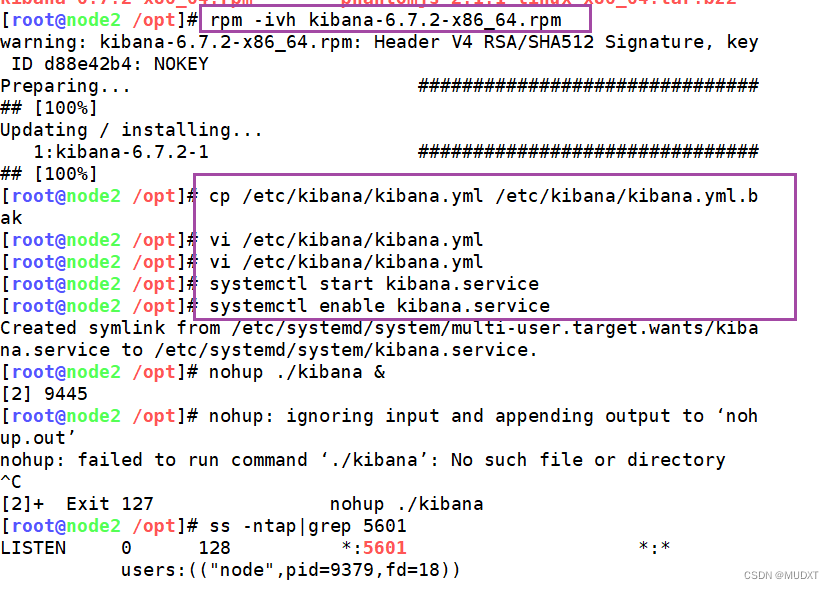
ELK日志
...

WPF Pack
在WPF中,Pack URI(Uniform Resource Identifier)是一种特殊格式的统一资源标识符,用于定位和访问应用程序内部或外部的各种资源,如XAML文件、图像、样式、字体等。这种机制允许开发者以标准化、平台无关的方式引用和打…...

计算两个时间段的差值
计算两个时间段的差值 运行效果: 代码实现: #include<stdio.h>typedef struct {int h; // 时int m; // 分int s; // 秒 }Time;void fun(Time T[2], Time& diff) {int sum_s[2] { 0 }; for (int i 0; i < 1; i) { // 统一为秒数sum_s[…...
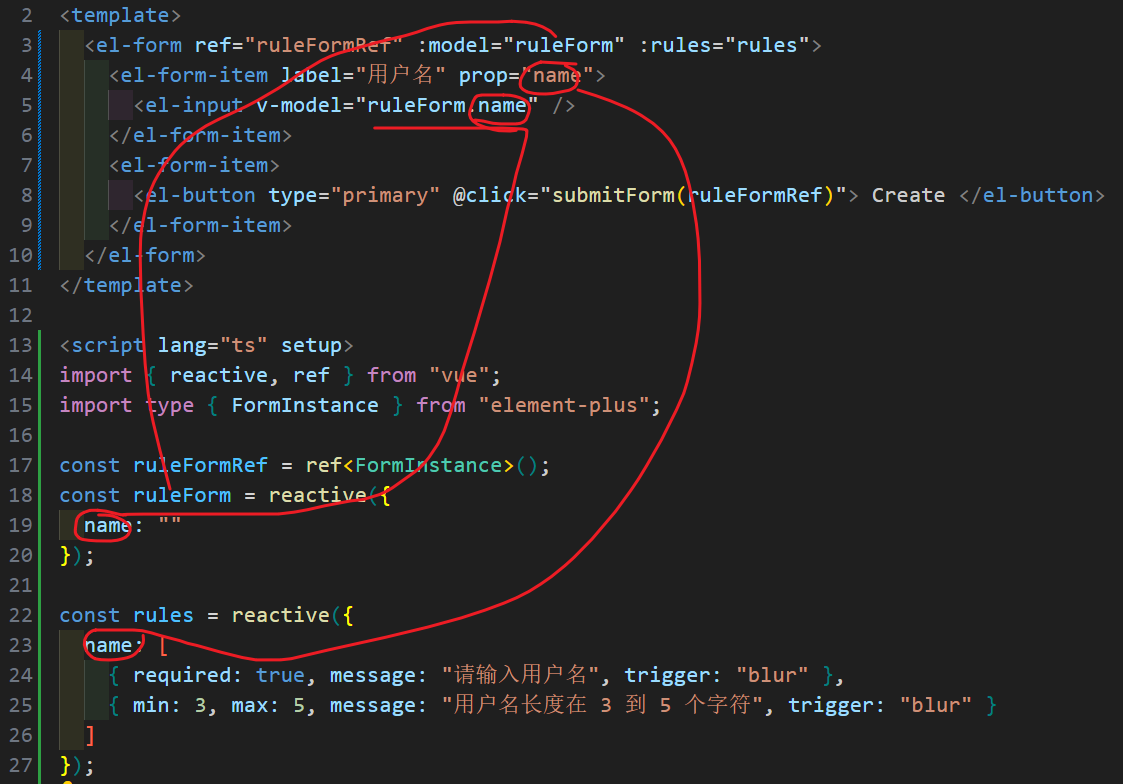
Element Plus 表单校验
原理 为 rules 属性传入约定的验证规则,并将 form-Item 的 prop 属性设置为需要验证的特殊键值:model和:rules中字段的名称需要一致 示例: <template><el-form ref"ruleFormRef" :model"ruleForm" :rules"rules&q…...
java实现TCP交互
服务器端 import java.io.IOException; import java.io.InputStream; import java.io.OutputStream; import java.io.PrintWriter; import java.net.ServerSocket; import java.net.Socket; import java.util.PriorityQueue; import java.util.Scanner;public class TCP_Serv…...

学习云计算HCIE选择誉天有什么优势?
誉天云计算课程优势实战性强 课程注重实践操作,通过实际案例和实验操作,让学员深入了解云计算的应用场景和实际操作技能。课程内容全面 涵盖所有云计算涉及的IT基础知识、服务器、存储、网络等方面的基础知识,开源操作系统Linux,开…...
python之文件操作与管理
1、文件操作 通过open()操作,来创建文件对象,下面是open()函数语法如下: open(file,mode r,buffering -1 , encoding None ,errors None , newline None,closefd True,opener …...

大厂Java笔试题之对完全数的处理
题目:完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。 它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。 例如&…...

【Redis深度解析】揭秘Cluster(集群):原理、机制与实战优化
Redis Cluster是Redis官方提供的分布式解决方案,通过数据分片与节点间通信机制,实现了水平扩展、高可用与数据容灾。本文将深入剖析Redis Cluster的工作原理、核心机制,并结合实战经验分享优化策略,为您打造坚实可靠的Redis分布式…...

【JAVA基础篇教学】第六篇:Java异常处理
博主打算从0-1讲解下java基础教学,今天教学第五篇: Java异常处理。 异常处理是Java编程中重要的一部分,它允许开发人员在程序运行时检测和处理各种错误情况,以保证程序的稳定性和可靠性。在Java中,异常被表示为对象&am…...
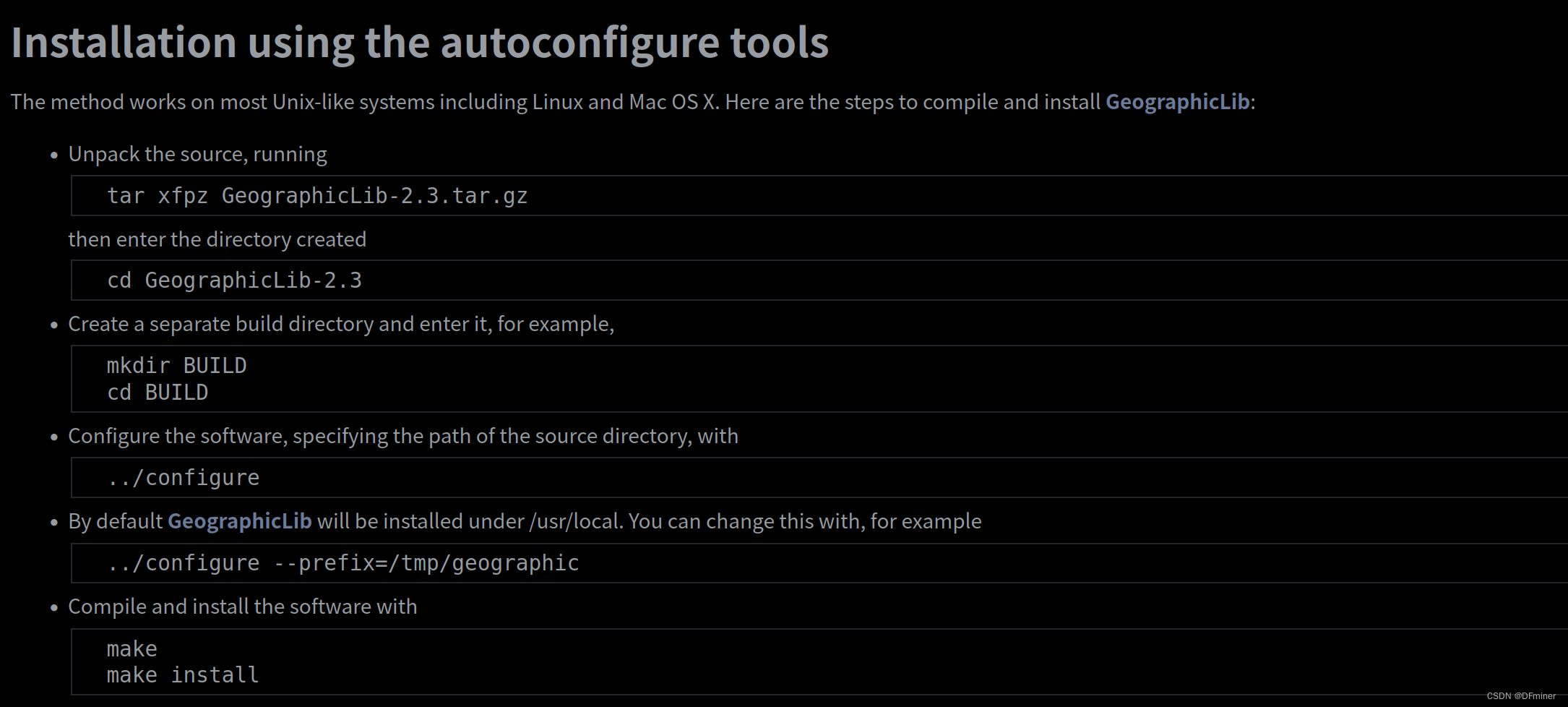
【ubuntu20.04】安装GeographicLib
下载地址 GeographicLib: Installing GeographicLib 我们是ubuntu20.04 ,所以下载第一个 GeographicLib-2.3.tar.gz 接着跟着官方步骤安装,会出错!!!!马的 官方错误示例:tar xfpz Geographi…...
 Vue-Router的使用与配置)
从0开始搭建基于VUE的前端项目(四) Vue-Router的使用与配置
版本 vue-router 3.6.5 (https://v3.router.vuejs.org/zh/) 安装 安装要指定版本,默认安装的4版本的 npm install vue-router3.6.5代码实现 在src目录下创建router目录 router/index.js import Vue from vue import Router from vue-routerVue.use(Router)con…...

力扣爆刷第117天之CodeTop100五连刷71-75
力扣爆刷第117天之CodeTop100五连刷71-75 文章目录 力扣爆刷第117天之CodeTop100五连刷71-75一、48. 旋转图像二、39. 组合总和三、113. 路径总和 II四、34. 在排序数组中查找元素的第一个和最后一个位置五、394. 字符串解码 一、48. 旋转图像 题目链接:https://le…...
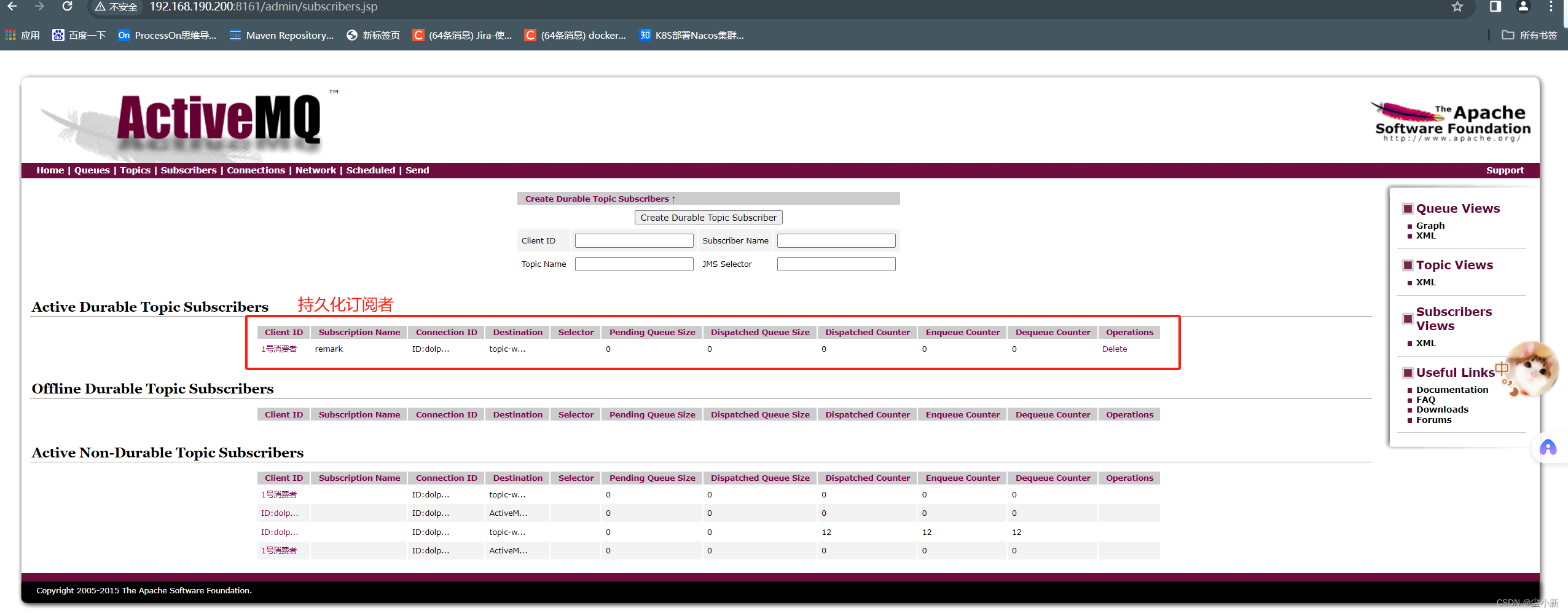
ActiveMQ入门案例(queue模式和topic模式)
目录 前言:为什么使用消息中间件? 异步通信 缓冲 解耦 前提:安装并启动activemq 一、点对点(point to point, queue) 1.1 创建maven项目 1.2 Pom依赖 1.2 JmsProduce 消息生产者 1.3 JmsConsumer…...

2024年最新云服务器ECS租用报价费用表-阿里云
阿里云服务器租用价格表2024年最新,云服务器ECS经济型e实例2核2G、3M固定带宽99元一年,轻量应用服务器2核2G3M带宽轻量服务器一年61元,ECS u1服务器2核4G5M固定带宽199元一年,2核4G4M带宽轻量服务器一年165元12个月,2核…...

第四百五十四回
文章目录 1. 问题描述2. 优化方法2.1 缩小范围2.2 替代方法 3. 示例代码4. 内容总结 我们在上一章回中介绍了"如何获取AppBar的高度"相关的内容,本章回中将介绍关于MediaQuery的优化.闲话休提,让我们一起Talk Flutter吧。 1. 问题描述 我们在…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
