算法打卡day33
今日任务:
1)509. 斐波那契数
2)70. 爬楼梯
3)746.使用最小花费爬楼梯
509. 斐波那契数
题目链接:509. 斐波那契数 - 力扣(LeetCode)
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。示例 1: 输入:2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2: 输入:3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3: 输入:4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示: 0 <= n <= 30
文章讲解:代码随想录 (programmercarl.com)
视频讲解:手把手带你入门动态规划 | LeetCode:509.斐波那契数哔哩哔哩bilibili
思路:
- 首先定义一个列表
f来存储斐波那契数列的值,初始包含前两项 [0, 1]。- 如果 n 小于等于 1,则直接返回列表中对应位置的值。
- 否则,使用循环从 2 开始遍历到 n,依次计算每一项的值,并添加到列表
f中。- 最后返回列表中索引为 n 的值,即为斐波那契数列的第 n 项
class Solution:def fib(self, n: int) -> int:# 初始化斐波那契数列的前两项f = [0, 1]# 如果 n 小于等于 1,则直接返回对应位置的值if n <= 1:return f[n]# 使用循环计算斐波那契数列的第 n 项for x in range(2, n + 1):# 计算第 x 项的值,并添加到列表中f.append(f[x - 1] + f[x - 2])# 返回斐波那契数列的第 n 项return f[n]这种比较好理解,立马能想到,这里面可以优化的部分在空间复杂度,上面代码空间复杂度O(n)
我们可以定义一个长度为3的列表,反复更新这三个数即可。空间复杂度O(3)
也可以定义3个变量,反复更新3个变量。空间复杂度O(1)
class Solution:# 空间复杂度O(3)def fib(self, n: int) -> int:if n <= 1:return ndp = [0, 1]for i in range(2, n + 1):total = dp[0] + dp[1]dp[0] = dp[1]dp[1] = totalreturn dp[1]# 空间复杂度O(1)def fib(self, n: int) -> int:if n <= 1:return nprev1, prev2 = 0, 1for _ in range(2, n + 1):curr = prev1 + prev2prev1, prev2 = prev2, currreturn prev270. 爬楼梯
题目链接:70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数。示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1 阶 + 1 阶 2 阶示例 2: 输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1 阶 + 1 阶 + 1 阶 1 阶 + 2 阶 2 阶 + 1 阶
文章讲解:代码随想录 (programmercarl.com)
视频讲解:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目哔哩哔哩bilibili
思路:
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
- 首先定义一个列表
f来存储爬楼梯的方法数,初始包含前三项 [0, 1, 2]。其中 f[0] 为占位符,不参与计算。- 如果 n 小于 3,则直接返回列表中对应位置的值。
- 否则,使用循环从 3 开始遍历到 n,依次计算每一项的值,并添加到列表
f中。每一项的值都等于前两项和前一项的和,因为可以选择爬一阶或者爬两阶台阶。- 最后返回列表中索引为 n 的值,即为爬楼梯的方法数。
class Solution:def climbStairs(self, n: int) -> int:f = [0,1,2]if n < 3:return f[n]for x in range(3,n+1):f.append(f[x-1]+f[x-2])return f[n]# 空间复杂度为O(3)版本def climbStairs(self, n: int) -> int:if n <= 1:return nf = [0] * 3f[1] = 1f[2] = 2for i in range(3, n + 1):total = f[1] + f[2]f[1] = f[2]f[2] = totalreturn f[2]# 空间复杂度为O(1)版本def climbStairs2(self, n: int) -> int:if n <= 1:return nprev1 = 1prev2 = 2for i in range(3, n + 1):total = prev1 + prev2prev1 = prev2prev2 = totalreturn prev2746.使用最小花费爬楼梯
题目链接:746. 使用最小花费爬楼梯 - 力扣(LeetCode)
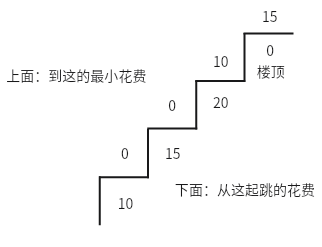
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。示例 1: 输入:cost = [10, 15, 20] 输出:15 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。示例 2: 输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 输出:6 解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。提示: cost 的长度范围是 [2, 1000]。 cost[i] 将会是一个整型数据,范围为 [0, 999]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯哔哩哔哩bilibili
思路:
用数组展示如下:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:# 如果台阶数小于2,则不需要花费if len(cost) < 2:return 0# 初始化到达前两个台阶的最低花费cost1 = 0cost2 = 0# 将顶部的台阶花费添加到列表中cost.append(0)# print(f'初始化cost1={cost1},cost2={cost2}')# 从第三个台阶开始计算最低花费for i in range(2, len(cost)):# 计算到达当前台阶的最低花费cost_total = min(cost1 + cost[i - 2], cost2 + cost[i - 1])# 更新前两个台阶的最低花费cost1 = cost2cost2 = cost_total# print(f'i={i},cost1={cost1},cost2={cost2},cost_total={cost_total}')# 返回到达顶部的最低花费return cost2相关文章:

算法打卡day33
今日任务: 1)509. 斐波那契数 2)70. 爬楼梯 3)746.使用最小花费爬楼梯 509. 斐波那契数 题目链接:509. 斐波那契数 - 力扣(LeetCode) 斐波那契数,通常用 F(n) 表示,形成…...
《疯狂java讲义》Java AWT图形化编程中文显示
《疯狂java讲义》第六版第十一章AWT中文没有办法显示问题解决 VM Options设置为-Dfile.encodinggbk 需要增加变量 或者这边直接设置gbk 此外如果用swing 就不会产生这个问题了。...

Python3 标准库,API文档链接
一、标准库 即当你安装python3 后就自己携带的一些已经提供好的工具模块,工具类,可以专门用来某一类相关问题,达到辅助日常工作或者个人想法的一些成品库 类似的 C ,Java 等等也都有自己的标准库和使用文档 常见的一些: os 模块…...
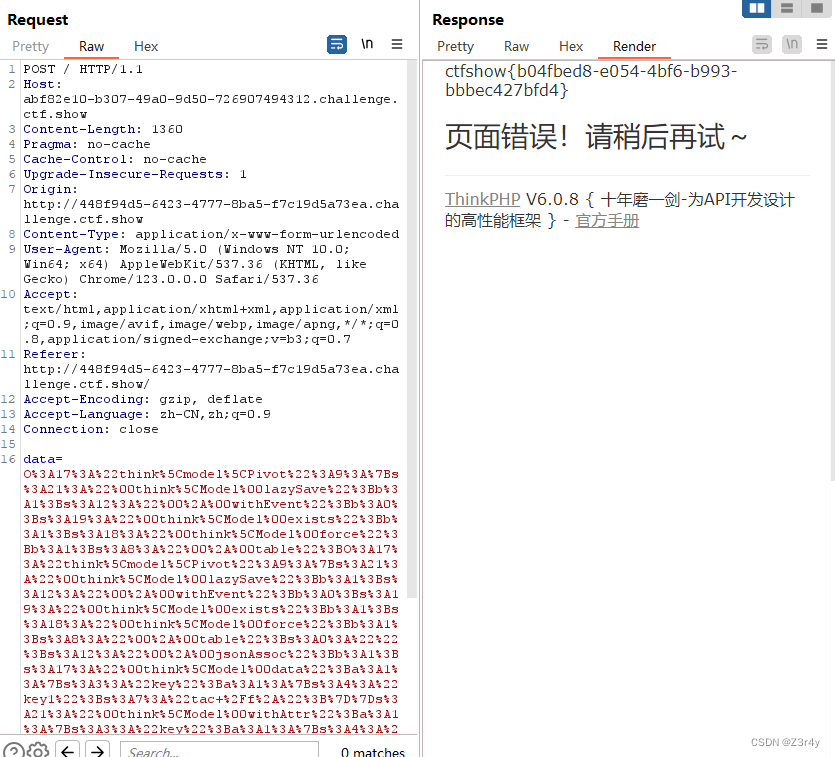
【Web】CTFSHOW-ThinkPHP5-6反序列化刷题记录(全)
目录 web611 web612 web613-622 web623 web624-626 纯记录exp,链子不作赘述 web611 具体分析: ThinkPHP-Vuln/ThinkPHP5/ThinkPHP5.1.X反序列化利用链.md at master Mochazz/ThinkPHP-Vuln GitHub 题目直接给了反序列化入口 exp: <?ph…...

AR智能眼镜方案_MTK平台安卓主板芯片|光学解决方案
AR眼镜作为一种引人注目的创新产品,其芯片、显示屏和光学方案是决定整机成本和性能的关键因素。在这篇文章中,我们将探讨AR眼镜的关键技术,并介绍一种高性能的AR眼镜方案,旨在为用户带来卓越的体验。 AR眼镜的芯片选型至关重要。一…...
Android网络抓包--Charles
一、Android抓包方式 对Https降级进行抓包,降级成Http使用抓包工具对Https进行抓包 二、常用的抓包工具 wireshark:侧重于TCP、UDP传输层,HTTP/HTTPS也能抓包,但不能解密HTTPS报文。比较复杂fiddler:支持HTTP/HTTPS…...
)
【LeetCode热题100】238. 除自身以外数组的乘积(数组)
一.题目要求 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 **不要使用除法,**且在…...
《哈迪斯》自带的Lua解释器是哪个版本?
玩过《哈迪斯》(英文名:Hades)吗?最近在研究怎么给这款游戏做MOD,想把它的振动体验升级到更高品质的RichTap。N站下载了一些别人做的MOD,发现很多都基于相同的格式,均是对游戏.sjon文件或.lua文…...

Java内存泄漏内存溢出
1.定义 OOM内存溢出是指应用程序尝试使用更多内存资源,而系统无足够的内存,导致程序崩溃。 内存泄漏是指应用程序中分配的内存未能被正确释放,导致系统中的可用内存逐渐减少。 2.内存泄漏的原因 可能包括对象引用未被释放、缓存未被清理等。 …...

【springboot】项目启动时打印全部接口方法
方法:在你springboot项目的基础上,创建下面的类: package com.llq.wahaha.listener;import org.springframework.beans.factory.annotation.Autowired; import org.springframework.context.ApplicationContext; import org.springframework…...

单例19c RMAN数据迁移方案
一、环境说明 源库 目标库 IP 192.168.37.200 192.168.37.202 系统版本 RedHat 7.9 RedHat 7.9 数据库版本 19.3.0.0.0 19.3.0.0.0 SID beg beg hostname beg rman 数据量 1353M 说明:源库已经创建数据库实例,并且存在用户kk和他创建的表空间…...
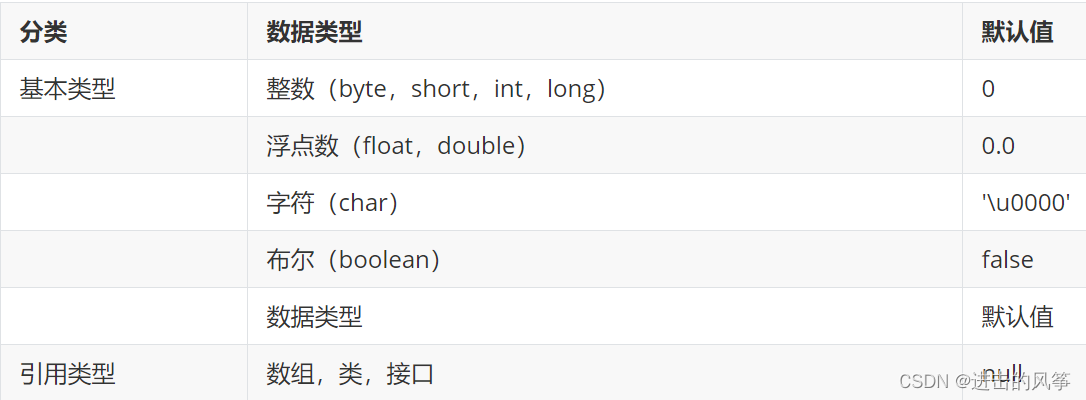
05—面向对象(上)
一、面向对象编程 1、类和对象 (1)什么是类 类是一类具有相同特性的事物的抽象描述,是一组相关属性和行为的集合。 属性:就是该事物的状态信息。行为:就是在你这个程序中,该状态信息要做什么操作&#x…...

【LeetCode热题100】【链表】两数相加
题目链接:2. 两数相加 - 力扣(LeetCode) 基本思路同:【leetcode】大数相加-CSDN博客 数值的位置已经倒过来了,用一个进位记录进位,用一个数记录和,链表到空了就当成0 class Solution { publi…...

Linux命令学习—linux 的硬件管理
1.1、linux 的硬件管理 1.1.1、计算机的硬件管理 在 linux 下,计算机所有设备是以文件的形势存在的。 在 linux 下查看硬件信息 ①、lspci 列出所有的 PCI 设备 ②、fdisk -l 查看存储设备信息 ③、查看/proc 目录下相应的文件来查看一些设备信息 cat /proc/cp…...

通讯录项目(用c语言实现)
一.什么是通讯录 通讯录是一种用于存储联系人信息的工具或应用程序。它是一种电子化的地址簿,用于记录和管理个人、机构或组织的联系方式,如姓名、电话号码、电子邮件地址和邮寄地址等。通讯录的目的是方便用户在需要时查找和联系他人。 通讯录通常以列…...

让大模型落地有“技”可循
“2018年,随着Transformer预训练模型的兴起,自然语言处理(NLP)学术圈中形成了一个主流观点——NLP领域的不同技术方向,如文本分类、文本匹配、序列标注等,最终都会被归结到文本生成这一核心任务之下。”这是…...
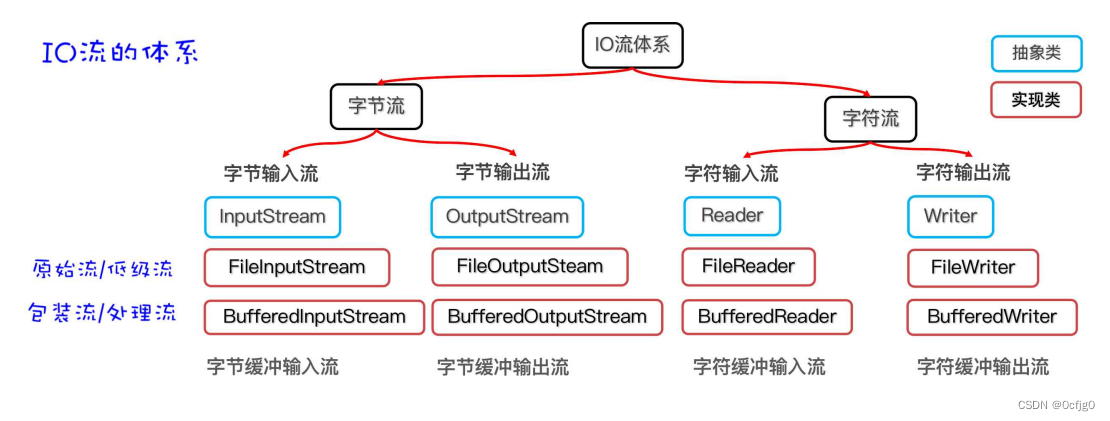
java:字符集和字符流
字符集 规定了字符和二进制之间对应关系的一张表 字节是计算机最基本的存储单位 字符则是通过字符组成和编码而成的文本 常见字符集 1,ASCII字符集 基础字符编码标准,包含128个字符,只包括英文字母,数字和一些常见的符号 一个字节表示一个字符 所有的字符集均兼容ASCII…...

Java常见的设计模式
Java常见的设计模式 工厂模式(Factory Pattern)单例模式(Singleton Pattern)代理模式模式(Proxy Pattern)适配器模式(Adapter Pattern)观察者模式(Observer Pattern&…...
Oracle 19c RAC集群相关日志
1.DB日志(数据库日志) Redo Log(重做日志): 在Oracle数据库中,重做日志记录了数据库发生的所有修改操作,包括数据的插入,更新和删除。在RAC的环境中,每个实例都有自己的重…...
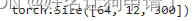
TR4 - Transformer中的多头注意力机制
目录 前言自注意力机制Self-Attention层的具体机制Self-Attention 矩阵计算 多头注意力机制例子解析 代码实现总结与心得体会 前言 多头注意力机制可以说是Transformer中最主要的模块,没有之一。这次我们来仔细分析一下注意力机制与多头注意力机制。 自注意力机制…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...