LeetCode-1143. 最长公共子序列【字符串 动态规划】
LeetCode-1143. 最长公共子序列【字符串 动态规划】
- 题目描述:
- 解题思路一:动规五部曲
- 解题思路二:1维DP
- 解题思路三:0
题目描述:
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ,它的长度为 3 。
示例 2:
输入:text1 = “abc”, text2 = “abc”
输出:3
解释:最长公共子序列是 “abc” ,它的长度为 3 。
示例 3:
输入:text1 = “abc”, text2 = “def”
输出:0
解释:两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。
解题思路一:动规五部曲
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
有同学会问:为什么要定义长度为[0, i - 1]的字符串text1,定义为长度为[0, i]的字符串text1不香么?
这样定义是为了后面代码实现方便,如果非要定义为长度为[0, i]的字符串text1也可以,我在 动态规划:718. 最长重复子数组 (opens new window)中的「拓展」里 详细讲解了区别所在,其实就是简化了dp数组第一行和第一列的初始化逻辑。
- 确定递推公式
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
- dp数组如何初始化
先看看dp[i][0]应该是多少呢?
test1[0, i-1]和空串的最长公共子序列自然是0,所以dp[i][0] = 0;
同理dp[0][j]也是0。
其他下标都是随着递推公式逐步覆盖,初始为多少都可以,那么就统一初始为0。
-
确定遍历顺序
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
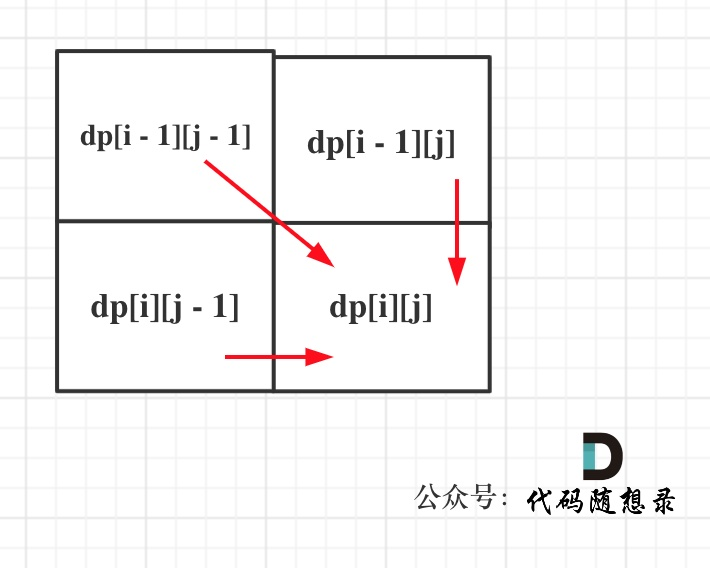 那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵。
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵。 -
举例推导dp数组
以输入:text1 = “abcde”, text2 = “ace” 为例,dp状态如图:
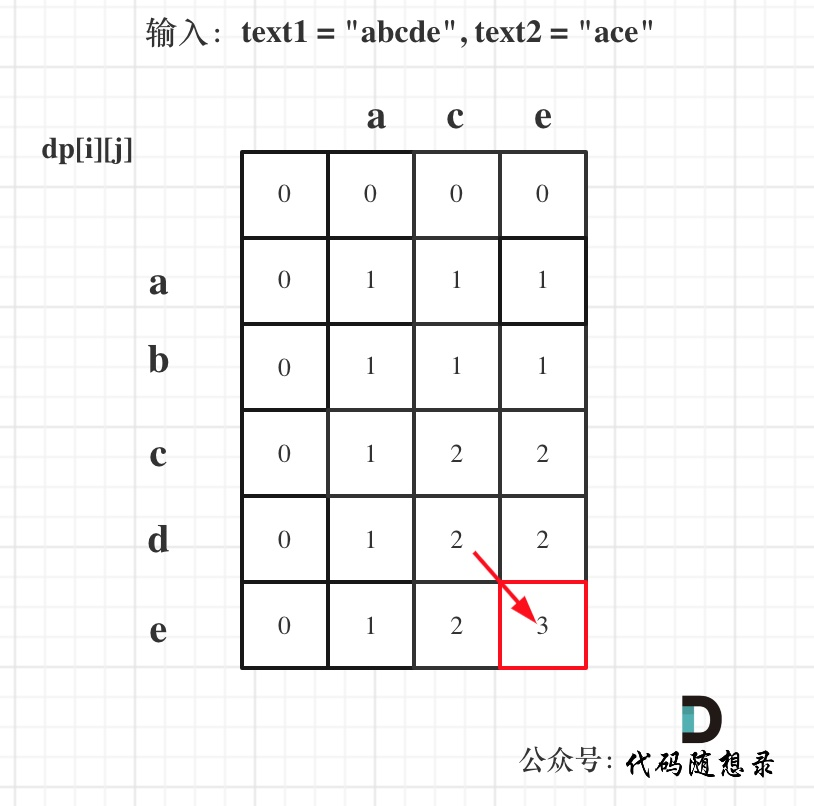
最后红框dp[text1.size()][text2.size()]为最终结果
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:# 创建一个二维数组 dp,用于存储最长公共子序列的长度dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]# 遍历 text1 和 text2,填充 dp 数组for i in range(1, len(text1) + 1):for j in range(1, len(text2) + 1):if text1[i - 1] == text2[j - 1]:# 如果 text1[i-1] 和 text2[j-1] 相等,则当前位置的最长公共子序列长度为左上角位置的值加一dp[i][j] = dp[i - 1][j - 1] + 1else:# 如果 text1[i-1] 和 text2[j-1] 不相等,则当前位置的最长公共子序列长度为上方或左方的较大值dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])# 返回最长公共子序列的长度return dp[len(text1)][len(text2)]# 同意
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:m, n = len(text1), len(text2)dp = [[0] * (n+1) for _ in range(m+1)]for i in range(1, m+1):for j in range(1, n+1):if text1[i-1] != text2[j-1]:dp[i][j] = max(dp[i-1][j], dp[i][j-1])else:dp[i][j] = dp[i-1][j-1] + 1return dp[-1][-1]
时间复杂度:O(nm)
空间复杂度:O(nm)
解题思路二:1维DP
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:m, n = len(text1), len(text2)dp = [0] * (n + 1) # 初始化一维DP数组for i in range(1, m + 1):prev = 0 # 保存上一个位置的最长公共子序列长度for j in range(1, n + 1):curr = dp[j] # 保存当前位置的最长公共子序列长度if text1[i - 1] == text2[j - 1]:# 如果当前字符相等,则最长公共子序列长度加一dp[j] = prev + 1else:# 如果当前字符不相等,则选择保留前一个位置的最长公共子序列长度中的较大值dp[j] = max(dp[j], dp[j - 1])prev = curr # 更新上一个位置的最长公共子序列长度return dp[n] # 返回最后一个位置的最长公共子序列长度作为结果
时间复杂度:O(nm)
空间复杂度:O(n)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)
相关文章:

LeetCode-1143. 最长公共子序列【字符串 动态规划】
LeetCode-1143. 最长公共子序列【字符串 动态规划】 题目描述:解题思路一:动规五部曲解题思路二:1维DP解题思路三:0 题目描述: 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。…...
从0开始创建单链表
前言 这次我来为大家讲解链表,首先我们来理解一下什么是单链表,我们可以将单链表想象成火车 每一节车厢装着货物和连接下一个车厢的链子,单链表也是如此,它是将一个又一个的数据封装到节点上,节点里不仅包含着数据&…...

STC89C52学习笔记(十)
STC89C52学习笔记(十) 综述:本文介绍了DS18B20和单总线协议,以及讲述了如何使用DS18B20测量温度。 一、单总线协议 1.只有一根通讯线:DQ (常见的运用单总线的两种设备:DS18B20和DHT11&#…...
初识二叉树和二叉树的基本操作
目录 一、树 1.什么是树 2. 与树相关的概念 二、二叉树 1.什么是二叉树 2.二叉树特点 3.满二叉树与完全二叉树 4.二叉树性质 相关题目: 5.二叉树的存储 6.二叉树的遍历和基本操作 二叉树的遍历 二叉树的基本操作 一、树 1.什么是树 子树是不相交的;…...

如何开辟动态二维数组(C语言)
1. 开辟动态二维数组 C语言标准库中并没有可以直接开辟动态二维数组的函数,但我们可以通过动态一维数组来模拟动态二维数组。 二维数组其实可以看作是一个存着"DataType []"类型数据的一维数组,也就是存放着一维数组地址的一维数组。 所以&…...
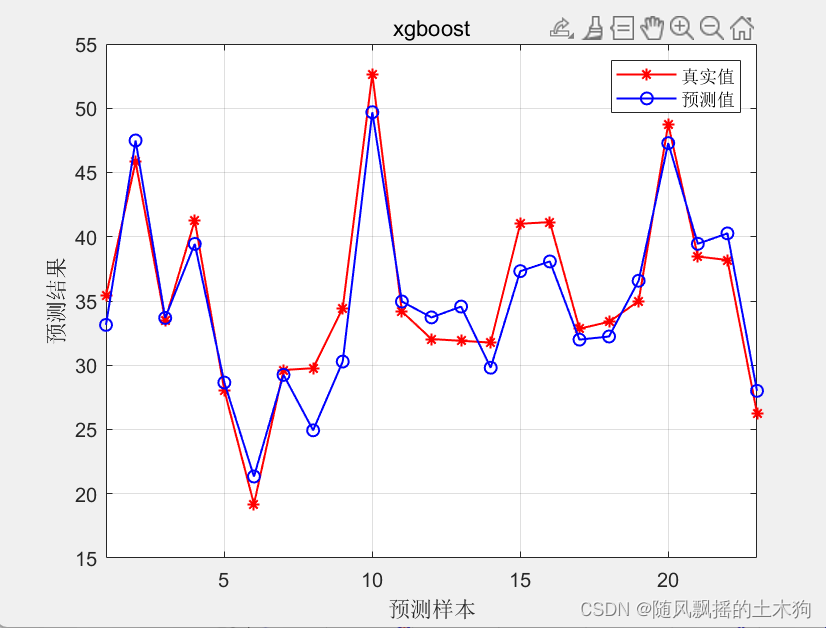
【MATLAB第104期】基于MATLAB的xgboost的敏感性分析/特征值排序计算(针对多输入单输出回归预测模型)
【MATLAB第104期】基于MATLAB的xgboost的敏感性分析/特征值排序计算(针对多输入单输出回归预测模型) 因matlab的xgboost训练模型不含敏感性分析算法,本文通过使用single算法,即单特征因素对输出影响进行分析,得出不同…...

C语言程序与设计——工程项目开发
之前我们已经了解了C语言的基础知识部分,掌握这些之后,基本就可以开发一些小程序了。在开发时,就会出现合作的情况,C语言是如何协作开发的呢,将在这一篇文章进行演示。 工程项目开发 在开发过程中,你接到…...

【Java核心技术】第6章 接口
1 接口 接口不是类,而是对希望符合这个接口的类的一组需求 1.1 Comparable 接口 要对对象进行比较,就要实现(implement)比较(comparable)接口 注意: implements Comparable<Manager> Comparable接口是泛型接口 class Manager exten…...

【Java探索之旅】从输入输出到猜数字游戏
🎥 屿小夏 : 个人主页 🔥个人专栏 : Java编程秘籍 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言一、输入输出1.1 输出到控制台1.2 从键盘输入 二、猜数字游戏2.1 所需知识:…...

【动态规划】【01背包】Leetcode 1049. 最后一块石头的重量 II
【动态规划】【01背包】Leetcode 1049. 最后一块石头的重量 II 解法 ---------------🎈🎈题目链接🎈🎈------------------- 解法 😒: 我的代码实现> 动规五部曲 ✒️确定dp数组以及下标的含义 dp[j]表示容量为…...

2023 年上海市大学生程序设计竞赛 - 四月赛
A. 宝石划分 A. 宝石划分 - 2023 年上海市大学生程序设计竞赛 - 四月赛 - ECNU Online Judge 找距离N最近的M的因数q,输出M/q 如果是暴力所的话,会超时 #include <bits/stdc.h> using namespace std; int main(){ios::sync_with_stdio(false)…...

别让这6个UI设计雷区毁了你的APP!
一款成功的APP不仅仅取决于其功能性,更取决于用户体验,这其中,UI设计又至关重要。优秀的UI设计能够为用户带来直观、愉悦的交互体验,甚至让用户“一见钟情”,从而大大提高产品吸引力。 然而,有很多设计师在…...

继承【C/C++复习版】
目录 一、什么是继承?怎么定义继承? 二、继承关系和访问限定符? 三、基类和派生类对象可以赋值转换吗? 四、什么是隐藏?隐藏vs重载? 五、派生类的默认成员函数? 1)派生类构造函…...

题目 2694: 蓝桥杯2022年第十三届决赛真题-最大数字【暴力解法】
最大数字 原题链接 🥰提交结果 思路 对于每一位,我我们都要尽力到达 9 所以我们去遍历每一位, 如果是 9 直接跳过这一位 如果可以上调到 9 我们将这一位上调到 9 ,并且在a 中减去对应的次数 同样的,如果可以下调到 9,我…...

【C语言】- C语言字符串函数详解
C语言字符串函数详解 1、void *memset(void *dest, int c, size_t count); 将dest前面count个字符置为字符c. 返回dest的值. 2、void *memmove(void *dest, const void *src, size_t count); 从src复制count字节的字符到dest. 如果src和dest出现重叠, 函数会自动处理. 返回…...
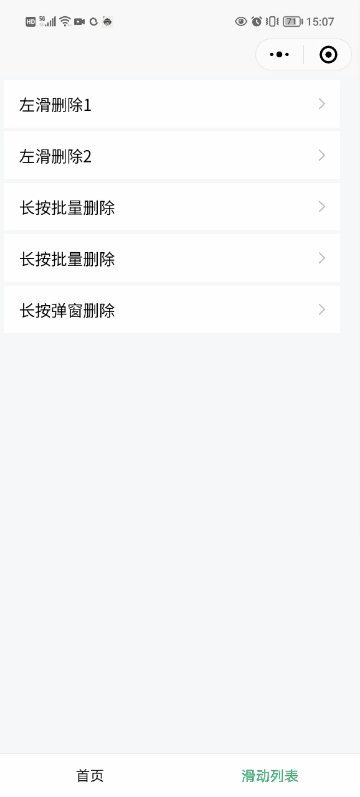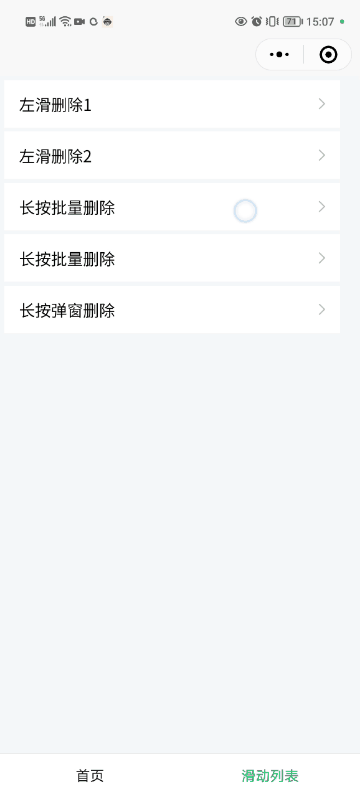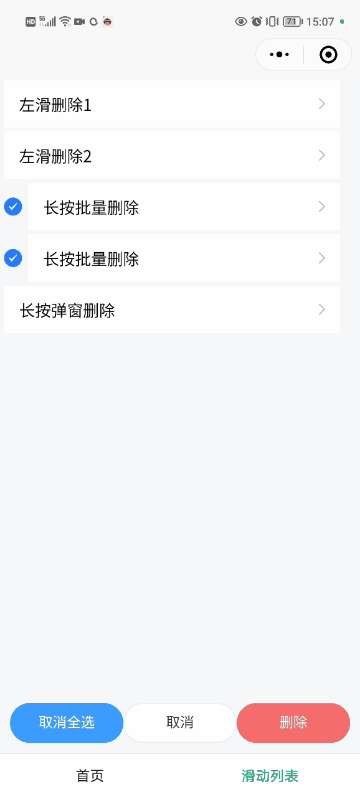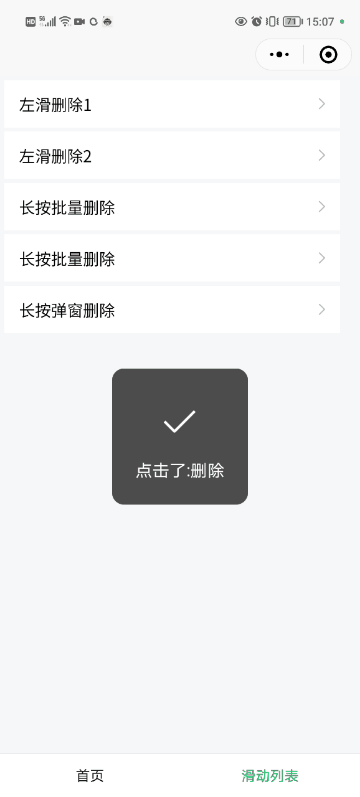
如何实现小程序滑动删除组件+全选批量删除组件
如何实现小程序滑动删除组件全选批量删除组件 一、简介 如何实现小程序滑动删除组件全选批量删除组件 采用 uni-app 实现,可以适用微信小程序、其他各种小程序以及 APP、Web等多个平台 具体实现步骤如下: 下载开发者工具 HbuilderX进入 【Dcloud 插…...

基于SSM+Jsp+Mysql的农产品供销服务系统
开发语言:Java框架:ssm技术:JSPJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包…...

网络编程学习探索系列之——广播原理剖析
hello !大家好呀! 欢迎大家来到我的网络编程系列之广播原理剖析,在这篇文章中, 你将会学习到如何在网络编程中利用广播来与局域网内加入某个特定广播组的主机! 希望这篇文章能对你有所帮助,大家要是觉得我写…...

小程序开发SSL证书下载和安装
在开发小程序时,确保数据的安全传输至关重要,而实现这一目标的关键在于正确获取与安装SSL证书。以下详细介绍了从获取到安装SSL证书的完整流程,以助您为小程序构建可靠的加密通信环境。 一、小程序SSL证书类型选择: 域名验证型D…...

医疗图像分割 | 基于Pyramid-Vision-Transformer算法实现医疗息肉分割
项目应用场景 面向医疗图像息肉分割场景,项目采用 Pytorch Pyramid-Vision-Transformer 深度学习算法来实现。 项目效果 项目细节 > 具体参见项目 README.md (1) 模型架构 (2) 项目依赖,包括 python 3.8、pytorch 1.7.1、torchvision 0.8.2(3) 下载…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
