秒懂算法 | DP概述和常见DP面试题

动态(DP)是一种算法技术,它将大问题分解为更简单的子问题,对整体问题的最优解决方案取决于子问题的最优解决方案。本篇内容介绍了DP的概念和基本操作;DP的设计、方程推导、记忆化编码、递推编码、滚动数组以及常见的DP面试题。
01、DP概述
1. DP问题的特征
下面以斐波那契数为例说明DP的概念。斐波那契数列的每个数字是前面两个数字的和,前几个数是1、1、2、3、5、8。计算第n个斐波那契数,用递推公式进行计算:
fib(n) = fib(n-1) + fib(n-2)
用递归编程,代码如下。
int fib (int n){if (n == 1 || n == 2)return 1;return (fib (n -1) + fib (n -2));
}为了解决总体问题fib(n),将其分解为两个较小的子问题fib(n−1)和fib(n−2)。这就是DP的应用场景。
有一些问题有2个特征:重叠子问题、最优子结构。用DP可以高效率地处理具有这2个特征的问题。
(1)重叠子问题
首先,子问题是原大问题的小版本,计算步骤完全一样;其次,计算大问题的时候,需要多
相关文章:

秒懂算法 | DP概述和常见DP面试题
动态(DP)是一种算法技术,它将大问题分解为更简单的子问题,对整体问题的最优解决方案取决于子问题的最优解决方案。本篇内容介绍了DP的概念和基本操作;DP的设计、方程推导、记忆化编码、递推编码、滚动数组以及常见的DP面试题。 01、DP概述 1. DP问题的特征 下面以斐波那…...
)
【C++提高编程】C++全栈体系(二十五)
C提高编程 第四章 STL- 函数对象 一、函数对象 1. 函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象函数对象使用重载的()时,行为类似函数调用,也叫仿函数 本质: 函数对象(仿函数)是一个类&…...

【云原生】k8s核心技术—集群安全机制 Ingress Helm 持久化存储-20230222
文章目录一、k8s集群安全机制1. 概述2. RBAC——基于角色的访问控制二、Ingress三、Helm1. 引入2. 使用功能Helm可以解决哪些问题3. 介绍4. 3个重要概念5. helm 版本变化6. helm安装及配置仓库7. 使用helm快速部署应用8. 自己创建chart9. 实现yaml高效复用四、持久化存储1.nfs—…...
【Linux】实现简易的Shell命令行解释器
大家好我是沐曦希💕 文章目录一、前言二、准备工作1.输出提示符2.输入和获取命令3.shell运行原理4.内建命令5.替换三、整体代码一、前言 前面学到了进程创建,进程终止,进程等待,进程替换,那么通过这些来制作一个简易的…...

再获认可!腾讯安全NDR获Forrester权威推荐
近日,国际权威研究机构Forrester发布最新研究报告《The Network Analysis And Visibility Landscape, Q1 2023》(以下简称“NAV报告”),从网络分析和可视化(NAV)厂商规模、产品功能、市场占有率及重点案例等…...
代码审计之旅之百家CMS
前言 之前审计的CMS大多是利用工具,即Seay昆仑镜联动扫描出漏洞点,而后进行审计。感觉自己的能力仍与零无异,因此本次审计CMS绝大多数使用手动探测,即通过搜索危险函数的方式进行漏洞寻找,以此来提升审计能力…...
ONLYOFFICE中利用chatGPT帮助我们策划一场生日派对
近日,人工智能chatGPT聊天机器人爆火,在去年年底发布后,仅仅两个月就吸引了全球近一亿的用户,成为史上最快的应用消费程序,chatGPT拥有强大的学习和交互能力 可以被学生,教师,上班族各种职业运…...
)
Java面试题-线程(一)
在典型的 Java 面试中, 面试官会从线程的基本概念问起, 如:为什么你需要使用线程,如何创建线程,用什么方式创建线程比较好(比如:继承 thread 类还是调用 Runnable 接口),…...

一篇普通的bug日志——bug的尽头是next吗?
文章目录[bug 1] TypeError: method object is not subscriptable[bug 2] TypeError: unsupported format string passed to numpy.ndarray.__format__[bug 3] ValueError:Hint: Expected dtype() paddle::experimental::CppTypeToDataType<T>::Type()[bug 4] CondaSSLE…...

Vue 3 第八章:Watch侦听器
文章目录Watch侦听器1. 基础概念1.1. Watch的基本用法例子1:监听单个ref的值,直接监听例子2:监听多个ref的值,采用数组形式例子3:深度监听例子4:监听reactive响应式对象单一属性,采用回调函数的…...
GlassFish的安装与使用
一、产品下载与安装glassfish下载地址:https://download.oracle.com/glassfish/5.0.1/release/index.html下载后解压即完成安装,主要目录说明:bin目录:为asadmin命令所在目录。glassfish为主目录:glassfish\bin目录为命…...
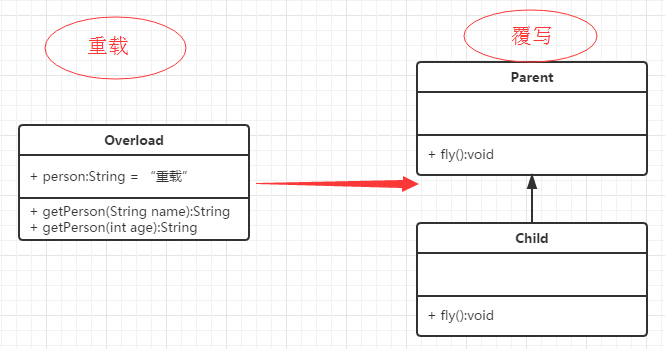
【java】Java 重写(Override)与重载(Overload)
文章目录重写(Override)方法的重写规则Super 关键字的使用重载(Overload)重载规则实例重写与重载之间的区别总结重写(Override) 重写是子类对父类的允许访问的方法的实现过程进行重新编写, 返回值和形参都不能改变。即外壳不变,核心重写! 重写的好处在于…...
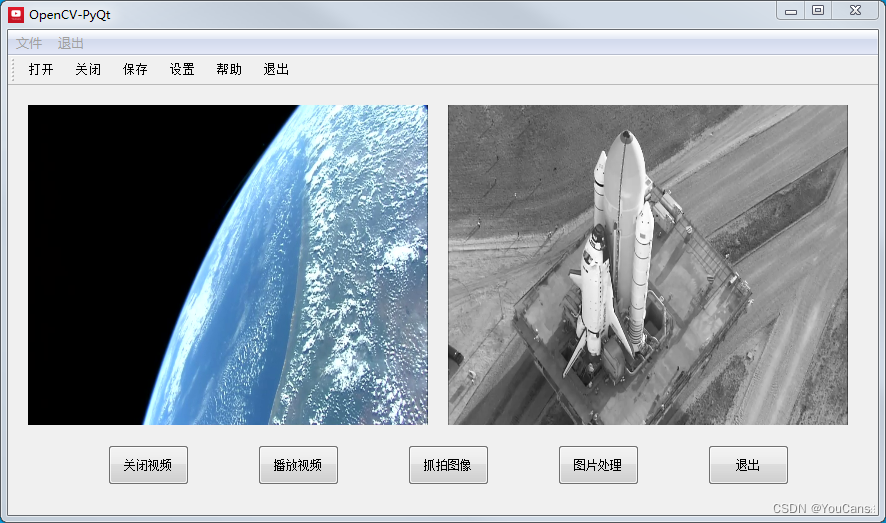
OpenCV-PyQT项目实战(12)项目案例08:多线程视频播放
欢迎关注『OpenCV-PyQT项目实战 Youcans』系列,持续更新中 OpenCV-PyQT项目实战(1)安装与环境配置 OpenCV-PyQT项目实战(2)QtDesigner 和 PyUIC 快速入门 OpenCV-PyQT项目实战(3)信号与槽机制 …...
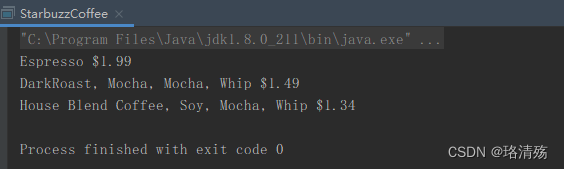
面向对象设计模式:结构型模式之装饰器模式
文章目录一、引入二、装饰器模式2.1 Intent 意图2.2 Applicability 适用性2.3 类图2.4 优缺点2.5 应用实例:Java IO 类2.6 应用实例:咖啡馆订购系统一、引入 咖啡馆订购系统 Initial 初始 4 种咖啡 House blend (混合咖啡)Dark Roast (深度烘培)Decaf (…...
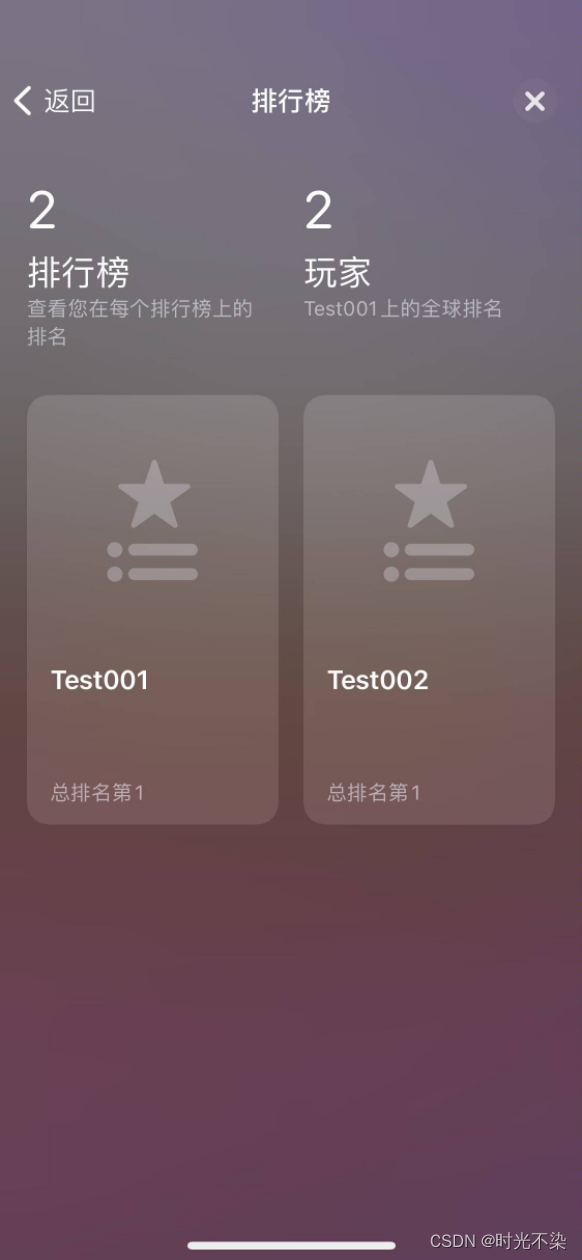
Unity iOS 无服务器做一个排行榜 GameCenter
排行榜需求解决方案一(嗯目前只有一)UnityEngine.SocialPlatformsiOS GameCenterAppStoreConnect配置Unity 调用(如果使用GameCenter系统的面板,看到这里就可以了)坑(需要获取数据做自定义面板的看这里)iOS代码Unity 代码吐槽需求 需求:接入…...

现在招个会自动化测试的人是真难呀~你会个锤子的自动化测试
现在招个会自动化测试的人是真难呀~ 前一段时间公司计划要招2个自动化测试到岗,同事面试了十几个来应聘的人,发现一个很奇怪的现象,在面试的时候,如果问的是框架API、脚本编写这些问题,基本上所有人都能对答如流&…...

OracleDatabase——数据库表空间dmp导出与导入
由于公司的程序一直部署在客户现场内网,内网调试难度高,一般是有备份还原数据库的需求,这里简记备份(导出)数据库dmp文件与恢复(导入)的步骤。 一、导出dmp文件 exp与expdp命令异同 相同点&a…...
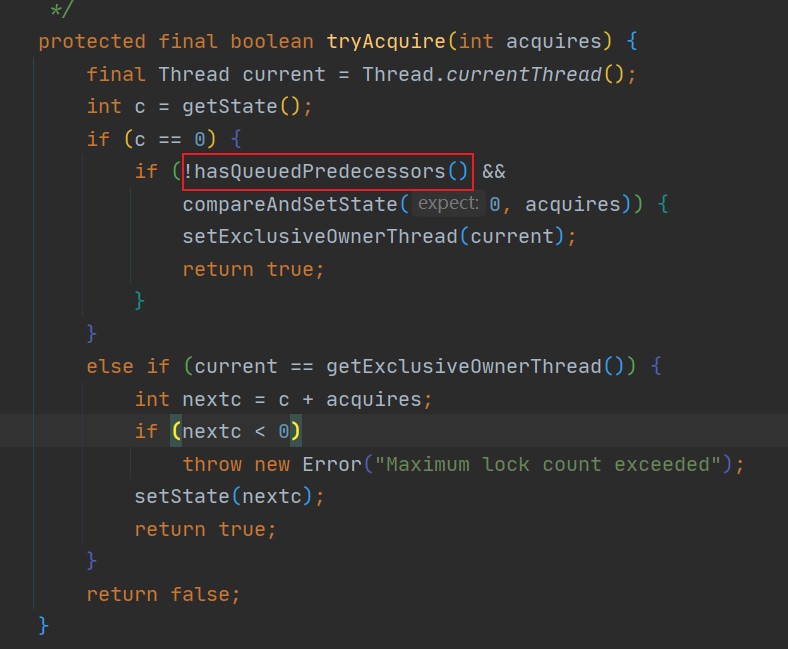
20张图带你彻底了解ReentrantLock加锁解锁的原理
哈喽大家好,我是阿Q。 最近是上班忙项目,下班带娃,忙的不可开交,连摸鱼的时间都没有了。今天趁假期用图解的方式从源码角度给大家说一下ReentrantLock加锁解锁的全过程。系好安全带,发车了。 简单使用 在聊它的源码…...

Dockerfile构建Springboot镜像
Dockerfile构建Springboot镜像 文章目录 Dockerfile构建Springboot镜像 简介实例演示 前期准备 Docker环境Springboot项目Dockerfile文件 Windows 要求构建镜像启动测试 Linux 要求构建镜像启动测试 简介 容器技术大流行的时代,也是docker大流行的时代。 此文…...

从深分页查询到覆盖索引
最近看到一道面试题,如何优化深分页查询 最简单的例子是 select * from web_bill_main limit 30000,10;分页达到30000行,需要把前面29999行都过滤掉,才能找到这10条数据 所以整体时间花了80ms(工具显示时间) 我当时的第一反应是࿰…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
