[matlab]matcaffe在matlab2023a安装和配置过程
测试环境:
caffe-windows-cpu-py35-matlab2018b-vs2015-20220321
matlab2023a
注意:由于matlab新版本不允许添加特殊目录,比如有+和private目录,添加后也会警告,但是可以忽略。因此可以使用我研发的matlab环境添加工具进行添加操作或者手动编辑D:\Program Files\MATLAB\R2023a\toolbox\local\pathdef.m文件。
步骤:
将bin文件夹加入用户环境变量或者系统环境变量path
C:\Users\Administrator\Desktop\caffe-windows\build\install\bin
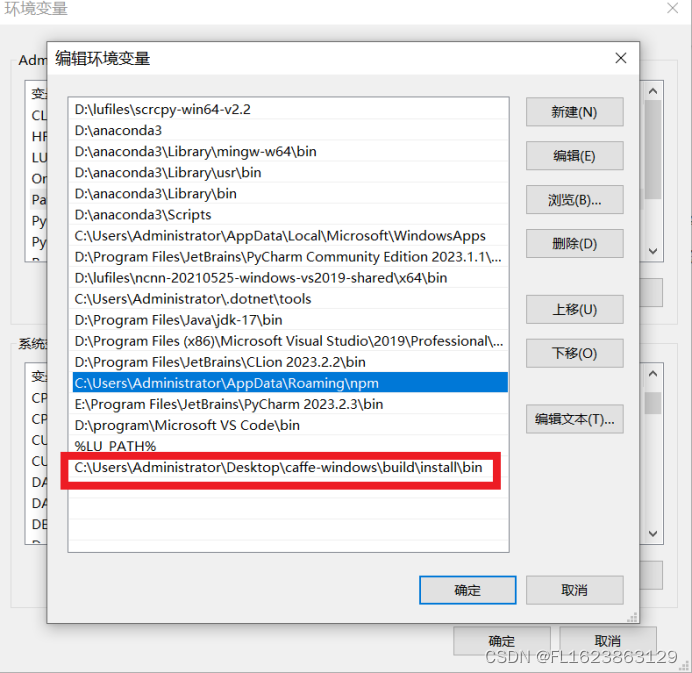
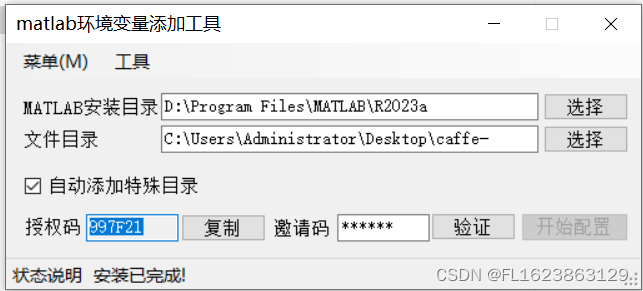
使用添加环境变量工具添加caffe目录:
添加目录是C:\Users\Administrator\Desktop\caffe-windows\build\install\matlab\+caffe
注意添加完要重启matlab,我们打开matlab选择C:\Users\Administrator\Desktop\caffe-windows\matlab\demo目录
将synset_words.txt
放入C:\Users\Administrator\Desktop\caffe-windows\matlab\demo
将bvlc_reference_caffenet.caffemodel
放入C:\Users\Administrator\Desktop\caffe-windows\models\bvlc_reference_caffenet
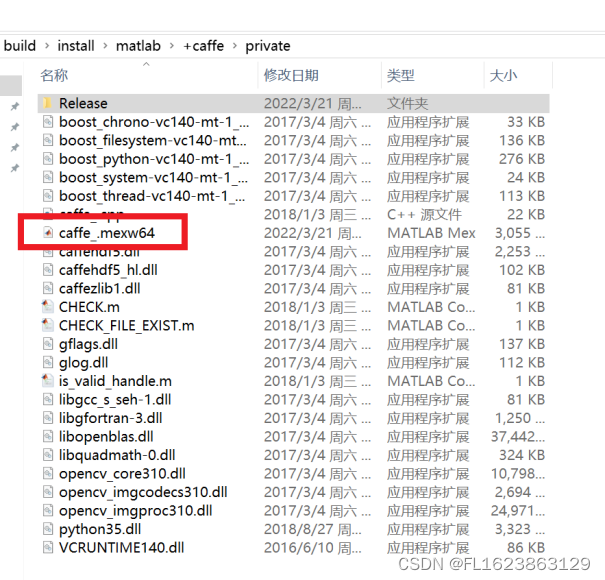
将C:\Users\Administrator\Desktop\caffe-windows\build\install\matlab\+caffe\private\Release里面的caffe_.mexw64放到上一级目录中即
C:\Users\Administrator\Desktop\caffe-windows\build\install\matlab\+caffe\private
打开classification_demo.m,修改60行为
addpath('../../build/install/matlab');
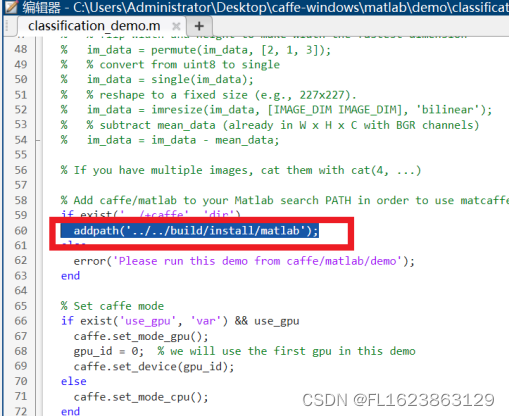
此时报错:
错误使用 caffe_
Could not convert handle to pointer due to invalid init_key. The object might have been cleared.
出错 caffe.Net/delete (第 73 行)
caffe_('delete_net', self.hNet_self);
出错 classification_demo (第 114 行)
caffe.reset_all();
> 位置:classification_demo (第 114 行)
解决方法为修改2处Net.m代码,安装目录有个+caffe目录
C:\Users\Administrator\Desktop\caffe-windows\build\install\matlab\+caffe
C:\Users\Administrator\Desktop\caffe-windows\matlab\+caffe
需要修改:caffe-windows\matlab\+caffe\Net.m,第72行:
将:
function delete (self)
if ~isempty(self.hNet_self)
caffe_('delete_net', self.hNet_self);
end
end
改成
function delete (self)
if self.isvalid
caffe_('delete_net', self.hNet_self);
end
end
再次运行即可成功。
相关文章:

[matlab]matcaffe在matlab2023a安装和配置过程
测试环境: caffe-windows-cpu-py35-matlab2018b-vs2015-20220321 matlab2023a 注意:由于matlab新版本不允许添加特殊目录,比如有和private目录,添加后也会警告,但是可以忽略。因此可以使用我研发的matlab环境添加工具…...

【word2pdf】Springboot word转pdf(自学使用)
文章目录 概要整体介绍具体实现官网pom文件增加依赖 遇到的问题本地运行OK,发布到Linux报错还是本地OK,但是Linux能运行的,但是中文乱码 小结 概要 Springboot word 转 pdf 整体介绍 搜了一下,发现了能实现功能的方法有四种 U…...
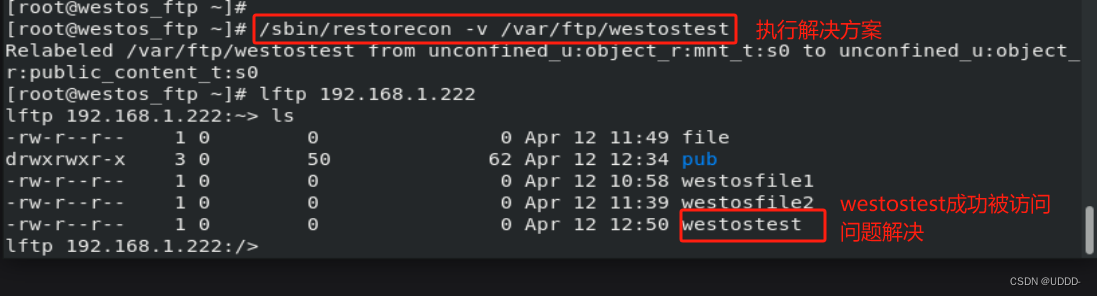
3_2Linux中内核级加强型火墙的管理
### 一.Selinux的功能 ### 观察现象 ①当Selinux未开启时 在/mnt中建立文件被移动到/var/ftp下可以被vsftpd服务访问 匿名用户可以通过设置后上传文件 当使用ls -Z /var/ftp查看文件时显示"?" ps auxZ | grep vsftpd 时显示: - root 8546 0.0 0.0 26952 …...

PCB工艺规范及PCB设计安规原则
一、目的 规范产品的PCB工艺设计,规定PCB工艺设计的相关参数,使得PCB的设计满足可生产性、可测试性、安规、EMC、EMI等的技术规范要求,在产品设计过程中构建产品的工艺、技术、质量、成本优势。 二、适用范围 本规范适用于所有电了产品的PCB工…...
Qt for Android 开发环境
在搭建环境时开始感觉还挺顺利的,从 Qt 配置的环境里面看并没有什么问题,可真正编译程序的时候发现全是错误。 最开始的时候安装了 JDK21 最新版本,然后根据 JDK21 安装 ndk, build-tools, Platform-Tools 和 Gradle,但是不管这么…...
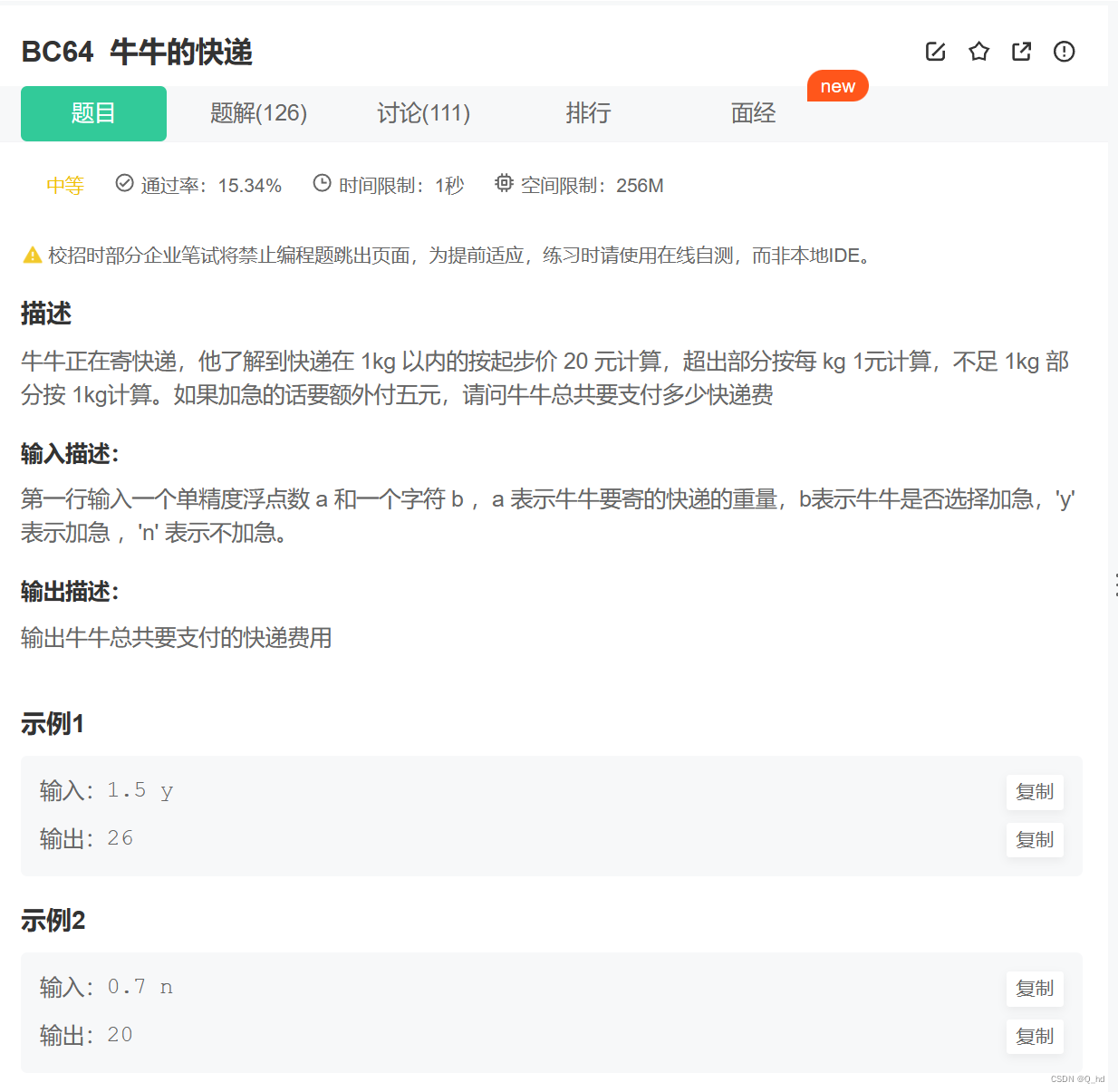
【题解】BC64 牛牛的快递(C++)
#include <iostream> #include<string> #include<math.h> using namespace std;int main() {int c0;string b;float a;cin>>a>>b;if(a>1)c20ceil(a-1);elsec20;if(b"y")c5;cout<<c; }在C中,ceil() 函数用于返回大…...

C++(运算符重载+赋值拷贝函数+日期类的书写)
目录 运算符重载运算赋值重载和运算赋重载前置和后置<,<,>,>,,!运算符重载日期类的实现<<流插入和>>流提取的运算符重载总结 运算符重载 C为了增强代码的可读性引入了运算符重载,运算符重载是具有特殊函数名的函数,也具有其 返回…...

【介绍下负载均衡原理及算法】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

CESS 受邀出席香港Web3.0标准化协会第一次理事会议,共商行业未来
2024 年 4 月 5 日,CESS(Cumulus Encrypted Storage System)作为香港 Web3.0 标准化协会的副理事会成员,于香港出席了 2024 年度第一次理事会会议。此次会议汇聚了来自不同领域的知名企业和专家(参会代表名单见文末&am…...
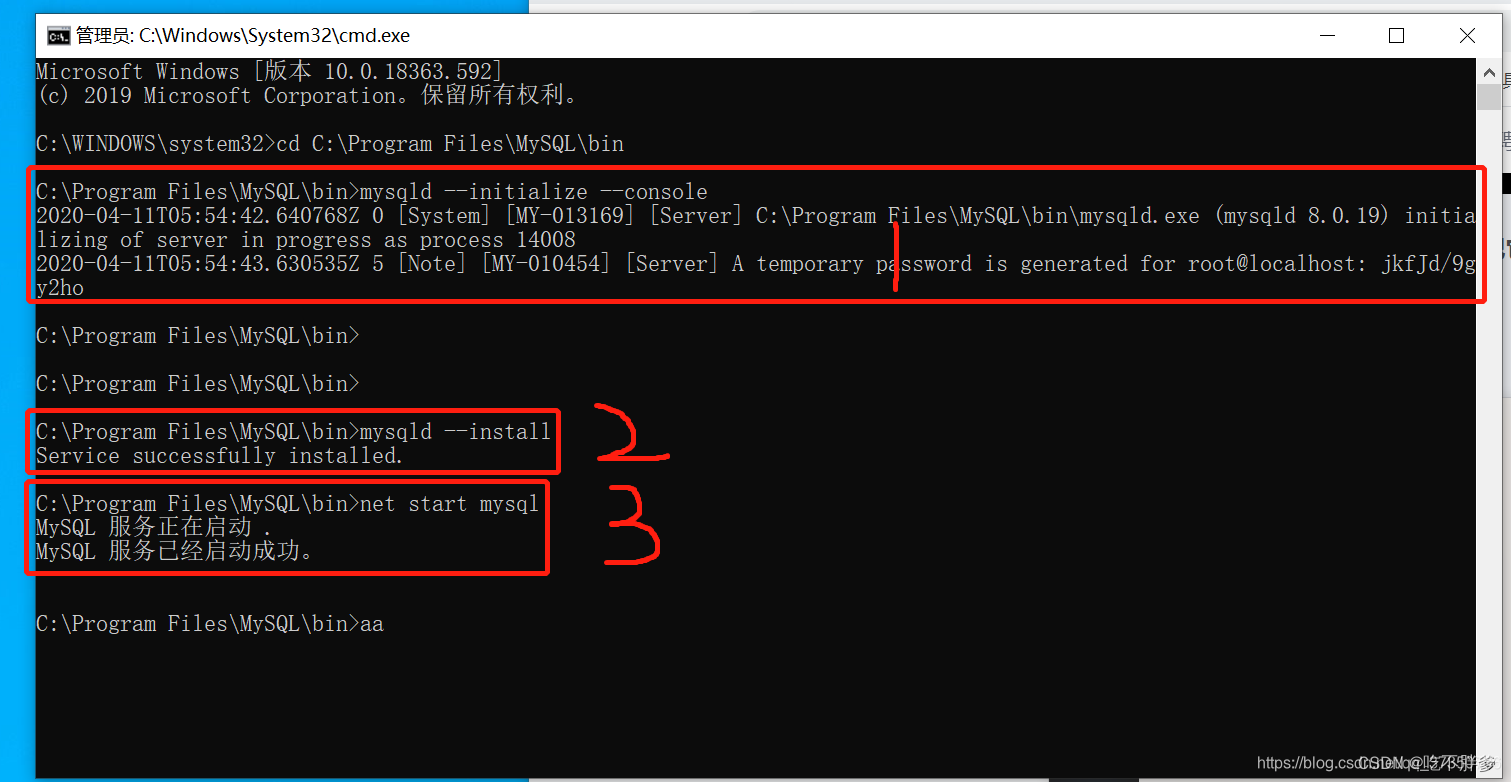
MySQL 8.0.19安装教程(windows 64位)
在c盘目录下的Program Files目录下创建MySQL目录,将下载好的mysql解压到里面 解压完是这个样子 配置初始化的my.ini文件的文件 [mysqld] # 设置3306端口 port3306 # 设置mysql的安装目录 basedirC:\Program Files\MySQL # 设置mysql数据库的数据的存放目录 datad…...
探索AI提示词网站:助力内容创作与AI对话
嗨,大家好!在这个充满创意的时代里,AI技术为我们带来了许多惊喜和便利。如果你是一个内容创作者,无论是在撰写博客还是进行科技对话,今天我将向大家介绍几个能够提升与AI对话效率的神奇网站。 1. FlowGPT 首先…...

AdaBoost 算法
目录 什么是 AdaBoost 算法? Adaboost 的 7 个优缺点 集成学习:人多力量大: Bagging:民主。Boosting :挑选精英。长短期记忆网络:引入遗忘机制 生成对抗网络 :物竞天择适者生存 首先,了解一下集成学习及 Boosting 算法 集成学习归属于机器学习,他是一种「训练思路…...

链接分析算法
链接分析(Link Analysis)通常指的是对图(Graph)中的节点(Nodes)和边(Edges)进行分析,以发现图的结构和属性。在图论中,链接分析算法通常用于解决诸如网页排名…...

怎么批量完成图片格式转换?介绍三种简单方法
在日常生活和工作中,我们经常会遇到需要将图片格式转换的情况,无论是为了适应不同的设备要求,还是为了能让我们的图片应用到更多的使用场景中去,批量图片格式转换都是一项非常实用的技能。本文将介绍一些常见的批量图片格式转换方…...
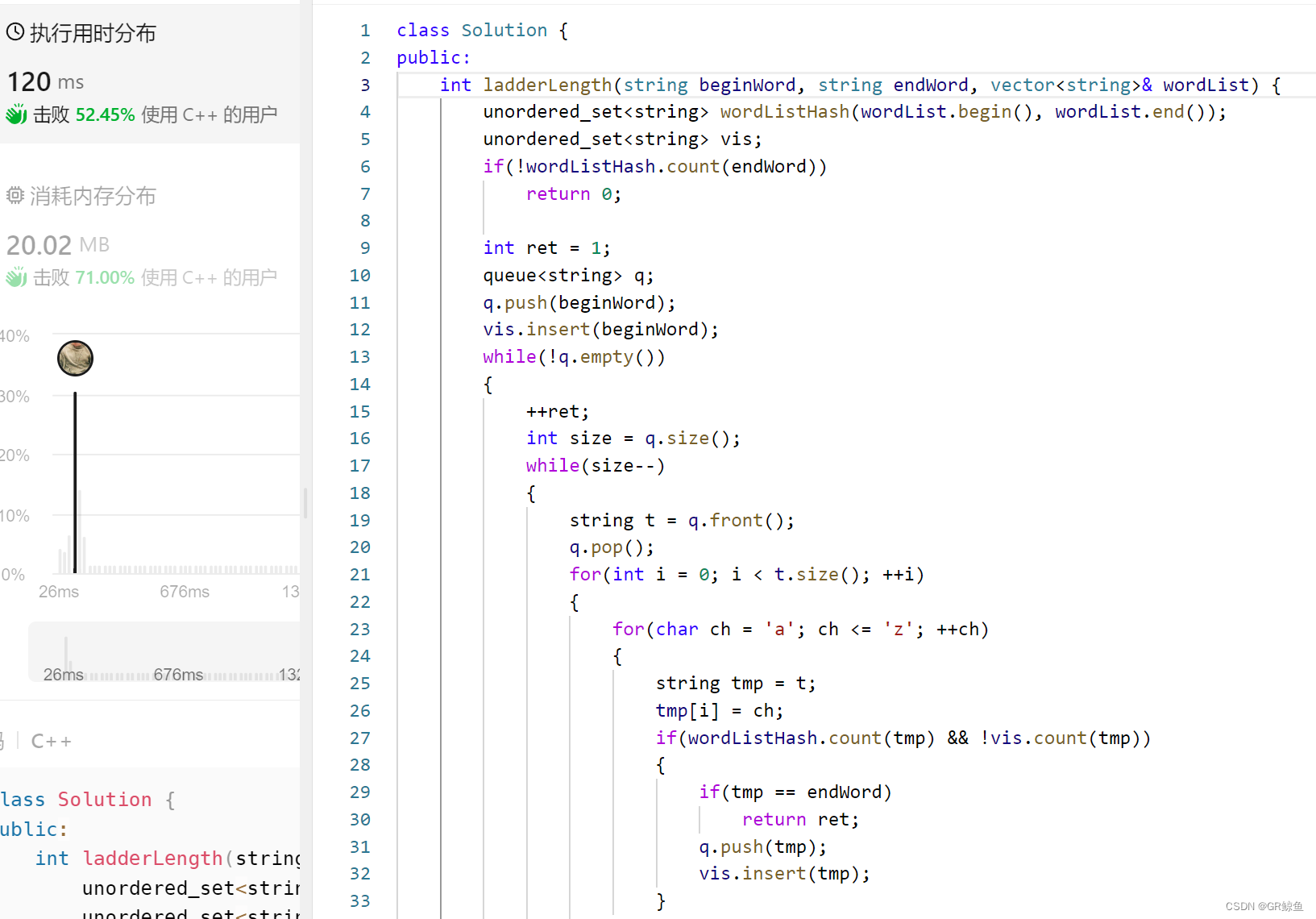
每日OJ题_BFS解决最短路③_力扣127. 单词接龙
目录 ③力扣127. 单词接龙 解析代码 ③力扣127. 单词接龙 127. 单词接龙 难度 困难 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk: 每一对相邻的单词只差一个字母。…...
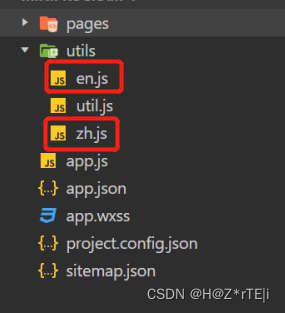
微信小程序英文版:实现一键切换中英双语版(已组件化)
已经重新优化代码做成了组件,需要可自取:https://github.com/CrystalCAI11/wechat-language-compoment 所有操作都打包在组件里不需要在额外的地方添加代码,直接在你需要的页面里导入组件,再在对应页面的onLoad()里set文本就行了。…...

openstack之neutron介绍
核心组件 neutron-server:提供API接口,把对应的api请求传给plugin进; neutron-plugin:管理逻辑网络状态,调用agent; neutron-agent:在provider network上创建网络对象; neutron-…...

学习Rust的第三天:猜谜游戏
基于Steve Klabnik的《The Rust Programming Language》一书。今天我们在rust中建立一个猜谜游戏。 Introduction 介绍 We will build a game that will pick a random number between 1 to 100 and the user has to guess the number on a correct guess the user wins. 我们将…...

React中子传父的方式及原理
方式挺多的,先说最常用的通过props进行父子组件的数据传递和修改以及原理 在React中,props不仅用于传递数据,它们也可以传递可以执行的函数,这使得子组件能够间接更新父组件的状态。这种方法强化了React的单向数据流策略…...
【数据结构与算法】贪心算法及例题
目录 贪心算法例题一:找零问题例题二:走廊搬运物品最优方案问题输入样例例题三:贪心自助餐 贪心算法 贪心算法是一种在每一步选择中都采取当前状态下最优的选择,以期望最终达到全局最优解的算法。它的核心思想是每次都选择当前最…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
