密码学 | 椭圆曲线数字签名方法 ECDSA(下)
目录
10 ECDSA 算法
11 创建签名
12 验证签名
13 ECDSA 的安全性
14 随机 k 值的重要性
15 结语
⚠️ 原文:Understanding How ECDSA Protects Your Data.
⚠️ 写在前面:本文属于搬运博客,自己留着学习。同时,经过几天的折磨后,我对椭圆曲线已经有点基础了,因此删除了一些我认为无关紧要的原文。
10 ECDSA 算法
现在让我们来谈谈 ECDSA 签名算法。
对于 ECDSA,你首先需要知道你的曲线参数,即 a、b、p、N 和 G。你已经知道 a 和 b 是曲线函数的参数:
还知道 p 是模数,N 是曲线的点数。但还需要知道 G 是什么。G 代表一个 “参考点” 或者说一个 “原点”,参考点可以是曲线上的任何一点。
NIST(美国国家标准与技术研究院)和 SECG(高效加密标准组)提供了预先制作和标准化的曲线参数,这些参数被认为是有保障且高效的。
私钥是一个 160 位的随机数,而公钥是曲线上的一个点,它是私钥与参考点 G 的点乘结果。设 dA 为私钥,Qa 为公钥,则有:Qa = dA * G,其中 G 是曲线参数中的参考点。
不懂 dA 和 Qa 为什么要这样大小写 😇
11 创建签名
一个签名的长度是 40 个字节,它由两个 20 字节的值组成,第一个称为 R,第二个称为 S,所以 (R, S) 共同构成 ECDSA 签名。具体流程如下:
首先,您必须生成一个随机值 k(20 字节),并使用 “点乘法” 计算 P 点:
P 点的 x 坐标值即为 R,它的长度是 20 个字节。
为了计算 S,您必须对消息进行 SHA1 散列,得到一个长为 20 个字节的值,我们将称之为 z 。现在您可以使用以下方程计算 S:
请注意 k^{-1},它是 k 的 “模乘逆”。虽然 k^{-1} 本质上是 k 的倒数,但由于我们处理的是整数,所以这是不可能的。因此要求 k^{-1} 是一个整数,它能够使得 (k^{-1} * k) mod p 等于 1 。
暂时还没有学 “模乘逆”,应该就是一个求模数的方法。
再次提醒您,k 是用于生成 R 的随机数,z 是要被签署的消息的散列,dA 是私钥,R 是 k*G 的 x 坐标值,其中 G 是曲线参数的参考点。
12 验证签名
既然您已经有了签名,您想要验证它,这也是相当简单的。
您使用这个方程来计算一个点 P:
只要 P 点的 x 坐标值等于 R,就意味着签名是有效的,否则它就不是。
按照上述方程把 P 点计算出来,只要这个 P 点的 x 坐标值等于 R,就说明签名有效。
很简单,对吧?现在让我们看看为什么成立,这需要一些数学来验证。
我们有:
可以看出,算 P 点的时候只需要使用一些公开的数据,而不会涉及私钥。
其中
因此
我们代入 P 点的坐标值有:
我们可以通过消除 G 来简化,得到:
通过求 k 和 S 的逆,我们得到:
这正是用于生成签名的方程,因此等号左右两边的式子是相等的。这就是为什么您可以使用上面的第一个方程来验证签名。
签名的时候会需要使用私钥 dA,验证的时候只需要使用公钥 Qa,这就是所谓的零知识证明吧。
13 ECDSA 的安全性
因为 Qa=dA*G、P=k*G,又因为 ECDSA 的 “点乘法” 是一个陷门函数 —— 在第 9 步中解释过 —— 所以我们不能根据 Qa 和 P 来倒推 dA 或 k,这使得 ECDSA 算法是安全的。
我们没有办法找到私钥,也没有办法在不知道私钥的情况下伪造签名。
为什么 “也没有办法在不知道私钥的情况下伪造签名”?
14 随机 k 值的重要性
现在让我们讨论一下索尼在 Playstation 3 上使用的 ECDSA 签名是如何出现缺陷的,以及这是如何允许黑客获取 PS3 的 ECDSA 私钥的。
生成签名所需的方程如下:
S 方程的强度在于它一个方程含有两个未知数,即 k 和 dA,因此无法进行求解。
然而,算法的安全性基于其实现,即确保 “k 是随机生成的” 非常重要,确保没有任何人能够猜测、计算,或者使用时序攻击或其他任何类型的攻击来找到随机值 k 。
索尼
但是索尼在实现上犯了一个巨大的错误,他们在任何地方都使用相同的 k 值。
这意味着如果你有两个签名,它们都有相同的 k,那么它们都会有相同的 R 值。同时这意味着,只要你拥有同一个人的两个签名 S 和 S',就能计算出 k 值。
首先让 S 和 S' 相减:
整理得到
从而有
其中,z 和 z'、S 和 S' 都是已知的。
一旦得到了 k,那么 S 方程就只含一个未知数了,从而可以很容易地解出 dA:
一旦得到了私钥 dA,你可以用它来签署自己的文件,而 PS3 将会认为它是索尼签名的合法文件。这就是为什么确保用于生成签名的随机数实际上是 “密码学上随机” 的非常重要的原因。
比特币
另一个例子是当一些比特币客户端在某些浏览器和某些 Android 客户端上使用非密码学随机数生成器时,这导致它们用相同的 k 值签署交易,恶意人士能够找到他们的比特币钱包私钥并盗取他们的资金。
小结
这显示了每次制作签名时使用真正随机数的重要性,因为如果你签名对的 (R, S) 中的 R 值在两个不同的签名中相同,你就会暴露私钥。
理论上,ECDSA 算法非常安全,不可能找到私钥。当然,它的前提是 “算法实现是正确的”。如果有一种方法可以找到私钥,那么每个计算机、网站、系统的安全性都可能受到威胁。
15 结语
最后!我希望这能让很多人更清楚地理解这个算法。我知道这仍然非常复杂和难以理解。我通常试图让非技术人士更容易理解事物,但这个算法太复杂了,无法用更简单的术语来解释。
但是,如果您是一名开发人员或数学家,或者您对学习此内容感兴趣,因为您想帮助或简单地获取知识,那么我相信这为您提供了开始学习或至少理解这个被称为 “ECDSA” 的未知野兽的概念的信息。
附言:在本文中,我使用了 “160位” 来讨论 ECDSA 签名,因为它通常与 160 位的 SHA1 散列值(20 字节)匹配,而且 PS3 安全机制就是使用的这种组合。但是,该算法本身可以使用任何大小的数字。本文可能存在其他不准确之处,但就像我说的,我不是专家,而且我已经尽可能地将内容简化,同时没有删除关于算法的任何信息。
相关文章:
密码学 | 椭圆曲线数字签名方法 ECDSA(下)
目录 10 ECDSA 算法 11 创建签名 12 验证签名 13 ECDSA 的安全性 14 随机 k 值的重要性 15 结语 ⚠️ 原文:Understanding How ECDSA Protects Your Data. ⚠️ 写在前面:本文属于搬运博客,自己留着学习。同时,经过几…...
拟态个人主页UI源码
拟态个人主页 效果图源代码领取源码 效果图 PC端 移动端 源代码 index.php <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>孤客 |佩恩</title><meta name"keywords" co…...

移动硬盘无法打开?别慌!这里有救星!
移动硬盘作为现代生活中重要的数据存储工具,承载着我们大量的文件和数据。然而,有时我们会遇到移动硬盘无法打开的情况,这往往让人焦虑不已。那么,当移动硬盘无法打开时,我们应该如何应对呢? 移动硬盘无法打…...
windows下已经创建好了虚拟环境,但是切换不了的解决方法
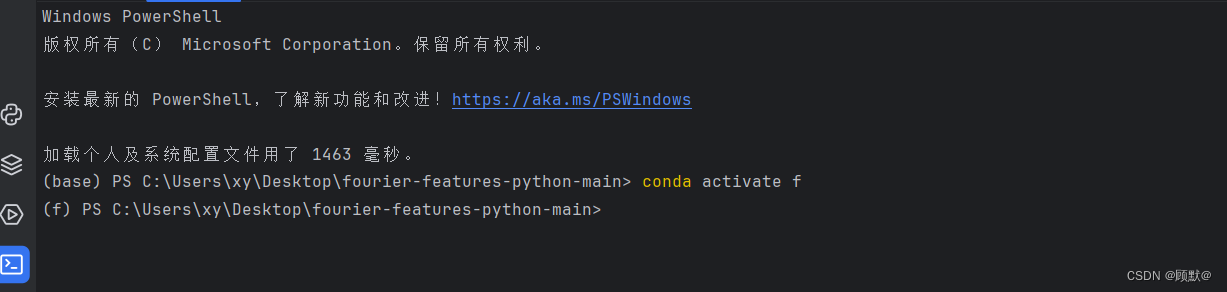
用得多Ubuntu,今天用Windows重新更新anaconda出问题,重新安装之后,打开pycharm发现打开终端之后,刚开始是ps的状态,后面试了网上改cmd的方法,终端变成c盘开头了 切换到虚拟环境如下:目前的shell…...
Java反序列化基础-类的动态加载
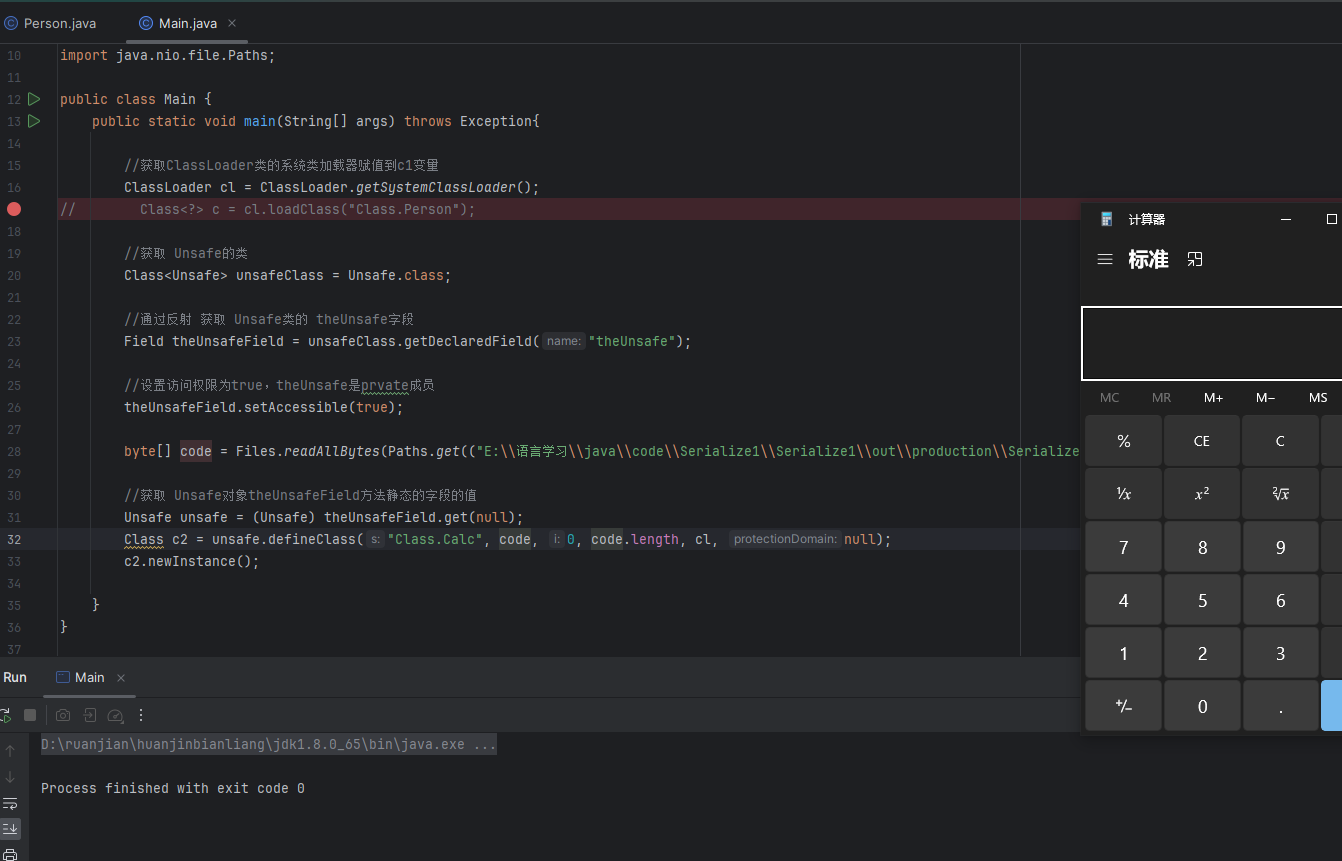
类加载器&双亲委派 什么是类加载器 类加载器是一个负责加载器类的对象,用于实现类加载的过程中的加载这一步。每个Java类都有一个引用指向加载它的ClassLoader。而数组类是由JVM直接生成的(数组类没有对应的二进制字节流) 类加载器有哪…...

课堂行为动作识别数据集
一共8884张图片 xml .txt格式都有 Yolo可直接训练 已跑通 动作类别一共8类。 全部为教室监控真实照片,没有网络爬虫滥竽充数的图片,可直接用来训练。以上图片均一一手工标注,标签格式为VOC格式。适用于YOLO算法、SSD算法等各种目标检测算法…...

【数据库】MVCC
MVCC是一种用来解决读写冲突的无锁并发控制,也就是为事务分配单项增长的时间戳,为每个修改保存一个版本,版本与事务时间戳关联,读操作只读该事务开始前的数据库的快照 MVCC,全称Multi-Version Concurrency Control&am…...

快速排序题目SelectK问题
力扣75.颜色分类 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在不使用库内置的 sor…...

es6解构赋值
ES6解构赋值是一种简洁的为变量赋值的方式,它允许我们从数组或对象中提取值并赋给对应的变量。 解构赋值在ES6中被引入,主要目的是为了简化代码,提高代码的可读性。以下是解构赋值的基本用法: 数组解构:当我们需要从数…...
Jenkins上面使用pnpm打包
问题 前端也想用Jenkins的CI/CD工作流。 步骤 Jenkins安装NodeJS插件 安装完成,记得重启Jenkins。 全局配置nodejs Jenksinfile pipeline {agent anytools {nodejs "18.15.0"}stages {stage(Check tool version) {steps {sh node -vnpm -vnpm config…...

设计编程网站集:动物,昆虫,蚂蚁养殖笔记
入门指南 区分白蚁与蚂蚁 日常生活中,人们常常会把白蚁与蚂蚁搞混淆,其实这两者是有很大区别的,养殖方式差别也很大。白蚁主要食用木质纤维,会给家庭房屋带来较大危害,而蚂蚁主要采食甜食和蛋白质类食物,不…...
)
面经学习(众智宏图实习)
个人评价 难度还是有的,中等难度吧,可能是因为项目使用的是物流项目,该项目本来就比较庞大难度比较高,流的八股文我真的是一点不会,还需要加强,reidis的多路io复用模型没有深问,要是问了就寄了&…...

DataGrip2024安装包(亲测可用)
目录 一、软件简介 二、软件下载 一、软件简介 DataGrip是由JetBrains公司开发的一款强大的关系数据库集成开发环境(IDE),专为数据库开发人员和数据库管理员设计。它提供了一个统一的界面,用于管理和开发各种关系型数据库&#x…...
【InternLM 实战营第二期-笔记4】XTuner 微调个人小助手认知
书生浦语是上海人工智能实验室和商汤科技联合研发的一款大模型,很高兴能参与本次第二期训练营,我也将会通过笔记博客的方式记录学习的过程与遇到的问题,并为代码添加注释,希望可以帮助到你们。 记得点赞哟(๑ゝω╹๑) XTuner 微调个人小助手…...
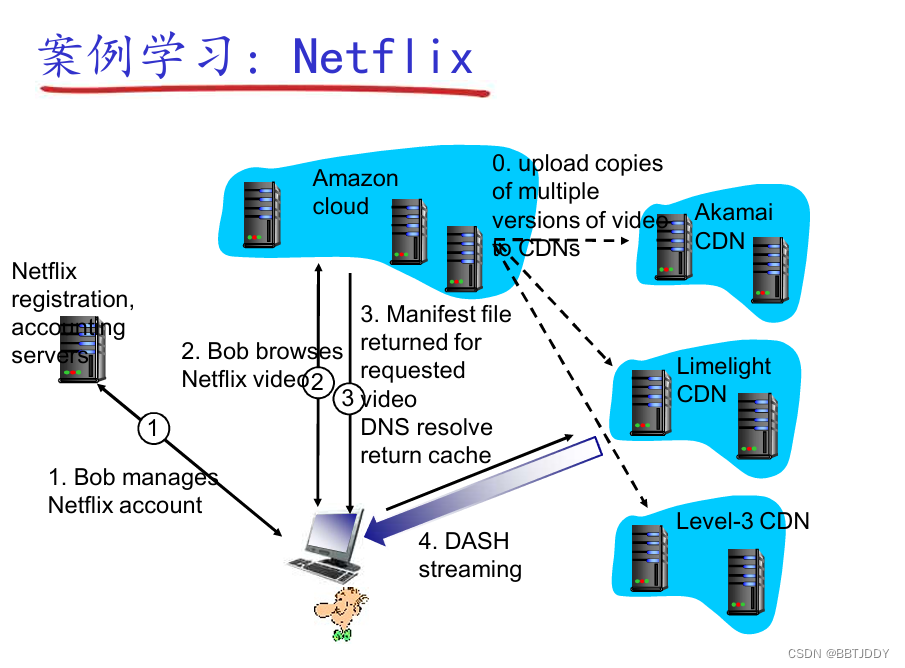
<计算机网络自顶向下> CDN
视频服务挑战 规模性异构性:不同用户有不同的能力(比如有线接入和移动用户;贷款丰富和受限用户)解决方法是:分布式的应用层面的基础设施CDN 多媒体:视频 视频是固定速度显示的一系列图像的序列ÿ…...

【Git教程】(十二)工作流之项目设置 — 何时使用工作流,工作流的结构,项目设置概述、执行过程及其实现 ~
Git教程 工作流之项目设置 1️⃣ 何时使用工作流2️⃣ 工作流的结构3️⃣ 概述4️⃣ 使用要求5️⃣ 执行过程及其实现5.1 基于项目目录创建一个新的版本库5.2 以文件访问的方式共享版本库5.3 用 Git daemon 来共享版本库5.4 用 HTTP 协议来共享版本库5.5 用 SSH 协议来共享版…...

Java 排序算法
冒泡排序 冒泡排序(Bubble Sort)是一种简单的排序算法,它通过重复地遍历要排序的数列,比较相邻元素的大小并交换位置,使得较大的元素逐渐向数列的末尾移动。 以下是Java实现的冒泡排序代码: public stat…...
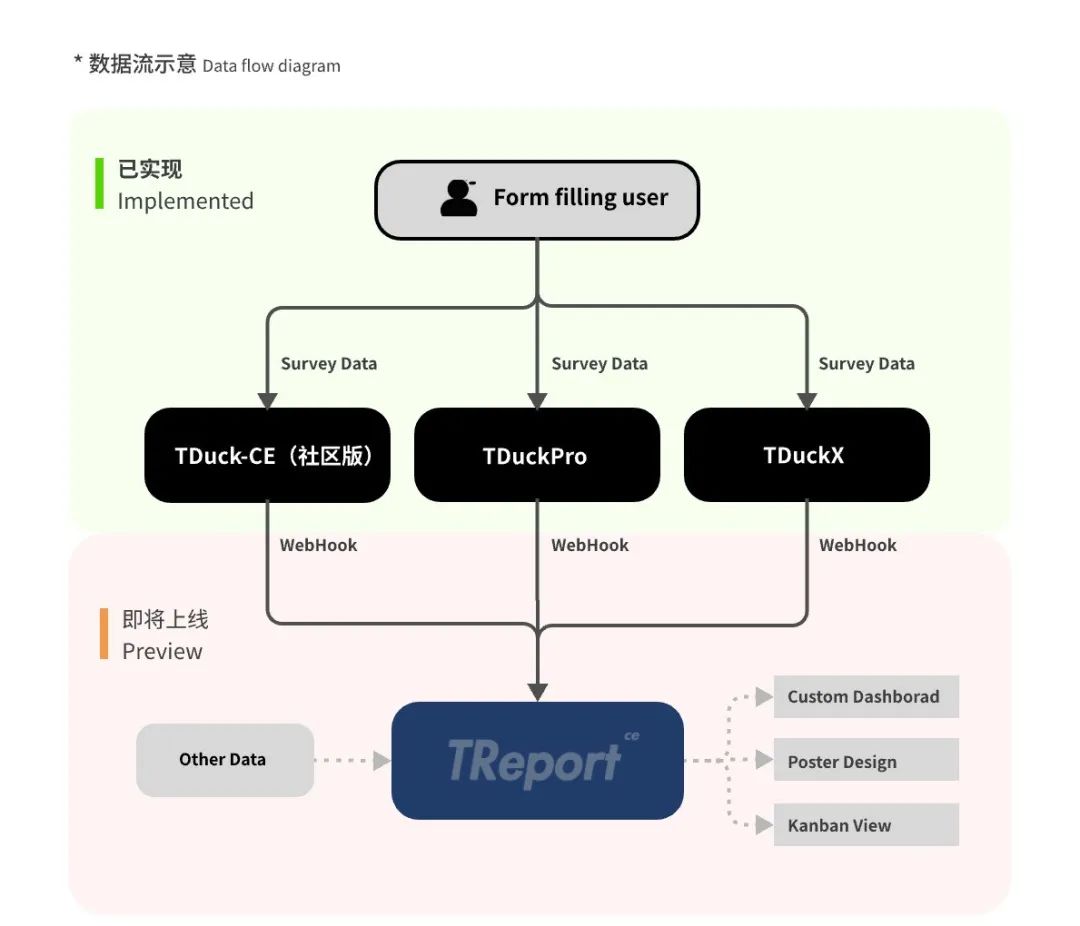
【重磅更新】开源表单系统填鸭表单v5版发布!
亲爱的TDucker,你们好。 真诚感谢您对填鸭表单的关注与支持。今天我们将为您带来新版本的更新说明,以便您更好的使用我们的产品。 社区版版V5更新概览: ✅ 增加WebHook数据推送功能,集成TReport实现数据大屏展示。 ✅ 增加主题…...
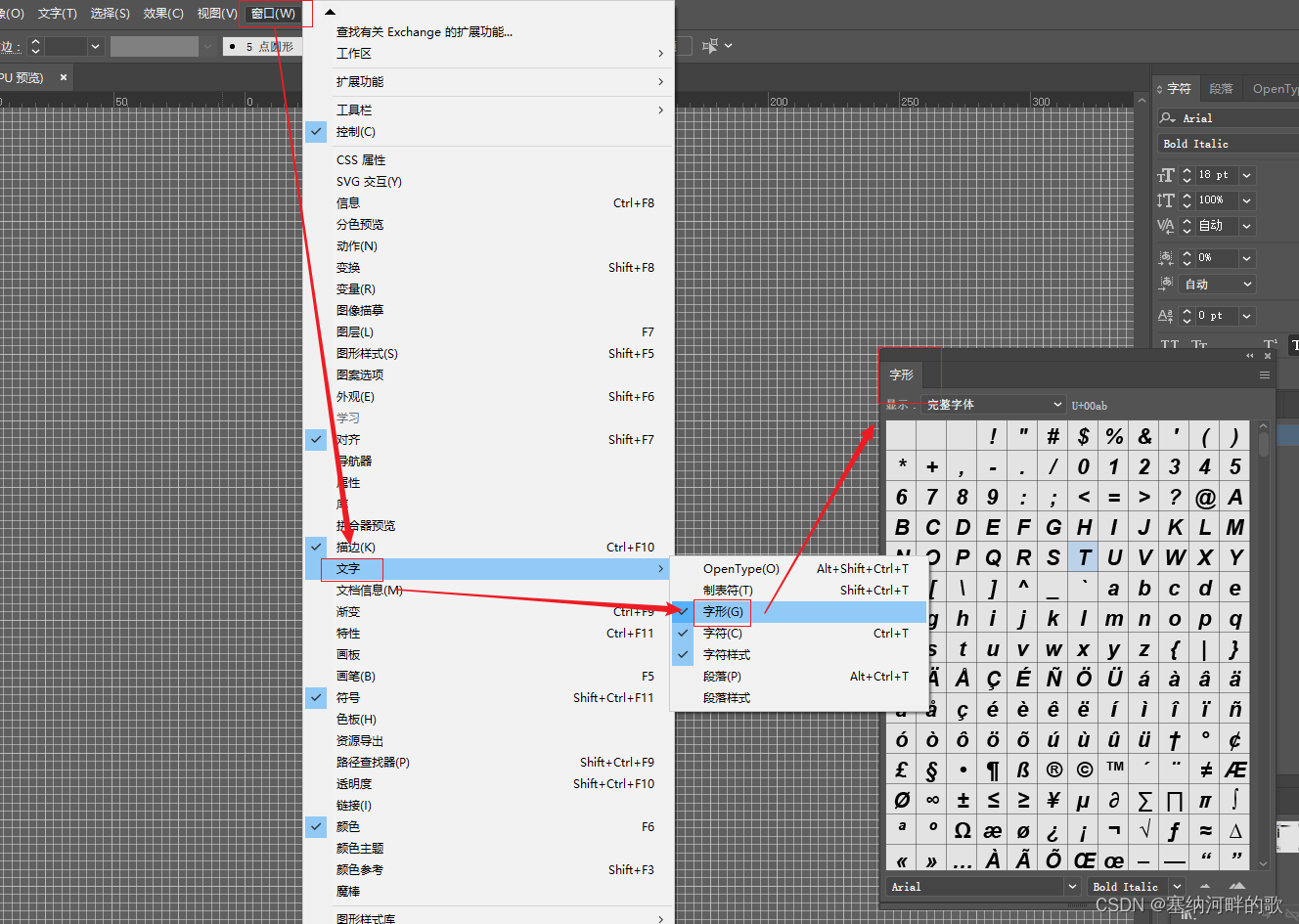
保姆级教程 | Adobe Illustrator 中插入数学符号
背景 鉴于Adobe Illustrator作为比较专业的绘图/组图软件,我的论文数据作图都会选择先在origin中把原始数据绘制好,后都放入AI中细修。由于在作图过程中需要插入数学符号,但仿佛没有PowerPoint用起来那么熟悉,遂记录下。 步骤 …...
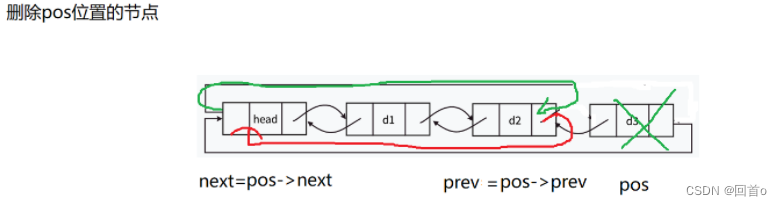
数据结构——双向循环链表
目录 前言 一、链表的分类 二、双向循环链表 2.1 开辟新的节点 2.2 链表初始化 2.3 打印链表 2.4 链表的尾插 2.5 链表的头插 2.6 链表的尾删 2.7 链表的头删 2.8 查找链表 2.9 在pos位置之后插入数据 2.10 删除pos位置的数据 三、完整代码实现 四、顺序表和双向…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...
