Python SQL解析和转换库之sqlglot使用详解
概要
Python SQLGlot是一个基于Python的SQL解析和转换库,可以帮助开发者更加灵活地处理和操作SQL语句。本文将介绍SQLGlot库的安装、特性、基本功能、高级功能、实际应用场景等方面。
安装
安装SQLGlot库非常简单,可以使用pip命令进行安装:
pip install sqlglot
安装完成后,即可开始使用SQLGlot库进行SQL语句的解析和转换。
特性
-
SQL语句解析:可以将SQL语句解析为语法树,便于后续的操作和分析。
-
SQL语句转换:可以对SQL语句进行转换,包括格式化、优化等操作。
-
支持多种数据库:可以处理多种数据库的SQL语句,如MySQL、PostgreSQL等。
基本功能
1. SQL语句解析
Python SQLGlot库可以将SQL语句解析为语法树,方便开发者理解和操作SQL语句的结构。
from sqlglot import parsesql = "SELECT * FROM users WHERE age > 30"
tree = parse(sql)print(tree)
2. SQL语句转换
SQLGlot库还可以对SQL语句进行转换,如格式化、优化等操作,提高SQL语句的可读性和性能。
相关文章:

Python SQL解析和转换库之sqlglot使用详解
概要 Python SQLGlot是一个基于Python的SQL解析和转换库,可以帮助开发者更加灵活地处理和操作SQL语句。本文将介绍SQLGlot库的安装、特性、基本功能、高级功能、实际应用场景等方面。 安装 安装SQLGlot库非常简单,可以使用pip命令进行安装: pip install sqlglot安装完成后…...

NULL—0—nullptr 三者关系
1.概述 NULL,0,nullptr值都是0,但是类型不同,但是由于C头文件中NULL定义宏混乱,可能是int 0,也可能是(void*)0; 所以在C11及以后的标准中引入新的空指针nullptr,nullptr就是(void*)0ÿ…...

Nginx 请求的 匹配规则 与 转发规则
博文目录 文章目录 URL 与 URI匹配规则案例说明 转发规则响应静态资源案例说明 转发动态代理案例说明案例说明 URL 与 URI 通常, 一个 URL 由以下部分组成 scheme://host:port/path?query#fragment scheme: 协议, 如 http, https, ftp 等host; 主机名或 IP 地址post: 端口…...

OWASP发布10大开源软件风险清单
3月20日,xz-utils 项目被爆植入后门震惊了整个开源社区,2021 年 Apache Log4j 漏洞事件依旧历历在目。倘若该后门未被及时发现,那么将很有可能成为影响最大的软件供应链漏洞之一。近几年爆发的一系列供应链漏洞和风险,使得“加强开…...

大学生前端学习第一天:了解前端
引言: 哈喽,各位大学生们,大家好呀,在本篇博客,我们将引入一个新的板块学习,那就是前端,关于前端,GPT是这样描述的:前端通常指的是Web开发中用户界面的部分,…...
公安机关人民警察证照片采集规范及自拍制作电子版指南
在当今社会,证件照的拍摄已成为我们生活中不可或缺的一部分。无论是办理身份证、驾驶证还是护照,一张规范的证件照都是必需的。而对于公安机关的人民警察来说,证件照片的采集更是有着严格的规范和要求。本文将为您详细介绍公安机关人民警察证…...

使用Python插入100万条数据到MySQL数据库并将数据逐步写出到多个Excel
Python插入100万条数据到MySQL数据库 步骤一:导入所需模块和库 首先,我们需要导入 MySQL 连接器模块和 Faker 模块。MySQL 连接器模块用于连接到 MySQL 数据库,而 Faker 模块用于生成虚假数据。 import mysql.connector # 导入 MySQL 连接…...

【备忘录】openssl记录
openssl genrsa -out ca.key 2048 openssl req -x509 -new -nodes -key ca.key -days 10000 -out ca.crt -subj “/CCN/STBeijing/LBeijing/Okubernetes/OUKubernetes-manual/CNkubernetes-ca” openssl genrsa -out etcd-ca.key 2048 openssl req -x509 -new -nodes -key etc…...
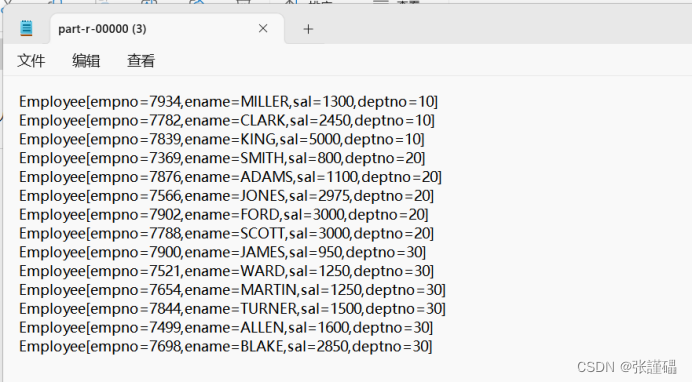
hadoop编程之工资序列化排序
数据集展示 7369SMITHCLERK79021980/12/17800207499ALLENSALESMAN76981981/2/201600300307521WARDSALESMAN76981981/2/221250500307566JONESMANAGER78391981/4/22975207654MARTINSALESMAN76981981/9/2812501400307698BLAKEMANAGER78391981/5/12850307782CLARKMANAGER78391981/…...

OpenXR手部跟踪接口与VIVE OpenXR扩展详细解析
随着虚拟现实技术的发展,手部跟踪已成为提高沉浸感和交互性的关键技术。OpenXR标准为开发者提供了一套手部跟踪的扩展接口,特别是针对VIVE设备的特定实现。以下是这些接口和类的详细解释: 1. VIVE.OpenXR.Hand VIVE.OpenXR.Hand 是HTC VIVE…...
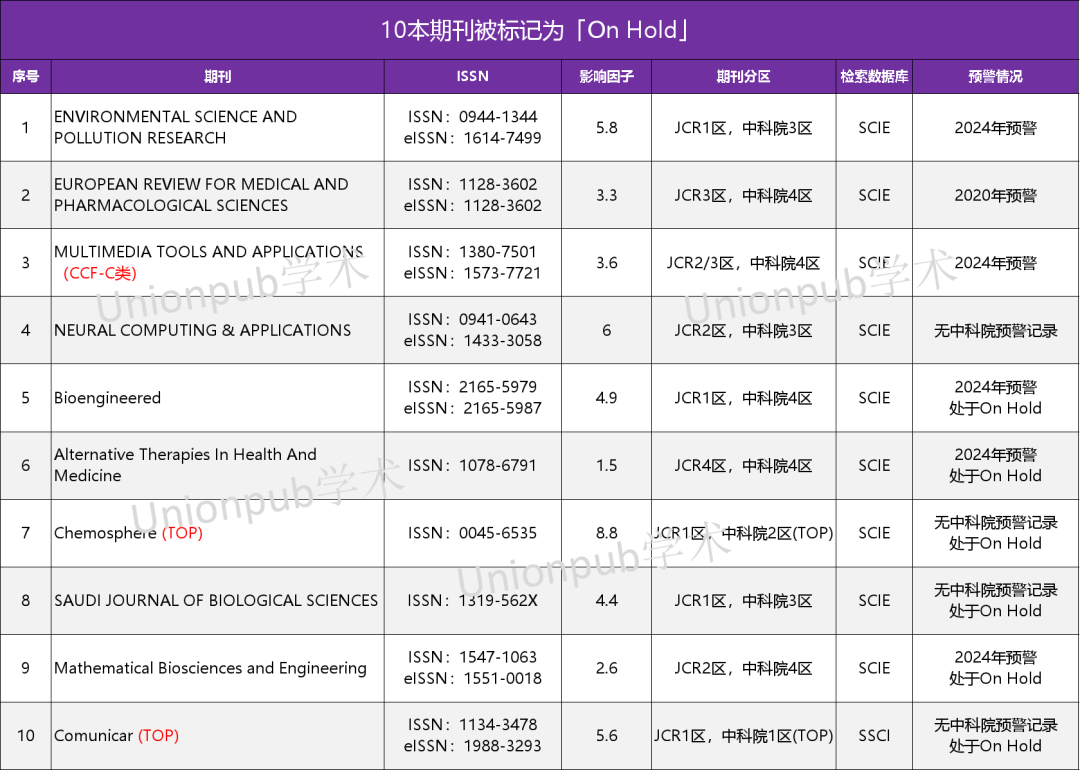
慎投!5本On Hold全被剔除!新增9本SCI/SSCI被除名!4月WOS更新
本周投稿推荐 SSCI • 2/4区经管类,2.5-3.0(录用率99%) SCIE(CCF推荐) • 计算机类,2.0-3.0(最快18天录用) SCIE(CCF-C类) • IEEE旗下,1/2…...
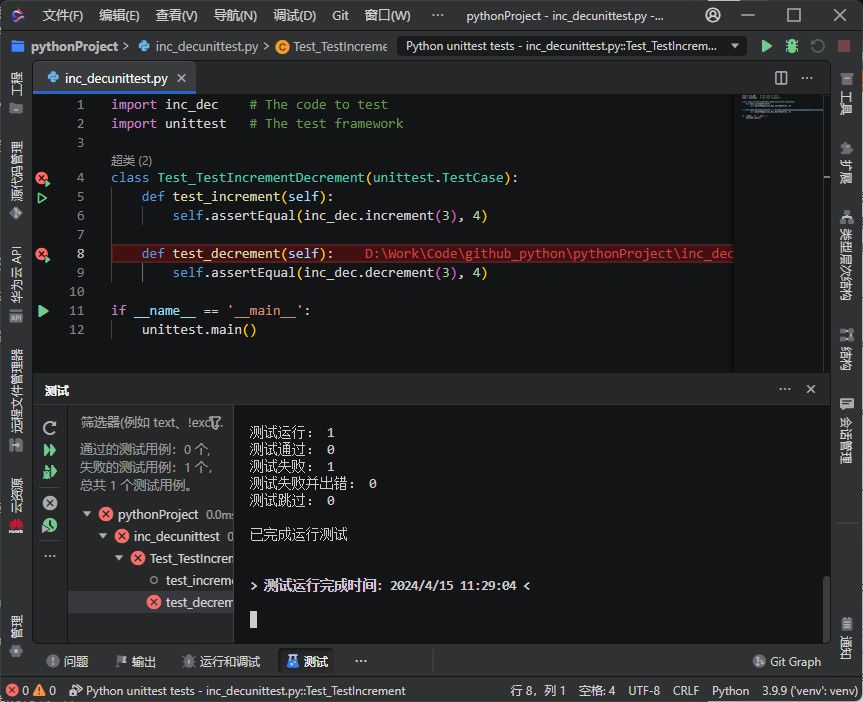
华为云CodeArts IDE For Python 快速使用指南
CodeArts IDE 带有 Python 扩展,为 Python 语言提供了广泛的支持。Python 扩展可以利用 CodeArts IDE 的代码补全、验证、调试和单元测试等特性,与多种 Python 解释器协同工作,轻松切换包括虚拟环境和 conda 环境的 Python 环境。本文简要概述…...

C# 截图并保存为图片
在winform开发中,有时会用到截图并保存为图片的时候,这里列了三种保存图片的可能情况。 将窗体截图保存成图片的方式是: Bitmap bit new Bitmap(this.Width, this.Height);//实例化一个和窗体一样大的bitmap Graphics g Graphics.FromImag…...

[html]一个动态js倒计时小组件
先看效果 代码 <style>.alert-sec-circle {stroke-dasharray: 735;transition: stroke-dashoffset 1s linear;} </style><div style"width: 110px; height: 110px; float: left;"><svg style"width:110px;height:110px;"><cir…...
Hive-Sql复杂面试题
参考链接:hive sql面试题及答案 - 知乎 有哪些好的题目都可以给我哦 我来汇总到一起 1、编写sql实现每个用户截止到每月为止的最大单月访问次数和累计到该月的总访问次数 数据: userid,month,visits A,2015-01,5 A,2015-01,15 B,2015-01,5 A,2015-01,…...
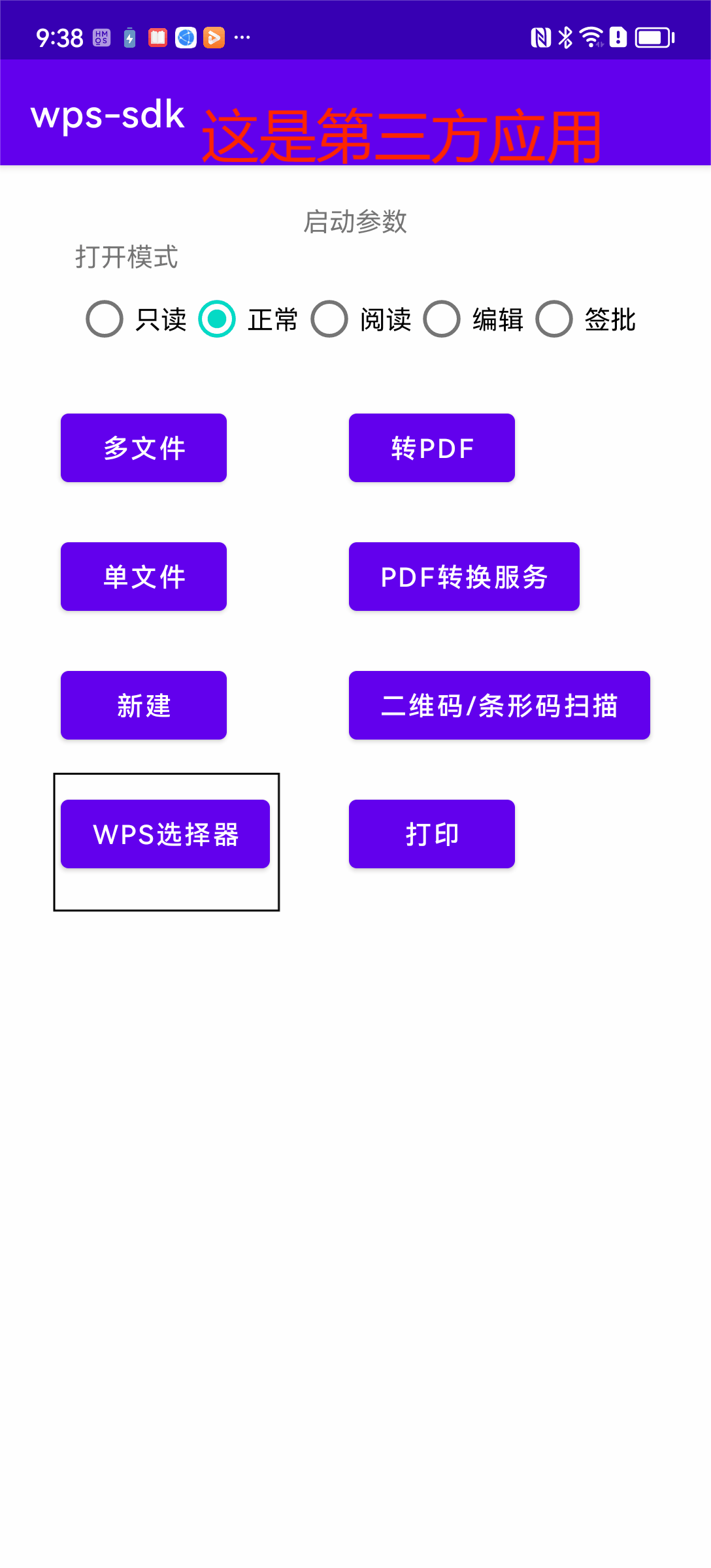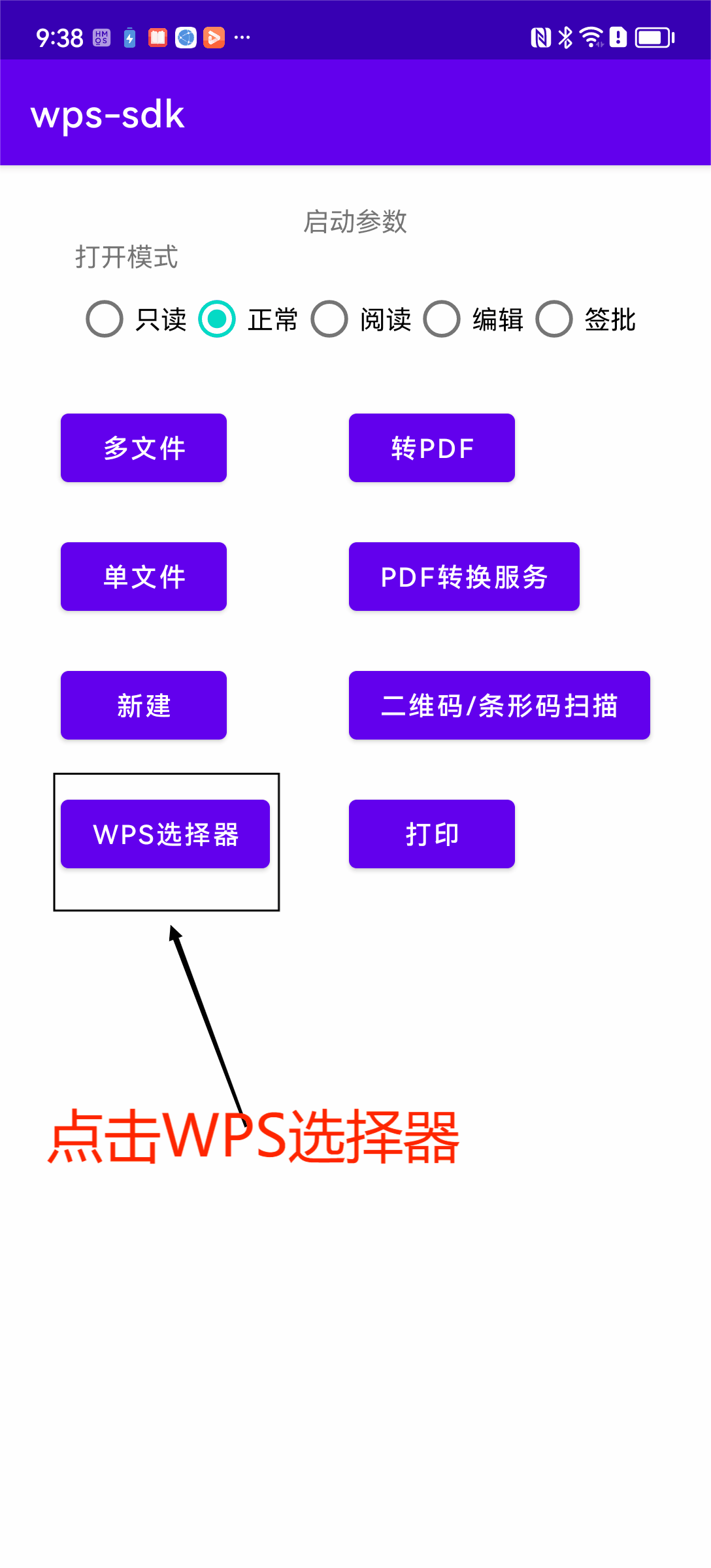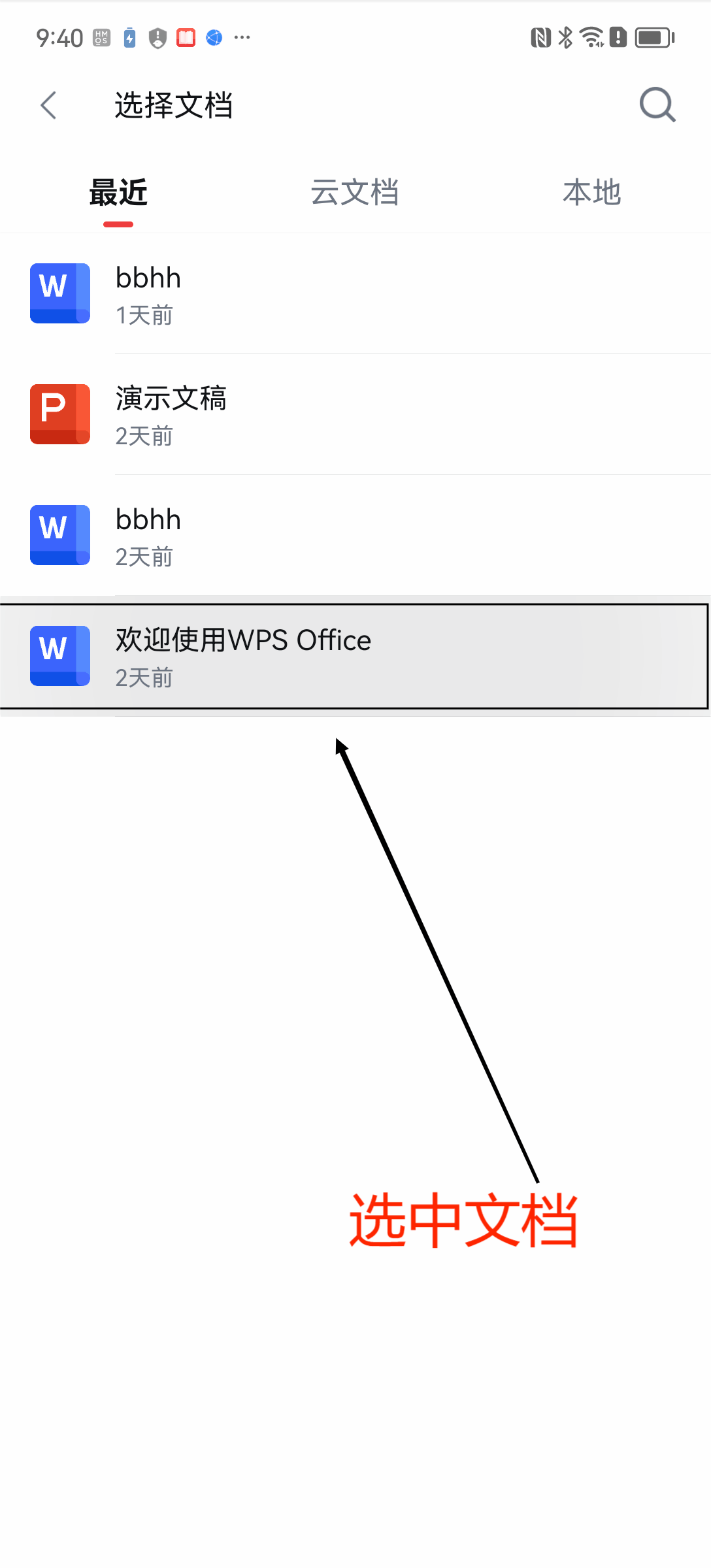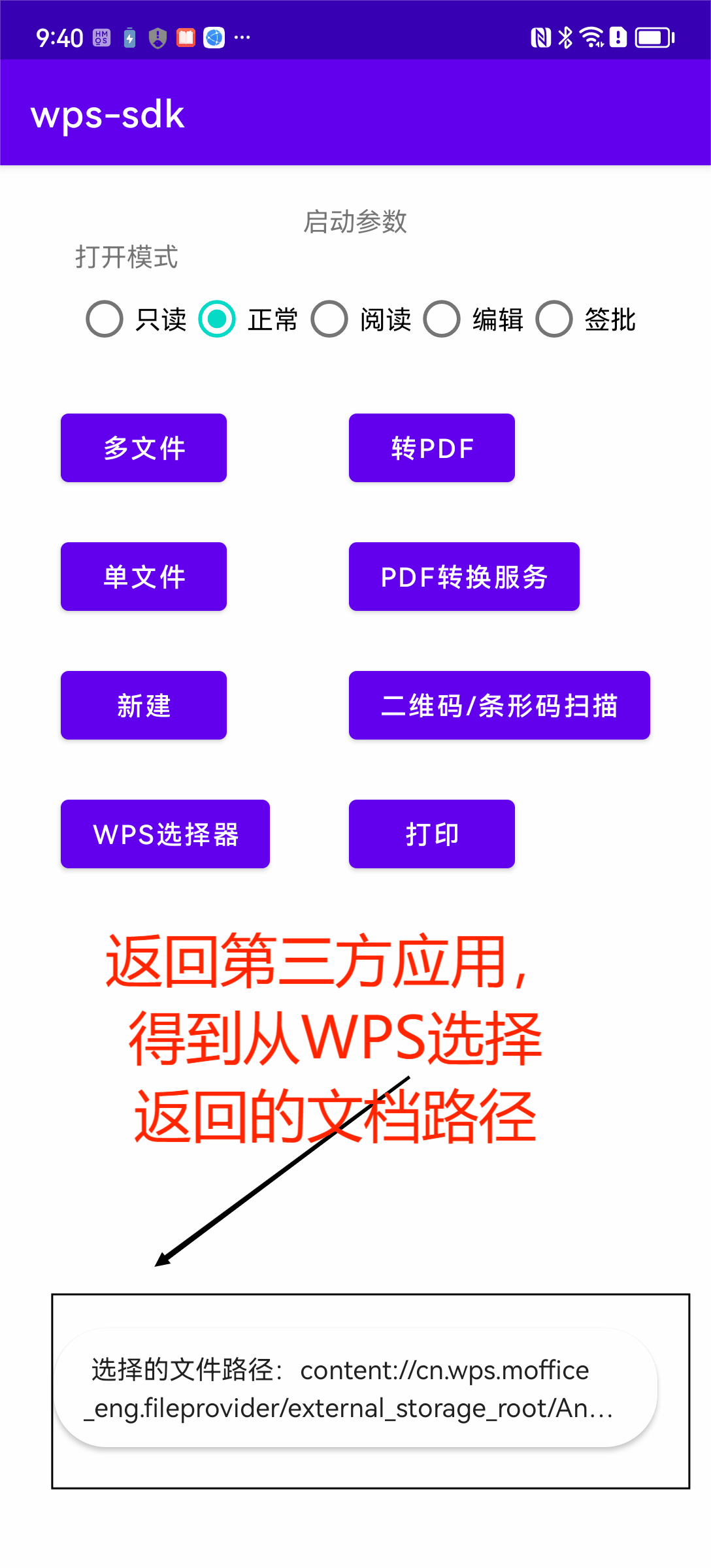
WPS二次开发系列:WPS SDk功能就概览
作者持续关注WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(QQ:250325397) 作者通过深度测试使用了WPS SDK提供的Demo࿰…...

华为OD-C卷-结队编程[200分]
题目描述 某部门计划通过结队编程来进行项目开发, 已知该部门有 N 名员工,每个员工有独一无二的职级,每三个员工形成一个小组进行结队编程, 结队分组规则如下: 从部门中选出序号分别为 i、j、k 的3名员工,他们的职级分别为 level[i],level[j],level[k], 结队小组满…...

连连看游戏页面网站源码,直接使用
可以上传自己喜欢的图片 游戏页面 通关页面 源码免费下载地址抄笔记 (chaobiji.cn)...

在 Kubernetes 1.24 中使用 Docker:配置与应用指南
在 Kubernetes 1.24 中使用 Docker:配置与应用指南 引言 随着 Kubernetes 社区对容器运行时接口(CRI)的标准化推进,Docker 原生支持在 Kubernetes 1.24 版本中被弃用。然而,许多开发者和组织仍希望继续使用 Docker。…...

Canvas使用详细教学:从基础绘图到进阶动画再到实战(海报生成、Flappy Bird 小游戏等),掌握绘图与动画的秘诀
一、Canvas基础 1. Canvas简介 Canvas是HTML5引入的一种基于矢量图形的绘图技术,它是一个嵌入HTML文档中的矩形区域,允许开发者使用JavaScript直接操作其内容进行图形绘制。Canvas元素不包含任何内在的绘图能力,而是提供了一个空白的画布&a…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
