【应用】SpringBoot-自动配置原理
前言
本文简要介绍SpringBoot的自动配置原理。
本文讲述的SpringBoot版本为:3.1.2。
前置知识
在看原理介绍之前,需要知道@Import注解的作用:
- 可以导入@Configuration注解的配置类、声明@Bean注解的bean方法;
- 可以导入ImportSelector的实现类;【自动配置原理用到注解的这个作用】
- 可以导入ImportBeanDefinitionRegistrar的实现类。
原理介绍
从启动类入手
一个常规的SpringBoot项目的启动类内容如下:
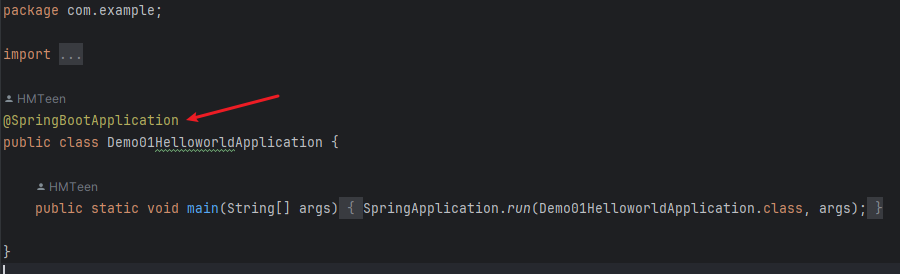
从启动类上的@SpringBootApplication入手:
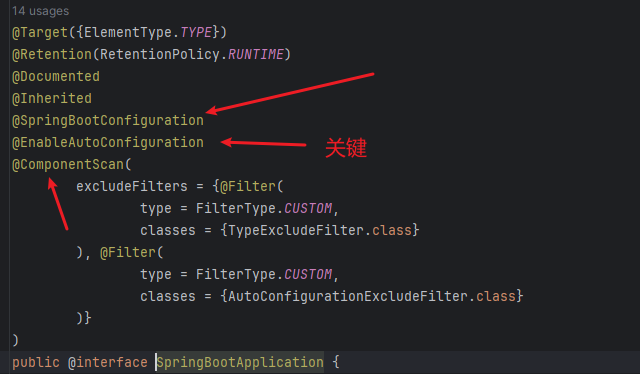
三个注解箭头指示的注解,各有各的作用:
@SpringBootConfiguration:组合了@Configuration注解,表示这是一个配置类@EnableAutoConfiguration:允许自动配置@ComponentScan:Spring的组件扫描,默认扫描main方法所在类所在的包及其子包
其中第二个注解@EnableAutoConfiguration是实现自动配置的关键。
从@EnableAutoConfiguration注解入手:
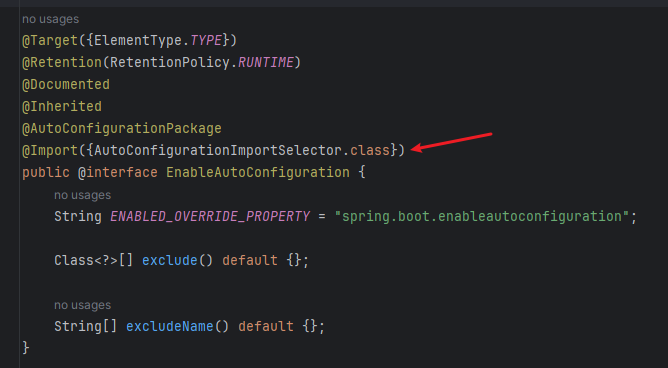
可以看到该注解中有一个@Import注解,先说结论:在AutoConfigurationImportSelector类中加载了哪些需要自动配置的Bean,并完成加载,注入到IOC容器中。
到AutoConfigurationImportSelector类
从AutoConfigurationImportSelector类入手:
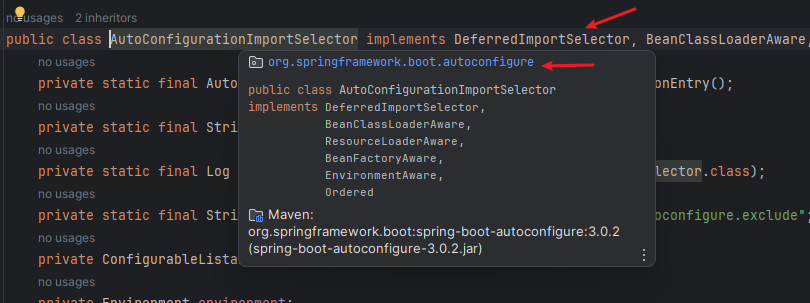
可以看出:AutoConfigurationImportSelector类是org.springframework.boot.autoconfigure包下的一个类,实现了DeferredImportSelector等接口
org.springframework.boot.autoconfigure:望名生意,自动配置,就是在该包里面,规定了哪些Bean需要配置。DeferredImportSelector:该接口是实现自动配置的关键,里面的selectImports方法规定了哪些Bean需要自动配置。
往下滑,看AutoConfigurationImportSelector类的selectImports方法:
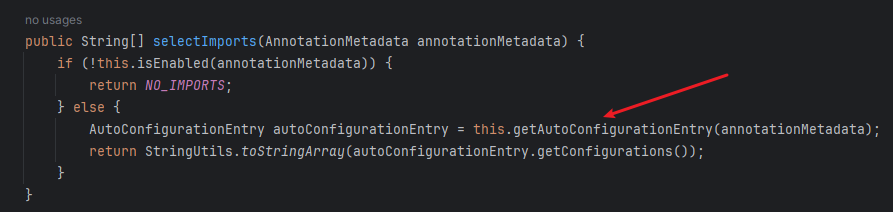
红框所示代码:返回了需要自动配置的Bean列表。
从this.getAutoConfigurationEntry方法入手:
protected AutoConfigurationEntry getAutoConfigurationEntry(AnnotationMetadata annotationMetadata) {if (!this.isEnabled(annotationMetadata)) {return EMPTY_ENTRY;} else {AnnotationAttributes attributes = this.getAttributes(annotationMetadata);// 获取该类所在包下的META-INF/spring/目录中以.imports为后缀结尾的文件里面的内容,作为候选配置列表List<String> configurations = this.getCandidateConfigurations(annotationMetadata, attributes);// 去除重复的配置configurations = this.removeDuplicates(configurations);// 排除部分元注解信息中需要排除的配置Set<String> exclusions = this.getExclusions(annotationMetadata, attributes);this.checkExcludedClasses(configurations, exclusions);configurations.removeAll(exclusions);// 过滤掉一些暂时不生效的配置:加了如下注解的bean:@OnxxxConditionconfigurations = this.getConfigurationClassFilter().filter(configurations);this.fireAutoConfigurationImportEvents(configurations, exclusions);return new AutoConfigurationEntry(configurations, exclusions);}
}
该方法中代码的逻辑如上。就剩一个this.getCandidateConfigurations方法需要再探究,里面规定了从哪个地方寻找需要配置的bean列表。
从this.getCandidateConfigurations方法入手:

再进入箭头所指向的load方法:
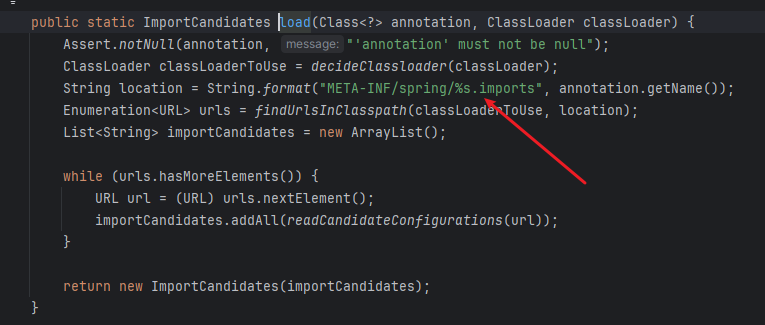
可以看到:该方法往包下的META-INF/spring/目录中寻找后缀名为.imports的文件。
到org.springframework.boot.autoconfigure包中看看
从idea左侧的依赖列表里面查看:
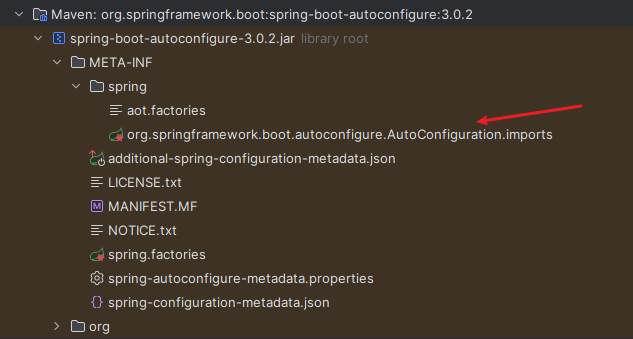
点开文件里面任意一个类:
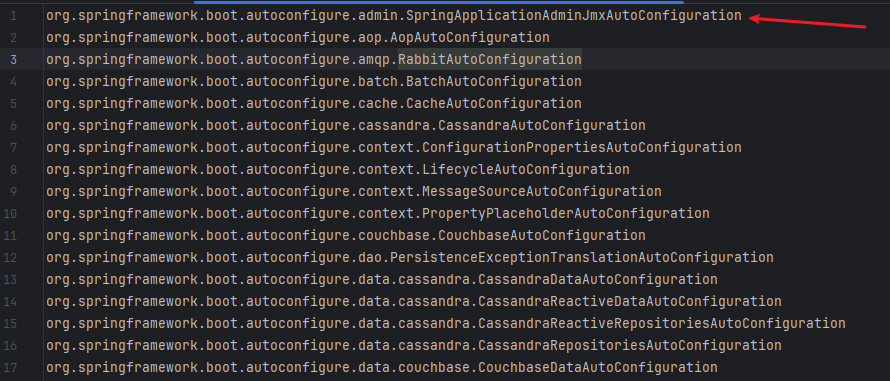
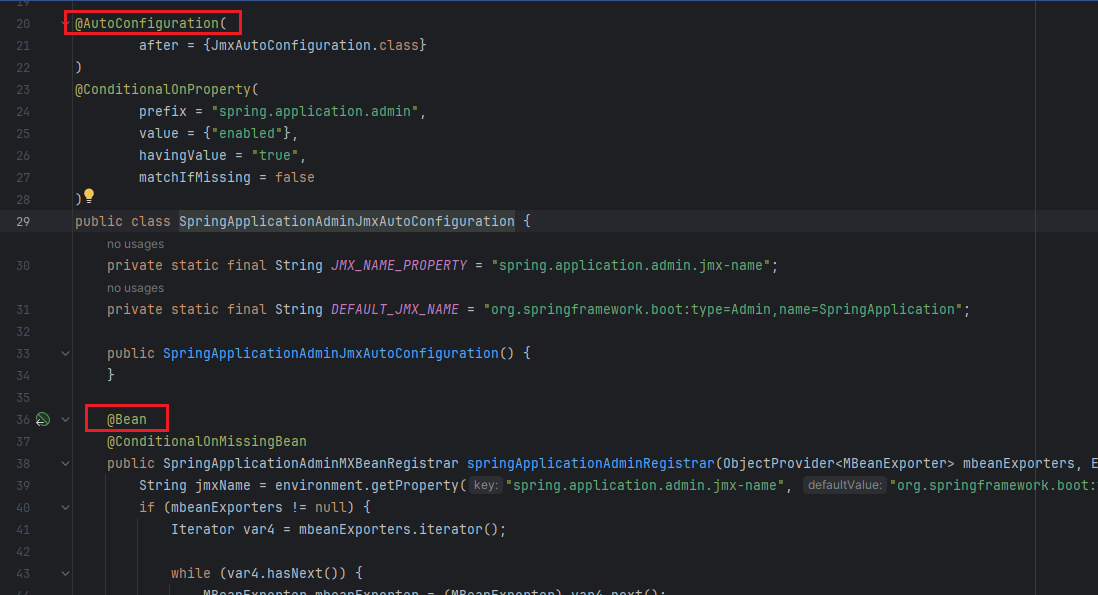
都是一个自动配置类,定义有相应的Bean方法。
至此,SpringBoot的自动配置原理就明白了。
原理总结
- 启动类中有一个@SpringBootApplication注解,包含了@EnableAutoConfiguration代表开启自动装配
- @EnableAutoConfiguration注解里面组合了一个
@Import注解,这个注解是实现自动配置的关键。 @Import注解最终的作用可以总结如下:到spring-boot-autoconfigure包下的META-INF/spring目录中寻找.imports结尾的文件,这里面列举了所有需要自动配置的类,程序会读取这些类并加载(但这些类不会全部加载,因为有的类上面有条件注解,需要满足特定条件时才会生效)- spring-boot-autoconfigure包下的
AutoConfigurationImportSelector类实现了ImportSelector,并重写了selectImports方法 - 在
selectImports方法中,定义类自动配置类的加载位置。还有一些配置类的去重操作、排除操作等。
- spring-boot-autoconfigure包下的
相关文章:

【应用】SpringBoot-自动配置原理
前言 本文简要介绍SpringBoot的自动配置原理。 本文讲述的SpringBoot版本为:3.1.2。 前置知识 在看原理介绍之前,需要知道Import注解的作用: 可以导入Configuration注解的配置类、声明Bean注解的bean方法;可以导入ImportSele…...

中文编程入门(Lua5.4.6中文版)第十二章 Lua 协程 参考《愿神》游戏
在《愿神》的提瓦特大陆上,每一位冒险者都拥有自己的独特力量——“神之眼”,他们借助元素之力探索广袤的世界,解决谜题,战胜敌人。而在提瓦特的科技树中,存在着一项名为“协同程序”的高级秘术,它使冒险者…...

C++笔记之注册回调函数常见的5种情况对比
C++笔记之注册回调函数常见的5种情况对比 —— 2024-04-10 code review! 文章目录 C++笔记之注册回调函数常见的5种情况对比1.五种情况2.示例2.1. `RegisterCallback` 和 `Callback` 都是普通函数2.2. `RegisterCallback` 是成员函数,`Callback` 是普通函数2.3. `RegisterC…...

人工智能揭示矩阵乘法的新可能性
人工智能揭示矩阵乘法的新可能性 数学家酷爱漂亮的谜题。当你尝试找到最有效的方法时,即使像乘法矩阵(二维数字表)这样抽象的东西也会感觉像玩一场游戏。这有点像尝试用尽可能少的步骤解开魔方——具有挑战性,但也很诱人。除了魔方…...

实在智能携手长江新零售俱乐部:探秘实在Agent数字员工,开启零售品牌增长新篇章
近日,实在智能携手长江新零售俱乐部成功举办了“AIGC:数字员工助力零售品牌新增长”主题活动,成功吸引了二十余家企业中高层管理精英的踊跃参与。在此次活动中,与会者围绕零售业数字化转型的当前态势、面临的挑战及其重要性进行了…...

计算机科学与导论 第十七 十八章 计算理论,人工智能
文章预览: 计算理论17.1 引言17.2 简单语言17.3 图灵机邱奇 -图灵 论题 人工智能引言18.1.1 什么是人工智能18.1.2 智能体18.1.3 编程语言 18.2 知识的表示18.2.1 语义网18.2.2 框架18.2.3 谓词逻辑18.2.4 基于规则的系统 18.2 专家系统18.3 语言理解18.4 搜索18.5 …...
linux 设置定时任务---学习
1、设置定时任务 crontab -e 设置格式参考:【Linux】Linux crontab 命令定时任务设置_crontab 设置每天10:30执行-CSDN博客 测试过程: */1 * * * * /root/cronjob.sh 脚本内容: echo "hell0 cronjob" >> /root/test/hello.txt 实现…...

钡铼IOy系列模块深挖工业场景需求提供丰富多样的I/O解决方案
钡铼IOy系列模块以其灵活性和多样性,在工业场景中提供了丰富多样的I/O解决方案,满足了不同行业、不同应用场景的需求。以下是一些常见的工业场景需求及钡铼IOy系列模块提供的解决方案: 1. 工厂自动化 需求:工厂自动化需要对生产线…...

【刷题笔记】第三天
两道简单题 文章目录 [2923. 找到冠军 I](https://leetcode.cn/problems/find-champion-i/description/)[3095. 或值至少 K 的最短子数组 I](https://leetcode.cn/problems/shortest-subarray-with-or-at-least-k-i/description/) 2923. 找到冠军 I 方法1: 如果 i …...
开源模型应用落地-LangChain试炼-CPU调用QWen1.5(一)
一、前言 尽管现在的大语言模型已经非常强大,可以解决许多问题,但在处理复杂情况时,仍然需要进行多个步骤或整合不同的流程才能达到最终的目标。然而,现在可以利用langchain来使得模型的应用变得更加直接和简单。 通过langchain框…...
STM32-模数转化器
ADC(Analog-to-Digital Converter) 指模数转换器。是指将连续变化的模拟信号转换 为离散的数字信号的器件。 ADC相关参数说明: 分辨率: 分辨率以二进制(或十进制)数的位数来表示,一般有 8 位、10 位、12 位、16 位…...

算法刷题记录2
4.图 4.1.被围绕的区域 思路:图中只有与边界上联通的O才不算是被X包围。因此本题就是从边界上的O开始递归,找与边界O联通的O,并标记为#(代表已遍历),最后图中剩下的O就是:被X包围的O。图中所有…...

中国代工巨头旗下芯片公司遭网络攻击,千兆字节数据被泄露
近日,中国智能手机代工巨头闻泰科技旗下荷兰芯片制造商Nexperia发布声明,称其遭遇网络攻击,有未经授权的第三方访问了公司的 IT 服务器,目前已向相关部门报告了此次事件,并与网络安全专家合作开启调查。而据相关消息&a…...
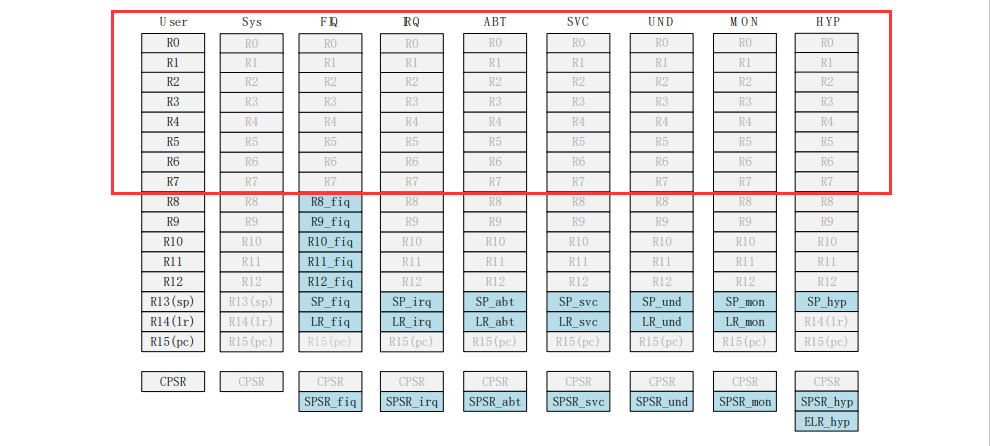
【ARM 裸机】汇编 led 驱动之基本语法
我们要编写的是 ARM 汇编,编译使用的是 gcc 交叉编译器,所以要符合 GNU 语法。 1、汇编指令 汇编由一条条指令构成,ARM 不能直接访问存储器,比如 RAM 中的数据,I.MX6UL 中的寄存器就是 RAM 类型的,我们用…...
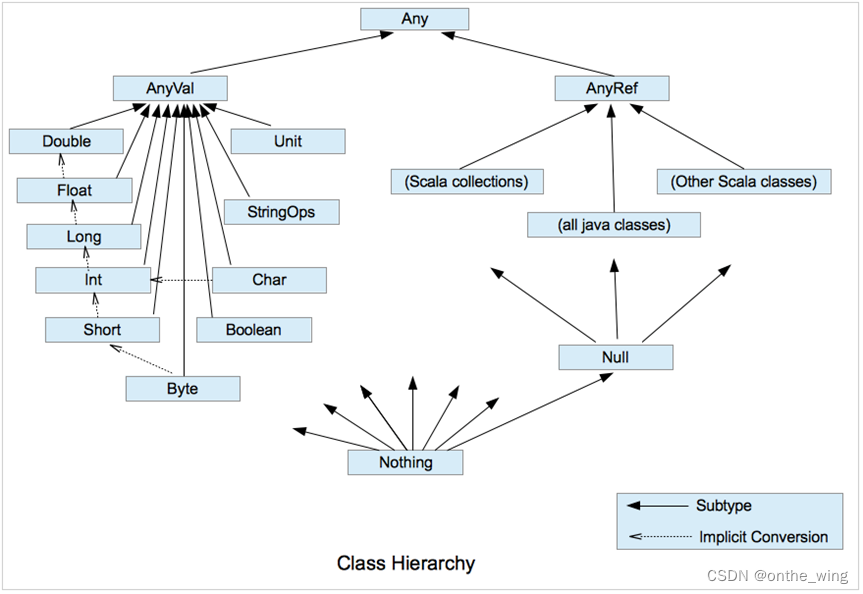
scala---基础核心知识(变量定义,数据类型,流程控制,方法定义,函数定义)
一、什么是scala Scala 是一种多范式的编程语言,其设计初衷是要集成面向对象编程和函数式编程的各种特性。Scala运行于Java平台(Java虚拟机),并兼容现有的Java程序。 二、为什么要学习scala 1、优雅 2、速度快 3、能融合到hado…...
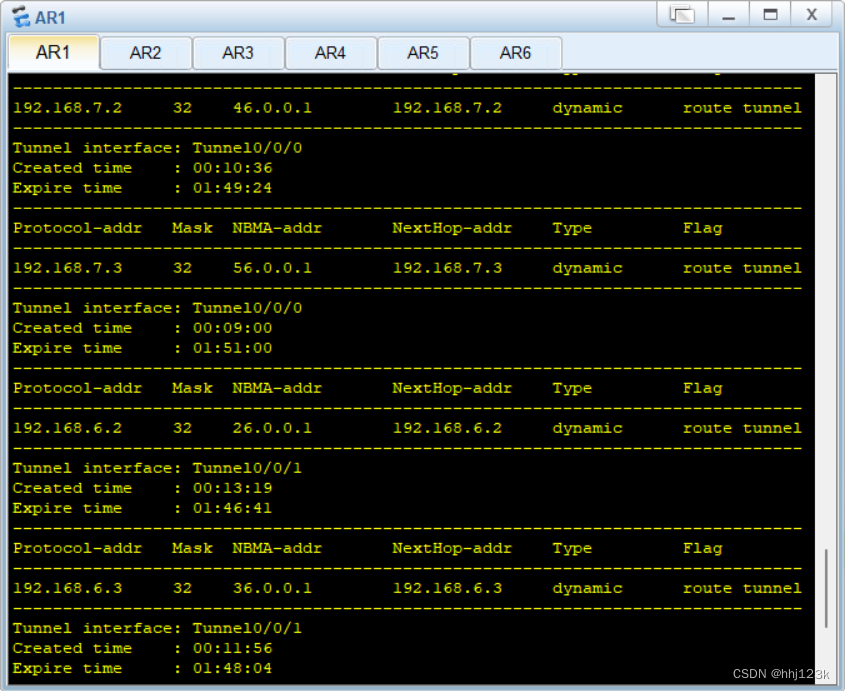
OSPF星型拓扑和MGRE全连
一,拓扑 二,要求 1,R6为ISP只能配置IP地址,R1-R5的环回为私有网段 2,R1/4/5为全连的MGRE结构,R1/2/3为星型的拓扑结构, 3,R1为中心站点所有私有网段可以互相通讯,私有网段…...
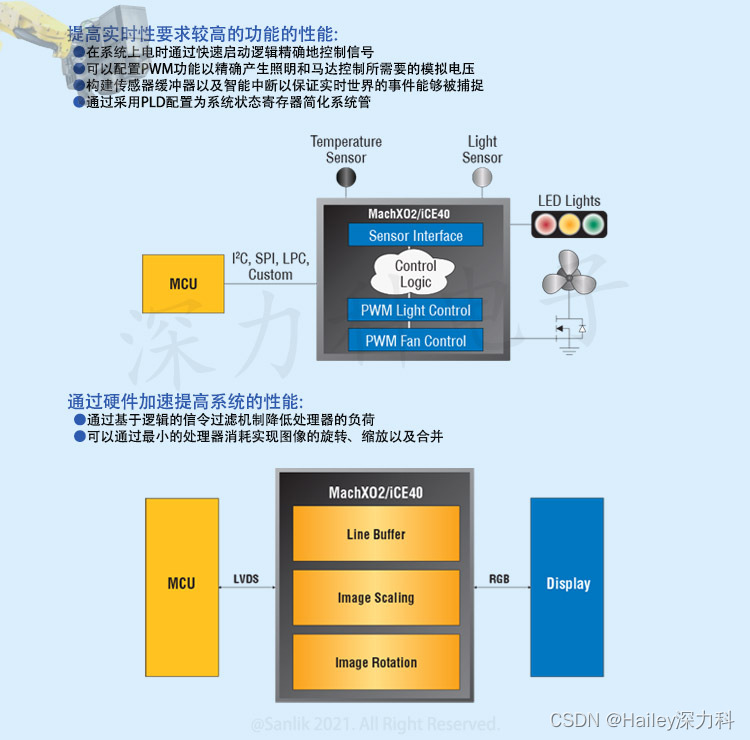
智能时代中的工业应用中前所未有的灵活桥接和I/O扩展功能解决方案MachXO2系列LCMXO2-1200HC-4TG100I FPGA可编程逻辑IC
lattice莱迪斯 MachXO2系列LCMXO2-1200HC-4TG100I超低密度FPGA现场可编程门阵列,适用于低成本的复杂系统控制和视频接口设计开发,满足了通信、计算、工业、消费电子和医疗市场所需的系统控制和接口应用。 瞬时启动,迅速实现控制——启动时间…...
php:实现压缩文件上传、解压、文件更名、压缩包删除功能
效果图 1.上传文件 2.压缩包文件 3.itemno1文件 或 4.上传到系统路径\ItemNo 5.更名后的itemno1文件(命名:当天日期六位随机数) 代码 <form action"<?php echo htmlspecialchars($_SERVER[PHP_SELF], ENT_QUOTES, UTF-8); ?>" methodpost en…...
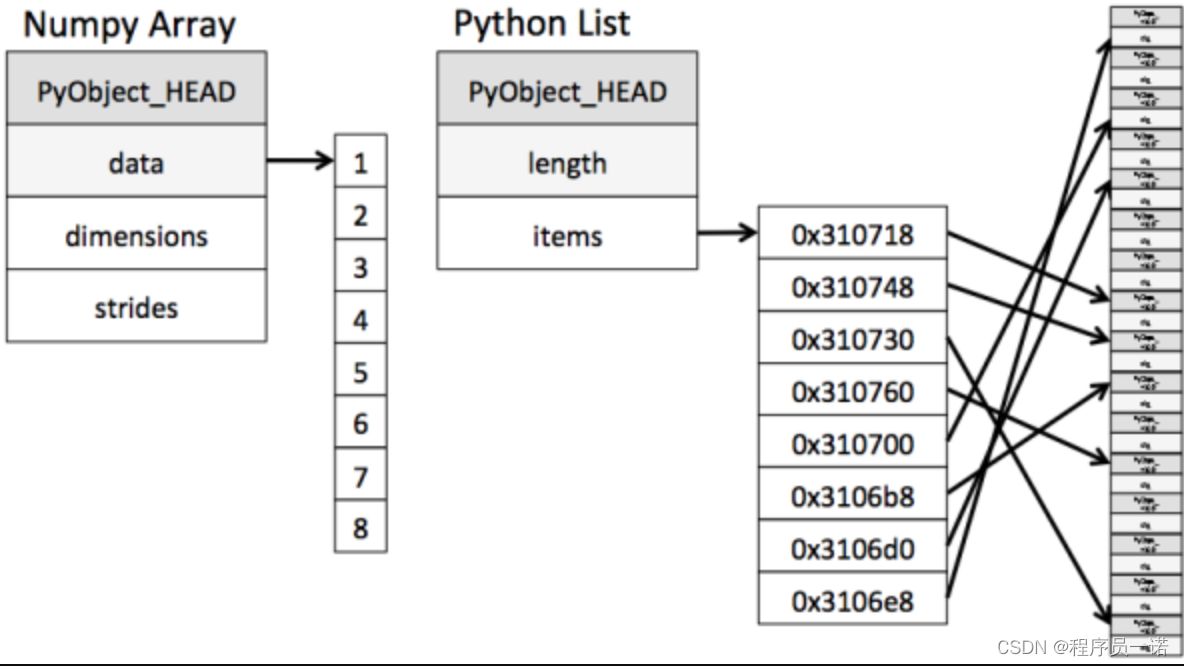
【机器学习】科学库使用第5篇:Matplotlib,学习目标【附代码文档】
机器学习(科学计算库)完整教程(附代码资料)主要内容讲述:机器学习(常用科学计算库的使用)基础定位、目标,机器学习概述定位,目标,学习目标,学习目标,1 人工智能应用场景,2 人工智能小…...
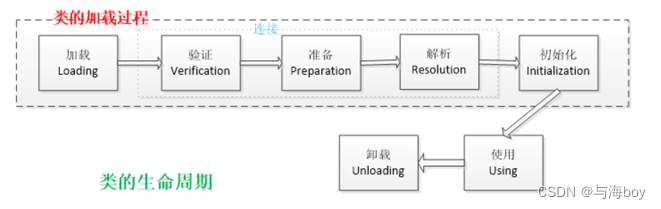
Java面试八股文(JVM篇)(❤❤)
Java面试八股文_JVM篇 1、知识点汇总2、知识点详解:3、说说类加载与卸载11、说说Java对象创建过程12、知道类的生命周期吗?14、如何判断对象可以被回收?17、调优命令有哪些?18、常见调优工具有哪些20、你知道哪些JVM性能调优参数&…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
