数据结构——二叉树链式结构的实现(上)
二叉树概念
再看二叉树基本操作前,再回顾下二叉树的概念,
二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的。

从概念中可以看出,二叉树定义是递归式的
二叉树构成:根 左子树 右子树构成的。
前序遍历是 :根 左子树 右子树
中序遍历是 :左子树 根 右子树
后序遍历是:左子树 右子树 根
根据上面的插图 前序遍历应该是: 1 2 3 N N N 4 5 N N 6 N N
那么你能试着说出中序和后序吗?
中序和后序如下图所示,你看你写对了吗?
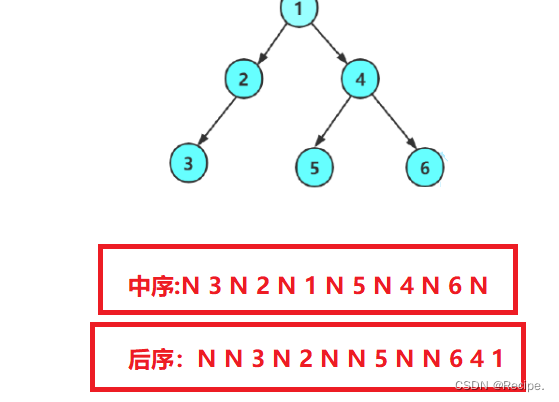

我们学习普通链式二叉树的增删查改是没有意义的,因为我们现在学习普通链式二叉树是为了以后的搜索二叉树和AVL 红黑树打基础的,还有就是很多二叉树的题,都是出在普通链式二叉树结构。
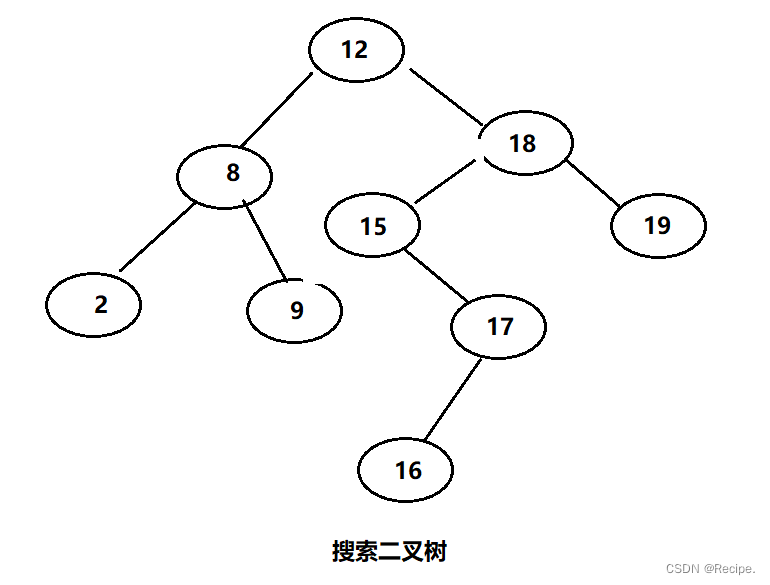
这是一个普通的搜索二叉树,二叉树的左子树比根小,右子树比根大。
如果搜索二叉树走中序遍历,就是个有序二叉树。
二叉树的构建
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。(注意:下述代码并不是创建二叉树的方式 )
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct BinaryTree
{struct BinaryTree* _left;struct BinaryTree* _right;int val;
}BTNode;BTNode* buynode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}
int main()
{BTNode* newnode1 = buynode(1);BTNode* newnode2 = buynode(2);BTNode* newnode3 = buynode(3);BTNode* newnode4 = buynode(4);BTNode* newnode5 = buynode(5);BTNode* newnode6 = buynode(6);newnode1->_left = newnode2;newnode2->_left = newnode3;newnode1->_right = newnode4;newnode4->_left = newnode5;newnode4->_right = newnode6;return 0;
}
二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}printf("%d ", root->val);PreOrder(root->_left);PreOrder(root->_right);
}是不是觉得很简单?我们先运行下结果
![]()

跟我们之前预测的一模一样,为了更好的了解前序遍历,我画一下递归图。
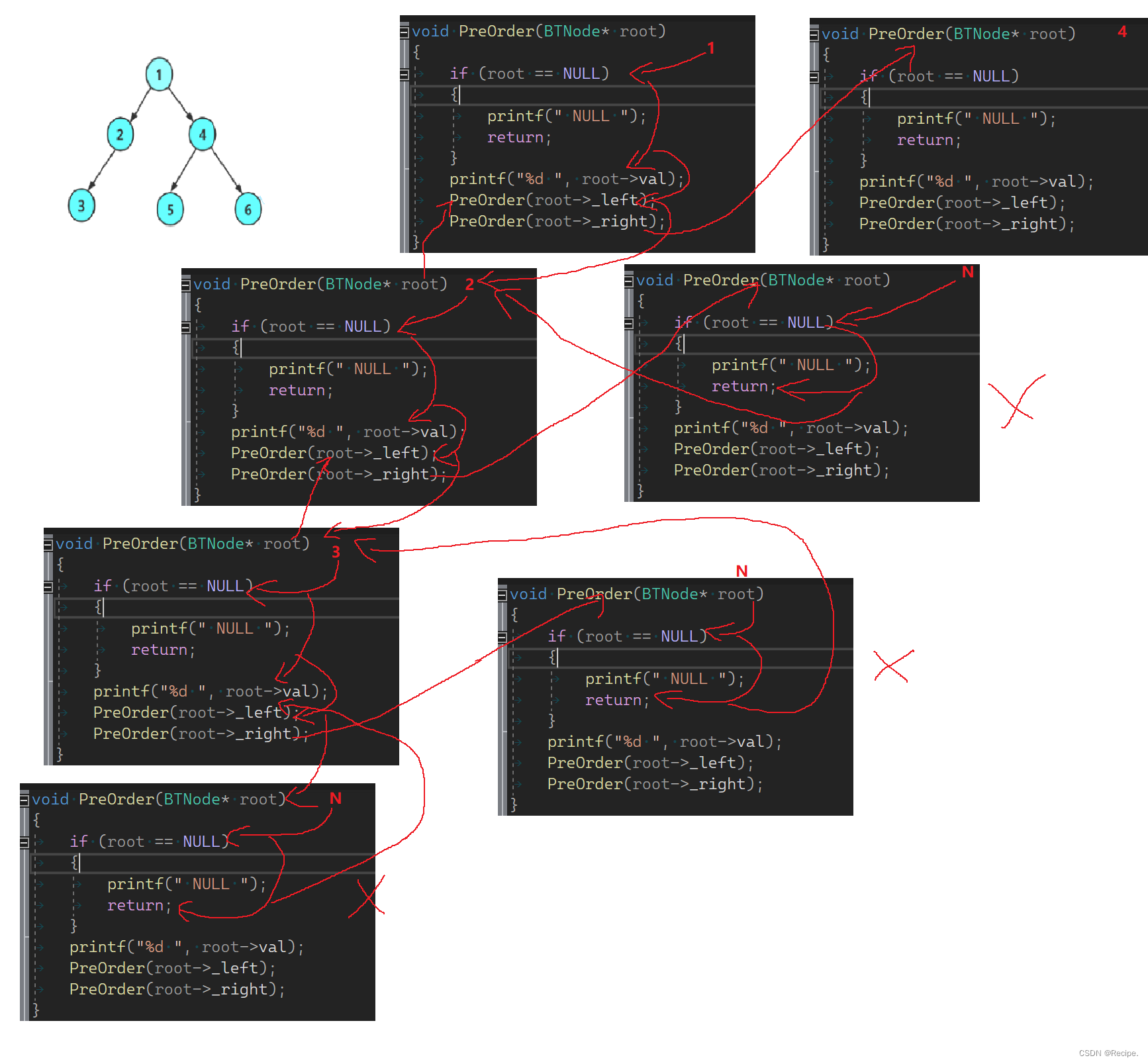
中序遍历
就是把代码换个顺序就变成了中序遍历,为了深刻理解递归过程,建议像上面一样,自己画个递归过程理解。
void InOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}InOrder(root->_left);printf("%d ", root->val);InOrder(root->_right);
}运行结果
![]()
后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%d ", root->val);
}运行结果
![]()
前序 中序 后序遍历结果

求节点个数以及高度等



二叉树的节点个数
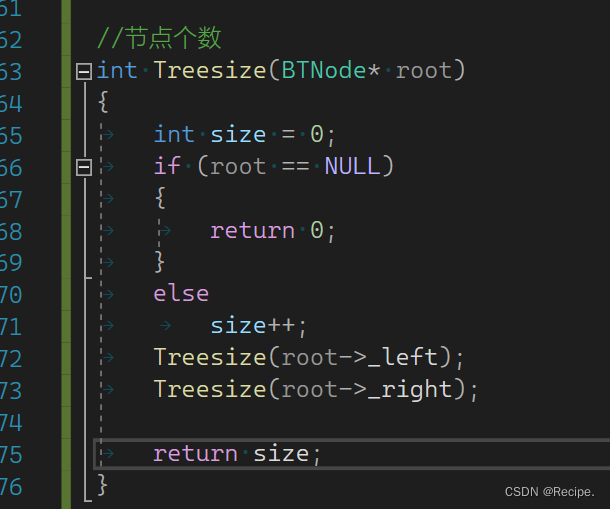
很多人可能都是想这么求节点个数的,但其实是错误的方法,因为size是局部变量 出了作用域就销毁了 根本求不出正确节点个数。
那么我们加上static 让它变成静态变量呢?
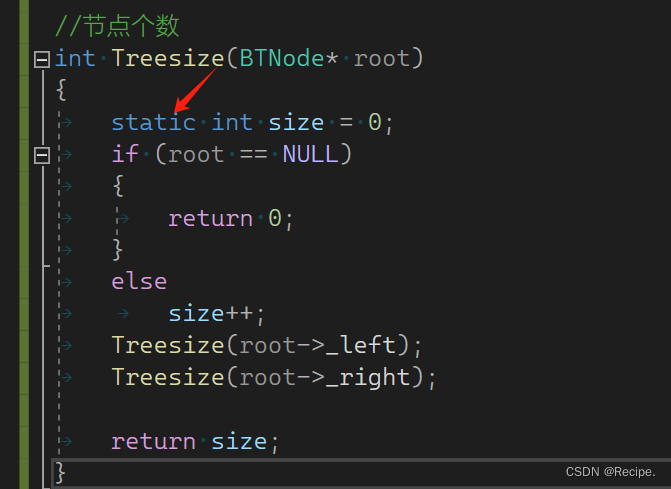
![]()
可以求出正确答案,因为静态变量在静态区,全局变量也在静态区,相当于一个全局变量,出了作用域并不会被销毁,而且只会走一次初始化,因此答案是正确的。
但有一个问题,如果我要再次调用这个函数求节点个数呢?

![]()
答案就会是错误的,因为静态变量只会走一次初始化。
解决办法也有,就是在前面把size设为全局变量 再次调用时归为0即可 答案还是6,但这种方法太low了。
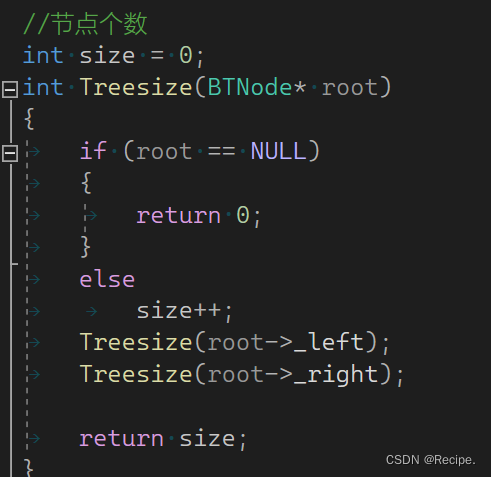
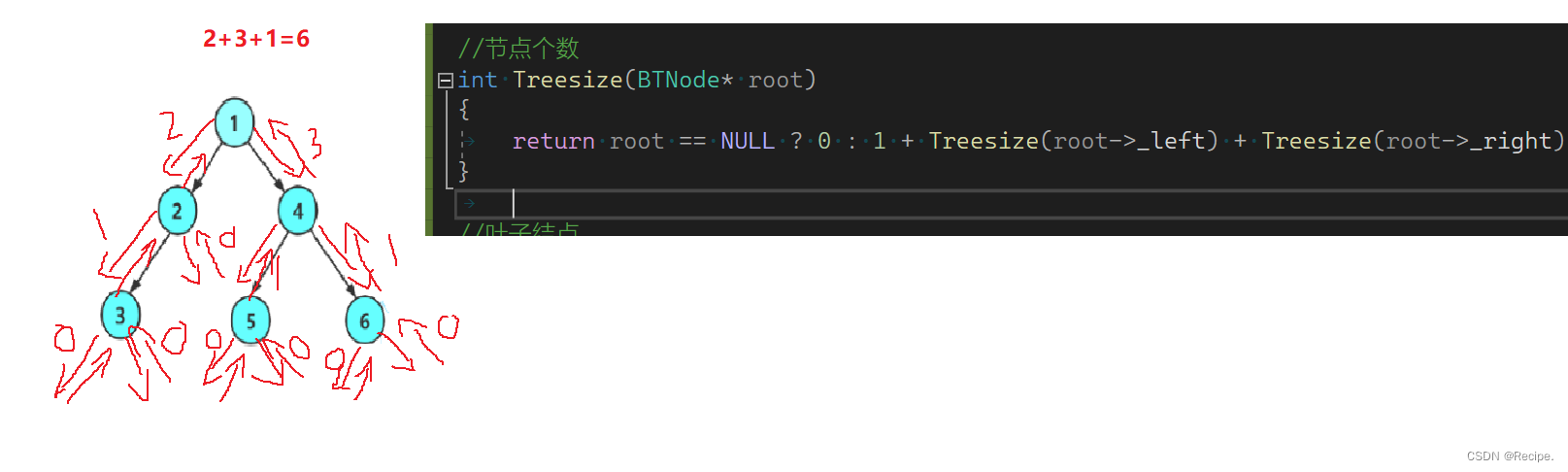
正确的求节点个数代码
//节点个数
int Treesize(BTNode* root)
{return root == NULL ? 0 : 1 + Treesize(root->_left) + Treesize(root->_right);
}![]()
思路:比如学校里面要统计在校人数,校长不可能一个个问每个人+1+1+1......,而是布置任务,给辅导员或者班主任,班主任或者辅导员会布置给班长去统计各班学生个数,班长汇报给辅导员或班主任,班主任或者辅导员汇报给校长,校长最后在汇报结果加上自己,就是学校在校总人数。
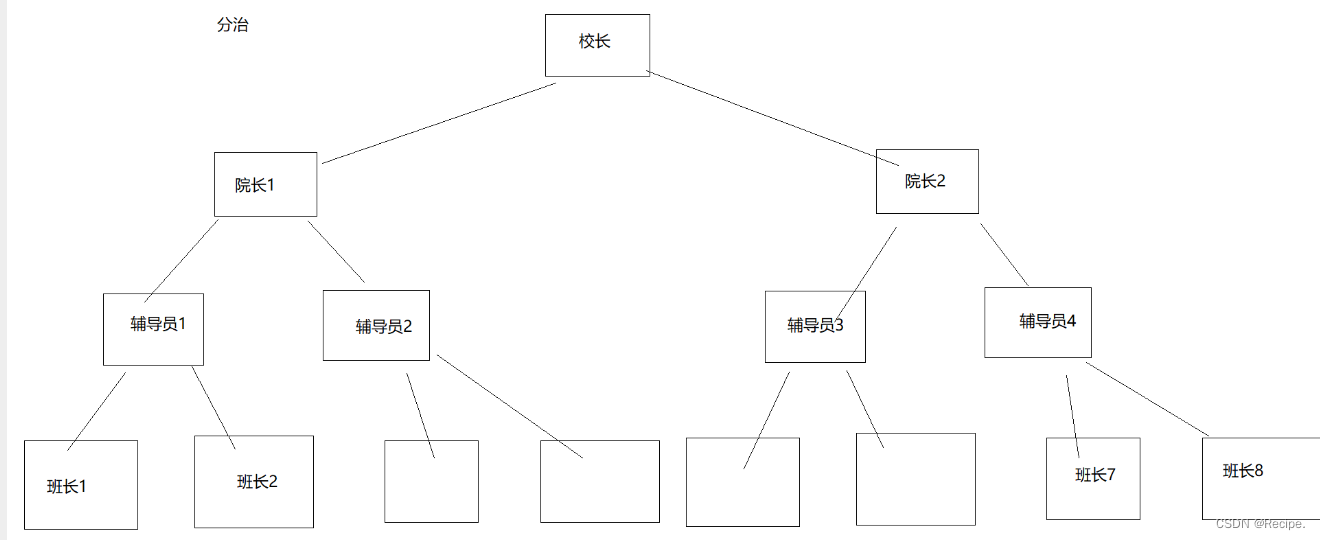
二叉树的叶子节点个数
叶子节点就是度为0的节点。
首先要判断根为不为空
再判断根节点的左右结点存不存在即可。
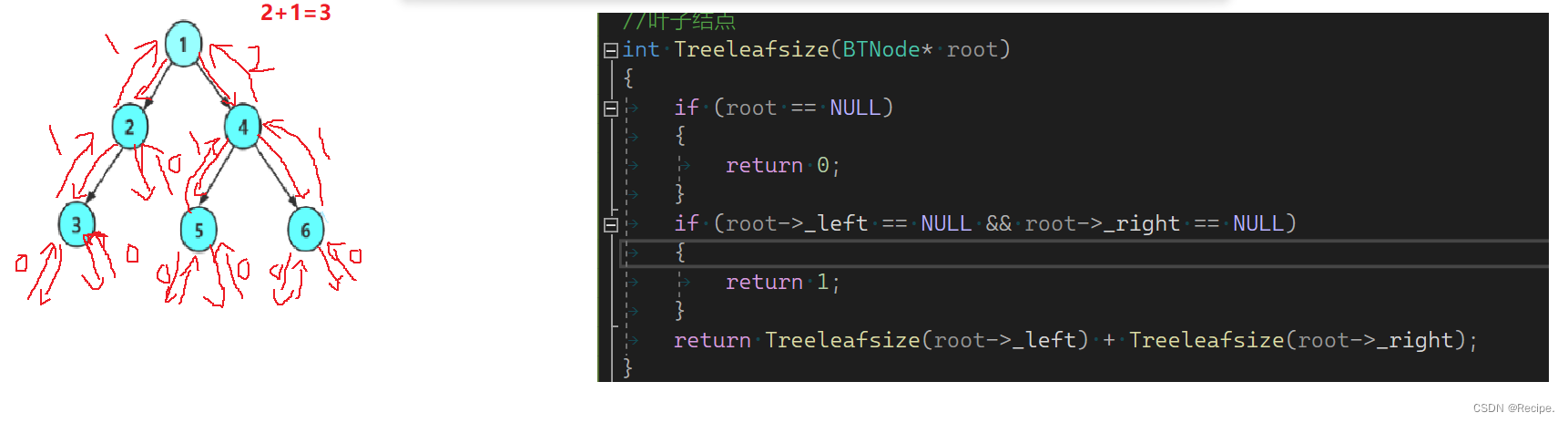
//叶子结点
int Treeleafsize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return Treeleafsize(root->_left) + Treeleafsize(root->_right);
}
![]()
二叉树第k层的节点个数
//第K层结点个数
int TreeKlevelsize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKlevelsize(root->_left, k - 1) + TreeKlevelsize(root->_right, k-1);
}![]()
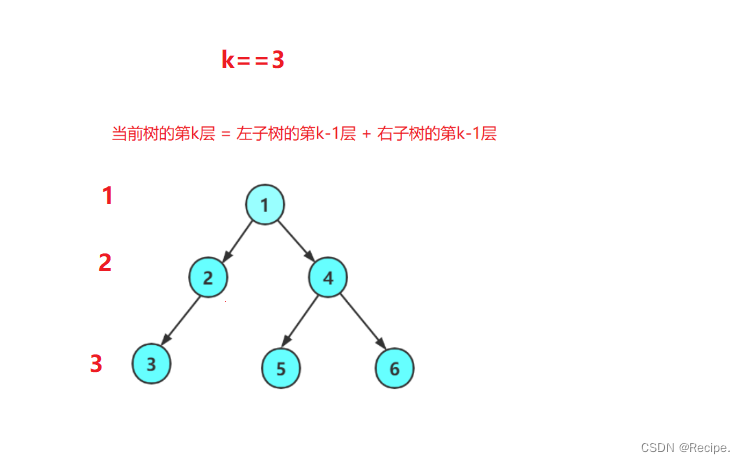
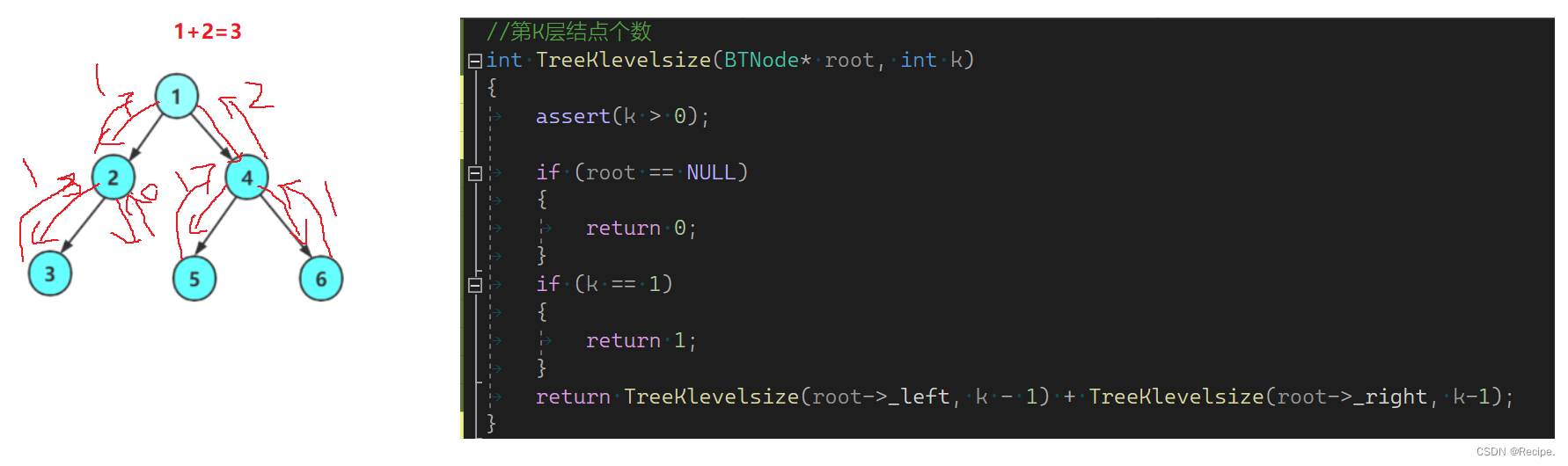
完整代码
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
typedef struct BinaryTree
{struct BinaryTree* _left;struct BinaryTree* _right;int val;
}BTNode;BTNode* buynode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}void PreOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}printf("%d ", root->val);PreOrder(root->_left);PreOrder(root->_right);
}
void InOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}InOrder(root->_left);printf("%d ", root->val);InOrder(root->_right);
}
void PostOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%d ", root->val);
}//节点个数
int Treesize(BTNode* root)
{return root == NULL ? 0 : 1 + Treesize(root->_left) + Treesize(root->_right);
}//叶子结点
int Treeleafsize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return Treeleafsize(root->_left) + Treeleafsize(root->_right);
}
//第K层结点个数
int TreeKlevelsize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKlevelsize(root->_left, k - 1) + TreeKlevelsize(root->_right, k-1);
}
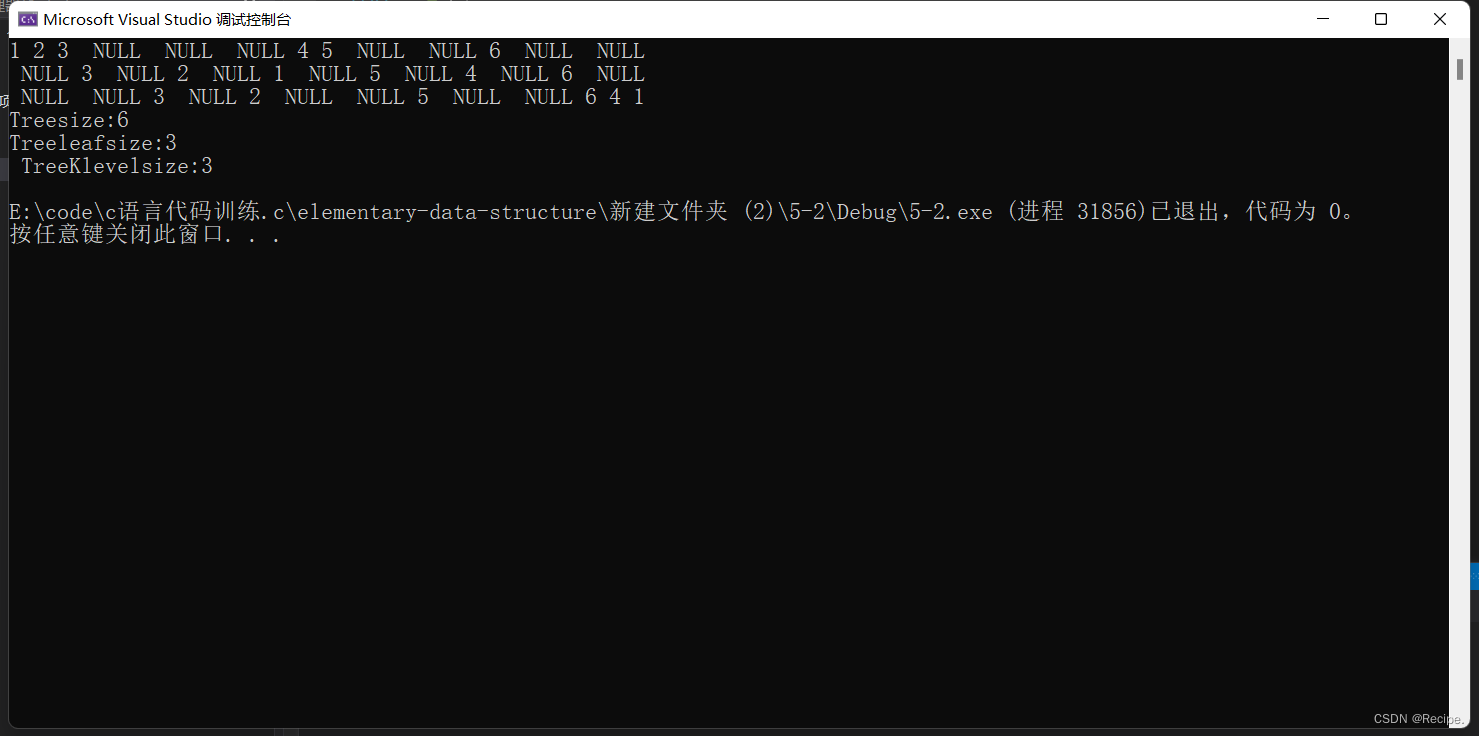
int main()
{BTNode* newnode1 = buynode(1);BTNode* newnode2 = buynode(2);BTNode* newnode3 = buynode(3);BTNode* newnode4 = buynode(4);BTNode* newnode5 = buynode(5);BTNode* newnode6 = buynode(6);newnode1->_left = newnode2;newnode2->_left = newnode3;newnode1->_right = newnode4;newnode4->_left = newnode5;newnode4->_right = newnode6;PreOrder(newnode1);printf("\n");InOrder(newnode1);printf("\n");PostOrder(newnode1);printf("\n");printf("Treesize:%d\n", Treesize(newnode1));printf("Treeleafsize:%d\n", Treeleafsize(newnode1));printf(" TreeKlevelsize:%d\n", TreeKlevelsize(newnode1,3));return 0;
}
相关文章:

数据结构——二叉树链式结构的实现(上)
二叉树概念 再看二叉树基本操作前,再回顾下二叉树的概念, 二叉树是: 1. 空树 2. 非空:根节点,根节点的左子树、根节点的右子树组成的。 从概念中可以看出,二叉树定义是递归式的 二叉树构成࿱…...

数据结构内容概览
0. 绪论 绪论01——复杂度度量 绪论02——复杂度分析 绪论03——递归分析 绪论04——算法分析 绪论05——动态规划 算法设计与优化——前n项和计算 算法设计优化——对于任意非负整数,统计其二进制展开中数位1的总数 算法设计优化——Fibonacci数 算法设计优化——…...

当Linux系统运行时间长了之后,会出现磁盘空间不足提示,需要及时进行清理
Linux系统(CentOS 7)的磁盘空间不足时,可以采取以下步骤进行清理: 查找并删除大文件: 使用du和find命令可以找到并删除大文件。例如,要查找/目录下大于100MB的文件,可以运行: find /…...

【Flask 系统教程 4】Jinjia2模版和语法
Jinjia2 模板 模板的介绍 Jinja2 是一种现代的、设计优雅的模板引擎,它是 Python 的一部分,由 Armin Ronacher 开发。Jinja2 允许你在 HTML 文档中嵌入 Python 代码,以及使用变量、控制结构和过滤器来动态生成内容。它的语法简洁清晰&#…...
与 Apollo 共创生态:七周年大会心得
与 Apollo 共创生态:七周年大会心得 前言 4月19日,百度Apollo迎来七周年,历经七年的不懈追求与创新,Apollo开放平台已陆续推出了13个版本,汇聚了来自全球170多个国家与地区的16万名开发者及220多家合作伙伴。作为一名…...

『FPGA通信接口』DDR(4)DDR3内存条SODIMMs读写测试
文章目录 前言1.MIG IP核配置2.测试程序3.DDR应用4.传送门 前言 不论是DDR3颗粒还是DDR3内存条,xilinx都是通过MIG IP核实现FPGA与DDR的读写。本文区别于DDR颗粒,记录几个与颗粒配置不同的地方。关于DDR的原理与MIG IP的简介,请查看前面文章&…...

Element UI 快速入门指南
Element UI 快速入门指南 Element UI 是一个基于 Vue.js 的组件库,提供了丰富的 UI 组件和工具,可以帮助开发人员快速构建现代化的 Web 应用程序。本文将介绍如何快速入门使用 Element UI,并展示一些常用的组件和功能。 安装 Element UI 使…...

CentOS常用命令有哪些?
目录 一、CentOS常用命令有哪些? 二、不熟悉命令怎么办? 场景一:如果是文件操作,可以使用FileZilla工具来完成 场景二:安装CentOS桌面 一、CentOS常用命令有哪些? CentOS 系统中有许多常用命令及其用法…...

cmd查看局域网内所有设备ip
说明:最近碰到一个新问题,就是有一个安卓设备,安装了一个app导致死机了,app设置了开机重启,所以,无论重启还是关机,都是进来就白屏, 这可把人愁坏了,直接死循环了 无论…...

5.3作业
这个声明定义了一个名为 s 的数组,数组包含 10 个元素,每个元素都是一个函数指针。(1)C (2)D (3)C (4)DE (5)C8 11 14(1)int IsFull(sequeue *seqn) { return ((seqn->frnt ((seqn->rear 1) % N)) ? 1 : 0); } (2)int IsEmpty(sequ…...

java-Spring-mvc-(请求和响应)
目录 📌HTTP协议 超文本传输协议 请求 Request 响应 Response 🎨请求方法 GET请求 POST请求 📌HTTP协议 超文本传输协议 HTTP协议是浏览器与服务器通讯的应用层协议,规定了浏览器与服务器之间的交互规则以及交互数据的格式…...

亚马逊测评工作室如何轻松实现高收益,跨境电商揭秘汇率差赚钱术
随着跨境电商在国内市场的持续繁荣,众多电商卖家纷纷将目光投向了这一充满活力的领域。面对国内市场的激烈竞争,许多卖家选择向外拓展,寻求更广阔的发展空间。其中,亚马逊成为了众多卖家的不二选择,毕竟老外的市场还是…...

unity中 UnityWebRequest.Post和 UnityWebRequest uwr = new UnityWebRequest两种方法有什么区别
在Unity中,UnityWebRequest.Post 和 UnityWebRequest uwr new UnityWebRequest(...) 是两种不同的方式来创建和发送HTTP POST请求,但它们之间有一些关键的区别和用法上的差异。 1. UnityWebRequest.Post (静态方法) UnityWebRequest.Post 是一个静态方…...

Java学习-练习试用Java实现求素数
以下是使用Java语言试着编写的求1-100内的素数的程序: public class PrimeNumbers {public static void main(String[] args) {System.out.println("Prime numbers between 1 and 100 are:");for (int i 2; i < 100; i) {if (isPrime(i)) {System.ou…...

最近学习发现一个background-blend-mode,这是CSS的一个新成员吧!这里分享记录一下
介绍 background-blend-mode CSS 属性定义该元素的背景图片,以及背景色如何混合。 混合模式应该按background-image CSS 属性同样的顺序定义。如果混合模式数量与背景图像的数量不相等,它会被截取至相等的数量。在所有的元素中。在SVG,它适…...
虚幻引擎5 Gameplay框架(二)
Gameplay重要类及重要功能使用方法(一) 配置LOG类及PlayerController的网络机制 探索验证GamePlay重要函数、类的执行顺序与含义 我们定义自己的日志,专门建立一个存放自己日志的类,这个类继承自BlueprintFunctionLibrary 然后…...
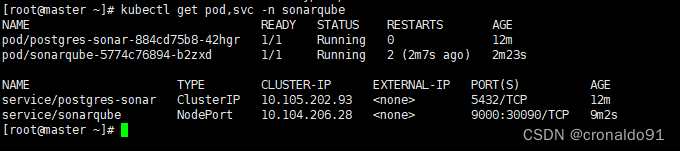
云原生Kubernetes: K8S 1.29版本 部署Sonarqube
一、实验 1.环境 (1)主机 表1 主机 主机架构版本IP备注masterK8S master节点1.29.0192.168.204.8 node1K8S node节点1.29.0192.168.204.9node2K8S node节点1.29.0192.168.204.10已部署Kuboard (2)master节点查看集群 1&…...
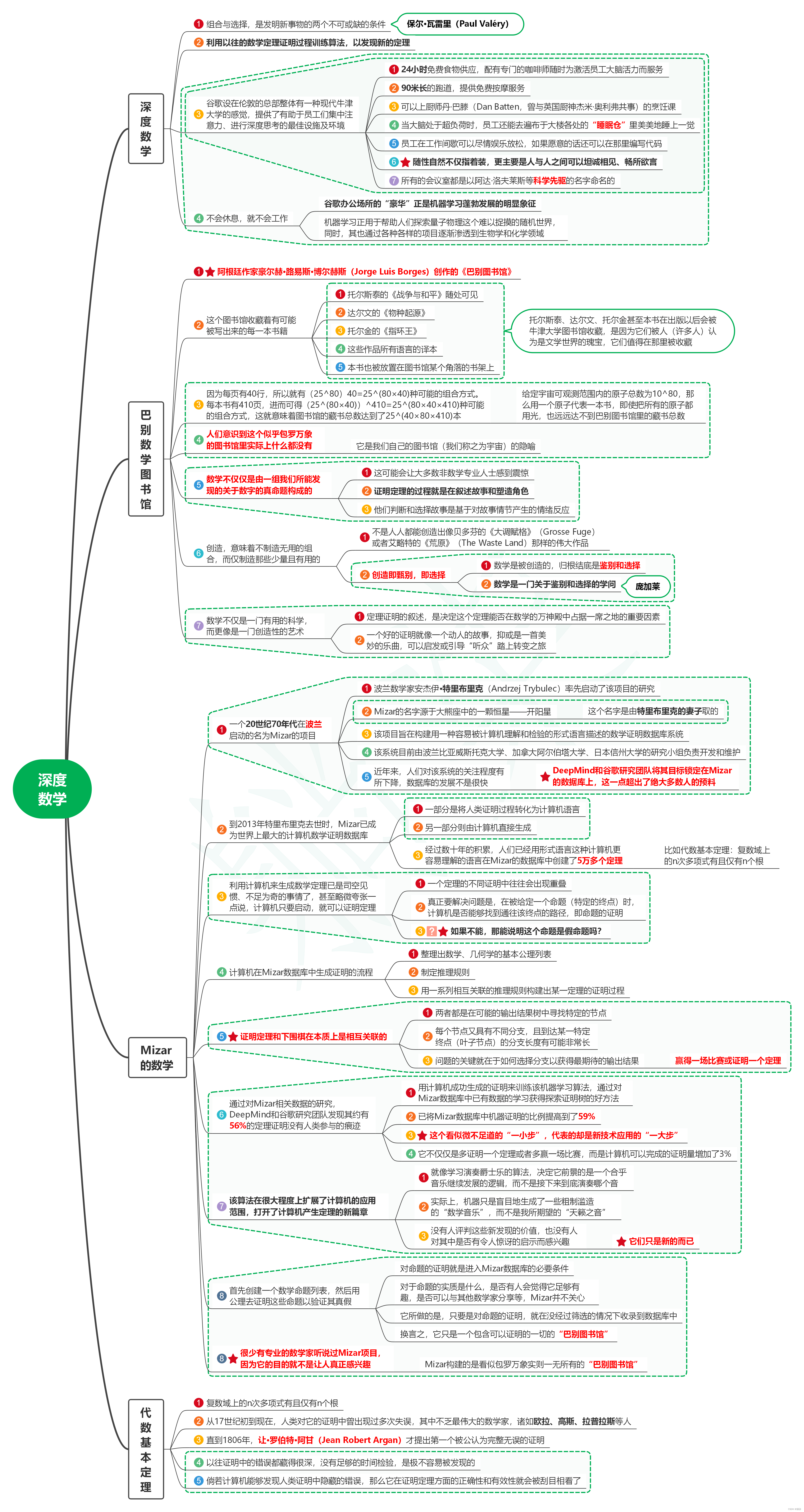
读天才与算法:人脑与AI的数学思维笔记19_深度数学
1. 深度数学 1.1. 组合与选择,是发明新事物的两个不可或缺的条件 1.1.1. 保尔瓦雷里(Paul Valry) 1.2. 利用以往的数学定理证明过程训练算法,以发现新的定理 1.3. 谷歌设在伦敦的总部整体有一种现代牛津大学的感觉,…...
Springboot+Vue项目-基于Java+MySQL的旅游网站系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...

Element UI 简介
Element UI是一个基于Vue.js的组件库,提供了一套丰富的可复用的组件,包括按钮、表单、弹框、表格、菜单等等。它的设计风格简洁大方,易于使用,能够帮助开发者快速构建现代化的Web应用。 在Element UI中,有许多常用的组…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
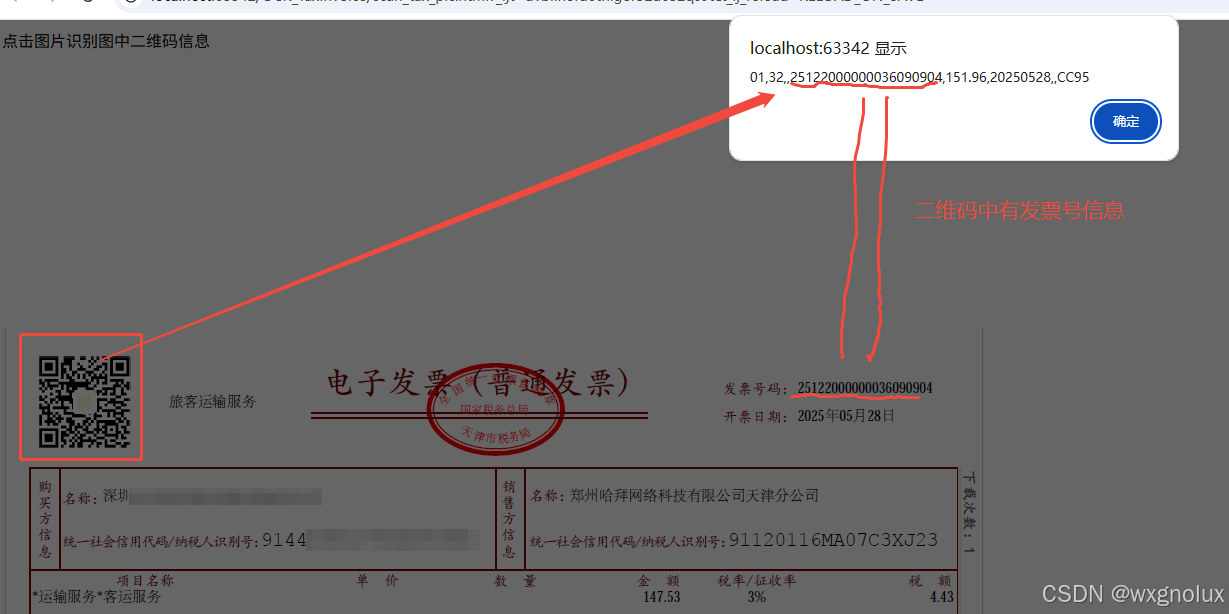
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...
