(图论)最短路问题合集(包含C,C++,Java,Python,Go)
不存在负权边:
1.朴素dijkstra算法
原题:

思路:(依然是贪心的思想)
1.初始化距离:dis[1]=0,dis[i]=INF(正无穷)
2.循环n次:
找到当前不在s中的dis最小的点(s表示已经确定最短距离的点(可以开一个st数组表示))
假设找到了t这个点,用这个点更新其他所有点的最短距离:
if dis[x]>dis[t]+wi(这里wi表示边权)
实例演示:
代码如下:
一些注意细节(用//表示)
c++版本:
#include <iostream>
#include <cstring>using namespace std;
const int N=510;
int q[N][N];
int dis[N];
int n,m;
bool st[N];
int dijkstra(){memset(dis,0x3f,sizeof dis);dis[1]=0;for(int i=0;i<n-1;i++){int t=-1;for(int j=1;j<=n;j++){if(!st[j]&&(t==-1||dis[t]>dis[j])){
//这里t==-1,其实代表是第一次进入,更新t的值,而后面才开始比较t=j;}}for(int j=1;j<=n;j++){dis[j]=min(dis[j],dis[t]+q[t][j]);}st[t]=1;}if(dis[n]==0x3f3f3f3f) return -1;return dis[n];
}int main(){cin>>n>>m;memset(q,0x3f,sizeof q);while(m--){int x,y,z;cin>>x>>y>>z;q[x][y]=min(q[x][y],z);}cout<<dijkstra()<<" ";return 0;
}C:
#include <stdio.h>
#include <string.h>#define N 510int q[N][N];
int dis[N];
int n, m;
int st[N];int min(int a, int b) {return a < b ? a : b;
}int dijkstra() {memset(dis, 0x3f, sizeof(dis));dis[1] = 0;for (int i = 0; i < n - 1; i++) {int t = -1;for (int j = 1; j <= n; j++) {if (!st[j] && (t == -1 || dis[t] > dis[j])) {t = j;}}for (int j = 1; j <= n; j++) {dis[j] = min(dis[j], dis[t] + q[t][j]);}st[t] = 1;}if (dis[n] == 0x3f3f3f3f) return -1;return dis[n];
}int main() {scanf("%d %d", &n, &m);memset(q, 0x3f, sizeof(q));while (m--) {int x, y, z;scanf("%d %d %d", &x, &y, &z);q[x][y] = min(q[x][y], z);}printf("%d ", dijkstra());return 0;
}
python:
import sys N = 510
q = [[float('inf')] * N for _ in range(N)] # 初始化邻接矩阵
dis = [float('inf')] * N # 初始化距离数组
st = [False] * N # 初始化标记数组 n, m = map(int, input().split()) # 读取节点数和边数 # 读取边的信息
for _ in range(m): x, y, z = map(int, input().split()) q[x - 1][y - 1] = min(q[x - 1][y - 1], z) # 注意索引从0开始 def dijkstra(): dis[0] = 0 # 起始节点距离设为0 for _ in range(n - 1): t = -1 for j in range(n): if not st[j] and (t == -1 or dis[j] < dis[t]): t = j for j in range(n): if q[t][j] != float('inf'): dis[j] = min(dis[j], dis[t] + q[t][j]) st[t] = True if dis[n - 1] == float('inf'): return -1 return dis[n - 1] print(dijkstra())Go:
package main import ( "bufio" "fmt" "math" "os" "strconv" "strings"
) const N = 510 var ( q [N][N]int dis [N]int n int m int st = make([]bool, N)
) func min(a, b int) int { if a < b { return a } return b
} func dijkstra() int { for i := range dis { dis[i] = math.MaxInt32 } dis[0] = 0 // 注意Go的数组索引从0开始 for i := 0; i < n; i++ { t := -1 for j := 0; j < n; j++ { if !st[j] && (t == -1 || dis[j] < dis[t]) { t = j } } for j := 0; j < n; j++ { if q[t][j] != math.MaxInt32 { dis[j] = min(dis[j], dis[t]+q[t][j]) } } st[t] = true } if dis[n-1] == math.MaxInt32 { return -1 // 如果没有路径到达节点n-1 } return dis[n-1]
} func main() { scanner := bufio.NewScanner(os.Stdin) fmt.Scanln(&n, &m) for i := range q { for j := range q[i] { q[i][j] = math.MaxInt32 } } for m > 0 { m-- scanner.Scan() line := scanner.Text() fields := strings.Fields(line) x, _ := strconv.Atoi(fields[0]) y, _ := strconv.Atoi(fields[1]) z, _ := strconv.Atoi(fields[2]) x-- // 转换为Go的索引 y-- q[x][y] = min(q[x][y], z) } fmt.Println(dijkstra())
}这里储存方式用邻接矩阵,主要是因为用于稠密图。图中可能存在重边和自环,但所有边权均为正值。算法复杂度:
2.堆优化的dijkstra
我们思考一下,上述步骤在哪里可以优化:找到当前不在s中的dis最小的点,我们可以用堆进行优化,优化后复杂度为:
,堆优化,手写堆和优先队列,但是其实在dijkstra中,不需要手写堆,两个复杂度差不多,不如用优先队列方便。并且,此时为稀疏图,用邻接表更好。
我们用邻接表现在只需要遍历邻接表中头元素连接的,进行更改,每一次取出队列中的最小值即可
C++:
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1e6 + 10;//注意开两倍大小
int h[N], w[N], e[N], ne[N], idx;
int n,m;
int dis[N];
bool st[N];
typedef pair<int,int> PII;
priority_queue<PII,vector<PII>,greater<PII>> p;
void add(int a, int b, int c)//模板,记下来就好了
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra(){memset(dis,0x3f,sizeof dis);dis[1]=0;p.push({0,1});while(p.size()){auto t=p.top();p.pop();int ver=t.second;if(st[ver]) continue;//判断是否之前更新过了st[ver]=1;for(int i=h[ver];i!=-1;i=ne[i]){int j=e[i];if(dis[j]>dis[ver]+w[i]){dis[j]=dis[ver]+w[i];p.push({dis[j],j});}}}if(dis[n]==0x3f3f3f3f) return -1;return dis[n];
}int main(){cin>>n>>m;memset(h, -1, sizeof h);//邻接表记得初始化头结点while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}cout<<dijkstra()<<" ";return 0;
}python:
import heapqN = 1000010
h = [-1] * N
w = [0] * N
e = [0] * N
ne = [0] * N
idx = 0
n, m = map(int, input().split())
dis = [float('inf')] * N
st = [False] * N
p = []def add(a, b, c):global idxe[idx] = bw[idx] = cne[idx] = h[a]h[a] = idxidx += 1def dijkstra():global disdis[1] = 0heapq.heappush(p, (0, 1))while p:d, ver = heapq.heappop(p)if st[ver]:continuest[ver] = Truei = h[ver]while i != -1:j = e[i]if dis[j] > dis[ver] + w[i]:dis[j] = dis[ver] + w[i]heapq.heappush(p, (dis[j], j))i = ne[i]if dis[n] == float('inf'):return -1return dis[n]for _ in range(m):a, b, c = map(int, input().split())add(a, b, c)print(dijkstra())
如果存在负权边:
3.bellman-ford

对于边的存储方式不高。故可以用结构体初始化。
方式:初始化所有点到源点的距离为∞,把源点到自己的距离设置为0,遍历n次;每次遍历m条边,用每一条边去更新各点到源点的距离。在碰到限制了最短路径上边的长度时就只能用bellman_ford了。
for n次
for 所有边 a,b,w (松弛操作)
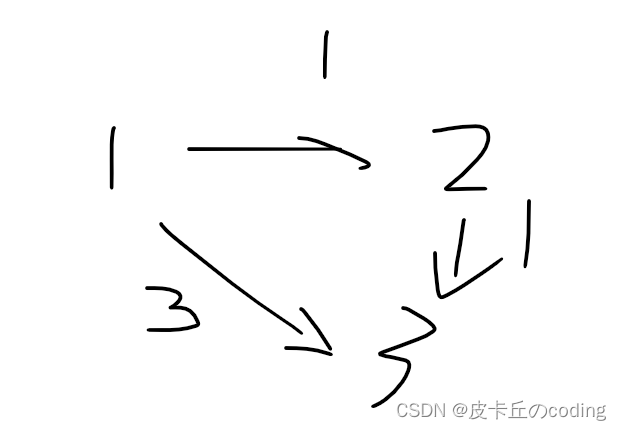
dis[b] = min(dis[b],back[a] + w)//注意:这里的backup非常重要,为了防止串联:(假设限制只能用1条边)
如下图:如果出现这样,不用之前的备份,就会出现1->3最近为2,而不是3,所以要备份一下之前的情况,用之前未更新的情况更新下一个节点。
c++:
#include<iostream>
#include <cstring>using namespace std;
const int N=510,M=10010;
struct edge{int a;int b;int w;
}edge[M];
int dis[N];
int backup[N];
int n,m,k;
void bellman_ford(){memset(dis,0x3f,sizeof dis);dis[1]=0;for(int i=0;i<k;i++){memcpy(backup,dis,sizeof dis);for(int j=0;j<m;j++){auto e=edge[j];dis[e.b]=min(dis[e.b],backup[e.a]+e.w);}}
}int main(){cin>>n>>m>>k;for(int i=0;i<m;i++){int x,y,z;cin>>x>>y>>z;edge[i]={x,y,z};
}bellman_ford();if(dis[n]>0x3f3f3f3f/2) puts("impossible");//可能存在负权边else printf("%d\n", dis[n]);return 0;
}c:
#include <stdio.h>
#include <string.h>#define N 510
#define M 10010struct Edge {int a;int b;int w;
};struct Edge edge[M];
int dis[N];
int backup[N];
int n, m, k;void bellman_ford() {memset(dis, 0x3f, sizeof dis);dis[1] = 0;for (int i = 0; i < k; i++) {memcpy(backup, dis, sizeof dis);for (int j = 0; j < m; j++) {struct Edge e = edge[j];if (backup[e.a] + e.w < dis[e.b]) {dis[e.b] = backup[e.a] + e.w;}}}
}int main() {scanf("%d %d %d", &n, &m, &k);for (int i = 0; i < m; i++) {int x, y, z;scanf("%d %d %d", &x, &y, &z);edge[i].a = x;edge[i].b = y;edge[i].w = z;}bellman_ford();if (dis[n] > 0x3f3f3f3f / 2) {printf("impossible\n");} else {printf("%d\n", dis[n]);}return 0;
}
python:
N = 510
M = 10010class Edge:def __init__(self, a, b, w):self.a = aself.b = bself.w = wedge = [Edge(0, 0, 0) for _ in range(M)]
dis = [float('inf')] * N
backup = [0] * Ndef bellman_ford():global disdis[1] = 0for _ in range(k):backup[:] = dis[:]for j in range(m):e = edge[j]dis[e.b] = min(dis[e.b], backup[e.a] + e.w)def main():global n, m, kn, m, k = map(int, input().split())for i in range(m):x, y, z = map(int, input().split())edge[i] = Edge(x, y, z)bellman_ford()if dis[n] > 0x3f3f3f3f // 2:print("impossible")else:print(dis[n])if __name__ == "__main__":main()
Go:
package mainimport ("fmt"
)const N = 510
const M = 10010type Edge struct {a, b, w int
}var edge [M]Edge
var dis [N]int
var backup [N]int
var n, m, k intfunc bellmanFord() {for i := range dis {dis[i] = 0x3f3f3f3f}dis[1] = 0for i := 0; i < k; i++ {copy(backup[:], dis[:])for j := 0; j < m; j++ {e := edge[j]if dis[e.b] > backup[e.a]+e.w {dis[e.b] = backup[e.a] + e.w}}}
}func main() {fmt.Scan(&n, &m, &k)for i := 0; i < m; i++ {var x, y, z intfmt.Scan(&x, &y, &z)edge[i] = Edge{x, y, z}}bellmanFord()if dis[n] > 0x3f3f3f3f/2 {fmt.Println("impossible")} else {fmt.Println(dis[n])}
}
时间复杂度:
4.spfa

对bellman-ford的优化,不一定每条边都会更新(spfa算法的想法基础)。
dis[b] = min(dis[b],back[a] + w)
观察这个式子,只有back[a]变小了,我的后继dis[b]才会变小
所以,我可以用一个队列,在一次变化中,只要有节点变小了,那么就肯定会影响后继节点,就放入队列之中。只要队列不空,就一直类似于bfs一样进行。
时间复杂度:一般,最坏
//与dijkstra非常相似
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>using namespace std;const int N = 100010;int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dis[N];
bool st[N];
queue<int> q;
void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}int spfa(){memset(dis,0x3f,sizeof dis);dis[1]=0;q.push(1);st[1]=1;while(q.size()){auto t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dis[j]>dis[t]+w[i]){dis[j]=dis[t]+w[i];if(!st[j]){q.push(j);st[j]=1;}}}}
return dis[n];
}
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof h);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = spfa();if (t == 0x3f3f3f3f) puts("impossible");else printf("%d\n", t);return 0;
}c:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h> #define N 100010
#define INF 0x3f3f3f3f int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dis[N];
bool st[N]; typedef struct { int data;
} QueueNode; typedef struct { QueueNode q[N]; int front, rear;
} Queue; void initQueue(Queue *q) { q->front = q->rear = 0;
} bool isEmpty(Queue *q) { return q->front == q->rear;
} void enqueue(Queue *q, int x) { q->q[q->rear].data = x; q->rear = (q->rear + 1) % N; // 使用循环队列防止溢出
} int dequeue(Queue *q) { if (isEmpty(q)) return -1; // 队列为空,返回错误标识 int x = q->q[q->front].data; q->front = (q->front + 1) % N; return x;
} void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
} int spfa() { memset(dis, INF, sizeof(dis)); dis[1] = 0; Queue q; initQueue(&q); enqueue(&q, 1); st[1] = true; while (!isEmpty(&q)) { int t = dequeue(&q); st[t] = false; for (int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; if (dis[j] > dis[t] + w[i]) { dis[j] = dis[t] + w[i]; if (!st[j]) { enqueue(&q, j); st[j] = true; } } } } return dis[n];
} int main() { scanf("%d%d", &n, &m); memset(h, -1, sizeof(h)); while (m--) { int a, b, c; scanf("%d%d%d", &a, &b, &c); add(a, b, c); } int t = spfa(); if (t == INF) printf("impossible\n"); else printf("%d\n", t); return 0;
}python:
from collections import dequeN = 100010n, m = map(int, input().split())
h = [-1] * N
w = [0] * N
e = [0] * N
ne = [0] * N
dis = [float('inf')] * N
st = [False] * N
q = deque()def add(a, b, c):global idxe[idx] = bw[idx] = cne[idx] = h[a]h[a] = idxidx += 1def spfa():global disdis[1] = 0q.append(1)st[1] = Truewhile q:t = q.popleft()st[t] = Falsei = h[t]while i != -1:j = e[i]if dis[j] > dis[t] + w[i]:dis[j] = dis[t] + w[i]if not st[j]:q.append(j)st[j] = Truei = ne[i]return dis[n]idx = 0
for _ in range(m):a, b, c = map(int, input().split())add(a, b, c)t = spfa()if t == float('inf'):print("impossible")
else:print(t)
5.spfa拓展:判断负环
原理:鸽笼原理+三角不等式
使用spfa算法解决是否存在负环问题
求负环的常用方法,基于SPFA,一般都用方法 2(该题也是用方法 2):
方法 1:统计每个点入队的次数,如果某个点入队n次,则说明存在负环
方法 2:统计当前每个点的最短路中所包含的边数,如果某点的最短路所包含的边数大于等于n,则也说明存在环
每次做一遍spfa()一定是正确的,但时间复杂度较高,可能会超时。初始时将所有点插入队列中可以按如下方式理解:
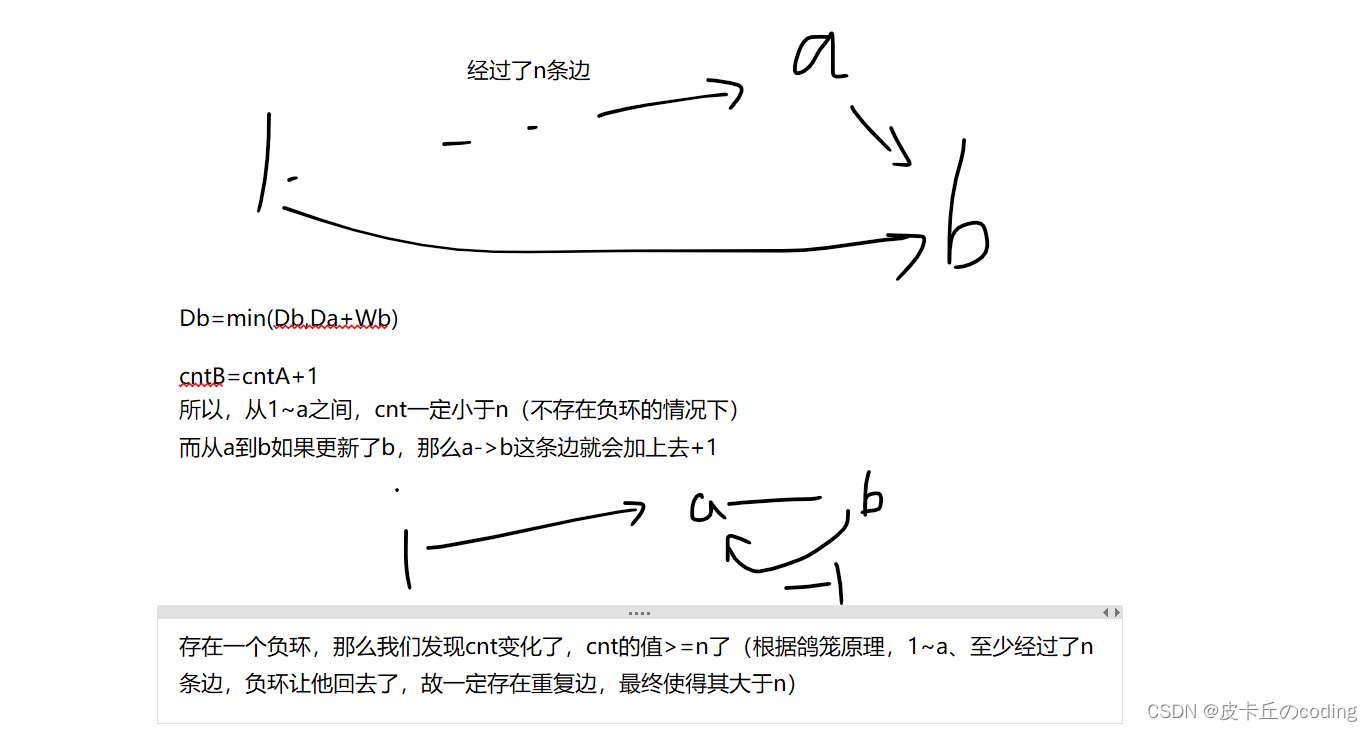
在原图的基础上新建一个虚拟源点,从该点向其他所有点连一条权值为0的有向边。那么原图有负环等价于新图有负环。此时在新图上做spfa,将虚拟源点加入队列中。然后进行spfa的第一次迭代,这时会将所有点的距离更新并将所有点插入队列中。执行到这一步,就等价于视频中的做法了。那么视频中的做法可以找到负环,等价于这次spfa可以找到负环,等价于新图有负环,等价于原图有负环。得证。1、dist[x] 记录虚拟源点到x的最短距离
2、cnt[x] 记录当前x点到虚拟源点最短路的边数,初始每个点到虚拟源点的距离为0,只要他能再走n步,即cnt[x] >= n,则表示该图中一定存在负环,由于从虚拟源点到x至少经过n条边时,则说明图中至少有n + 1个点,表示一定有点是重复使用
3、若dist[j] > dist[t] + w[i],则表示从t点走到j点能够让权值变少,因此进行对该点j进行更新,并且对应cnt[j] = cnt[t] + 1,往前走一步
注意:该题是判断是否存在负环,并非判断是否存在从1开始的负环,因此需要将所有的点都加入队列中,更新周围的点
引入一个cnt数组,记录每个点经过的边数
e.g.
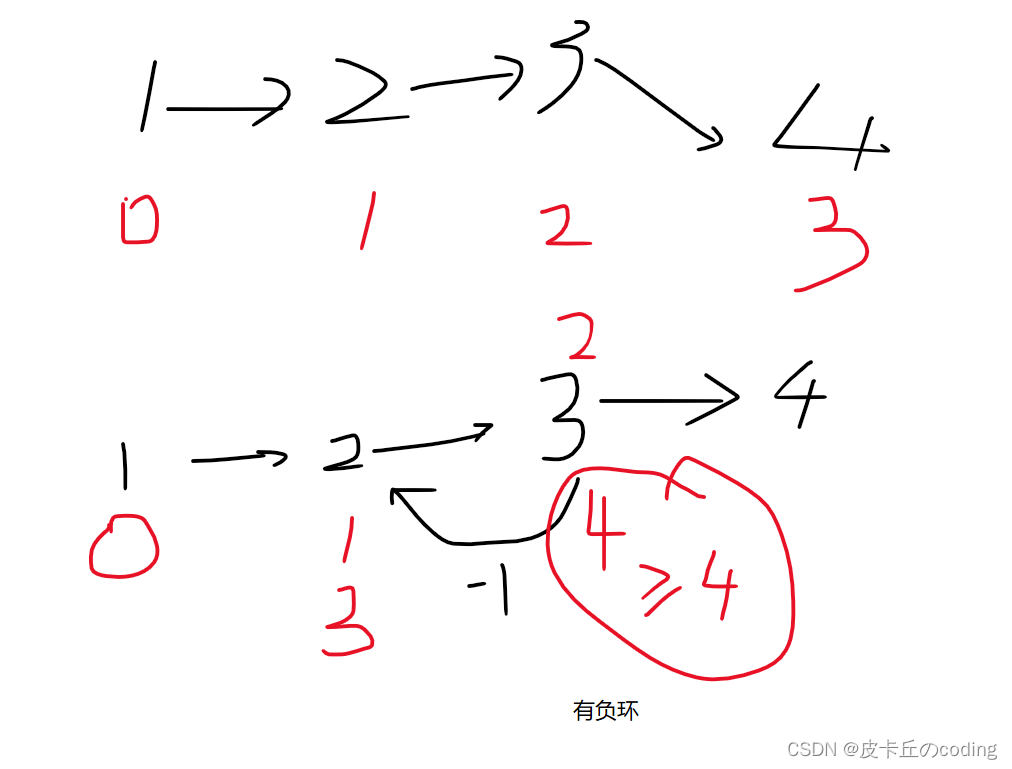
但是,如果从1开始到不了负环地方,那么就会出问题,我们的解决方法是一开始把所有的点都放入队列中:(本质就是以每个点为起点做一遍spfa)
for(int i=1;i<=n;i++){
st[i]=1;
q.push(i);
}
需要再cnt基础上更改的地方:
dis[j]=dis[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;还有对于cnt数组的初始化,还有把spfa变成布尔函数
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>using namespace std;const int N = 100010;int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dis[N];
int cnt[N];
bool st[N];
queue<int> q;
void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}bool spfa(){memset(dis,0x3f,sizeof dis);
for(int i=1;i<=n;i++){st[i]=1;q.push(i);
}dis[1]=0;q.push(1);st[1]=1;while(q.size()){auto t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(dis[j]>dis[t]+w[i]){dis[j]=dis[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n) return true;if(!st[j]){q.push(j);st[j]=1;}}}}
return false;
}
int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof h);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}
if(spfa()) puts("Yes");
else puts("No");return 0;
}多源汇最短路问题:
6.Floyd算法
原题:

原理:基于动态规划:
d[k,i,j]表示从第i个点出发到达j,只经过1~k个点的最短距离
状态转移方程:d[k,i,j]=d[k-1,i,k]+d[k-1,k,j]
发现:k与k-1刚好可以消去这个维度,用一个数组就可以实现
d[i,j]=d[i,k]+d[k,j]
算法时间复杂度:
具体:
假设节点序号是从1到n。
假设f[0][i][j]是一个n*n的矩阵,第i行第j列代表从i到j的权值,如果i到j有边,那么其值就为ci,j(边ij的权值)。
如果没有边,那么其值就为无穷大。f[k][i][j]代表(k的取值范围是从1到n),在考虑了从1到k的节点作为中间经过的节点时,从i到j的最短路径的长度。
比如,f[1][i][j]就代表了,在考虑了1节点作为中间经过的节点时,从i到j的最短路径的长度。
分析可知,f[1][i][j]的值无非就是两种情况,而现在需要分析的路径也无非两种情况,i->j,i->1->j:
【1】f[0][i][j]:i->j这种路径的长度,小于,i->1->j这种路径的长度
【2】f[0][i][1]+f[0][1][j]:i->1->j这种路径的长度,小于,i->j这种路径的长度
形式化说明如下:
f[k][i][j]可以从两种情况转移而来:
【1】从f[k−1][i][j]转移而来,表示i到j的最短路径不经过k这个节点
【2】从f[k−1][i][k]+f[k−1][k][j]转移而来,表示i到j的最短路径经过k这个节点总结就是:f[k][i][j]=min(f[k−1][i][j],f[k−1][i][k]+f[k−1][k][j])
从总结上来看,发现f[k]只可能与f[k−1]有关。
初始化与读入邻接矩阵(存在自环和重边的时候):
for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i == j) d[i][j] = 0;else d[i][j] = INF;while (m -- )
{int a, b, c;scanf("%d%d%d", &a, &b, &c);d[a][b] = min(d[a][b], c);
}
c++:
#include <iostream>
using namespace std;const int N = 210, INF = 1e9;int n, m, Q;
int d[N][N];
void floyd(){for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}
}
int main()
{scanf("%d%d%d", &n, &m, &Q);for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i == j) d[i][j] = 0;else d[i][j] = INF;while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);d[a][b] = min(d[a][b], c);}floyd();while (Q -- ){int a, b;scanf("%d%d", &a, &b);int t = d[a][b];if (t > INF / 2) puts("impossible");else printf("%d\n", t);}return 0;
}c:
#include <stdio.h>#define N 210
#define INF 1000000000int n, m, Q;
int d[N][N];void floyd() {for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (d[i][k] < INF && d[k][j] < INF) {int new_dist = d[i][k] + d[k][j];if (new_dist < d[i][j]) {d[i][j] = new_dist;}}}}}
}int main() {scanf("%d%d%d", &n, &m, &Q);for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) {d[i][j] = 0;} else {d[i][j] = INF;}}}while (m--) {int a, b, c;scanf("%d%d%d", &a, &b, &c);if (c < d[a][b]) {d[a][b] = c;}}floyd();while (Q--) {int a, b;scanf("%d%d", &a, &b);int t = d[a][b];if (t > INF / 2) {puts("impossible");} else {printf("%d\n", t);}}return 0;
}
java:
import java.util.Scanner;public class Main {static final int N = 210;static final int INF = 1000000000;static int n, m, Q;static int[][] d = new int[N][N];public static void floyd() {for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {d[i][j] = Math.min(d[i][j], d[i][k] + d[k][j]);}}}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();m = scanner.nextInt();Q = scanner.nextInt();for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) d[i][j] = 0;else d[i][j] = INF;}}while (m-- > 0) {int a = scanner.nextInt();int b = scanner.nextInt();int c = scanner.nextInt();d[a][b] = Math.min(d[a][b], c);}floyd();while (Q-- > 0) {int a = scanner.nextInt();int b = scanner.nextInt();int t = d[a][b];if (t > INF / 2) {System.out.println("impossible");} else {System.out.println(t);}}scanner.close();}
}
python:
import sysN = 210
INF = 10**9def floyd():global n, dfor k in range(1, n+1):for i in range(1, n+1):for j in range(1, n+1):d[i][j] = min(d[i][j], d[i][k] + d[k][j])if __name__ == "__main__":n, m, Q = map(int, input().split())d = [[INF for _ in range(N)] for _ in range(N)]for i in range(1, n+1):d[i][i] = 0for _ in range(m):a, b, c = map(int, input().split())d[a][b] = min(d[a][b], c)floyd()for _ in range(Q):a, b = map(int, input().split())t = d[a][b]if t > INF // 2:print("impossible")else:print(t)
Go语言:
package mainimport "fmt"const N = 210
const INF = 1000000000var n, m, Q int
var d [N][N]intfunc floyd() {for k := 1; k <= n; k++ {for i := 1; i <= n; i++ {for j := 1; j <= n; j++ {if d[i][k] < INF && d[k][j] < INF {newDist := d[i][k] + d[k][j]if newDist < d[i][j] {d[i][j] = newDist}}}}}
}func main() {fmt.Scanf("%d%d%d", &n, &m, &Q)for i := 1; i <= n; i++ {for j := 1; j <= n; j++ {if i == j {d[i][j] = 0} else {d[i][j] = INF}}}for m > 0 {var a, b, c intfmt.Scanf("%d%d%d", &a, &b, &c)if c < d[a][b] {d[a][b] = c}m--}floyd()for Q > 0 {var a, b intfmt.Scanf("%d%d", &a, &b)t := d[a][b]if t > INF/2 {fmt.Println("impossible")} else {fmt.Println(t)}Q--}
}
相关文章:
(图论)最短路问题合集(包含C,C++,Java,Python,Go)
不存在负权边: 1.朴素dijkstra算法 原题: 思路:(依然是贪心的思想) 1.初始化距离:dis[1]0,dis[i]INF(正无穷) 2.循环n次: 找到当前不在s中的dis最小的点&…...
电脑文件批量重命名不求人:快速操作,高效技巧让你轻松搞定
在数字化时代,电脑文件的管理与整理显得尤为重要。当面对大量需要重命名的文件时,一个个手动修改不仅耗时,还容易出错。那么,有没有一种方法可以快速、高效地完成这一任务呢?答案是肯定的,下面就来介绍几种…...

基于springboot的网上点餐系统源码数据库
基于springboot的网上点餐系统源码数据库 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身的优势;对于网上点餐系统当然也不能排除在外,随着网络技术的不断成熟,带动了网上点餐系统…...
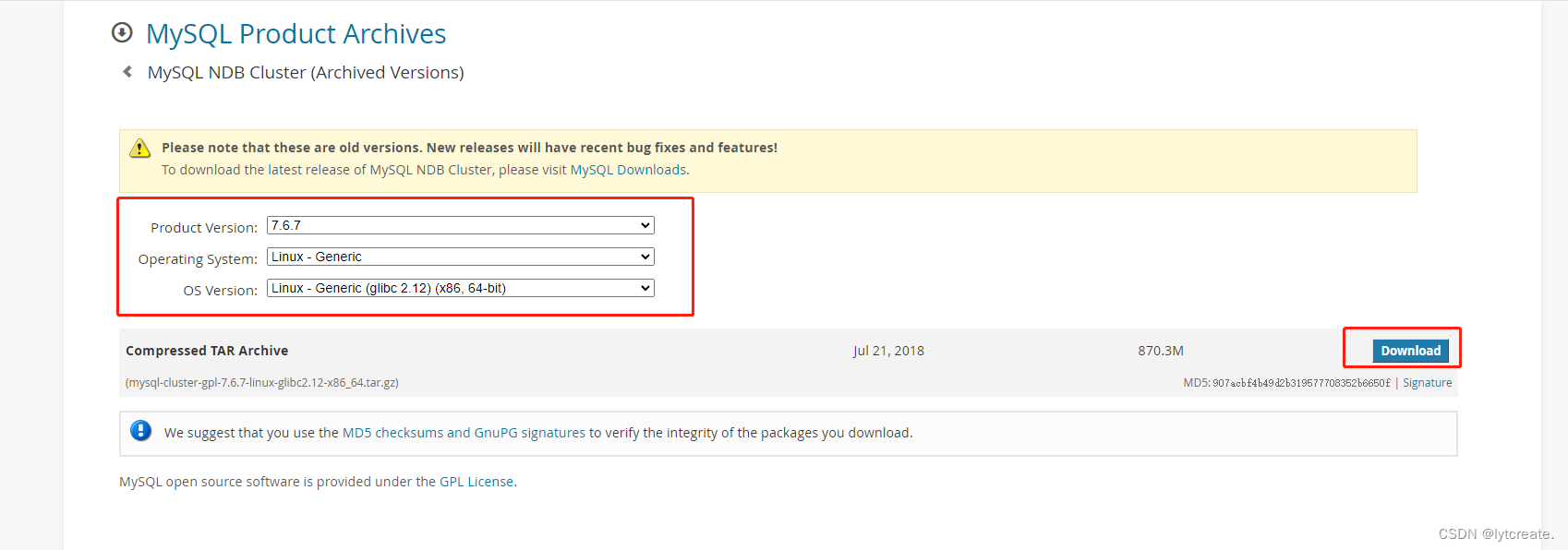
mysql cluster数据库集群介绍、部署及配置
前言: MySQL集群是一个无共享的、分布式节点架构的存储方案,旨在提供容错性和高性能。它由三个主要节点组成:管理节点(MGM)、数据节点和SQL节点。 管理节点(MGM) 定义与用途:管理节点是MySQL Cluster的控制中心,负责管理集群内的其他节点。它提供配置数据,启动和停止…...

uniapp的app端软件更新弹框
1:使用html PLUS实现:地址HTML5 API Reference (html5plus.org),效果图 2:在app.vue的onLaunch生命周期中,代码如下: onLaunch: function() {let a 0let view new plus.nativeObj.View(maskView, {backg…...
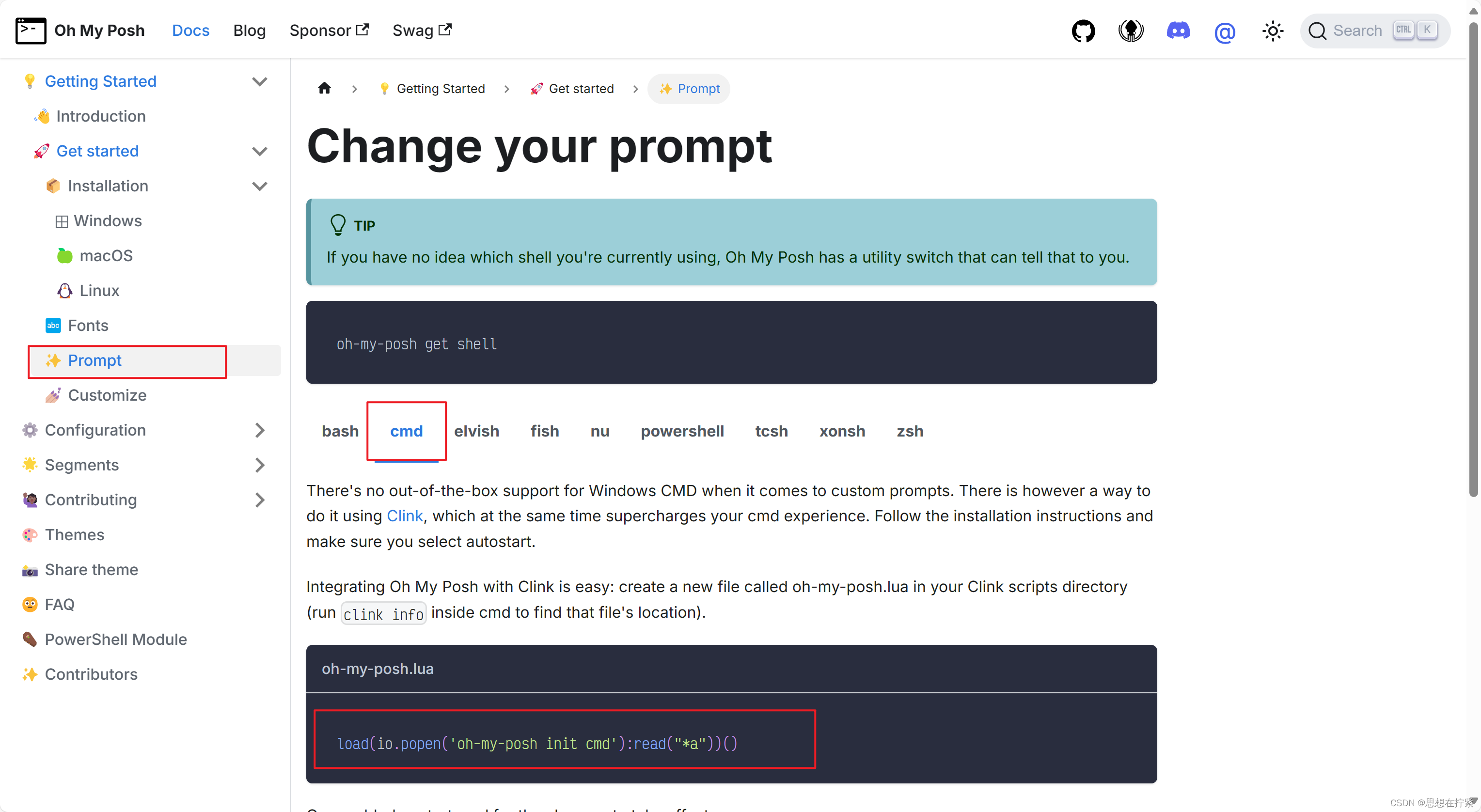
win11 Terminal 部分窗口美化
需求及分析:因为在 cmd、anaconda prompt 窗口中输入命令较多,而命令输入行和输出结果都是同一个颜色,不易阅读,故将需求定性为「美化窗口」。 美化结束后,我在想是否能不安装任何软件,简单地通过调整主题颜…...
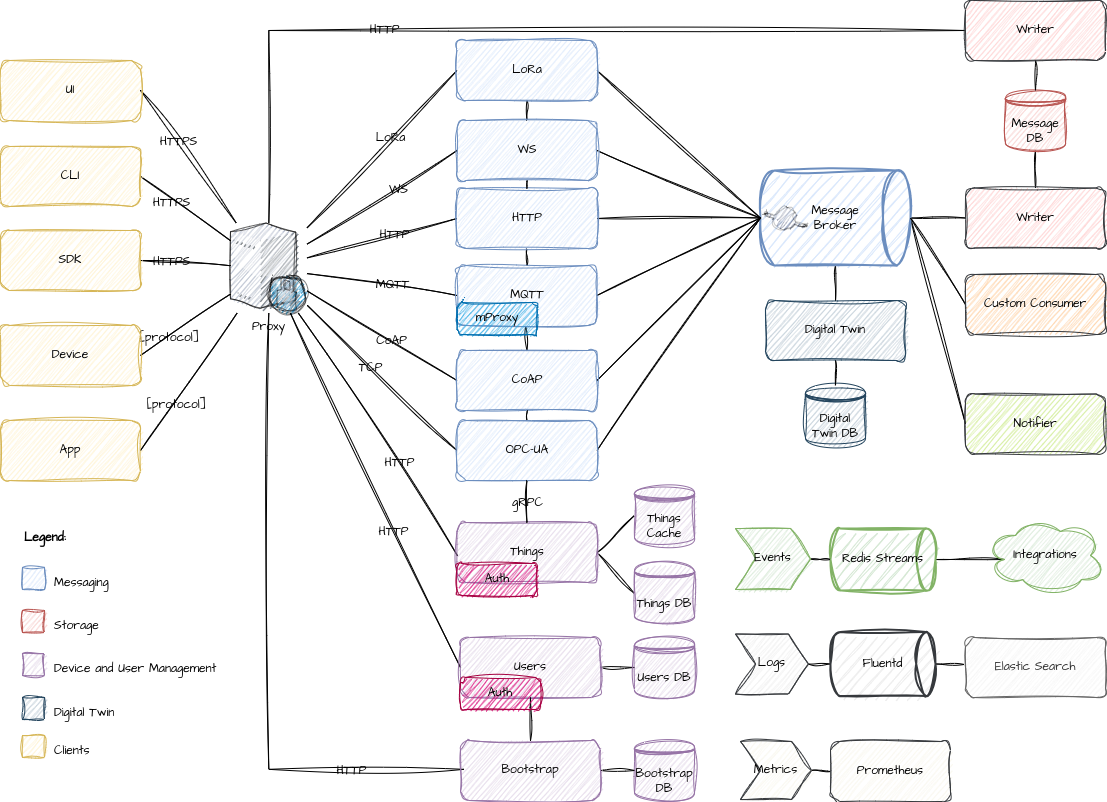
开源go实现的iot物联网新基建平台
软件介绍 Magistrala IoT平台是由Abstract Machines公司开发的创新基础设施解决方案,旨在帮助组织和开发者构建安全、可扩展和创新的物联网应用程序。曾经被称为Mainflux的平台,现在已经开源,并在国际物联网领域受到广泛关注。 功能描述 多协…...
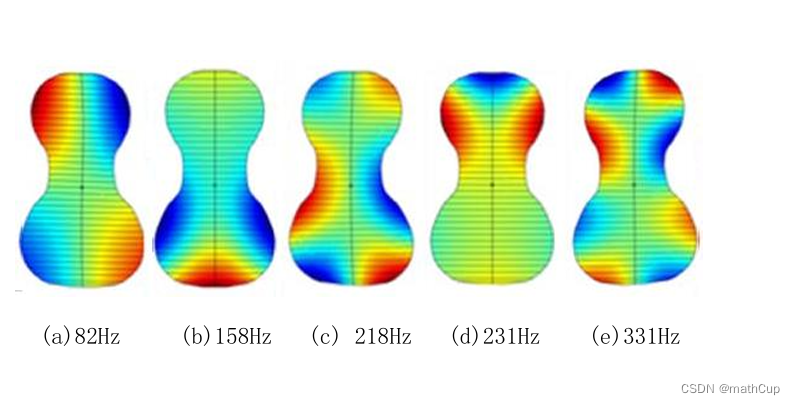
24深圳杯ABCD成品论文47页+各小问代码+图表
A题多个火箭残骸的准确定位: A题已经更新完22页完整版论文+高清无水印照片+Python(MATLAB)代码简单麦麦https://www.jdmm.cc/file/2710544/ 问题1:单个残骸的音爆位置确定 建模思路: 1. 声波传…...

doris经典bug
在部署完登录web页面查看的时候会发现只有一个节点可以读取信息剩余的节点什么也没读取到 在发现问题后,我们去对应的节点去看log日志,发现它自己绑定到前端的地址上了 现在我们已经发现问题了,以下就开始解决问题 重置doris 首先对be进行操…...
贪心算法应用例题
最优装载问题 #include <stdio.h> #include <algorithm>//排序int main() {int data[] { 8,20,5,80,3,420,14,330,70 };//物体重量int max 500;//船容最大总重量int count sizeof(data) / sizeof(data[0]);//物体数量std::sort(data, data count);//排序,排完数…...

亚信科技精彩亮相2024中国移动算力网络大会,数智创新共筑“新质生产力”
4月28至29日,江苏省人民政府指导、中国移动通信集团有限公司主办的2024中国移动算力网络大会在苏州举办。大会以“算力网络点亮AI时代”为主题,旨在凝聚生态伙伴合力,共同探索算力网络、云计算等数智能力空间,共促我国算网产业和数…...

图像处理中的颜色空间转换
在图像处理中,颜色空间转换是指将图像从一种颜色表示方式转换为另一种颜色表示方式。常见的颜色空间转换包括RGB到HSV、RGB到灰度、RGB到CMYK等。 RGB到HSV转换: RGB颜色空间由红色(R)、绿色(G)和蓝色&…...
网络安全之静态路由
以下是一个静态路由的拓扑图 Aping通B,C可以ping通D。 路由器转发数据需要路由表,但仍可以Aping通B,C可以ping通D,是因为产生了直连路由:产生的条件有两个,接口有IP,接口双up(物理upÿ…...

Golang | Leetcode Golang题解之第74题搜索二维矩阵
题目: 题解: func searchMatrix(matrix [][]int, target int) bool {m, n : len(matrix), len(matrix[0])i : sort.Search(m*n, func(i int) bool { return matrix[i/n][i%n] > target })return i < m*n && matrix[i/n][i%n] target }...

2023黑马头条.微服务项目.跟学笔记(五)
2023黑马头条.微服务项目.跟学笔记 五 延迟任务精准发布文章 1.文章定时发布2.延迟任务概述 2.1 什么是延迟任务2.2 技术对比 2.2.1 DelayQueue2.2.2 RabbitMQ实现延迟任务2.2.3 redis实现3.redis实现延迟任务4.延迟任务服务实现 4.1 搭建heima-leadnews-schedule模块4.2 数据库…...

C语言 | Leetcode C语言题解之第75题颜色分类
题目: 题解: void swap(int *a, int *b) {int t *a;*a *b, *b t; }void sortColors(int *nums, int numsSize) {int p0 0, p2 numsSize - 1;for (int i 0; i < p2; i) {while (i < p2 && nums[i] 2) {swap(&nums[i], &num…...

淘宝扭蛋机小程序开发:掌上惊喜,转出你的幸运宝藏
一、全新玩法,尽在掌中 淘宝扭蛋机小程序,将传统的扭蛋乐趣与数字时代完美结合,为您带来全新的购物体验。在这个小小的平台上,您可以用手指轻松操控,探索无尽的宝藏世界,转出专属于您的幸运好物。 二、海…...

Oracle索引组织表与大对象平滑迁移至OceanBase的实施方案
作者简介:严军(花名吉远),十年以上专注于数据库存储领域,精通Oracle、Mysql、OceanBase,对大数据、分布式、高并发、高性能、高可用有丰富的经验。主导过蚂蚁集团核心系统数据库升级,数据库LDC单元化多活项目ÿ…...
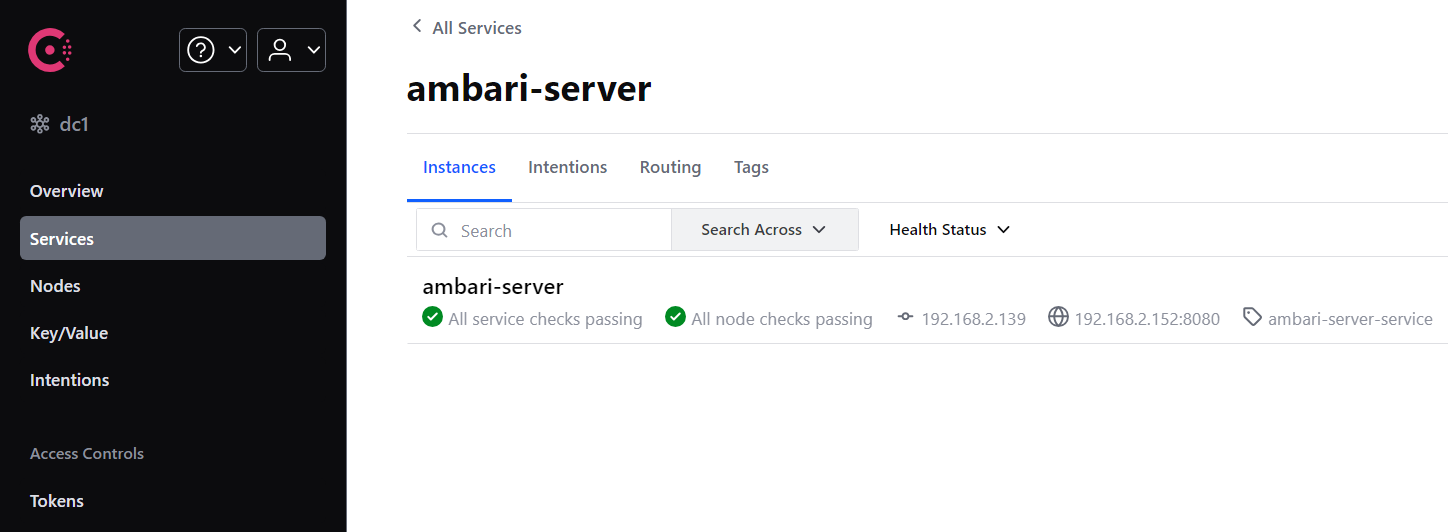
【服务治理中间件】consul介绍和基本原理
目录 一、CAP定理 二、服务注册中心产品比较 三、Consul概述 3.1 什么是Consul 3.2 Consul架构 3.3 Consul的使用场景 3.4 Consul健康检查 四、部署consul集群 4.1 服务器部署规划 4.2 下载解压 4.3 启动consul 五、服务注册到consul 一、CAP定理 CAP定理ÿ…...

无人机运营合格证:民用无人机驾驶航空器运营合格证书
无人机运营合格证是指经国家相关部门审核通过并颁发给相应无人驾驶航空器运营机构的一种资质证明。获得该证书的机构具备相关的技术和管理能力,能够安全、合规地运营无人驾驶航空器。 无人机运营合格证的申请流程一般包括报名、培训学习、考试准备、考试报名、考试…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
