密室逃脱游戏-第12届蓝桥杯省赛Python真题精选

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第58讲。
密室逃脱游戏,本题是2021年4月24日举办的第12届蓝桥杯青少组Python编程省赛真题,第12届一共有两场省赛,这是第二场。题目要求计算在100间密室中,按照游戏规则进入M号密室有多少种路线方案。
先来看看题目的要求吧。
一.题目说明
提示信息:
有一个密室逃脱游戏,有100间密室连在一排。密室编号是从1开始连续排列一直排到第100间密室,如下图:

游戏规则:
1. 玩家初始位置在1号密室;
2. 每次玩家可以进入右边的一个密室,也可以跳过一个密室进入下个密室(如:当玩家当前在3号密室,他可以进入4号密室也可以进入5号密室);
3. 有毒气的密室不能进入需要避开。
编程实现:
给定三个正整数X,Y,M(X < Y < M ≤ 100),表示三个密室编号,X号密室和Y号密室有毒气泄漏,不能进入,玩家需要进入到M号密室。按照游戏规则进入M号密室有多少种路线方案。
例如:X = 2,Y = 4,M = 7,进入M号密室有2种路线方案,分别是1->3->5->6->7路线和1->3->5->7路线。
输入描述:
输入三个正整数X,Y,M(X < Y < M),X和Y表示有毒气密室编号,M表示需要进入的密室编号,且三个正整数之间以英文逗号隔开
输出描述:
输出进入M号密室有多少种路线方案
样例输入:
2,4,7
样例输出:
2
二.思路分析
这是一道算法题,考查的知识点涉及循环、递归、列表和斐波那契数列等。
题目所描述的场景看起来是不是有似曾相识的感觉,但是又感觉有点怪怪的?实际上,这就是斐波那契数列(兔子数列)的变种问题,其本质仍然是斐波那契数列。
还记得斐波那契数列的递推公式吗:
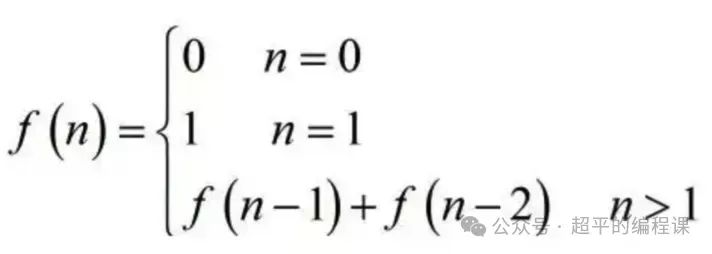
针对本题,我们可以运算分解思维将题目需求拆分成两步:
1). 假定没有毒气密室;
2). 增加X和Y两个毒气密室。
如果不考虑毒气密室,这就是我们熟悉的斐波那契数列,我们可以使用f(m)表示进入M号密室的路线数量。
当m = 3时,也就是3号密室,可以从1号密室过来,也可以从2号密室过来,根据加法原理,f(3) = f(1) + f(2)。
对于2号密室,它前面只有1号密室,因此路线数量为1,即f(2) = 1。
对于1号密室,它是玩家的初始位置,应该设置为多少呢?
如果只看1号密室本身,我们可以设置为0,也可以设置为1。但是从3号密室的角度来看,设置为1显然更合适。
所以,递推公式如下所示:
f(m) = 1 当m = 1 或 m = 2时f(m) = f(m - 1) + f(m - 2) 当m > 2时
如下图所示,这是在没有毒气密室时1~8号密室的路线数量:

接下来,我们再增加两个毒气密室X和Y,以题目给的样例数据X = 2,Y = 4,M = 7来说明。
X号密室和Y号密室有毒气泄漏,是不能进入的,这就意味着f(x)和f(y)都为0,即f(2) = f(4) = 0。
所以,在计算f(m)的时候,除了要单独考虑f(1)和f(2)之外,还需要考虑m = x、m = y的情况,如果 m = x 或者 m = y,那么f(m) = 0。
对应的,进入1~8号密室的路线数量如图所示:
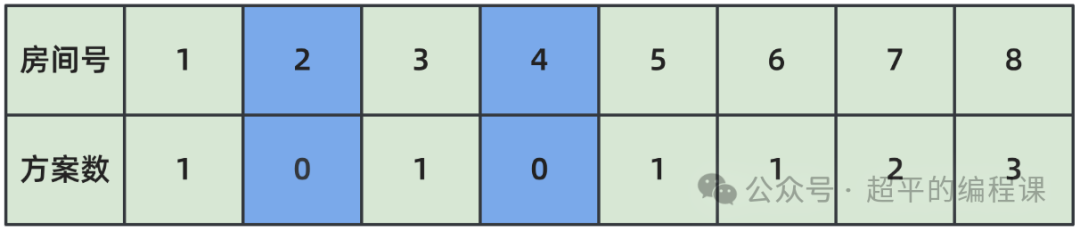
这就意味着在计算每个密室的路线数量时,需要判断房间号是否为x或y,递推公式如下:
f(m) = 0 当m = x 或 m = yf(m) = 1 当m = 1 或 m = 2f(m) = f(m - 1) + f(m - 2) 当m > 2时
针对斐波那契数列问题,通常有如下三种解决方案:
1). 递归
2). 动态规划
3). 迭代
这3种方案,都有一个共同点,那就是都需要用到递推公式。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们分别使用3种方案来编写程序:
-
递归
-
动态规划
-
递推
1. 递归
递归算法的核心是要定义递归函数,递归的3要素如下:
-
自定义函数,并且带有参数
-
在函数中调用自己
-
有结束条件
根据前面思路分析中的递推的公式,编写代码如下:
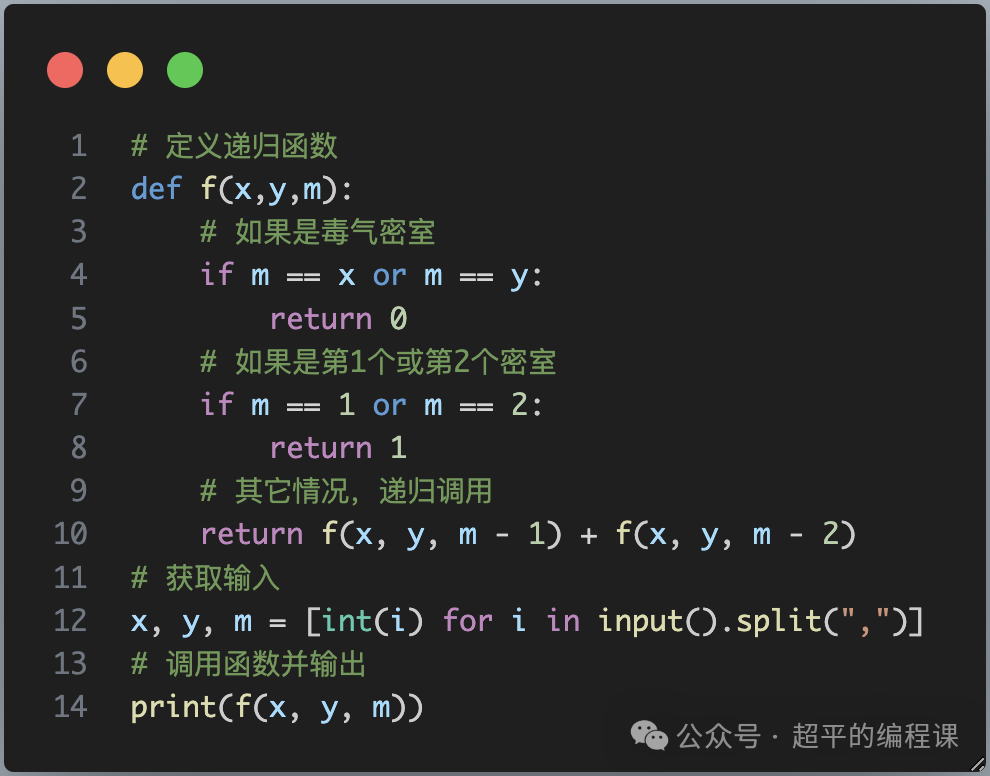
代码比较简单,这也是递归函数的特点,强调两点:
1). m = x或y的条件,要先于m == 1或2;
2). 在if语句中有return语句,因此不需要使用elif和else,代码更加简洁。
但是,这个代码是有问题的,如果m比较大的话,会存在超时的情况,你可以测试一下m为100的情况。
为什么会超时呢,原因在于进行了大量重复的计算,比如在计算f(x, y,10)的时候,需要计算f(x, y, 9)和f(x, y, 8),而在计算f(x, y, 9)的时候,需要计算f(x, y, 8)和f(x, y, 7),很显然,f(x, y, 8)计算了两次。
实际上,随着m的增加,计算的次数会以指数的形式增加。能否将这些已经计算过的值保存起来,从而避免重复计算呢。
这就是带备忘录的递归算法,可以增加一个列表,用于保存f(x, y, m)的值。
修改代码如下:
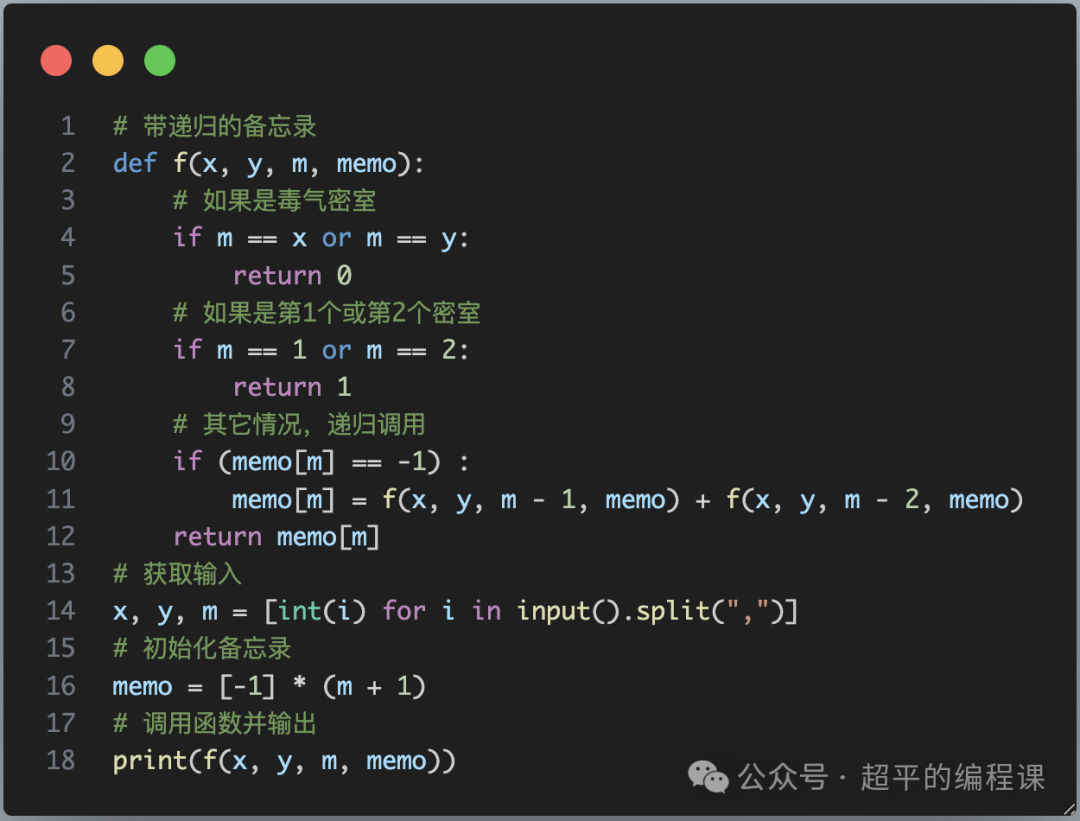
说明两点:
1). 递归函数中增加了一个参数memo,这就是备忘录列表;
2). 将列表的初始值设为-1,然后判断memo[m]的值,如果为-1,则说明是第一次计算,将计算的结果保存到memo列表中。
有了带备忘录的递归算法,时间复杂度将大大降低,效率会得到极大的提升,这是典型的用空间换时间的策略。
2. 动态规划
递归算法是自顶向下的策略,而动态规划则是自底向上的思想,可以从第1项和第2项开始,逐个计算后续的每一项。
动态规划有两个关键点:
-
定义dp列表
-
找出推导公式(状态转移方程)
我们可以定义dp[i]表示到i号密室的路线数量,由于列表的下标是从0开始的,为了方便,将dp[0]设为0,表示0号房间,可以理解为是虚拟的一个房间,dp[1]设置为1,表示1号房间,依此类推...
对应的代码如下:
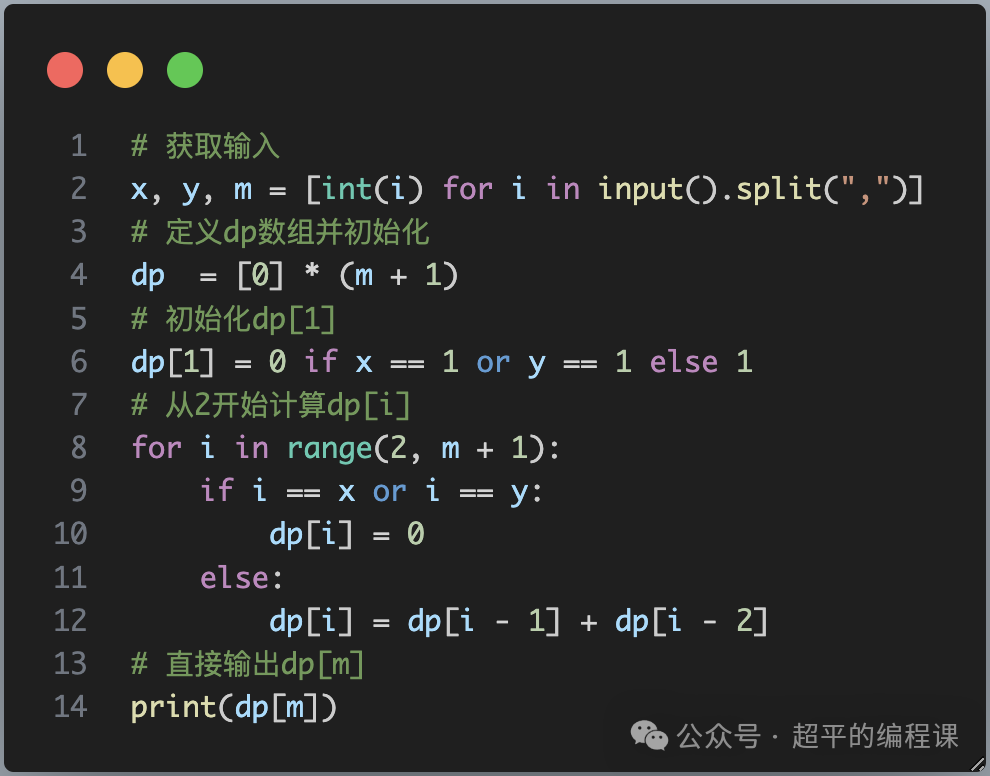
代码也不算多,说明两点:
1). 在计算dp[1]的时候,使用了带条件的赋值语句,这体现了Python的简洁性;
2). 虽然列表有第0项,但它是虚拟的,实际上我们是从第1项开始算的,即下标为1的列表项表示1号密室,因此对于m号密室,就是dp[m]。
3. 递推
仔细分析动态规划中的代码,可以发现在计算dp[i]的时候,实际上只用到了dp[i - 1]和dp[i - 2]。
于是,一些追求完美的同学开始有想法了,能否不用列表呢,这样还可以节省不少空间呢。
确实可以,实际上,我们只需要3个变量就够了,不妨用fm表示当前项,f2表示第m -1项,f1表示第m - 2项。
接下来使用循环从第3项开始,一步一步的计算每一项,这就是递推的算法思想,也叫迭代,对应的代码如下所示:

代码不多,说明两点:
1). 在计算第1项和第2项的时候,需要考虑x和y的取值;
2). 每次在计算好当前项fm的值后,需要重新设置f1和f2,可以理解为f1和f2都右移一位。
至此,整个程序就全部完成了,你也可以输入不同的数字来测试效果啦
四.总结与思考
本题代码在10行左右,涉及到的知识点包括:
-
循环语句,主要是for...in;
-
条件语句;
-
输入处理,尤其是多个数据的输入;
-
列表的使用;
-
带条件的赋值语句;
-
斐波那契数列;
作为本次省赛的倒数第二题,难度较大,难点在于如何找到突破点,将问题拆分成两个小问题,然后逐一解决。
将复杂问题拆分成多个简单问题,进而逐个解决,这是我们在学习编程时要重点培养和训练的一种思维。
任何复杂问题,只要能分解,我们就可以找到解决问题的方法。
号称硅谷钢铁侠的埃隆·马斯克曾经说过:“一个人最大的本事是拥有拆解思维,掌握它,你将活力四射”,由此可见,拆解思维是多么的强大和重要。
斐波那契数列,这是我们学习算法的必备经典问题,本文给出了3种解决方案,分别是递归、动态规划和递推(迭代)。相比较而言,递推算法是最优的,时间复杂度和空间复杂度都是最低的。
当我们彻底理解了斐波那契数列问题,就可以解决一系列相关题目,基本上都是它的变种问题。
超平老师给你留一道思考题,这里给出了动态规划的解决方案,你认为斐波那契数列是一个真正的DP问题吗,为什么呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
相关文章:

密室逃脱游戏-第12届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第58讲。 密室逃脱游戏&…...

ES6-自学01
调用方法读取文件:如果失败就throw抛出err,成功则抛出data 2.使用promise封装,如果失败就改变状态为 reject(err) 如果成功就 resolve(返回成功的值) ,然后then,就可以获取返回的值,值toString()方法来把…...

PyQt5批量生成Checkbox及批量检查Checkbox的勾选状态
批量生成Checkbox并添加到TableWidget中 for i in range(10):checkbox_i QCheckBox(fCheckbox_{i}) # 生成Checkbox并命名为Checkbox_iself.ui_1.tableWidget_1.setCellWidget(i,1,checkbox_i) 批量检查勾选状态 # 批量生成Checkbox并存入列表 list_Checkbox_1 [] for …...
如何获得一个Oracle 23ai数据库(Virtual Appliance)
准确的说,是Oracle 23ai Free Developer版,因为企业版目前只在云上(OCI和Azure)和ECC上提供。 方法包括3种,本文介绍第1种: Virtual ApplianceRPM安装Docker 从此处下载虚拟机。 可以看到虚拟机需要4G内…...

跟TED演讲学英文:What moral decisions should driverless cars make by Iyad Rahwan
What moral decisions should driverless cars make? Link: https://www.ted.com/talks/iyad_rahwan_what_moral_decisions_should_driverless_cars_make Speaker: Iyad Rahwan Date: September 2016 文章目录 What moral decisions should driverless cars make?Introduct…...
-规格化交互信息Metric)
【ITK配准】第七期 尺度(Metric)-规格化交互信息Metric
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 公众号:VTK忠粉 前言 本文分享ITK中的互信息Metric,即itk::ITK中的互信息Metric,即itk::MutualInformationImageToImageMetric ,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享…...

Python练习 20240508一次小测验
Python基础 10道基础练习题 1. 个人所得税计算器描述输入输出示例…...

桥梁施工污水需要哪些工艺设备
桥梁施工过程中产生的污水通常包含泥浆、油污、化学品残留等污染物。为了有效处理这些污水,确保施工现场的环境保护和合规性,通常需要以下工艺设备: 沉砂池:用于去除污水中的砂粒和其他重质无机物,减少对后续处理设备的…...

ADOP带你了解:长距离 PoE 交换机
您是否知道当今的企业需要的网络连接超出了传统交换机所能容纳的长度?这就是我们在长距离 PoE 交换机方面的专业化变得重要的地方。我们了解扩展网络覆盖范围的挑战,无论是在广阔的园区还是在多栋建筑之间。使用这些可靠的交换机,我们不仅可以…...

想要品质飞跃?找六西格玛培训公司就对了!
在当今复杂多变的市场环境中,企业的竞争早已不再是单一的价格或产品竞争,而是转向了对品质、效率和创新的全面追求。六西格玛,作为一种全球公认的质量管理方法论,正成为越来越多企业追求品质革命的重要工具。在这其中,…...

【工具】Office/WPS 插件|AI 赋能自动化生成 PPT 插件测评 —— 必优科技 ChatPPT
本文参加百度的有奖征文活动,更主要的也是借此机会去体验一下 AI 生成 PPT 的产品的现状,因此本文是设身处地从用户的角度去体验、使用这个产品,并反馈最真实的建议和意见,除了明确该产品的优点之外,也发现了不少缺陷和…...

4000定制网站,因为没有案例,客户走了
接到一个要做企业站点的客户,属于定制开发,预算4000看起来是不是还行的一个订单? 接单第一步:筛客户 从客户询盘的那一刻开始就要围绕核心要素:预算和工期,凡是不符合预期的一律放掉就好了,没必…...

内容安全(AV)
防病毒网关(AV)简介 基于网络侧 识别 病毒文件,工作范围2~7层。这里的网关指的是内网和外网之间的一个关口,在此进行病毒的查杀。在深信服中就有一个EDR设备,该设备就是有两种部署,一个部署在网关…...
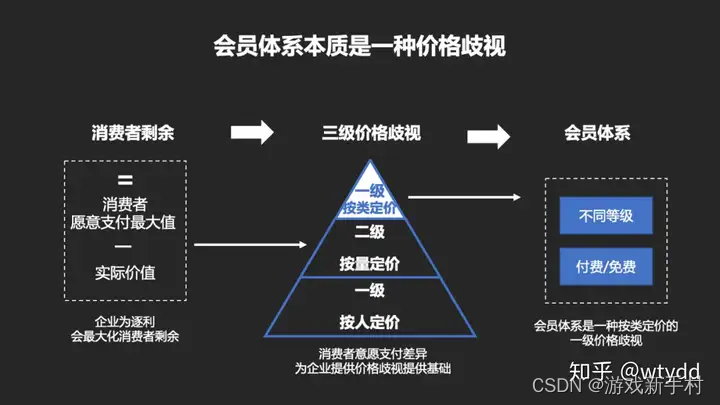
互联网产品为什么要搭建会员体系?
李诞曾经说过一句话:每个人都可以讲5分钟脱口秀。这句话换到会员体系里面同样适用,每个人都能聊点会员体系相关的东西。 比如会员体系属于用户运营的范畴,比如怎样用户分层,比如用户标签及CDP、会员积分、会员等级、会员权益和付…...

富格林:学习安全策略远离欺诈亏损
富格林悉知,黄金交易市场的每一分都可能发生变化。市场的波动会让很多人欢喜或沮丧,有人因此赚得盆满钵满,但也有人落入陷阱亏损连连,在现货黄金投资中,需要学习正规的做单技能,制定正规合理做单策略&#…...
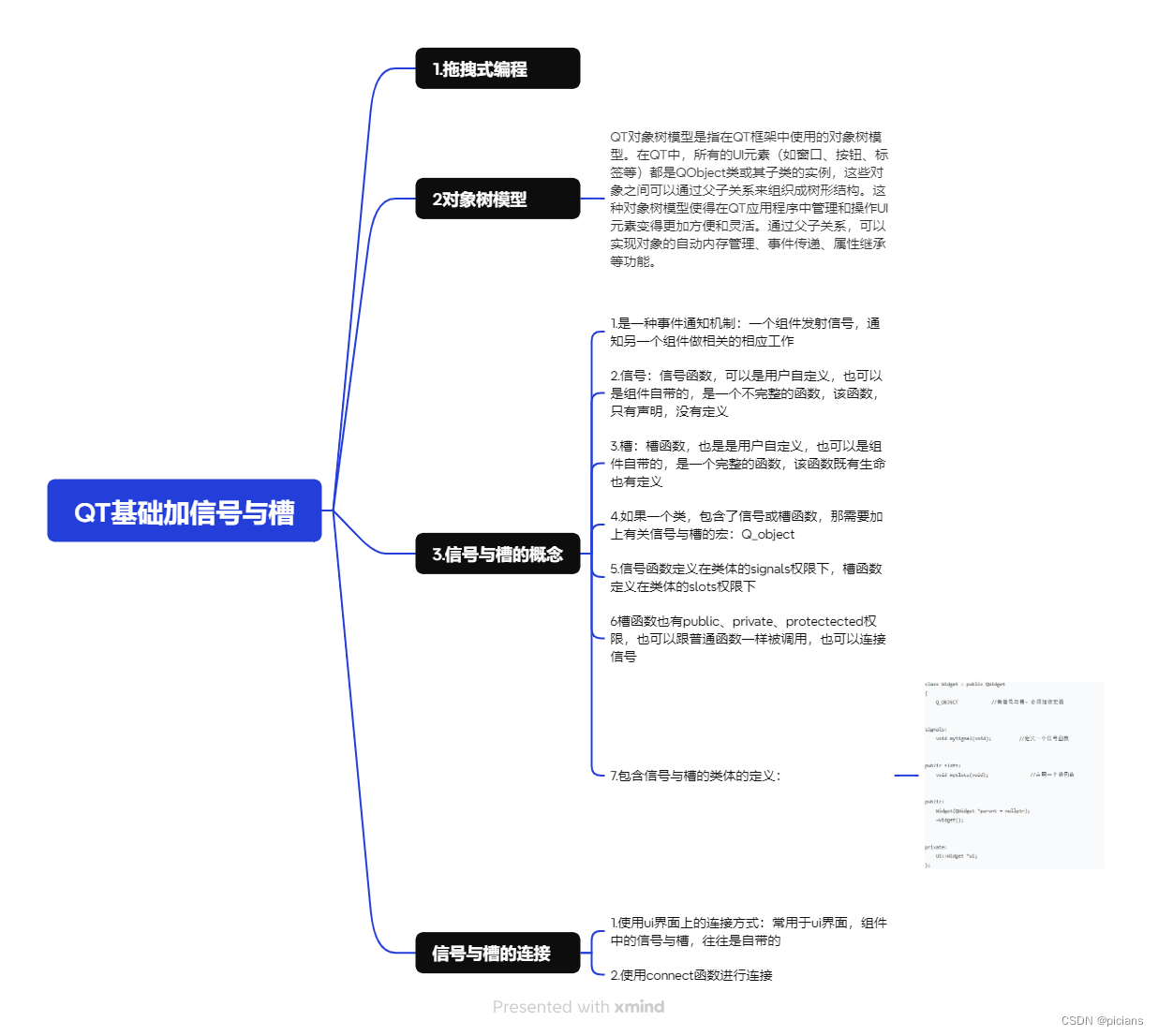
学QT的第二天~
小黑子鉴别界面 #include "mywidget.h" void MyWidget::bth1() { if(edit3 ->text()"520cxk"&&edit4 ->text()"1314520") { qDebug()<< "你好,真爱粉"; this->close(); } else { speecher->sa…...
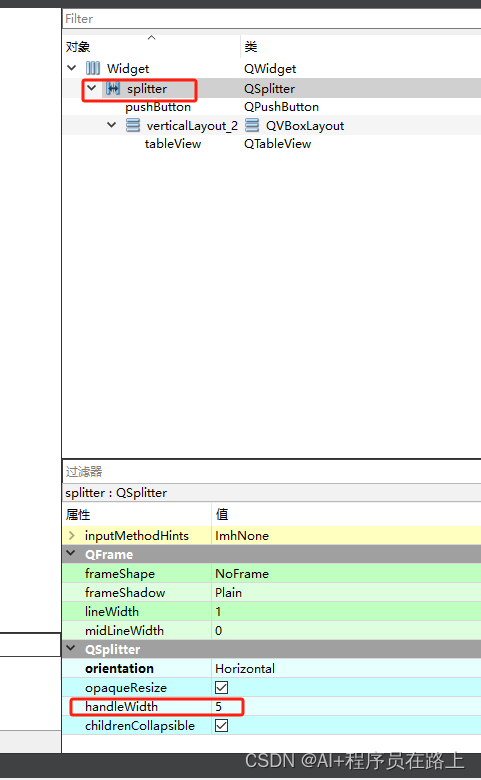
QSplitter分裂器的使用方法
1.QSplitter介绍 QSplitter是Qt框架提供的一个基础窗口控件类,主要用于分割窗口,使用户能够通过拖动分隔条来调节子窗口的大小。 2.QSplitter的添加方法 (1)通过Qt Creator的界面设计工具添加; (2…...

AI-数学-高中52-离散型随机变量概念及其分布列、两点分布
原作者视频:【随机变量】【一数辞典】2离散型随机变量及其分布列_哔哩哔哩_bilibili 离散型随机变量分布列:X表示离散型随机变量可能在取值,P:对应分布在概率,P括号里X1表示事件的名称。 示例:...

Amazon IoT 服务的组件
我们要讨论的第一个组件是设备 SDK。 您的连接设备需要进行编码,以便它们可以与平台连接并执行操作。 Amazon Device SDK 是一个软件开发套件,其中包括一组用于连接、身份验证和交换消息的客户端库。 SDK 提供多种流行语言版本,例如 C、Node.…...
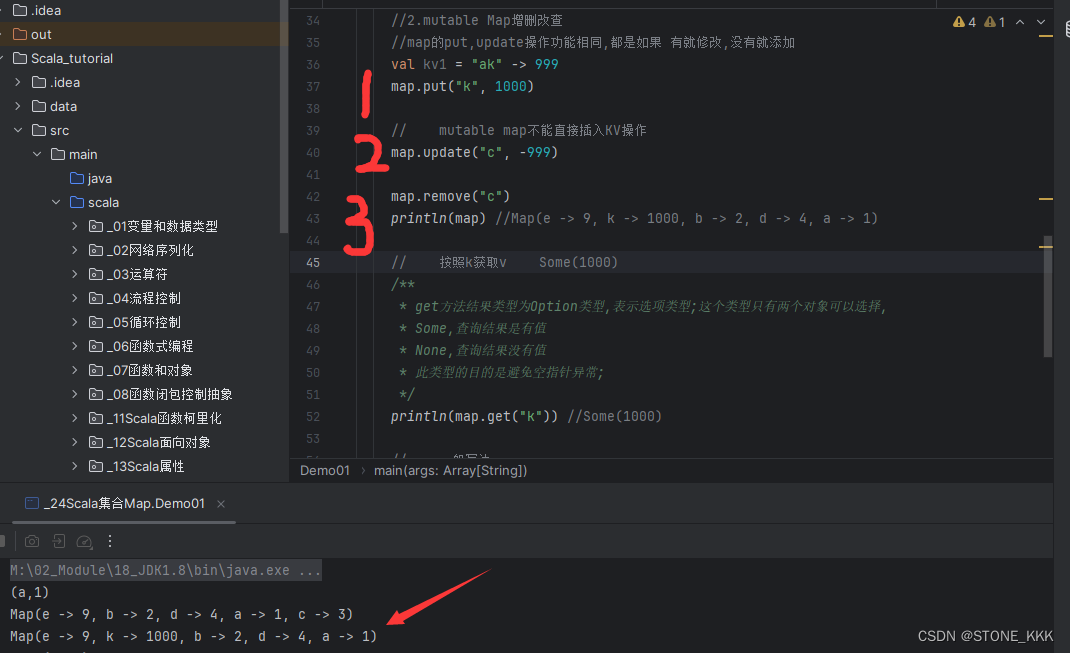
24_Scala集合Map
文章目录 Scala集合Map1.构建Map2.增删改查3.Map的get操作细节 Scala集合Map –默认immutable –概念和Java一致 1.构建Map –创建kv键值对 && kv键值对的表达 –创建immutable map –创建mutable map //1.1 构建一个kv键值对 val kv "a" -> 1 print…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...
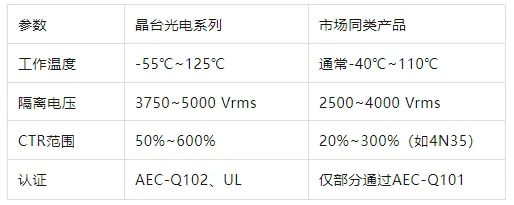
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...
