【Python】numpy.ptp()
numpy.ptp() 函数是 NumPy 库中的一个有用函数,用于计算数组中的“峰到峰”(peak-to-peak)值,即数组中的最大值与最小值之差。这个函数可以帮助快速评估数组中数据的变化范围,常用于信号处理、数据分析等领域中,以确定数据的波动幅度。
基本用法
numpy.ptp() 的基本语法如下:
numpy.ptp(a, axis=None, out=None, keepdims=np._NoValue)
参数解释
- a:输入数组。
- axis:指定计算峰到峰值的轴。默认为
None,在这种情况下,函数计算整个数组的峰到峰值。如果指定了轴,则沿该轴计算每个切片的峰到峰值。 - out:一个用于放置结果的数组。这必须与预期输出的形状和类型匹配。
- keepdims:如果设置为
True,则保持输出的维度与输入相同,即在进行运算的轴上输出的维度为1,否则这些轴将被压缩。
示例
下面是一些使用 numpy.ptp() 的示例,展示如何在实践中应用这个函数:
计算一维数组的峰到峰值
import numpy as np# 创建一个一维数组
arr = np.array([4, 8, 1, 10, 3, 9])
ptp_value = np.ptp(arr)
print("Peak-to-peak value:", ptp_value)
计算多维数组的峰到峰值
# 创建一个二维数组
arr_2d = np.array([[4, 2, 1], [10, 8, 9], [1, 3, 2]])# 计算整个数组的峰到峰值
ptp_value_all = np.ptp(arr_2d)
print("Peak-to-peak value across all elements:", ptp_value_all)# 计算每列的峰到峰值
ptp_value_cols = np.ptp(arr_2d, axis=0)
print("Peak-to-peak value across columns:", ptp_value_cols)# 计算每行的峰到峰值
ptp_value_rows = np.ptp(arr_2d, axis=1)
print("Peak-to-peak value across rows:", ptp_value_rows)
应用场景
- 数据分析:用于估计数据集中的极值差异,帮助了解数据可能的波动范围。
- 信号处理:测量信号的最大波动幅度,对于音频、图像和其他类型的信号处理非常有用。
- 科学计算:在处理实验数据时,估计测量结果的波动范围。
通过了解 numpy.ptp() 的使用,你可以方便地进行各种数据分析和处理任务,特别是那些涉及到需要快速找出数据极差的场景。
相关文章:
)
【Python】numpy.ptp()
numpy.ptp() 函数是 NumPy 库中的一个有用函数,用于计算数组中的“峰到峰”(peak-to-peak)值,即数组中的最大值与最小值之差。这个函数可以帮助快速评估数组中数据的变化范围,常用于信号处理、数据分析等领域中&#x…...

The provided password or token is incorrect or your account
IDEA使用git技巧 【/n】 01 问题出现场景 我的gitlab上个月生成的token到期了,于是今天推上去的时候报了这个错误 The provided password or token is incorrect or your account has 2FA enabled and you must use a personal access token instead of a password. See ht…...

常见的shell命令
以下是一些常见的shell命令: cd:改变当前目录;ls:列出目录中的文件和子目录;mkdir:创建一个新的目录;touch:创建一个新的空文件或更新已存在的文件的时间戳;rmÿ…...

堆栈打印跟踪Activity的启动过程(基于Android10.0.0-r41),framework修改,去除第三方app的倒计时页面
文章目录 堆栈打印跟踪Activity的启动过程(基于Android10.0.0-r41),framework修改,去除第三方app的倒计时页面1.打印异常堆栈2.去除第三方app的倒计时页面3.模拟点击事件跳过首页进入主页 堆栈打印跟踪Activity的启动过程(基于Android10.0.0-r41)&#x…...

只允许内网访问时,如何设置hosts
1、Hosts文件简介 hosts文件是一个没有扩展名的计算机文件,用于将主机名与对应的 IP 地址关联起来。在操作系统中,hosts文件通常用于在本地解析域名,以便将域名映射到特定的IP地址。这个文件可以用来屏蔽广告、加速访问特定网站、解决DNS解析…...
nature《自然》期刊文献怎么在家查看下载
nature《自然》期刊我们都知道,是世界上历史悠久的、最有名望的科学杂志之一。下载该期刊文献是需要使用权限的,如果你没有nature《自然》期刊的资源,又该如何获取呢?请看本文的经验分享。 一、先百度“文献党下载器” 在文献党下…...

python作业五
题目:注册登录 制作一个注册登录模块 注册:将用户填入的账户和密码保存到一个文件(users.bin) 登陆:将用户填入账户密码和users.bin中保存的账户密码进行比对,如果账户和密码完全相同 那 么登录成功,否则登录失败…...

经典的设计模式和Python示例(一)
目录 一、工厂模式(Factory Pattern) 二、单例模式(Singleton Pattern) 三、观察者模式(Observer Pattern) 一、工厂模式(Factory Pattern) 工厂模式(Factory Pattern…...

Ubuntu服务器如何安装桌面
更新软件库 apt-get update 升级软件 apt-get upgrade 安装ubuntu桌面系统 apt-get install ubuntu-desktop 运行过程需要手动确认两次,选择 Y。 安装完成之后,终端输入 reboot,重启服务器。...
填报表如何实现电话号码的校验
单元格校验时,只能输入数字和特定字符(-),即实现固话和手机号码的校验,保证录入的规范,应如何实现? 解决方案:使用正则表达式实现校验效果,如下图所示: 校验…...
揭秘全网热门话题:抖音快速涨粉方法,巨量千川投流助你日增10000粉
在当今社交媒体的时代( 千川投流:hzzxar)抖音成为了年轻人分享自己才华和生活的平台。然而,要在抖音上快速获得关注和粉丝,却不是一件容易的事情。今天,我们将揭秘全网都在搜索的抖音快速涨1000粉的秘籍,带…...

电脑提示‘找不到msvcr110dll,无法继续执行代码’的解决方法,3分钟快速修复
不知道大家有没有遇到过这种情况,无端端电脑提示你找不到msvcr110dll,无法继续执行代码?当出现这个情况,证明你的某个程序就已经运行不了,你需要去修复这个错误,才能正常的运行程序,下面我们一起来详细的了…...
如何在Hostease的Linux虚拟主机上永久移除WordPress网站
最近有遇到客户咨询如何移除Linux虚拟主机上的WordPress网站的, 因为原先的站点长时间不更新,被恶意篡改,跳转到了一个博彩网站上,本身网站也比较旧了,客户也不准备修复,准备重新建站。但是又怕移除不干净&…...

【云原生】Docker 的网络通信
Docker 的网络通信 1.Docker 容器网络通信的基本原理1.1 查看 Docker 容器网络1.2 宿主机与 Docker 容器建立网络通信的过程 2.使用命令查看 Docker 的网络配置信息3.Docker 的 4 种网络通信模式3.1 bridge 模式3.2 host 模式3.3 container 模式3.4 none 模式 4.容器间的通信4.…...

如何优雅的实现浏览器多标签通讯
前言 开发过程中无法避免遇到需要进行多标签通讯的情况,例如: 管理员登陆后,其他打开标签的页面登陆状态要变更课堂页面只能打开一个,另一个则通知失效等等。。。场景 然而实现该功能,我们需要使用页面能共同持有的…...
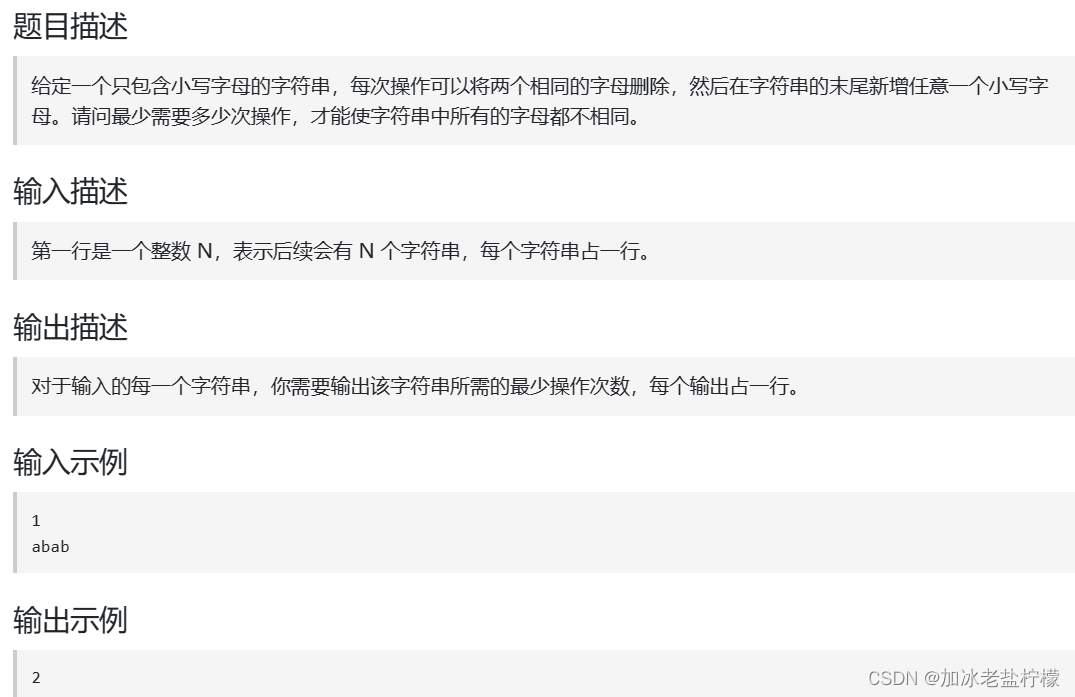
刷题之不相同的字符串(卡码网模拟)
卡码网不同的字符串 #include<vector> #include<string> #include<iostream> using namespace std; int main() {int n0;cin>>n;for(int i0;i<n;i){string s;cin>>s;vector<int>hash(26,0);for(int j 0;j < s.size();j)hash[s[j…...
JS-导入导出
export和export default是ES6中导出模块中变量的语法 导入导出变量 //导出方法(js文件中) export const 变量名值//导入方法 对应导入的变量,一定要加花括号 import {变量名} from js文件路径 导入导出函数 //导出方法(js文件中…...

【代码随想录——数组篇】
代码随想录——数组篇 2. 二分查找3. 移除元素4. 有序数组的平方5. 长度最小的子数组6. 螺旋矩阵II 2. 二分查找 力扣题目链接 前提: 有序数组数组中无重复元素 代码: (版本一)左闭右闭区间 class Solution {public int sea…...

使用 js 类封装项目中音频播放功能的工具方法utils
在前端开发中,音频播放功能是一个常见的需求,我们经常需要在项目中加入音频播放、音频提示等功能。为了提高开发效率和代码复用性,我们可以封装一个工具方法来管理音频播放功能。 在本文中,我将介绍如何封装项目中音频播放功能的…...

【超详细】R语言贝叶斯方法在生态环境领域中的高阶技术应用
查看原文>>>R语言贝叶斯方法在生态环境领域中的高阶技术应用 目录 专题一:前期资料 专题二:R和Rstudio入门和绘图(含ggplot) 专题三:R语言数据清洗-tidyverse包应用 专题四:贝叶斯回归模型-回…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

篇章一 论坛系统——前置知识
目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...
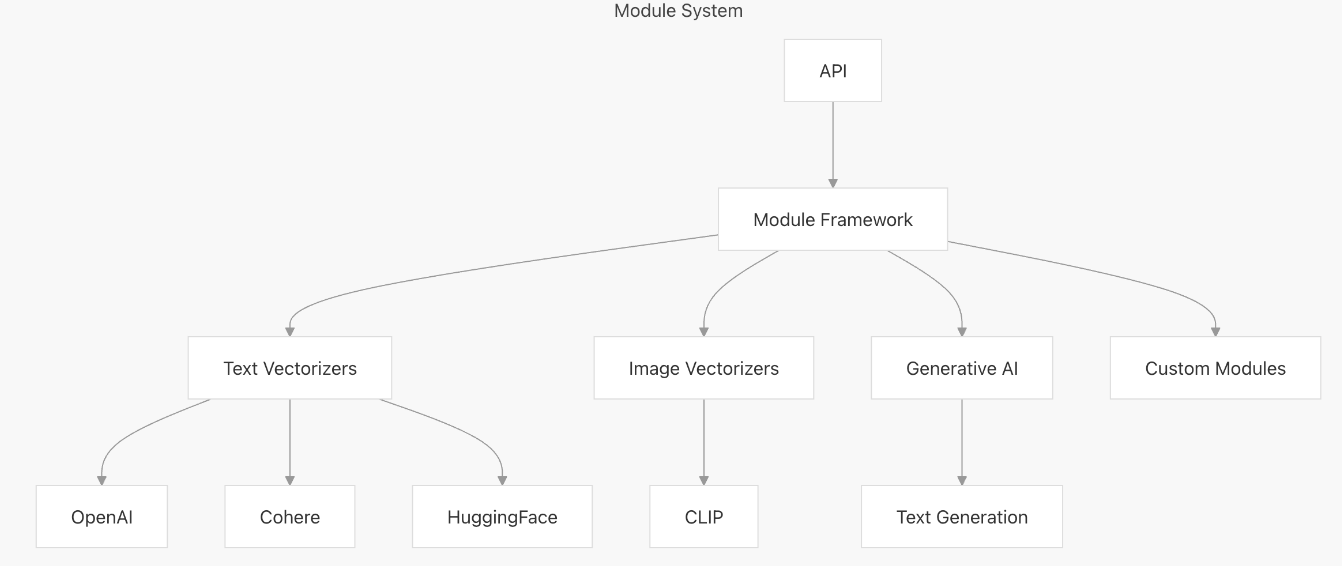
【向量库】Weaviate概述与架构解析
文章目录 一、什么是weaviate二、High-Level Architecture1. Core Components2. Storage Layer3. 组件交互流程 三、核心组件1. API Layer2. Schema Management3. Vector Indexing3.1. 查询原理3.2. 左侧:Search Process(搜索流程)3.3. 右侧&…...
