当前位置： 首页 > news >正文

MAVEN打包JAR启动执行manifest

news 2026/2/10 3:39:40

当您使用Maven进行项目打包，特别是需要创建一个可执行的JAR文件时，确保JAR文件的MANIFEST.MF中包含正确的Main-Class属性是非常重要的。这个属性告诉Java运行时环境哪个类包含main方法，作为应用程序的入口点。

如果您发现生成的JAR文件不包含Main-Class属性，您可以在maven-assembly-plugin插件的配置中指定它。以下是如何在Maven的pom.xml文件中配置maven-assembly-plugin以包含Main-Class属性的示例：

<plugin><artifactId>maven-assembly-plugin </artifactId><configuration><descriptorRefs><!-- 此处填写打包后jar包后添加的标识 --><descriptorRef>jar-with-dependencies</descriptorRef></descriptorRefs><archive><manifest><!-- 此处填写程序的主入口(main方法) --><mainClass>com.example.demo.Main</mainClass></manifest></archive></configuration><executions><execution><id>make-assembly</id><phase>package</phase><goals><goal>single</goal></goals></execution></executions>
</plugin>

相关文章：

MAVEN打包JAR启动执行manifest

当您使用Maven进行项目打包&#xff0c;特别是需要创建一个可执行的JAR文件时&#xff0c;确保JAR文件的MANIFEST.MF中包含正确的Main-Class属性是非常重要的。这个属性告诉Java运行时环境哪个类包含main方法&#xff0c;作为应用程序的入口点。 如果您发现生成的JAR文件不包含…...

编程日记 2024/5/9 7:59:09

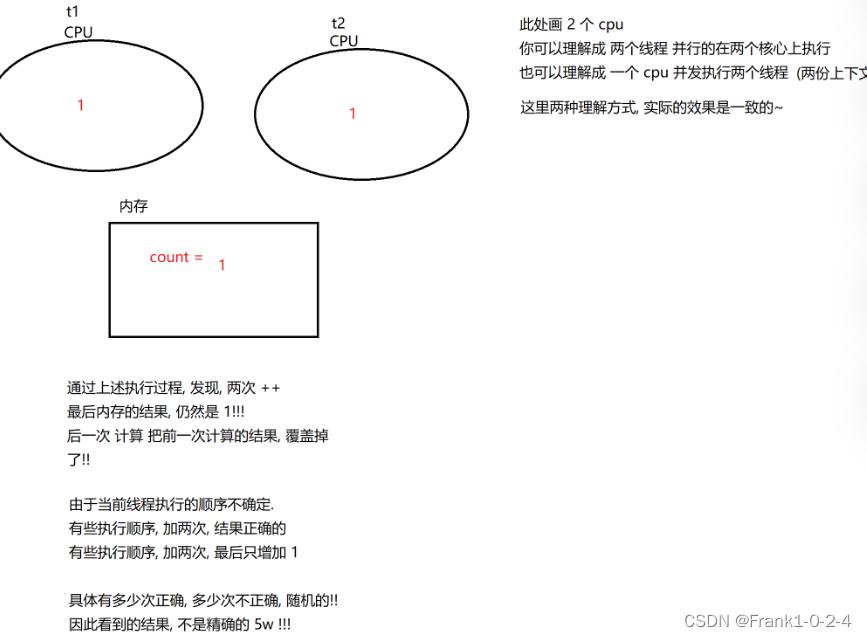
JavaEE 多线程详细讲解（1）

1.线程是什么 &#xff08;shift F6&#xff09;改类名 1.1.并发编程是什么 &#xff08;1&#xff09;当前的CPU&#xff0c;都是多核心CPU &#xff08;2&#xff09;需要一些特定的编程技巧&#xff0c;把要完成的仍无&#xff0c;拆解成多个部分&#xff0c;并且分别让…...

编程日记 2024/5/9 7:54:04

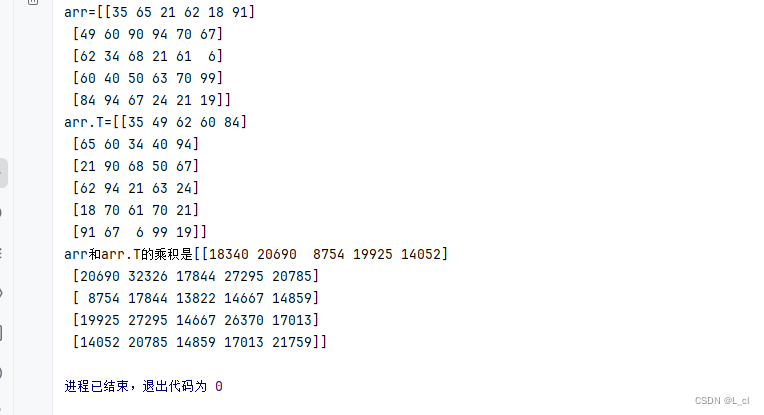
数据分析从入门到精通 1.numpy剑客修炼

会在某一瞬间突然明白&#xff0c;有些牢笼是自己给自己的 —— 24.5.5 一、数据分析秘笈介绍 1.什么是数据分析 是把隐藏在一些看似杂乱无章的数据背后的信息提炼出来&#xff0c;总结出所研究对象的内在规律。使得数据的价值最大化 案例&#xff1a; 分析用户的消…...

编程日记 2024/5/9 7:53:02

【iOS】KVO

文章目录 前言一、KVO使用1.基本使用2.context使用3.移除KVO通知的必要性4.KVO观察可变数组 二、代码调试探索1.KVO对属性观察2.中间类3.中间类的方法3.dealloc中移除观察者后&#xff0c;isa指向是谁&#xff0c;以及中间类是否会销毁&#xff1f;总结 三、KVO本质GNUStep窥探…...

编程日记 2024/5/9 7:52:01

python json字符串怎么用format方法填充参数值报KeyError

python json字符串怎么用format方法填充参数值报KeyError 需求问题分析解决方案 需求 因为python中的字典和json中的一些变量有差异&#xff0c;比如&#xff1a;json中有null、true&#xff0c;在python中就不会被识别&#xff0c;只能转换成字符串&#xff0c;在通过loads()…...

编程日记 2024/5/9 7:48:57

C++新手村指南：入门基础

目录 C概念 C发展史 C关键字&#xff08;C98&#xff09; 命名空间 命名空间的定义 命名空间的使用 C中的输入&&输出 缺省参数 缺省参数的概念 缺省参数的分类 函数重载 函数重载概念 函数重载实现 引用 引用的概念 引用的特性 常引用 引用的使用场景…...

编程日记 2024/5/9 7:47:56

智慧旅游推动旅游服务智慧化转型：借助智能科技的力量，实现旅游资源的精准匹配和高效利用，为游客提供更加便捷、舒适的旅游环境

目录 一、引言 二、智慧旅游的定义与特点 &#xff08;一&#xff09;智慧旅游的定义 &#xff08;二&#xff09;智慧旅游的特点 三、智能科技在旅游服务中的应用 &#xff08;一&#xff09;大数据分析助力旅游决策 &#xff08;二&#xff09;人工智能实现个性化推荐…...

编程日记 2024/5/9 7:45:54

Hikyuu-PF-银行股轮动交易策略实现

今天&#xff0c;带来的是“如何使用 Hikyuu 中的投资组合来实现银行股轮动交易策略”。 这个策略的逻辑很简单&#xff1a;持续持有两支市净率最低银行股&#xff0c;然后每月换仓 定义回测周期与回测标的 同样&#xff0c;首先定义回测周期&#xff1a; # 定义回测日期 …...

编程日记 2024/5/9 7:44:53

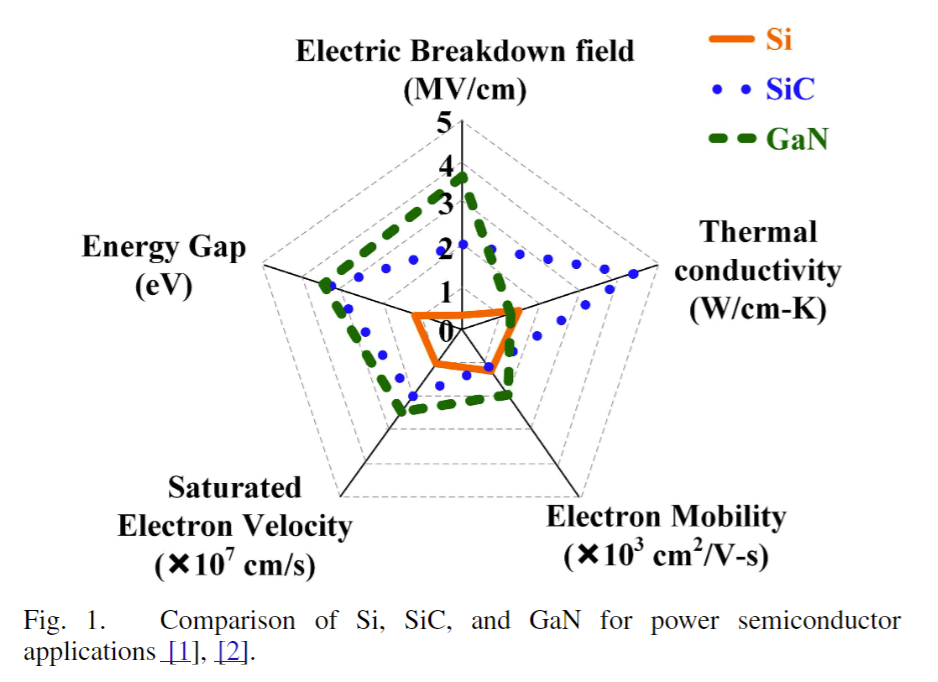
【氮化镓】GaN功率器件在转换器设计中的挑战

I. 引言（INTRODUCTION） 宽带隙（WBG）器件的重要性： 引言部分首先强调了宽带隙（WBG）器件在高频、高效率电力电子技术中的关键作用。这些器件，包括碳化硅（SiC）和氮化镓（GaN），相较于传统的硅功率器件，具有显著的优势。宽带隙半导体材料的高击穿场强允许设计更薄的漂…...

编程日记 2024/5/9 7:43:51

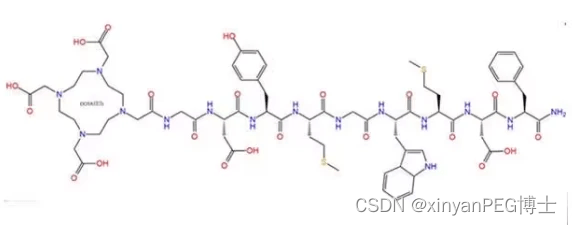
DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2，1306310-00-8，是一种重要的多肽化合物

一、试剂信息 名称&#xff1a;DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2CAS号&#xff1a;1306310-00-8结构式&#xff1a; 二、试剂内容 DOTA-Gly-Asp-Tyr-Met-Gly-Trp-Met-Asp-Phe-NH2是一种重要的多肽化合物&#xff0c;其CAS号为1306310-00-8。该多肽包含一个DO…...

编程日记 2024/5/9 7:41:49

CopyClip for Mac - 高效复制粘贴，轻松管理剪贴板

CopyClip for Mac&#xff0c;一款专为Mac用户打造的剪贴板管理工具&#xff0c;让你在复制粘贴的日常任务中&#xff0c;享受到前所未有的高效与便捷。 它常驻在菜单栏中&#xff0c;时刻准备为你服务。一旦你复制了内容&#xff0c;CopyClip就会自动将其保存至历史记录中&…...

编程日记 2024/5/9 7:39:47

[windows系统安装/重装系统][step-1]U盘启动盘制作，微软官方纯净系统镜像下载

前言 U盘至少8GB吧我这刚好有个空闲的U盘8GB容量&#xff0c;制作启动盘且放入一个最新win10官方镜像足够 不是天天装系统&#xff0c;至少USB2.0 (我用的2.0的一个闲置U盘)即可&#xff0c;当然平时传资料什么的3.0会快些 U盘启动盘仅需要制作一次&#xff0c; U盘启动盘制…...

编程日记 2024/5/9 7:37:44

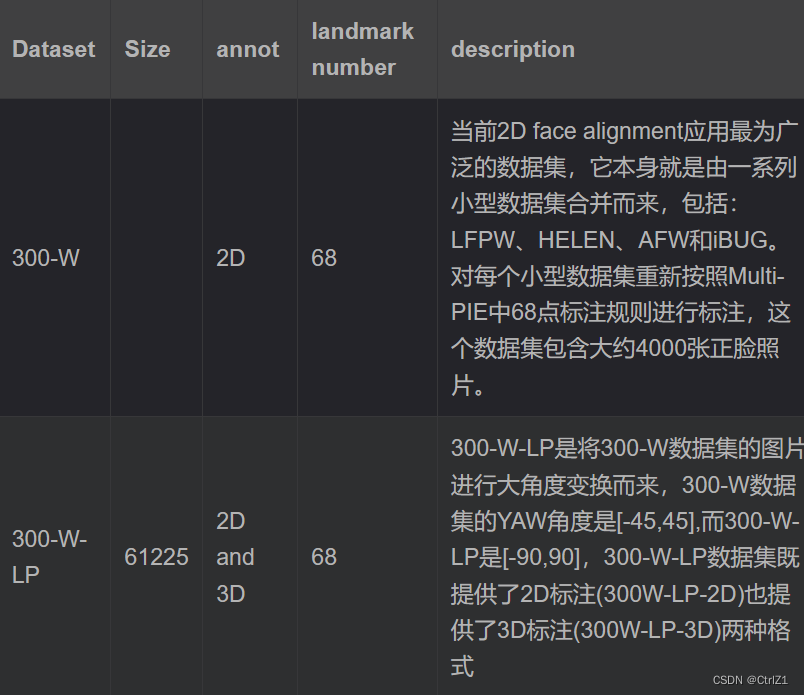
AI换脸原理(4)——人脸对齐（关键点检测）参考文献2DFAN：代码解析

注意，本文属于人脸关键点检测步骤的论文，虽然也在人脸对齐的范畴下。 1、介绍 在本文中，重点介绍了以下几项创新性的成果，旨在为人脸关键点检测领域带来新的突破。 首先，成功构建了一个卓越的2D人脸关键点检测基线模型。这一模型不仅集成了目前最优的关键点检测网络结构，…...

编程日记 2024/5/9 7:35:42

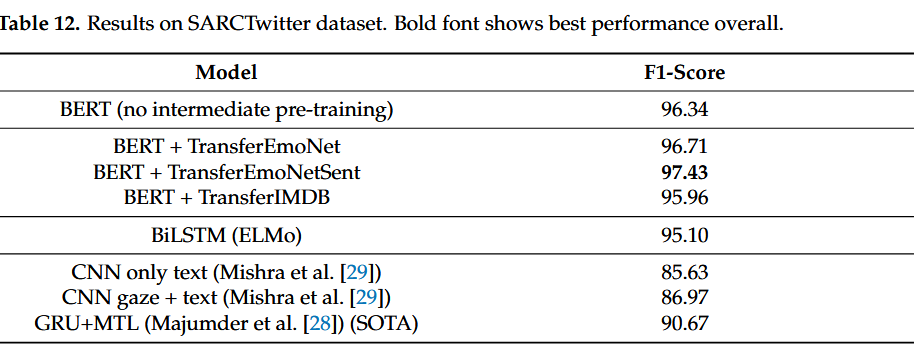
Sarcasm detection论文解析 |使用 BERT 进行中间任务迁移学习的刺检测

论文地址 论文地址&#xff1a;https://www.mdpi.com/2227-7390/10/5/844#/ github&#xff1a;edosavini/TransferBertSarcasm (github.com) 论文首页 笔记框架 使用 BERT 进行中间任务迁移学习的讽刺检测 &#x1f4c5;出版年份:2022 &#x1f4d6;出版期刊:Mathematics &…...

编程日记 2024/5/9 7:32:39

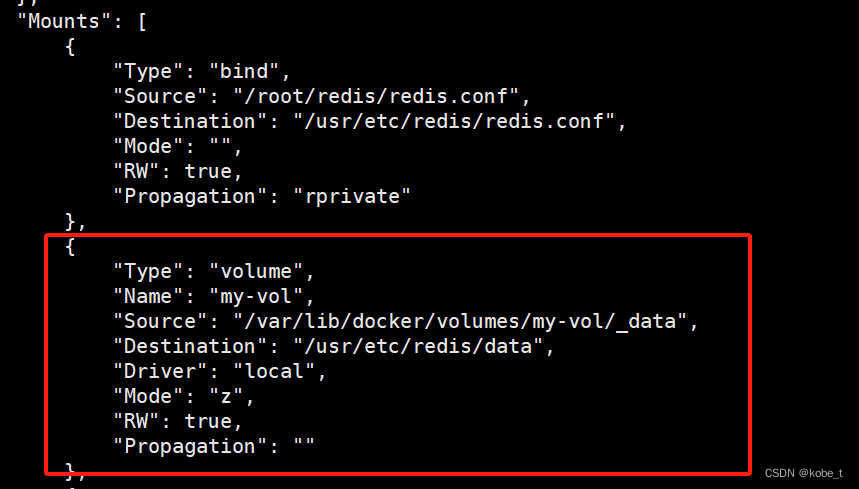
docker系列9：容器卷挂载(下)

传送门 docker系列1&#xff1a;docker安装 docker系列2&#xff1a;阿里云镜像加速器 docker系列3&#xff1a;docker镜像基本命令 docker系列4&#xff1a;docker容器基本命令 docker系列5&#xff1a;docker安装nginx docker系列6&#xff1a;docker安装redis docker系…...

编程日记 2024/5/9 7:31:37

QT ERROR: Unknown module(s) in QT: xlsx怎么办

现象描述 QT编译c代码的时候&#xff0c;报这种QT ERROR: Unknown module(s) in QT: xlsx&#xff0c;应该如何解决&#xff1f; 这里&#xff0c;我简单记录一下自己的解决问题过程。有可能&#xff0c;对遇到同样的问题的你&#xff0c;也有所帮助 第一步 检查perl是否安装…...

编程日记 2024/5/9 7:29:36

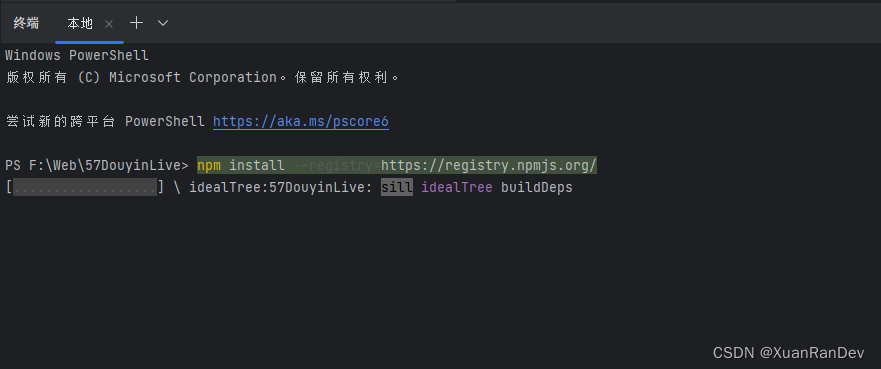
npm install 卡在reify:rxjs: timing reifyNode的解决办法

今天要逆向跑一个electron&#xff0c;但是npm install一直卡在 reify:element-plus: timing reifyNode:node_modules/lodash Completed in 6664ms这里一动不动&#xff0c;一番研究之后发现可能跟用的镜像有关系&#xff0c;我原本是官方镜像&#xff0c;总感觉第三方镜像有一…...

编程日记 2024/5/9 7:28:34

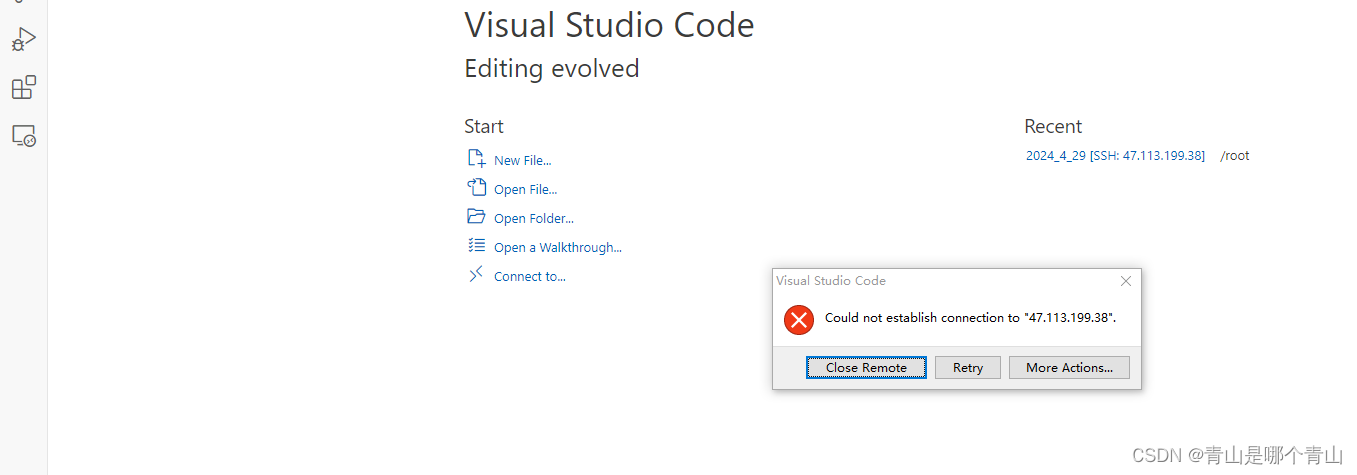
VScode 无法连接云服务器

试了很多方法&#xff0c;比如更换VScode版本&#xff0c;卸载重装&#xff0c;删除配置文件 重启电脑&#xff0c;都无法成功。最后重置电脑后才连接上&#xff0c;但是重启服务器后又出现该问题。 方法一&#xff1a;修改环境 方法二&#xff1a;把vscode卸载干净重下...

编程日记 2024/5/9 7:27:33

Kafka 面试题（二）

1. 简述Kafka 的工作流程 &#xff1f; Kafka的工作流程涉及多个关键组件和步骤&#xff0c;确保了消息的可靠传输和处理。以下是Kafka工作流程的简要概述&#xff1a; 生产者发布消息&#xff1a;生产者&#xff08;Producer&#xff09;是Kafka工作流程的起点&#xff0c;它…...

编程日记 2024/5/9 7:25:31

Spring Cloud Kubernetes 本地开发环境调试

一、Spring Cloud Kubernetes 本地开发环境调试 上面文章使用 Spring Cloud Kubernetes 在 k8s 环境中实现了服务注册发现、服务动态配置&#xff0c;但是需要放在 k8s 环境中才能正常使用&#xff0c;在本地开发环境中可能没有 k8s 环境&#xff0c;如何本地开发调试呢&#…...

编程日记 2024/5/9 7:24:30

rknn优化教程（二）

文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK&#xff0c;开始写第二篇的内容了。这篇博客主要能写一下&#xff1a; 如何给一些三方库按照xmake方式进行封装&#xff0c;供调用如何按…...

编程新知 2025/6/11 15:25:30

Oracle查询表空间大小

1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

编程新知 2025/11/8 0:24:13

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2026/2/2 22:06:13

《基于Apache Flink的流处理》笔记

思维导图 1-3 章 4-7章 8-11 章 参考资料 源码&#xff1a; https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

编程新知 2026/1/31 14:55:53

成都鼎讯硬核科技！雷达目标与干扰模拟器，以卓越性能制胜电磁频谱战

在现代战争中&#xff0c;电磁频谱已成为继陆、海、空、天之后的 “第五维战场”&#xff0c;雷达作为电磁频谱领域的关键装备&#xff0c;其干扰与抗干扰能力的较量&#xff0c;直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器&#xff0c;凭借数字射…...

编程新知 2026/2/1 7:18:47

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11

C#中的CLR属性、依赖属性与附加属性

CLR属性的主要特征 封装性&#xff1a; 隐藏字段的实现细节 提供对字段的受控访问 访问控制&#xff1a; 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性&#xff1a; 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑&#xff1a; 可以…...

编程新知 2025/12/4 0:13:33

【从零学习JVM|第三篇】类的生命周期(高频面试题)

前言&#xff1a; 在Java编程中&#xff0c;类的生命周期是指类从被加载到内存中开始&#xff0c;到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期&#xff0c;让读者对此有深刻印象。 目录 ​…...

编程新知 2026/1/26 8:42:13

uniapp手机号一键登录保姆级教程（包含前端和后端）

目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号&#xff08;第三种&#xff09;后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

编程新知 2026/1/27 2:03:36

MinIO Docker 部署：仅开放一个端口

MinIO Docker 部署：仅开放一个端口 在实际的服务器部署中，出于安全和管理的考虑，我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务，支持 Docker 部署，但默认情况下它需要两个端口：一个是 API 端口（用于存储和访问数据），另一个是控制台端口（用于管理界面…...

编程新知 2025/12/23 11:08:56