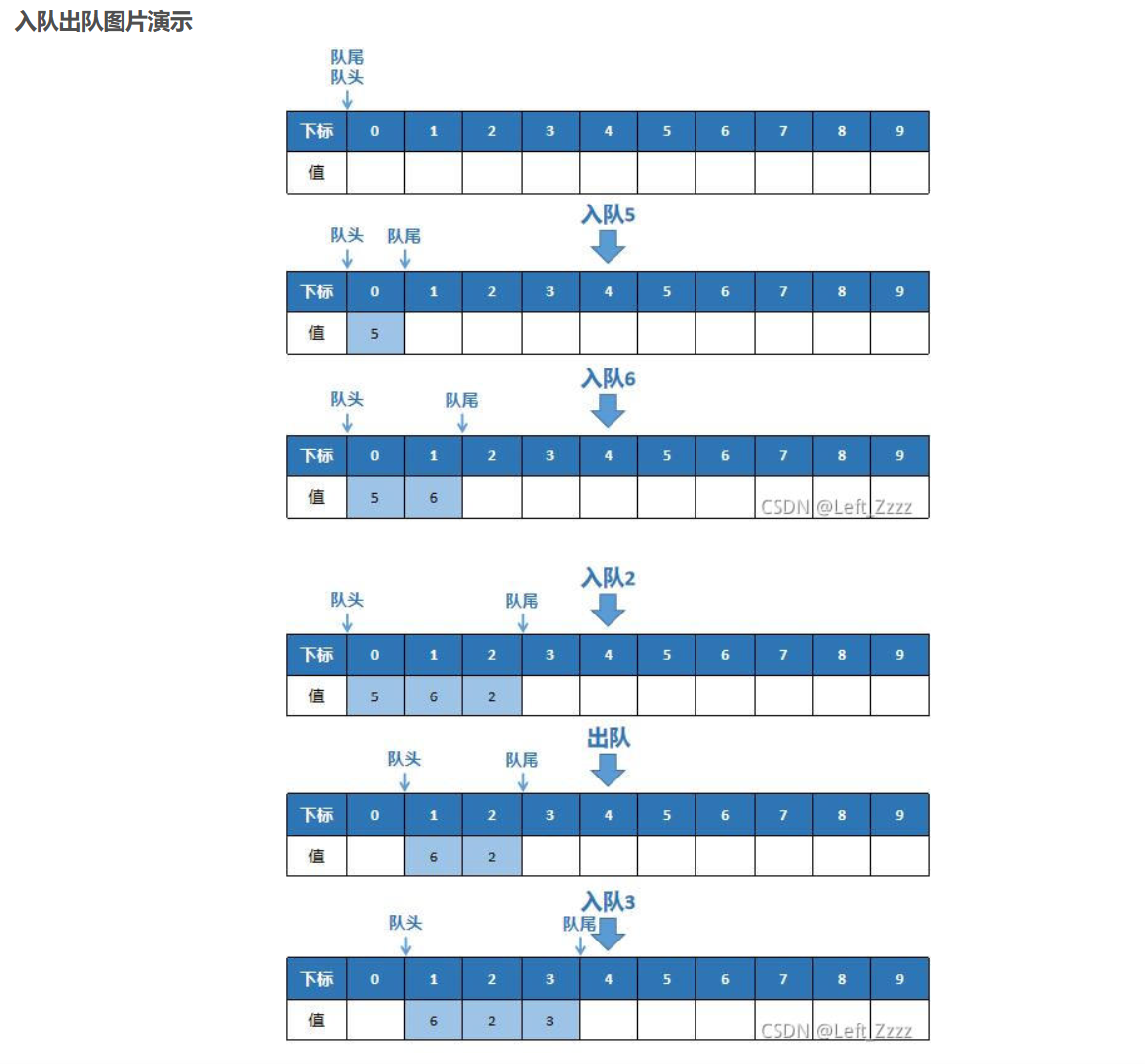
单单单单单の刁队列
在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理一些特定问题时非常有用,比如滑动窗口的单调性问题。
单调队列所解决的问题
单调队列主要是为了求滑动窗口最大/最小值。单调队列是双端队列(首尾两边都可以append和pop)。具体而言,我们会在单调队列的队尾pop和append,会在队首pop
滑动窗口:只能左边界L向右移动或不动、右边界R向右移动或不动,二者不能向左移动。
基本概念
单调队列的类型:
从头到尾递减:可以求滑动窗口内的最大值
从头到尾递增:可以求滑动窗口内的最小值
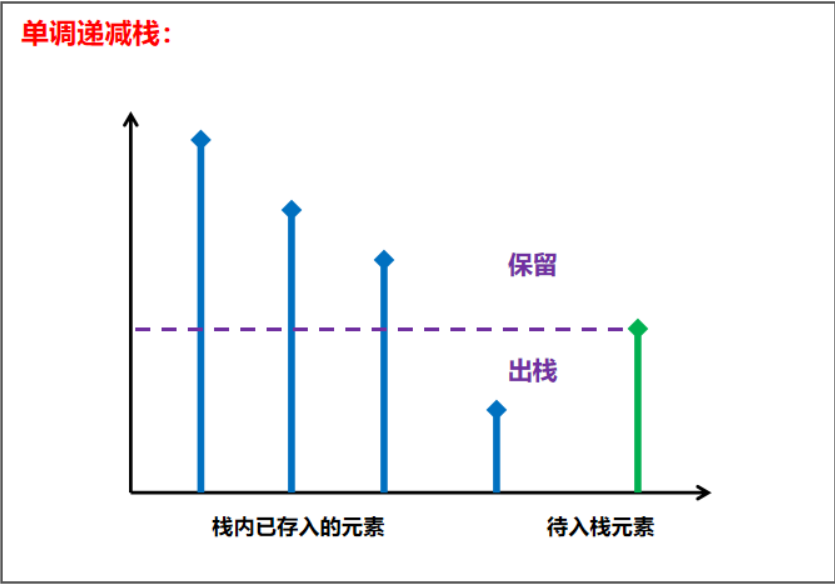
我们之前学过单调栈:

由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己小的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己小的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己大的元素),此时栈顶元素就是数组中左侧第一个比自己小的元素;
由上图可以看出,对于栈内元素来说:
- 在栈内左边的数就是数组中左边第一个比自己大的元素;
- 但元素被弹出时,遇到的就是数组中右边第一个比自己大的元素。
对于将要入栈的元素来说:在对栈进行更新后(即弹出了所有比自己小的元素),此时栈顶元素就是数组中左侧第一个比自己大的元素;
!!!!!!!!!!!!!!单调队列在这里的操作其实是和单调栈差不多的!!!!!!!!!!
为什么要选择这样的单调性:
首先规定队首的元素是我们需要的最值(这一点非常重要),所以递减队列的队首是最大值,递增队列的队首是最小值。其次我们从下面对队列中元素的理解也可以看到。从队首到队尾的元素成为所需最值的优先级需要依次递减。
在单调队列中,头和尾都可以pop,但只有尾可以append。
特别注意:单调队列里存放的是index(下标)而不是元素值(其实也可以是(value, index)这种),这是因为我们无法用元素值来判断元素是否过期。但是我们在谈论元素大小时,指的不是index的大小,而是index在原数组对应value的大小。
用法
以求最大值的单调队列为例,其进出队规则如下:
该单调队列要求其中元素是从头到尾递减。遍历一个数组,所有元素依次入队。
在入队时,若该元素比队尾元素小,直接从队尾入队仍能保持单调性,那么从尾部直接入队即可。
若该元素比队尾元素大,那么要将队尾元素不停pop,直到队尾元素比该元素大(满足单调性),将该元素从队尾入队。
另外注意,当元素过期(已经不在滑动窗口内),将该元素在队首出队。
什么时候生成记录:每当形成一个窗口时就收集答案。
如何获取滑动窗口的最大值:即双端队列头部的值
理解单调队列的进出原因:
队列中的元素表示,如果此时从左往右,那么从队首到队尾的元素表示能够成为滑动窗口最大值的优先级(即哪些元素会依次称为最大值)。优先级高的元素应当值更大、值相同的情况下下标更晚过期(这就处理了具有重复值的情况)。
我们按照这样的理解来审视上面的进出队规则:
如果我们希望从队尾入队的元素比队尾已有的元素大,说明其称为最大值的优先级更高,所以需要pop掉已有的队尾元素。如果希望入队的元素比队尾已有元素小,说明其优先级低,所以可以直接入队。
对于重复值情况的说明:当即将入队的元素和队尾此时的元素重复的时候,新来的元素其下标更晚过期,所以其优先级更高,所以队中的旧元素应当被pop掉。因此队中的元素其实是严格递减的。
如何解决滑动窗口内的最小值问题呢?其实是一样的,不过我们把最小值放在队首,队中元素依次递增。
Java实现单调队列
在Java中,我们可以通过继承LinkedList类来实现一个单调队列。下面是一个简单的单调递增队列的实现示例:
import java.util.LinkedList;public class MonotonicQueue {private LinkedList<Integer> queue;public MonotonicQueue() {queue = new LinkedList<>();}public void offer(int num) {// 维护单调性,移除所有比当前元素大的元素while (!queue.isEmpty() && queue.getLast() < num) {queue.pollLast();}queue.offer(num);}public int peek() {return queue.peekFirst();}public int poll() {return queue.poll();}// 检查队列是否为空public boolean isEmpty() {return queue.isEmpty();}
}
单调队列的c语言(数组版)
int deque[1000];
int h = 0, t = 0;
int pop {if (h < t) {t--;}return deque[t];
}
int isEmpty() { return h == t;
}
void push(int x) { deque[t++] = x;
}
int peek(){return deque[t-1];
}
int poll(){return deque[h++];
}
int main(){
//操作,如while(h<t&&deque[t-1]<nums[i]){t--;}
}
示例:
239. 滑动窗口最大值 - 力扣(LeetCode)

在队列中,索引对应的元素值是递减的,队首元素对应的元素值最大,队尾元素对应的元素值最小。
在这里双端队列来实现单调。队列中存储的是数组中元素的索引。
初始化一个h,t变量用来表示队头队尾
先从数组的第一个元素开始遍历,维护一个递减的双端队列。在这个阶段,由于窗口大小为 k,所以只需要遍历数组的前 k-1 个元素。
如果当前元素大于队尾元素,则将队尾元素出队,直到队列为空或者当前元素小于等于队尾元素。然后将当前元素的索引入队。
在这个时候,虽然队列里的东西不一定是k-1,但是初始化的窗口已经到了k-1.
然后从第 k 个元素开始遍历数组,每次遍历都会对双端队列进行维护,并且将当前窗口的最大值,也就是队头元素(h)记录在结果数组中。
在滑动窗口阶段,从第 k 个元素开始遍历数组。继续维护递减的双端队列,将当前元素入队。然后将当前窗口的最大值记录在结果数组中。
在每次左边窗口加1时,判断队首元素是否已经不在当前窗口内,如果不在,则将队首元素出队。
最后返回答案数组即可
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] deque = new int[nums.length];int h = 0, t = 0;for (int i = 0; i < k - 1; i++) {while (h < t && nums[deque[t - 1]] <= nums[i]) {t--;}deque[t++] = i;}int x = nums.length - k + 1;int[] ans = new int[x];for (int l = 0, r = k - 1; l < nums.length - k + 1; l++, r++) {while (h < t && nums[deque[t - 1]] <= nums[r]) {t--;}deque[t++] = r;ans[l] = nums[deque[h]];if (deque[h] == l) {h++;}}return ans;}
}
// 定义一个指向整数的指针数组,用于存储滑动窗口中元素的索引
int deque[numsSize];// 初始化头部和尾部索引
int h = 0, t = 0;// 填充双端队列的前 k-1 个元素
for (int i = 0; i < k - 1; i++) {// 维护双端队列的单调性:移除所有比当前元素小的元素while (h < t && nums[deque[t - 1]] <= nums[i]) {t--;}// 将当前元素的索引加入到双端队列中deque[t++] = i;
}// 分配内存用于存储滑动窗口最大值的结果
int* ans = (int*)malloc(sizeof(int) * (numsSize - k + 1));// 滑动窗口遍历整个数组
for (int l = 0, r = k - 1; l < numsSize - k + 1; l++, r++) {// 维护双端队列的单调性:移除所有比当前元素小的元素while (h < t && nums[deque[t - 1]] <= nums[r]) {t--;}// 将当前窗口的最后一个元素的索引加入到双端队列中deque[t++] = r;// 当前窗口的最大值是双端队列头部元素对应的值ans[l] = nums[deque[h]];// 如果双端队列头部元素的索引正好是窗口左边界,则移除头部元素if (deque[h] == l) {h++;}
}// 更新返回的最大值数组的大小
*returnSize = numsSize - k + 1;// 返回结果数组
return ans;
862. 和至少为 K 的最短子数组 - 力扣(LeetCode)

class Solution {// 初始化ans为一个较大的数值,以便在遍历过程中找到更小的值int ans = 100001;public int shortestSubarray(int[] nums, int k) {// deque数组用于存储当前考虑的子数组的索引,实现单调队列的功能int[] deque = new int[nums.length + 1];// 初始化双端队列的头和尾索引int h = 0, t = 0;// sum数组用于存储前缀和,sum[i]表示nums从0到i的元素和long[] sum = new long[nums.length + 1];// 初始化前缀和数组的第一个元素为0sum[0] = 0;// 循环遍历数组numsfor (int i = 0; i <= nums.length; i++) {// 如果不是第一个元素,计算当前位置的前缀和if (i != 0)sum[i] = sum[i - 1] + nums[i - 1];// 维护单调队列:移除所有使得sum[i] - sum[deque[h]] >= k的元素// 因为这些元素之前的子数组和已经不可能满足和至少为kwhile (h < t && sum[i] - sum[deque[h]] >= k) {ans = Math.min(ans, i - deque[h++]); // 更新最短子数组长度}// 维护单调队列:移除所有使得sum[i] <= sum[deque[t - 1]]的元素// 因为这些元素对于找到和至少为k的最短子数组没有帮助while (h < t && sum[i] <= sum[deque[t - 1]]) {t--; // 移除队尾元素}// 将当前元素的索引加入到单调队列中deque[t++] = i;}// 如果ans没有被更新,则说明不存在和至少为k的子数组,返回-1return ans > 100000 ? -1 : ans;}
}
结语
单调队列是一种强大的数据结构,它在处理与窗口相关的算法问题时特别有用。通过维护队列的单调性,我们可以有效地减少不必要的计算,提高算法的效率。
希望这篇博客能够帮助您更好地理解单调队列以及如何在Java中实现和应用它。如果您有任何问题或想要了解更多信息,请在评论区告诉我。
相关文章:

单单单单单の刁队列
在数据结构的学习中,队列是一种常用的线性数据结构,它遵循先进先出(FIFO)的原则。而单调队列是队列的一种变体,它在特定条件下保证了队列中的元素具有某种单调性质,例如单调递增或单调递减。单调队列在处理…...
电脑windows系统压缩解压软件-Bandizip
一、软件功能 Bandizip是一款功能强大的压缩和解压缩软件,具有快速拖放、高速压缩、多核心支持以及广泛的文件格式支持等特点。 Bandizip软件的功能主要包括: 1. 支持多种文件格式 Bandizip可以处理多种压缩文件格式,包括ZIP, 7Z, RAR, A…...
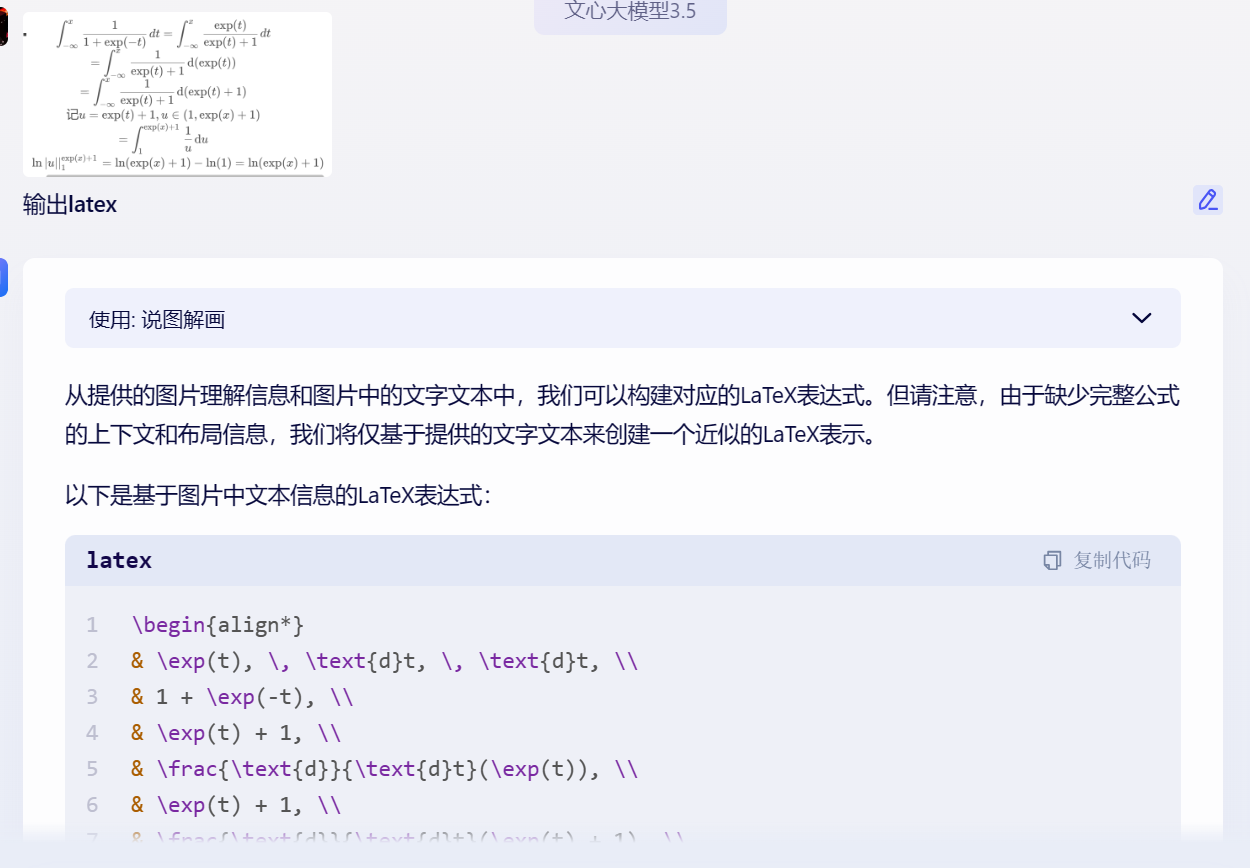
图片公式识别@文档公式识别@表格识别@在线和离线OCR工具
文章目录 abstract普通文字识别本地软件识别公式扩展插件下载小结 在线识别网站/API👺Quicker整合(推荐)可视化编辑和识别公式其他多模态大模型识别图片中的公式排版 开源模型 abstract 本文介绍免费图片文本识别(OCR)工具,包括普通文字识别,公式识别,甚至是手写公…...
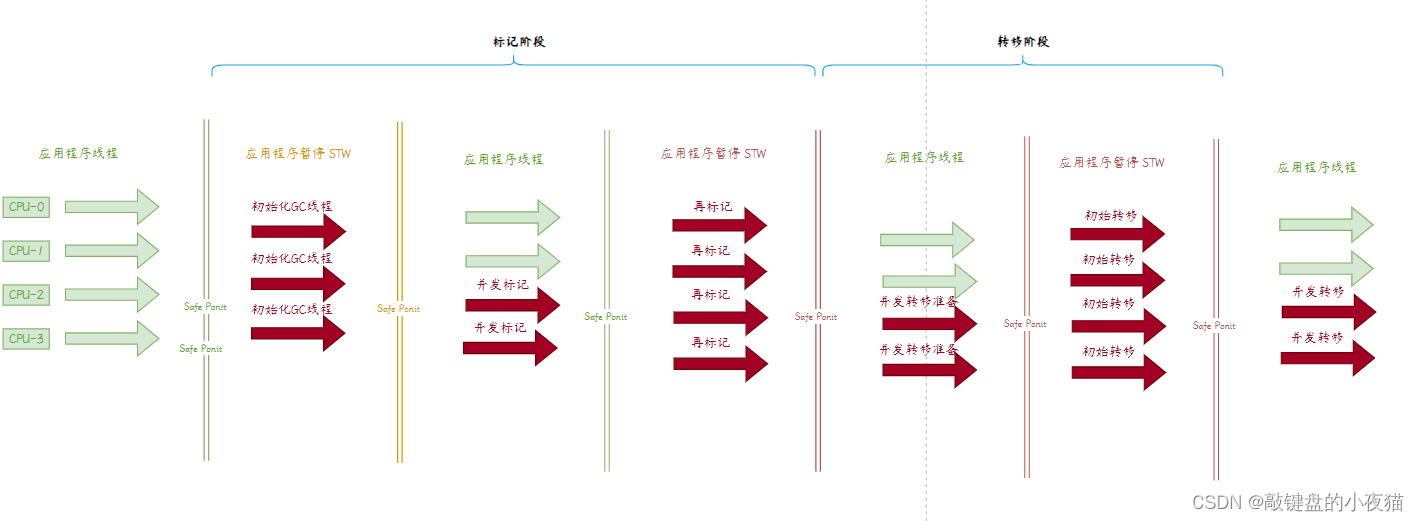
Java高阶私房菜:JVM分代收集算法介绍和各垃圾收集器原理分解
目录 什么是分代收集算法 GC的分类和专业术语 什么是垃圾收集器 垃圾收集器的分类及组合 编辑 应关注的核心指标 Serial和ParNew收集器原理 Serial收集器 ParNew收集器 Parallel和CMS收集器原理 Parallel 收集器 CMS收集器 新一代垃圾收集器G1和ZGC G1垃圾收集器…...

为什么IB损失要在100epochs后再用?
在给定的代码中,参数start_ib_epoch用于控制从第几轮开始使用IB(Instance-Balanced)损失函数进行训练。具体来说,如果start_ib_epoch的值大于等于100,那么在训练的前100轮中将使用普通的交叉熵损失函数(CE&…...
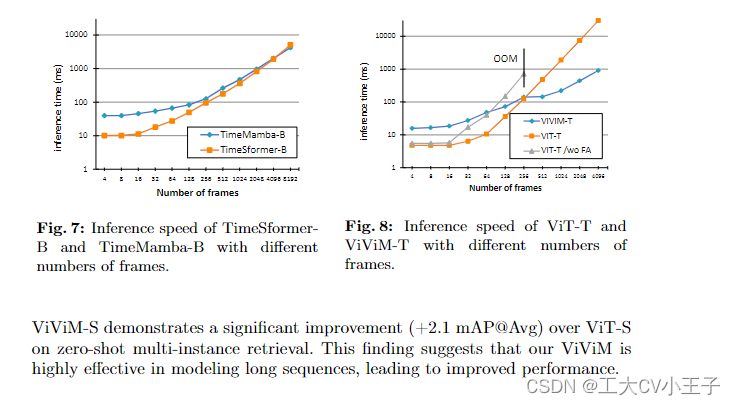
《Video Mamba Suite》论文笔记(4)Mamba在时空建模中的作用
原文翻译 4.4 Mamba for Spatial-Temporal Modeling Tasks and datasets.最后,我们评估了 Mamba 的时空建模能力。与之前的小节类似,我们在 Epic-Kitchens-100 数据集 [13] 上评估模型在zero-shot多实例检索中的性能。 Baseline and competitor.ViViT…...
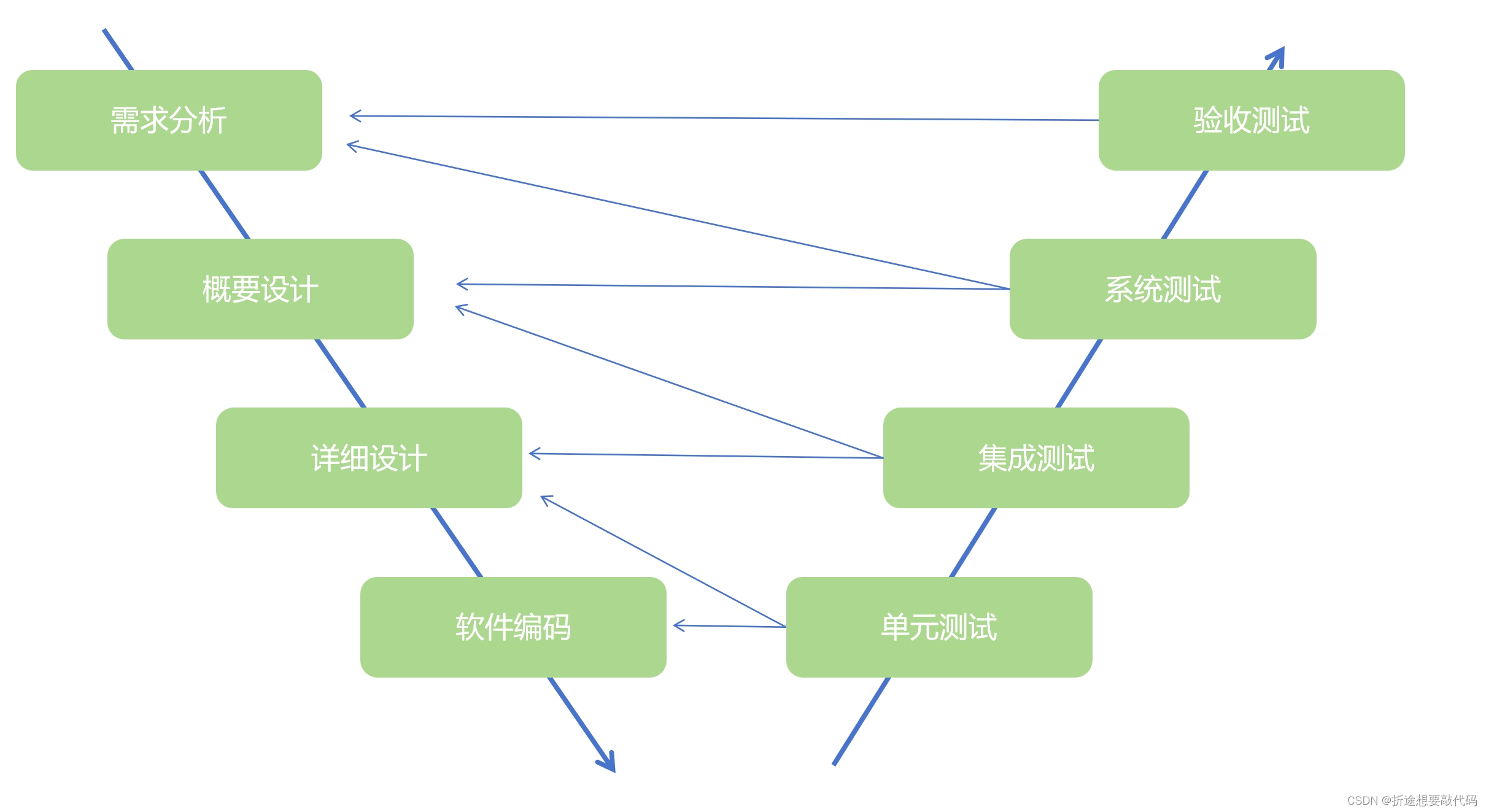
【备战软考(嵌入式系统设计师)】10 - 软件工程基础
这一部分的内容是概念比较多,不要理解,去感受。 涉及的知识点是嵌入式系统开发和维护的部分,也就是和管理相关的,而不是具体如何进行嵌入式系统开发的细节。 系统开发生命周期 按照顺序有下面几个阶段,我们主要要记…...

随手笔记-GNN(朴素图神经网络)
自己看代码随手写的一点备忘录,自己看的,不喜勿喷 GNN (《------ 代码) 刚开始我还在怀疑为什么没有加weigth bias,已经为什么权重才两个,原来是对node_feats进行的network的传播,而且自己内部直接进行了。 下面是一…...

C 语言指针怎么理解?
在今天的学习中,我注意到有位学员似乎对 C 语言指针的理解有些困惑。为了帮助大家更好地理解,我来举个例子。 C 语言指针就好比 Windows 桌面上常见的快捷方式。快捷方式可以指向某个游戏,这就是普通指针;它也可以指向另一个快捷…...

HTTP协议:通信机制、特点及实践应用
目录 前言 1. 运行机制 2. 通信方式 3. 主要特点 4. 统一资源标识符(URL) 5. HTTP报文 6. HTTP请求 7. HTTP响应 8. 实体 9. 持续连接 结语 前言 HTTP(Hypertext Transfer Protocol)是互联网上应用最广泛的一种协议&a…...

Leetcode—289. 生命游戏【中等】
2024每日刷题(126) Leetcode—289. 生命游戏 算法思想 实现代码 class Solution { public:void gameOfLife(vector<vector<int>>& board) {int rows board.size();int cols board[0].size();int neighbors[3] {0, 1, -1};vector<…...
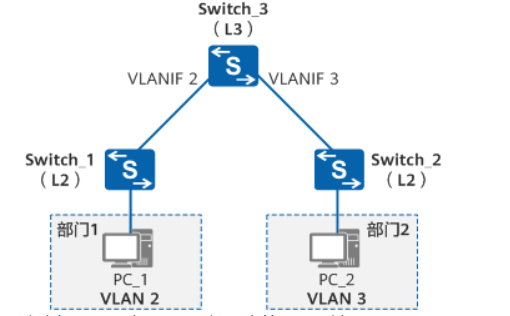
系统运维(虚拟化)
1.VLAN VLAN(Virtual Local Area Network)即虚拟局域网,是将一个物理的LAN在逻辑上划分成多个广播域的通信技术。 每个VLAN是一个广播域,VLAN内的主机间可以直接通信,而VLAN间则不能直接互通。这样,广播报…...
Linux域名解析
1.hosts:windows c盘下面 Linux: /etc/hosts 作用:实现名字解析,主要为本地主机名、集群节点提供快速解析。平面式结构,集中式数据库。 缺点:不便于查询更新 2.DNS:域名系统 作用:实现名字解析(分层性,层次性) FQDN:完全合格域名/全称域…...

树形结构和列表的区别
树形结构和列表在数据组织、表示方式以及应用场景等方面存在明显的区别。 首先,树形结构是一种非线性的数据结构,表现为层次的嵌套结构。每个节点可以有多个子节点,这些子节点又可以有自己的子节点,形成一个层次分明的结构。这种一…...

Go中json的解析和反解析
在解析过程中,反向解析不包含其中的部分参数也不会报错,这是需要注意的一点 31 func main() { // E: main redeclared in this block 32 type A…...

SpringBoot+vue实现退出功能
目录 1. 创建点击事件 2. 编写退出逻辑 在Spring Boot 和 Vue.js 应用中实现退出功能,通常涉及到前端的用户界面操作和注销逻辑。 以下是实现退出功能的步骤: 1. 创建点击事件 在header.vue中创建一个点击事件 <span style"text-decoratio…...

Linux操作系统中管理磁盘的另外一种操作方式。即LVM——逻辑卷管理操作
在Linux操作系统中管理磁盘的一种方法名称——LVM,这种管理磁盘的优势。 1.使用LVM去管理磁盘可以在不影响原来数据的前提下去扩容磁盘空间或者是缩减磁盘空间。 在LVM中除了上层逻辑券可以扩容,下层的券组也可以扩容。 2.使用LVM管理的磁盘支持快照功…...

Lua 零基础入门
Lua 1.Lua是什么? 1.1 Lua的历史 Lua是由Roberto Ierusalimschy、Luiz Henrique de Figueiredo和Waldemar Celes于1993年创建的,当时他们是巴西里约热内卢天主教大学计算机图形技术组(Tecgraf)的成员。在开发Lua之前࿰…...
记录DemoApplication.java不变蓝问题
问题 解决方案 一、点击右下角加载 二、右键项目 勾选maven...
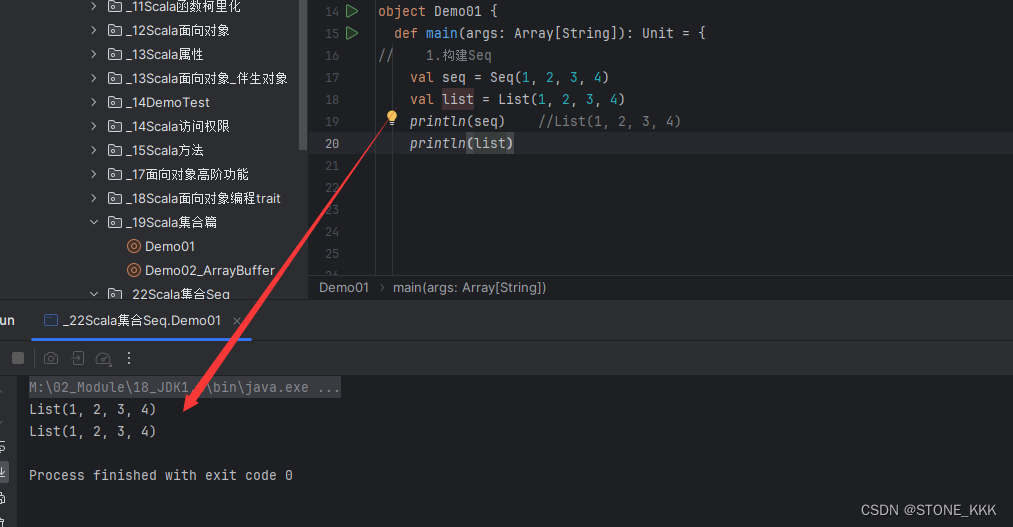
22_Scala集合Seq
文章目录 Seq序列1.构建集合2.List集合元素拼接&&集合拼接3.可变Seq&&List3.1 ListBuffer创建3.2 增删改查3.3 相互转化 Appendix1.Scala起别名2.Seq底层3.关于运算符操作: :4.空集合的表示 Seq序列 –Seq表示有序,数据可重复的集合 1.构建集合 …...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
