深入解析算法效率核心:时间与空间复杂度概览及优化策略

算法复杂度,即时间复杂度与空间复杂度,衡量算法运行时资源消耗。时间复杂度反映执行时间随数据规模增长的关系,空间复杂度表明额外内存需求。优化策略,如选择合适数据结构、算法改进、循环展开等,对于提升程序效率、减少资源占用至关重要,确保应用在不同场景下都能表现优异,特别是在处理大规模数据时,有效优化成为提升系统响应速度和用户体验的关键。
本文详细介绍了时间复杂度、空间复杂度的概念、常见的时间复杂度以及算法复杂度优化策略。
一、时间复杂度
基础概念
时间复杂度是算法分析中的一个重要概念,它用来评估算法执行时间与输入数据规模之间的增长关系。时间复杂度不是一个具体的运行时间,而是一个关于输入数据规模n的函数,用来描述随着n的增长,算法执行时间的增长趋势。
通常,时间复杂度用大O记号(O,即Big O notation)表示,关注的是算法执行的基本操作次数的上界。这样做的目的是为了简化分析,忽略常数因子和低阶项,专注于随着输入规模增加时,算法性能如何变化的趋势。
常见的时间复杂度
-
O(1) - 常数时间复杂度:算法的执行时间不随输入数据量的变化而变化,例如访问数组中的单个元素。
function constantTime(n) {return n[0]; // 访问数组第一个元素 } -
O(log n) - 对数时间复杂度:算法的执行时间与输入数据的对数成正比,常见于二分查找算法。
function binarySearch(arr, target) {let left = 0, right = arr.length - 1;while (left <= right) {let mid = Math.floor((left + right) / 2);if (arr[mid] === target) return true;if (arr[mid] < target) left = mid + 1;else right = mid - 1;}return false; } -
O(n) - 线性时间复杂度:算法的执行时间与输入数据量成正比,例如遍历数组。
function linearSearch(arr, target) {for (let i = 0; i < arr.length; i++) {if (arr[i] === target) return true;}return false; } -
O(n log n) - 线性对数时间复杂度:一些高效的排序算法,如快速排序、归并排序的时间复杂度为此。
function mergeSort(arr) {if (arr.length <= 1) return arr;const mid = Math.floor(arr.length / 2);const left = mergeSort(arr.slice(0, mid));const right = mergeSort(arr.slice(mid));return merge(left, right); }function merge(left, right) {// ...合并过程省略 } -
O(n^2) - 平方时间复杂度:常见于简单的排序和搜索算法,如冒泡排序、选择排序。
function bubbleSort(arr) {for (let i = 0; i < arr.length; i++) {for (let j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];}}} } -
O(2^n)、O(n!) - 指数级和阶乘级复杂度:这类算法在数据规模增大时非常慢,如递归解决旅行商问题、全排列问题。
评估方法
- 最坏情况、平均情况和最好情况:时间复杂度可以基于算法在不同情况下的表现来评估。
- 忽略低阶项和系数:在计算复杂度时,只保留最高阶项,并忽略系数和低阶项,因为当n足够大时,这些项对整体趋势影响不大。
通过理解时间复杂度,开发者可以预测算法在大规模数据上的性能表现,从而做出更优的算法选择或优化策略。
二、空间复杂度
算法的空间复杂度是衡量算法在运行过程中临时占用存储空间大小的一个量度,用来评估算法执行所需的内存资源。与时间复杂度相似,空间复杂度也使用大O记号表示,关注的是随着输入数据规模n增大,所需内存空间的增长趋势。
基础概念
- 定义:空间复杂度是对算法在运行过程中除了输入数据所占空间之外,额外需要的存储空间大小的度量。
- 计算:主要考虑变量数量、数据结构大小(如数组、链表等)、递归调用栈的深度等因素。
- 关注点:在内存资源有限的环境下,空间复杂度的优化尤为重要。
常见空间复杂度
-
O(1) - 常数空间复杂度:算法所需额外空间不随输入数据规模增长,例如简单的算术运算。
function add(a, b) {return a + b; } -
O(n) - 线性空间复杂度:算法所需空间与输入数据规模成正比,例如数组复制。
function arrayCopy(originalArray) {let newArray = new Array(originalArray.length);for (let i = 0; i < originalArray.length; i++) {newArray[i] = originalArray[i];}return newArray; } -
O(n^2) - 平方空间复杂度:空间需求与数据规模的平方成正比,常见于一些需要二维数组的算法中。
function generateMatrix(n) {let matrix = new Array(n);for (let i = 0; i < n; i++) {matrix[i] = new Array(n);}return matrix; } -
O(log n) - 对数空间复杂度:在分治算法中常见,如二叉树的深度。
-
O(n log n) - 线性对数空间复杂度:一些排序算法的空间复杂度,如归并排序(临时合并数组空间)。
-
O(n!) - 阶乘级空间复杂度:如解某些问题时使用的所有排列组合的存储。
递归空间复杂度
递归算法的空间复杂度还应考虑递归调用栈的深度,最坏情况下可能达到O(n),其中n是递归深度。
示例
function factorial(n) {if (n <= 1) return 1;return n * factorial(n - 1);
}
此递归函数factorial的空间复杂度为O(n),因为递归调用栈的深度最多为n层。
优化策略
- 重用空间:尽量复用已有空间,减少额外空间的分配。
- 迭代替代递归:在可能的情况下,使用迭代算法替换递归算法以减少递归调用栈的空间开销。
- 使用更高效的数据结构:选择更节省空间的数据结构,如使用位运算代替整型数组等。
理解空间复杂度有助于开发者在设计算法时更好地管理内存资源,特别是在内存敏感的环境(如嵌入式系统、移动设备)中。
三、算法复杂度优化策略
在JavaScript中,优化算法复杂度主要是为了减少算法执行时间和降低空间消耗,使之更加高效。优化策略往往围绕减少循环次数、优化数据结构、减少冗余计算等方面展开。以下是一些优化算法复杂度的策略及其示例:
1. 使用合适的数据结构
示例: 如果频繁执行查找操作,使用哈希表(在JavaScript中是对象或Map)代替数组或列表可以将查找复杂度从O(n)降低到O(1)。
// 优化前:数组查找
function findInArray(arr, target) {for (let i = 0; i < arr.length; i++) {if (arr[i] === target) return true;}return false;
}// 优化后:哈希表查找
function findWithMap(arr) {const map = new Map();for (const item of arr) {map.set(item, true);}return (target) => map.has(target);
}const arr = [1, 2, 3, 4, 5];
const finder = findWithMap(arr);
console.log(finder(3)); // 输出: true
2. 避免重复计算
示例: 使用动态规划避免子问题的重复计算,如斐波那契数列的计算。
// 未优化:重复计算
function fibonacci(n) {if (n <= 2) return 1;return fibonacci(n - 1) + fibonacci(n - 2);
}// 优化:使用动态规划
function fibonacciOptimized(n, memo = []) {if (memo[n] !== undefined) return memo[n];if (n <= 2) return 1;memo[n] = fibonacciOptimized(n - 1, memo) + fibonacciOptimized(n - 2, memo);return memo[n];
}console.log(fibonacciOptimized(10)); // 输出斐波那契数列第10项
3. 利用分治、贪心、回溯等高级算法策略
示例: 快速排序比冒泡排序效率高,因为它采用了分治策略。
// 冒泡排序(O(n^2))
function bubbleSort(arr) {for (let i = 0; i < arr.length; i++) {for (let j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];}}}return arr;
}// 快速排序(平均O(n log n))
function quickSort(arr) {if (arr.length <= 1) return arr;const pivotIndex = Math.floor(arr.length / 2);const pivot = arr.splice(pivotIndex, 1)[0];const left = [];const right = [];for (let i = 0; i < arr.length; i++) {if (arr[i] < pivot) {left.push(arr[i]);} else {right.push(arr[i]);}}return quickSort(left).concat([pivot], quickSort(right));
}console.log(quickSort([3, 0, 2, 5, -1, 4, 1])); // 输出排序后的数组
4. 减少循环中的操作
- 尽量减少循环内部的计算和函数调用。
- 避免在循环中创建新对象或数组,除非必要。
5. 利用缓存技术
对于计算密集型的操作,可以考虑使用缓存(如备忘录模式)存储中间结果,避免重复计算。
通过这些策略的应用,可以显著提升JavaScript算法的执行效率,降低资源消耗,特别是在处理大规模数据时效果更为明显。

相关文章:

深入解析算法效率核心:时间与空间复杂度概览及优化策略
算法复杂度,即时间复杂度与空间复杂度,衡量算法运行时资源消耗。时间复杂度反映执行时间随数据规模增长的关系,空间复杂度表明额外内存需求。优化策略,如选择合适数据结构、算法改进、循环展开等,对于提升程序效率、减…...
虚拟机装CentOS镜像
起先,是先安装一个VM虚拟机,再去官方网站之类的下载一些镜像,常见镜像有CentOS镜像,ubantu镜像,好像还有一个树莓还是什么的,软件这块,日新月异,更新太快,好久没碰&#…...
SpringCloud 集成consul,消费者报I/O error on GET request for...
创建消费者微服务,去调用生产者微服务的请求过程中,出现以下错误: 报错原因 因为在使用SpringCloudAlibaba中的Nacos框架时,自动整合了SpringCloud中的Ribbon框架中的负载均衡,因为微服务提供者有两个,在消…...

pytest的测试标记marks
引用打标的marks文档 Python的pytest框架(5)--测试标记(Markers)_pytest执行指定的marker-CSDN博客 https://www.cnblogs.com/pipile/p/12696226.html 给用例自定义打标签的代码示例 #coding:utf-8 import pytest pytest.mark.smoke def test_1():print("smoke的测试用…...
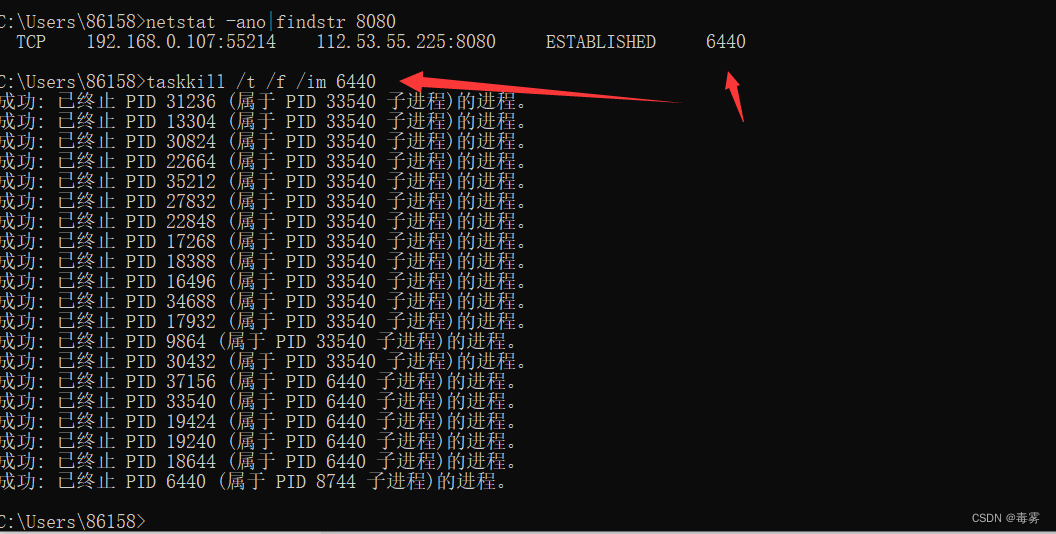
端口占用解决方法
1、查询端口 打开cmd命令提示符窗口,输入以下指令查询所有端口 netstat -ano //查询所有端口 netstat -ano|findstr 8080 //查询指定端口 2、杀死进程 taskkill /t /f /im 进程号(PID)...
Java毕设之基于springboot的医护人员排班系统
运行环境 开发语言:java 框架:springboot,vue JDK版本:JDK1.8 数据库:mysql5.7(推荐5.7,8.0也可以) 数据库工具:Navicat11 开发软件:idea/eclipse(推荐idea) 系统详细实现 医护类型管理 医护人员排班系统的系统管理员可以对医护类型添加修改删除以及…...
OpenCV4.8 VS2019 MFC编程出现的诡异现象
OpenCV4.8及OpenCV4.4 VS2019MFC编程在调用imred()函数时,debug X64试运行没问题。 release X64试运行时出现下面错误。 void CEasyPictureDlg::OnBnClickedOpen() {CFileDialog fdlg(TRUE, NULL, 0, OFN_HIDEREADONLY | OFN_OVERWRITEPROMP…...

游戏辅助 -- 三种分析角色坐标方法(CE、xdbg、龙龙遍历工具)
所用工具下载地址: https://pan.quark.cn/s/d54e7cdc55e6 在上次课程中,我们成功获取了人物对象的基址:[[[0xd75db8]1C]28],而人物血量的地址则是基址再加上偏移量278。 接下来,我们需要执行以下步骤来进一步操作&a…...

【VTKExamples::Rendering】第一期 TestAmbientSpheres(环境照明系数)
很高兴在雪易的CSDN遇见你 VTK技术爱好者 QQ:870202403 公众号:VTK忠粉 前言 本文分享VTK样例TestAmbientShperes,介绍环境照明系数对Actor颜色的影响,希望对各位小伙伴有所帮助! 感谢各位小伙伴的点赞+关注,小易会继续努力分享,一起进步! 你的点赞就是我的动…...

代码随想录leetcode200题之栈与队列
目录 1 介绍2 训练3 参考 1 介绍 本博客用来记录代码随想录leetcode200题中栈与队列部分的题目。 2 训练 题目1:232. 用栈实现队列 C代码如下, #include <stack>class MyQueue { private:stack<int> a;stack<int> b; //辅助栈 pu…...
使用Python实现2048小游戏
使用Python实现2048小游戏源码分享。实现效果如下所示。 实现效果图 游戏开始效果图 游戏结束效果图 部分源码截图 下载链接 基于如下的运行环境。运行需要安装tkinter /Library/Frameworks/Python.framework/Versions/3.7/bin/python/bin/python /Users/nihui/Documents/P…...

漏洞管理是如何在攻击者之前识别漏洞从而帮助人们阻止攻击的
漏洞管理 是主动查找、评估和缓解组织 IT 环境中的安全漏洞、弱点、差距、错误配置和错误的过程。该过程通常扩展到整个 IT 环境,包括网络、应用程序、系统、基础设施、软件和第三方服务等。鉴于所涉及的高成本,组织根本无法承受网络攻击和数据泄露。如果…...
LNMT部署jpress
LNMT部署jpress 环境要求: MySQL版本5.6/5.7 tomcat版本9.0.65 源码安装MySQL5.7版 //源码安装MySQL5.7版1关闭防火墙 2创建mysql用户 3上传mysql5.7包(https://downloads.mysql.com/archives/get/p/23/file/mysql-5.7.30-linux-glibc2.12-x86_64.tar.g…...

汽车软件研发工具链丨怿星科技新产品重磅发布
“创新引领未来”聚焦汽车软件新基建,4月27日下午,怿星科技2024新产品发布会在北京圆满举行!智能汽车领域的企业代表、知名大企业负责人、投资机构代表、研究机构代表齐聚现场,线上直播同步开启,共同见证怿星科技从单点…...

Faiss原理及使用总结
Faiss(Facebook AI Similarity Search)是一个用于高效相似性搜索和密集向量聚类的库。 一、原理 向量表示与相似度度量:在Faiss中,数据通常被表示为高维向量,这些向量可以来自深度学习模型的特征提取,也可…...

跨越智能建筑桥梁:西门子PLC无缝对接BACnet楼宇自动化系统化
智能楼宇每一个环节的互联互通都至关重要,而PLC(可编程逻辑控制器)作为自动化领域的基石,其与BACnet协议的融合无疑成为了构建智能楼宇神经系统的关键节点。今天,让我们深入探讨如何利用先进的PLC转BACnet协议网关&…...

景源畅信电商:抖音小店有哪些比较热门的宣传方法?
抖音小店的热门宣传方法,是许多商家关注的焦点。在数字化营销时代,有效的宣传手段不仅能提升品牌知名度,还能吸引潜在消费者,促进销售。以下是针对抖音小店热门宣传方法的详细阐述: 一、短视频内容营销 作为抖音的核心…...

兄弟DCP-7057激光打印机报错误代码EC检修及分析
故障描述: 兄弟DCP-7057激光打印机屏幕显示无法打印EC关闭电源,然后重新打开打印机。 故障检修及分析: 1、定影单元风扇的插线连接不良 检查定影单元风扇的插线连接并重新连接; 2、定影单元风扇故障 更换定影单元风扇;…...
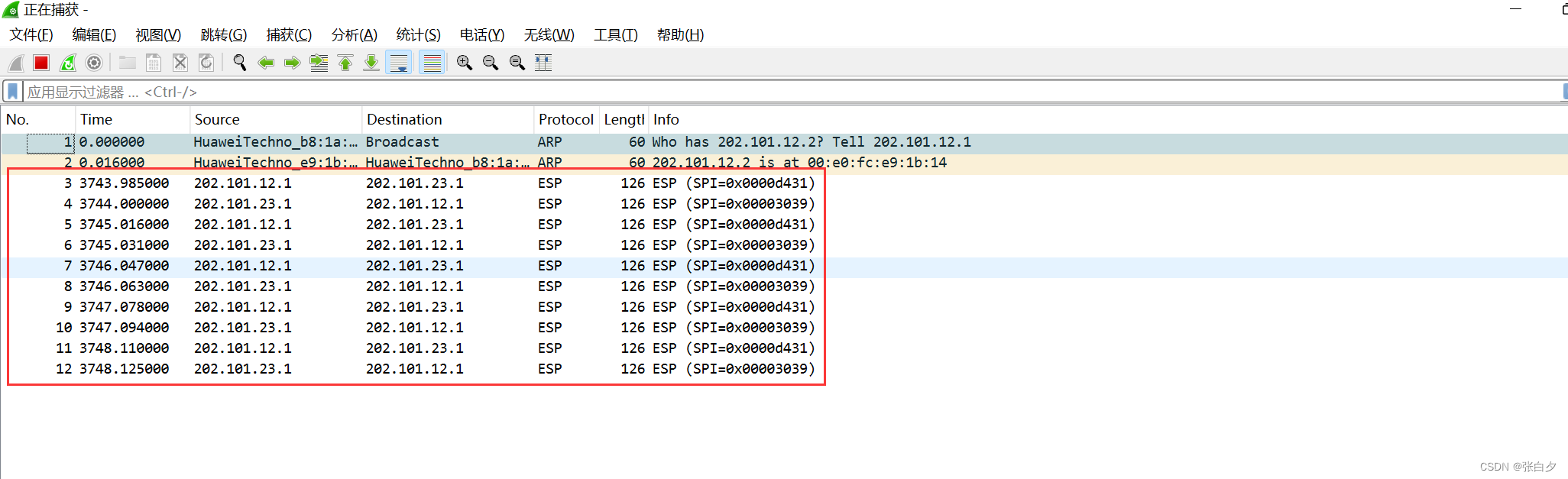
【华为】IPSec VPN手动配置
【华为】IPSec VPN手动配置 拓扑配置ISP - 2AR1NAT - Easy IPIPSec VPN AR3NATIPsec VPN PC检验 配置文档AR1AR2 拓扑 配置 配置步骤 1、配置IP地址,ISP 路由器用 Lo0 模拟互联网 2、漳州和福州两个出口路由器配置默认路由指向ISP路由器 3、进行 IPsec VPN配置&…...
)
面试题分享之Java集合篇(三)
注意:文章若有错误的地方,欢迎评论区里面指正 🍭 系列文章目录 面试题分享之Java基础篇(二)面试题分享之Java基础篇(三) 面试题分享之Java集合篇(一)、 面试题分享之Ja…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
