LeetCode热题100|动态规划Part.1|70.爬楼梯、118.杨辉三角、198.打家劫舍
70.爬楼梯
代码随想录原题,看这篇文章:C++动态规划Part.1|动态规划理论基础、509.斐波那契数、70.爬楼梯、746.使用最小花费爬楼梯
118.杨辉三角
题目链接:118.杨辉三角
一刷代码
时间复杂度和空间复杂度都造到 O ( n u m R o w s 2 ) O(numRows^2) O(numRows2)了。
基本思路就是先构造一个result存储最终的结果,然后定义一个dp数组来计算每一行的结果。
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> result;for (int i = 0; i < numRows; i++) {vector<int> dp(i + 1, 1); // 行的大小应为i+1if (i >= 2) { // 从第三行开始填充中间的数for (int j = 1; j < i; j++) {dp[j] = result[i - 1][j - 1] + result[i - 1][j]; // 正确使用result中的前一行}}result.push_back(dp);}return result;}
};
思路
很容易看到一个主要的性质:
杨辉三角中每个数字等于上一行的左右两个数字之和。
-
确定dp数组下标和含义
dp[i][j]等于第i行和第j列的值。 -
确定递推公式
递推公式很容易分析出来:
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
也就是每个数字等于上一行左右两个数字之和,但是需要注意的是, 每一行的最左边和最右边的数字必须是1. -
初始化dp数组
这里应该如何初始化呢?
最直接的方式就是直接全部初始化成1,因为每一行除了第一个和最后一个元素,我们都能通过递推公式进行推导 -
确定遍历顺序
在leetcode的题目展示上面已经看的很清楚了,
外循环从上往下遍历,内循环从左往右遍历。
这里需要注意的是,由于每一行的元素个数都是变化的,所以关于行的初始化一定要在外循环中处理。代码如下:
for (int i = 0; i < numRows; ++i) { //先遍历行dp[i].resize(i + 1); //将第i行的向量大小调整为i+1dp[i][0] = dp[i][i] = 1;for (int j = 1; j < i; +=j) { //再遍历列dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}
}
- 打印dp数组
还是比较简单的,这里就不写了。
CPP代码
其实思路还是很简单的,不过代码实现要一点小技巧,
- 在这里我们先创建一个大小为numRows的二维向量,其中每一行都是一个空的向量。在这种情况下,ret的初始状态是一个包含5行的二维向量,但每行都没有元素。
vector<vector<int>> dp(numRows);
- 然后我们在外循环中给每一行向量再调整大小,这样我们在原数组上做操作,空间复杂度一下就下来了。
for (int i = 0; i < numRows; ++i) {dp[i].resize(i + 1);...
}
总体代码如下:
class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> dp(numRows);for (int i = 0; i < numRows; ++i) {dp[i].resize(i + 1);dp[i][0] = dp[i][i] = 1;for (int j = 1; j < i; ++j) {dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}}return ret;}
};
198.打家劫舍
代码随想录原题,看这篇文章:C++动态规划Part8|198.打家劫舍、213.打家劫舍II、198.打家劫舍III
相关文章:

LeetCode热题100|动态规划Part.1|70.爬楼梯、118.杨辉三角、198.打家劫舍
70.爬楼梯 代码随想录原题,看这篇文章:C动态规划Part.1|动态规划理论基础、509.斐波那契数、70.爬楼梯、746.使用最小花费爬楼梯 118.杨辉三角 题目链接:118.杨辉三角 一刷代码 时间复杂度和空间复杂度都造到 O ( n u m R o w s 2 ) O(num…...
python 根据网址和关键词批量下载影像
最近用到了GLASS的LAI产品,但这个产品的文件夹分得很细,我需要的影像又有8个瓦片,一个一个点击很麻烦,于是探索了批量下载的方法 一、下载1幅 import requests import re import os import requests import re# 网页URLurl &…...
爬虫-无限debug场景 解决方式
解决无限debug 场景1 1. 鼠标右键 选择 continue to here(此处不停留)2. 鼠标右键 选择 edite breakpoint 设置 10 保证条件不成立 这行永远不执行3.方法置空 1. 方法调用加断点2. 控制台 setInterval function name() {}4. 替换文件 5. hoo…...

[链表专题]力扣206, 203, 19
1. 力扣206 : 反转链表 (1). 题 : 图略 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。示例 1:输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2:输入:head [1,2] 输出&#x…...

秋招后端开发面试题 - MySQL基础
目录 MySQL基础前言面试题MySQL 基础篇Mysql 的基础架构?MySQL 的长连接和短连接长连接引起的异常重启问题?说一下 MySQL 执行一条查询语句的内部执行过程?MySQL 查询缓存的功能有何优缺点?MySQL 的常用引擎都有哪些?I…...
力扣每日一题113:路径总和||
题目 中等 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1: 输入:root [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSu…...

Thinkphp5 中常见的session 操作方法
在 ThinkPHP 框架中,session 是用于在多个页面或请求之间存储用户信息的机制。以下是在 ThinkPHP 中进行 session 常见操作的一些示例: 启动 Session 在 ThinkPHP 中,通常不需要手动启动 Session,因为框架会在应用启动时自动处理…...
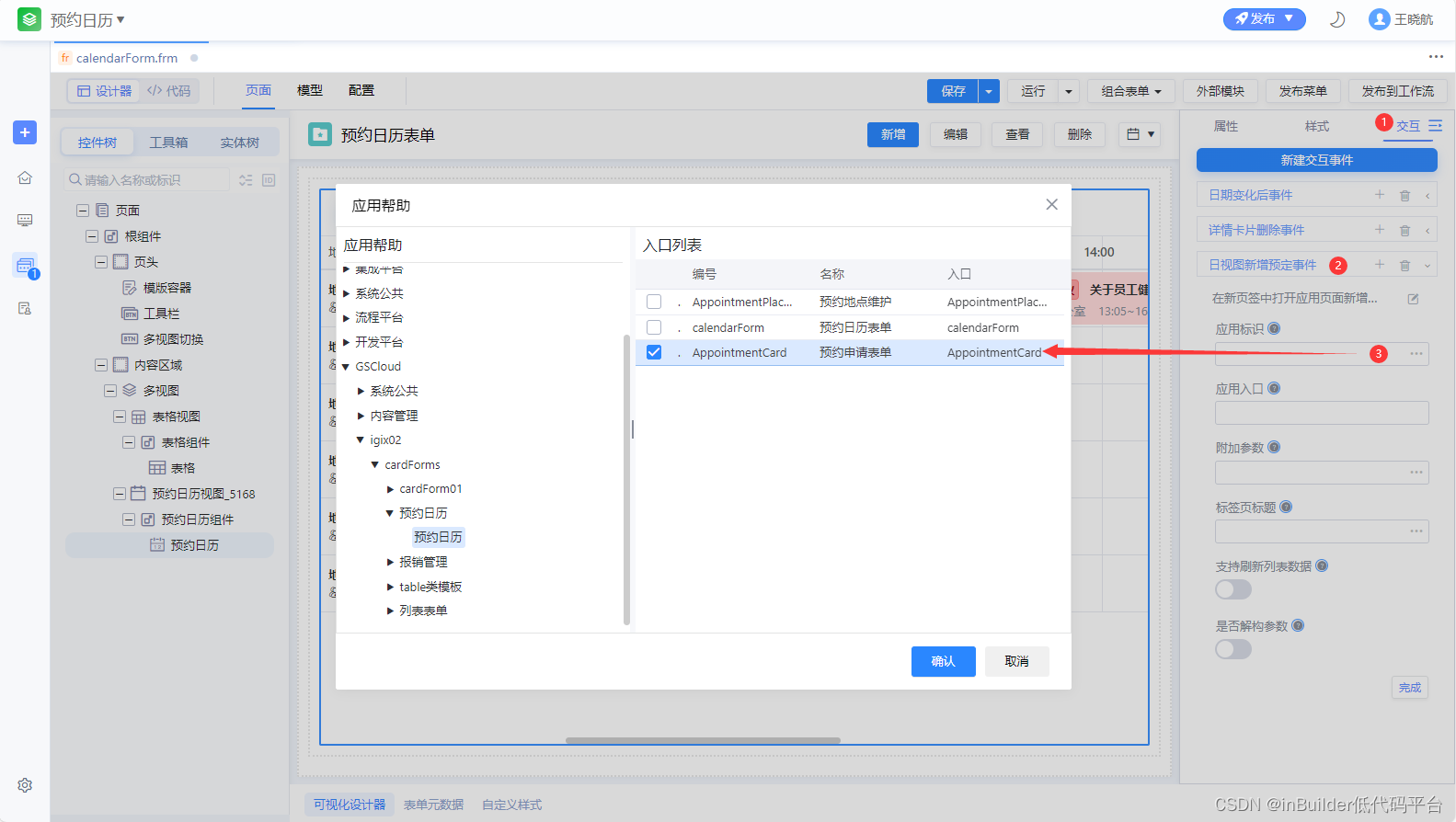
inBuilder 低代码平台新特性推荐 - 第十八期
今天来给大家带来的是inBuilder低代码平台特性推荐系列第十八期——表单设计器集成预约日历组件。 一、场景介绍 项目上希望用日历的形式展示某地点在一段时间内的预约记录,表单设计器新增支持创建日历预约视图,并配置预约属性。 二、运行效果 三、前…...

部署xwiki服务需要配置 hibernate.cfg.xml如何配置?
1. 定位 hibernate.cfg.xml 文件 首先,确保您可以在 Tomcat 的 XWiki 部署目录中找到 hibernate.cfg.xml 文件: cd /opt/tomcat/latest/webapps/xwiki/WEB-INF ls -l hibernate.cfg.xml如果文件存在,您可以继续编辑它。如果不存在ÿ…...
)
1376:信使(msner)
【解题思路】 每个哨所是一个顶点,哨所与哨所之间的通信线路为边,两哨所间通讯花费的时间为边的权值。记第一个哨所为顶点s,信息从第一个哨所传递到表示为顶点x的某哨所可能有多条路径,每条传送路径有一个花费的时间&…...
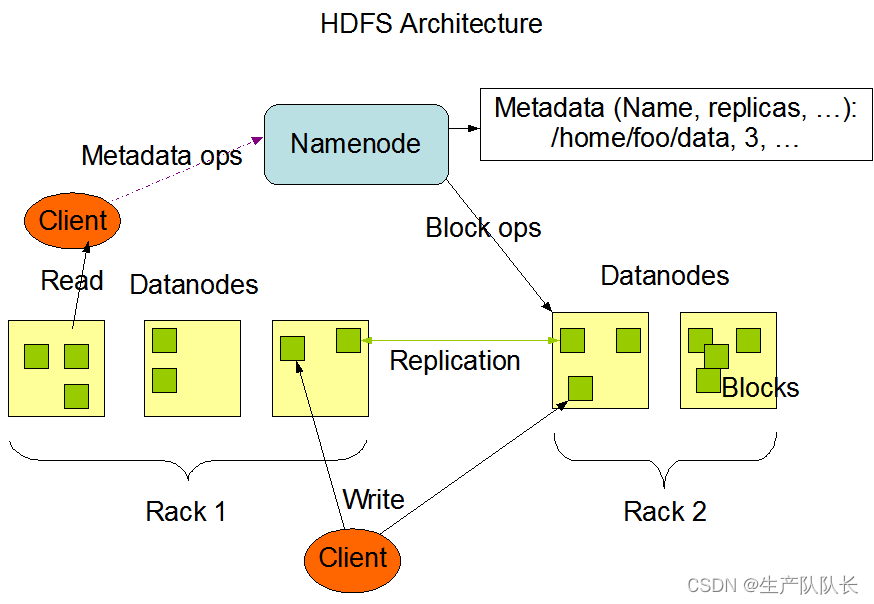
Hadoop3:HDFS的架构组成
一、官方文档 我这里学习的是Hadoop3.1.3版本,所以,查看的也是3.1.3版本的文档 Architecture模块最下面 二、HDFS架构介绍 HDFS架构的主要组成部分,是一下四个部分 1、NameNode(NN) 就是Master节点,它是集群管理者。 1、管…...

P2910 [USACO08OPEN] Clear And Present Danger S
Problem: P2910 [USACO08OPEN] Clear And Present Danger S 文章目录 思路解题方法复杂度Code 思路 这是一个图论问题,我们需要找到从一个城市到另一个城市的最短路径。我们可以使用Floyd-Warshall算法来解决这个问题。首先,我们需要构建一个距离矩阵&am…...

ES6 对象方面的新特性
ES6(ECMAScript 2015)为JavaScript语言增加了很多新特性,包括对象字面量属性的简写、计算属性名、方法的简写、对象的解构赋值、Object.assign()方法复制对象属性、Object.is()比较两个值等。以下是一些在ES6中经常使用的对象方法:…...
)
GO语言核心30讲 进阶技术 (第一部分)
原站地址:Go语言核心36讲_Golang_Go语言-极客时间 一、数组和切片 1. 两者最大的不同:数组的长度是固定的,而切片的长度是可变的。 2. 可以把切片看成是对数组的一层封装,因为每个切片的底层数据结构中,一定会包含一…...

[力扣题解]225. 用队列实现栈
题目:225. 用队列实现栈 思路 用一个队列模拟栈; 假设有数字:1,2,3; pop 队列里是这样的存的:3,2,1; 作为一个栈,应该弹出最后进来的那一个3&…...

Leetcode—2105. 给植物浇水 II【中等】
2024每日刷题(131) Leetcode—2105. 给植物浇水 II 实现代码 class Solution { public:int minimumRefill(vector<int>& plants, int capacityA, int capacityB) {int size plants.size();int i 0;int j size - 1;int capA capacityA;in…...

wordpress外贸建站公司歪建站新版网站上线
wordpress外贸建站公司 歪猫建站 歪猫WordPress外贸建站,专业从事WordPress多语言外贸小语种网站建设与外贸网站海个推广、Google SEO搜索引擎优化等服务。 https://www.waimaoyes.com/dongguan...

关于二手车系统学习--登录模块
1.样式1-17行 <div class="cheader"><div style="width: 80%;margin: 0 auto;line-height: 50px;padding-top: 10px"><el-row><el-col:span="5"style="font-size: 20px;cursor: pointer;color: #00ae66;font-weight: …...
若依生成代码的步骤
1.创建表,要有注释 2.导入表 3.创建主菜单 4.修改表 5.生成代码 6.把代码复制到自己的程序中:复制表、后端、前端 7.重启后端,如果有问题则clean 8.回到浏览器可以看到正常显示了生成的页面...

深度学习论文: LightGlue: Local Feature Matching at Light Speed
深度学习论文: LightGlue: Local Feature Matching at Light Speed LightGlue: Local Feature Matching at Light Speed PDF: https://arxiv.org/pdf/2306.13643 PyTorch代码: https://github.com/shanglianlm0525/CvPytorch PyTorch代码: https://github.com/shanglianlm0525/…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
