(贪心05) 无重叠区间 划分字母区间 合并区间
一、无重叠区间
力扣第435题
第一种方法:
个人思路:
按照区间左边界排序,然后从左开始遍历,每遍历到一个区间就要保证该区间之前的集合为不重叠区间(贪心,局部最优解)。
难点在于如何把新遍历到的区间整合为不重叠,分情况讨论。
代码如下:
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals, (a, b) -> {if(a[0] == b[0]) return a[1] - b[1];return a[0] - b[0];});int remove = 0;for(int i = 1; i < intervals.length; i++) {if(intervals[i][0] == intervals[i - 1][0]) {if(intervals[i][1] > intervals[i - 1][1]) {intervals[i][1] = intervals[i - 1][1];}remove ++;} else if(intervals[i][0] < intervals[i - 1][1]) {if(intervals[i][1] > intervals[i - 1][1]) {intervals[i][0] = intervals[i - 1][0];intervals[i][1] = intervals[i - 1][1];}remove ++;}}return remove;}
}时间复杂度:O(nlogn)
空间复杂度:O(1)
第二种方法:
思路:
统计不重叠区间,最后区间总和减去不重叠区间个数就等于重叠区间个数。
代码如下:
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals, (a,b)-> {return Integer.compare(a[0],b[0]);});int count = 1;for(int i = 1;i < intervals.length;i++){if(intervals[i][0] < intervals[i-1][1]){intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);continue;}else{count++;} }return intervals.length - count;}
}时间复杂度:O(nlogn)
空间复杂度:O(1)
二、划分字母区间
力扣第763题
思路:
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
代码如下:
class Solution {public List<Integer> partitionLabels(String s) {int[] hash = new int[27];for(int i = 0; i < s.length(); i++) {char c = s.charAt(i);hash[c - 'a'] = i;}List<Integer> list = new ArrayList<>();int left = 0;int right = 0;for(int i = 0; i < s.length(); i++) {right = Math.max(right, hash[s.charAt(i) - 'a']);if(i == right) {list.add(right - left + 1);left = i + 1;}}return list;}
}时间复杂度:O(n)
空间复杂度:O(1)
三、合并区间
力扣第56题
代码如下:
class Solution {public int[][] merge(int[][] intervals) {Arrays.sort(intervals, (a, b) -> {if(a[0] == b[0]) return a[1] - b[1];return a[0] - b[0];});List<int[]> list = new ArrayList<>();list.add(intervals[0]);int index = 0;for(int i = 1; i < intervals.length; i++) {if(intervals[i][0] <= list.get(index)[1]) {list.get(index)[1] = Math.max(intervals[i][1], list.get(index)[1]);} else {list.add(intervals[i]);index++;}}return list.toArray(new int[list.size()][]);}
}时间复杂度:O(nlogn);
空间复杂度:O(1);
相关文章:
 无重叠区间 划分字母区间 合并区间)
(贪心05) 无重叠区间 划分字母区间 合并区间
一、无重叠区间 力扣第435题 第一种方法: 个人思路: 按照区间左边界排序,然后从左开始遍历,每遍历到一个区间就要保证该区间之前的集合为不重叠区间(贪心,局部最优解)。 难点在于如何把新遍历…...
入门)
简单网络管理协议(SNMP)入门
目录 概述 SMI(对象命名、数据类型、编码方法) 对象命名 数据类型 编码方法 MIB(版本、分组、对象定义、变量访问) 版本 分组 对象定义 变量访问 SNMP 实现机制与报文分析 协议操作 报文格式 实现机制 验证分析 SN…...
1366 - 1372 题)
leetcode解题思路分析(一百五十七)1366 - 1372 题
通过投票对团队排名 现在有一个特殊的排名系统,依据参赛团队在投票人心中的次序进行排名,每个投票者都需要按从高到低的顺序对参与排名的所有团队进行排位。 排名规则如下: 参赛团队的排名次序依照其所获「排位第一」的票的多少决定。如果存在…...

药物代谢动力学学习笔记
一、基本概念 二、经典房室模型 三、非线性药物代谢动力学 四、非房室模型 五、药代动力学与药效动力学 六、生物等效性评价 七、生物样品分析方法 基本概念 生物样品:生物机体的全血、血浆、血清、粪便、尿液或其他组织的样品 特异性,specificity&…...
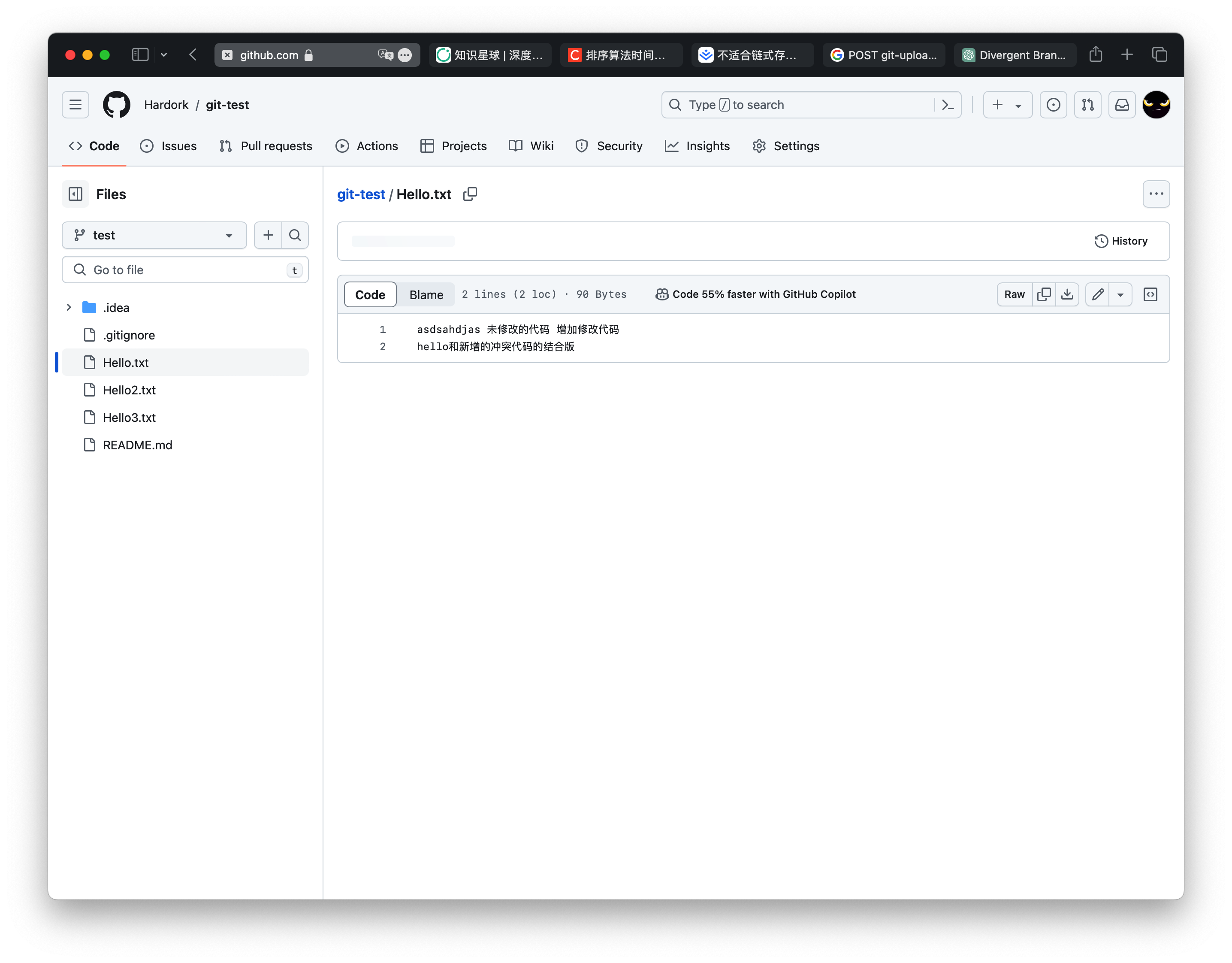
IDEA中git的常用操作(保姆级教学)
IDEA中git的常用操作(保姆级教学) 以下是git的工作原理,觉得繁琐的可以跳过不看 Workspace:工作区 (平时存放代码的地方) Index / Stage:暂存区(用于临时存放存放你的改动,事实上就是一个文件&…...
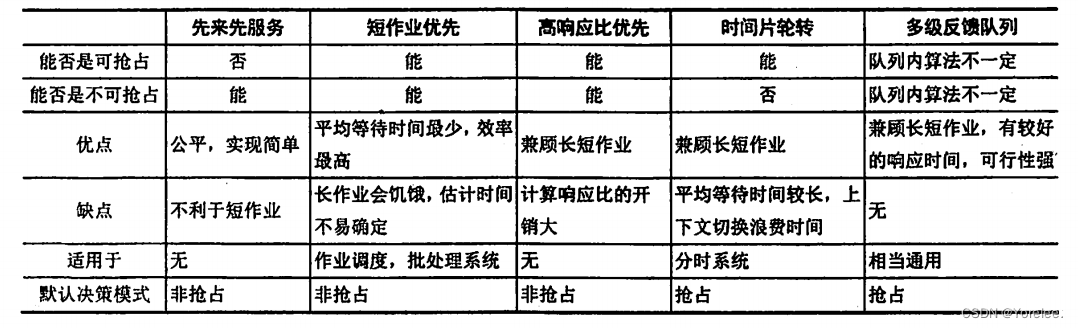
保研面试408复习 3——操作系统
文章目录 1、操作系统一、进程有哪几种状态,状态之间的转换、二、调度策略a.处理机调度分为三级:b.调度算法 标记文字记忆,加粗文字注意,普通文字理解。 为什么越写越少? 问就是在打瓦。(bushi) 1、操作系统 一、进程…...
)
【代码随想录37期】Day02 有序数组的平方、长度最小的子数组、螺旋矩阵Ⅱ(施工中)
有序数组的平方 977. 有序数组的平方 - 力扣(LeetCode) v1.0:直接暴力 4分半做出来,用sort api class Solution { public:vector<int> sortedSquares(vector<int>& nums) {vector<int> result;for(int i 0; i<…...
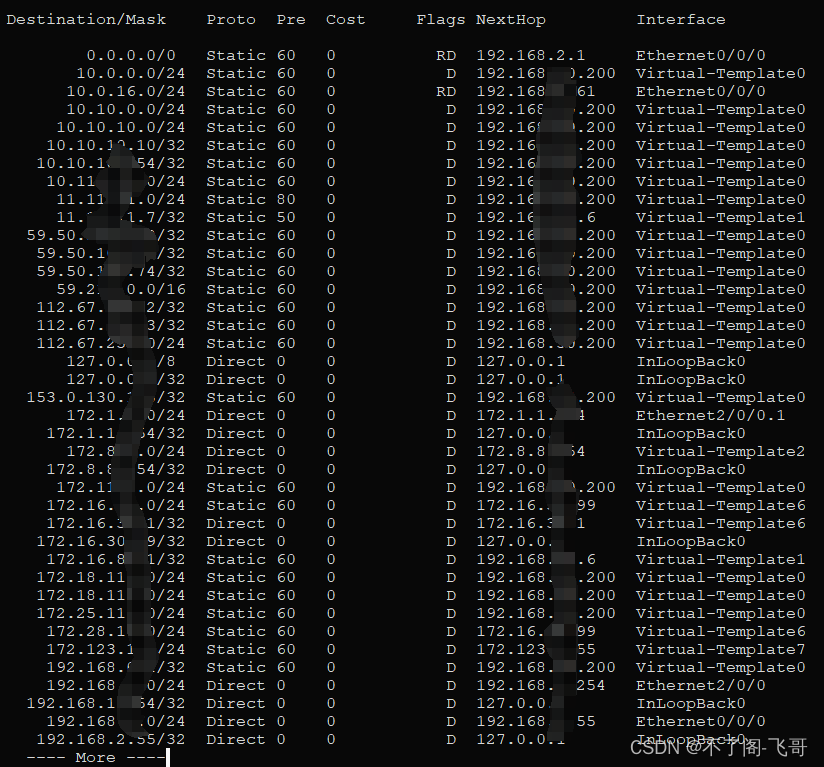
通俗的理解网关的概念的用途(三):你的数据包是如何到达下一层的
其实,这一章我写不好,因为这其中会涉及到一些计算和一些广播等概念,本人不善于此项。在此略述,可以参考。 每台设备的不同连接在获得有效的IP地址后,会根据IP地址的规则和掩码的规则,在操作系统和交换机&a…...
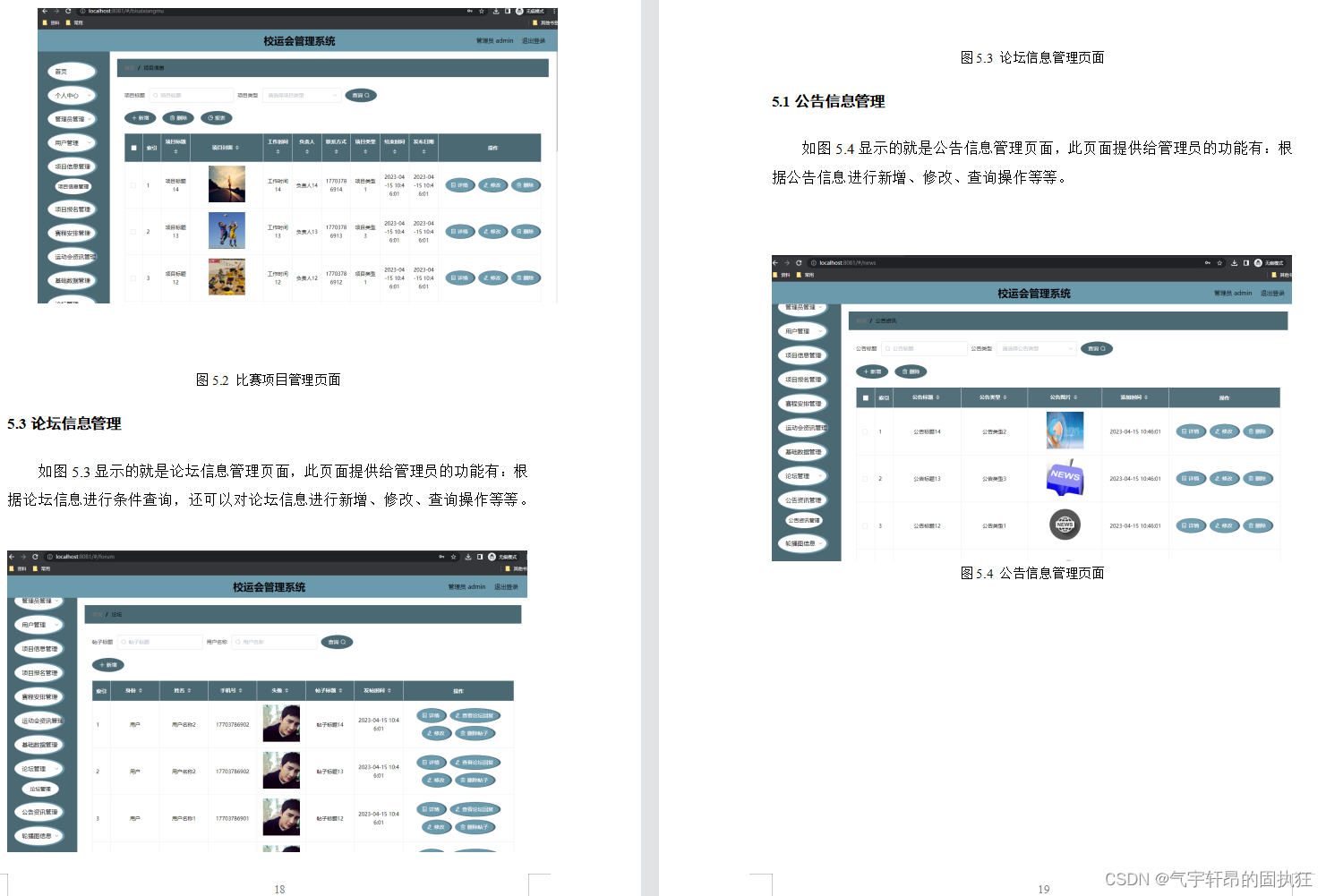
基于Springboot的校运会管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的校运会管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&a…...
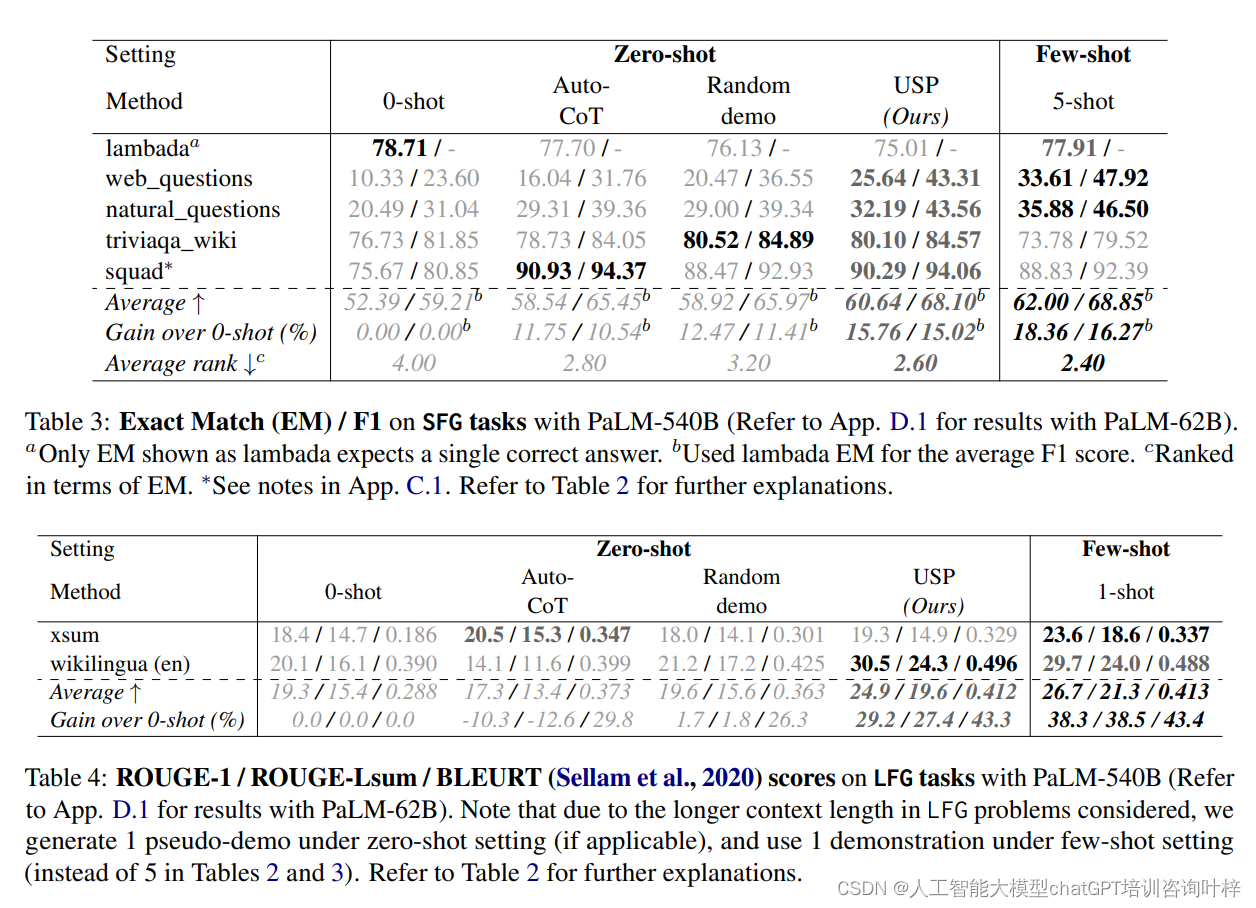
USP技术提升大语言模型的零样本学习能力
大语言模型(LLMs)在零样本和少样本学习能力上取得了显著进展,这通常通过上下文学习(in-context learning, ICL)和提示(prompting)来实现。然而,零样本性能通常较弱,因为缺…...
)
前端安全防护实战:XSS、CSRF防御与同源策略详解(react 案例)
前端安全防护实战中,主要涉及三个方面:XSS (Cross-Site Scripting) 攻击的防御、CSRF (Cross-Site Request Forgery) 攻击的防御,以及浏览器的同源策略。以下是这三个方面的详细说明: XSS 防御详解 XSS 概述 XSS攻击是一种让攻…...
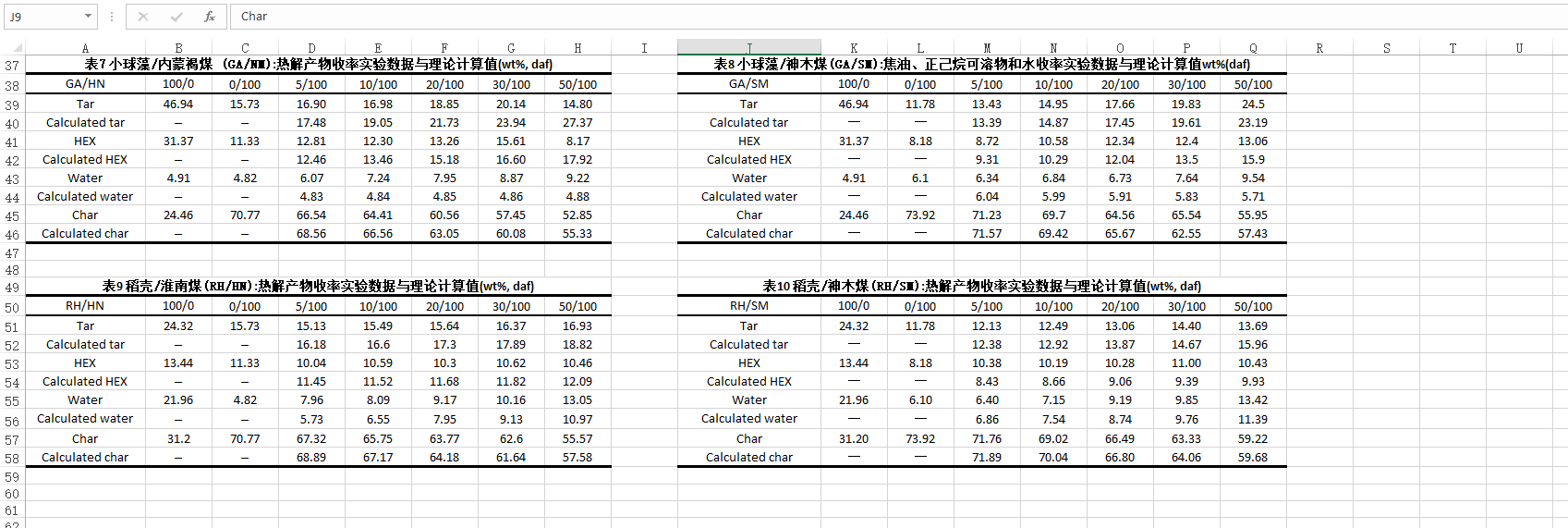
2024C题生物质和煤共热解问题的研究 详细思路
背景 随着全球能源需求的不断增长和对可再生能源的追求,生物质和煤共热解作为一种潜在的能源转化技术备受关注。生物质是指可再生能源,源自植物和动物的有机物质,而煤则是一种化石燃料。** 在共热解过程中,生物质和煤在高温和缺氧…...

智慧旅游引领未来风尚,科技助力旅行更精彩:科技的力量推动旅游业创新发展,为旅行者带来更加便捷、高效和智能的旅行服务
目录 一、引言 二、智慧旅游的概念与特点 (一)智慧旅游的概念 (二)智慧旅游的特点 三、科技推动旅游业创新发展 (一)大数据技术的应用 (二)人工智能技术的应用 (…...
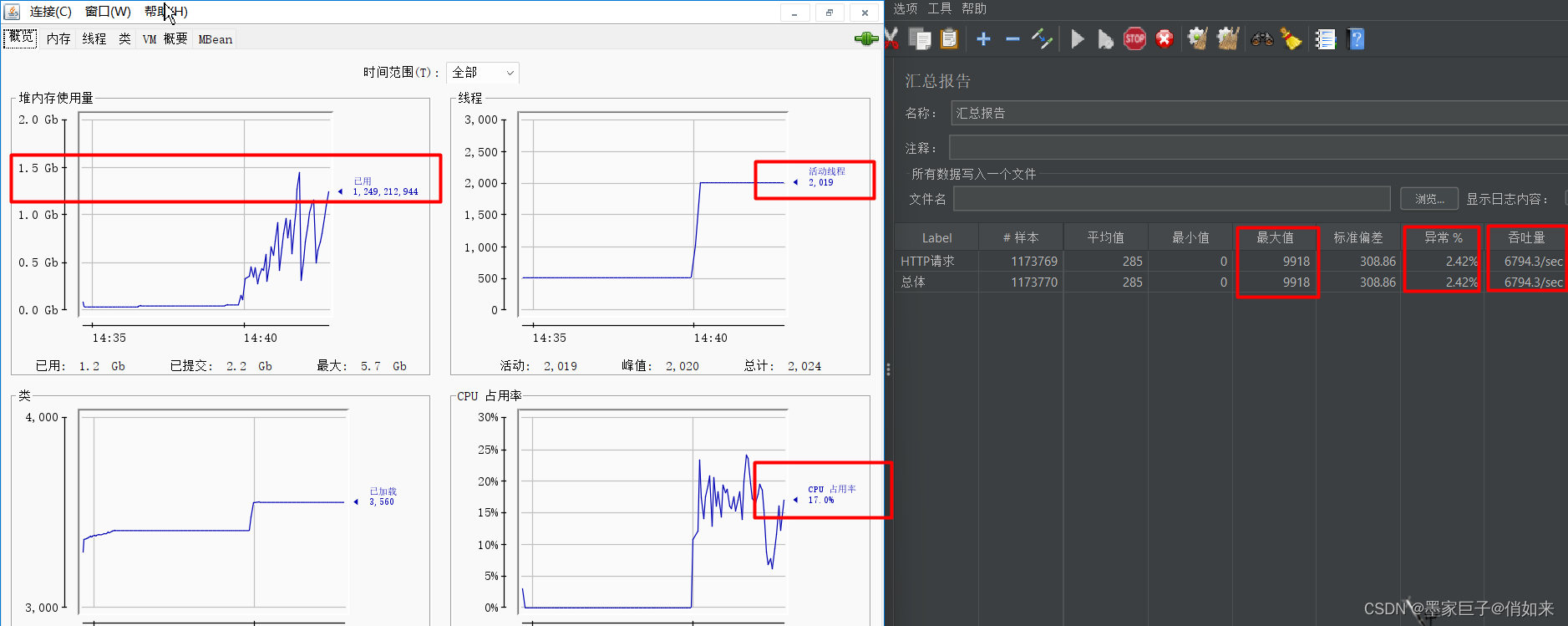
十.吊打面试官系列-Tomcat优化-通过压测Tomcat调优实战
前言 上一篇文章我们讲解了一下Tomcat底层的结构和执行原理,我们需要重点去掌握的是Tomcat的高内聚低耦合的设计,以及责任链模式,以及Tomcat NIO编程模式,这些是Tomcat比较核心的点,本篇文章我们将对Tomcat的参数做一…...
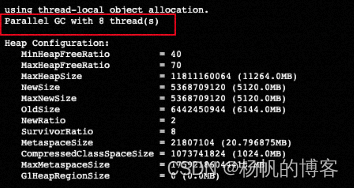
JVM调优—减少FullGC
背景 最近负责了一个审批流程新项目,带领了几个小伙伴,哼哧哼哧的干了3个月左右,终于在三月底完美上线了,好消息是线上客户用的很丝滑,除了几个非常规的业务提单之外,几乎没有什么大的问题,但是…...

力扣 256. 粉刷房子 LCR 091. 粉刷房子 python AC
动态规划 class Solution:def minCost(self, costs):row, col len(costs), 3dp [[0] * col for _ in range(row 1)]for i in range(1, row 1):for j in range(col):dp[i][j] costs[i - 1][j - 1]if j 0:dp[i][j] min(dp[i - 1][1], dp[i - 1][2])elif j 1:dp[i][j] m…...
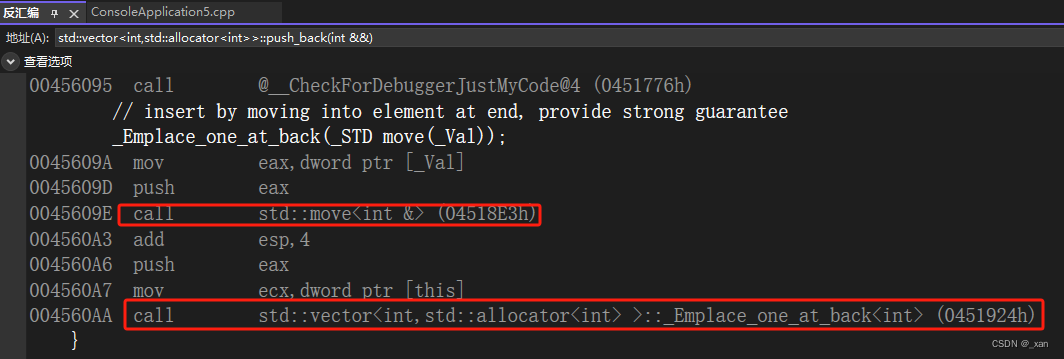
C++STL细节,底层实现,面试题04
文章目录 19. STL19.1. 序列容器19.1.1. vector19.1.1.1. 底层实现和特点19.1.1.2. 常用函数19.1.1.3. emplace_back() vs push_back() 19.1.2. array19.1.2.1. 底层实现和特点19.1.2.2. 常用函数 19.1.3. deque19.1.3.1. 底层实现和特点19.1.3.2. 常用函数 19.1.4 list19.1.4.…...

Linux查看Oracle数据库的环境变量
Linux查看Oracle数据库的环境变量 在Linux上查看Oracle数据库的环境变量,通常涉及检查当前shell会话中已设置的环境变量。这些环境变量可能包括ORACLE_HOME、ORACLE_SID、PATH(可能包含Oracle二进制文件的路径)等。 以下是几种方法来查看这…...
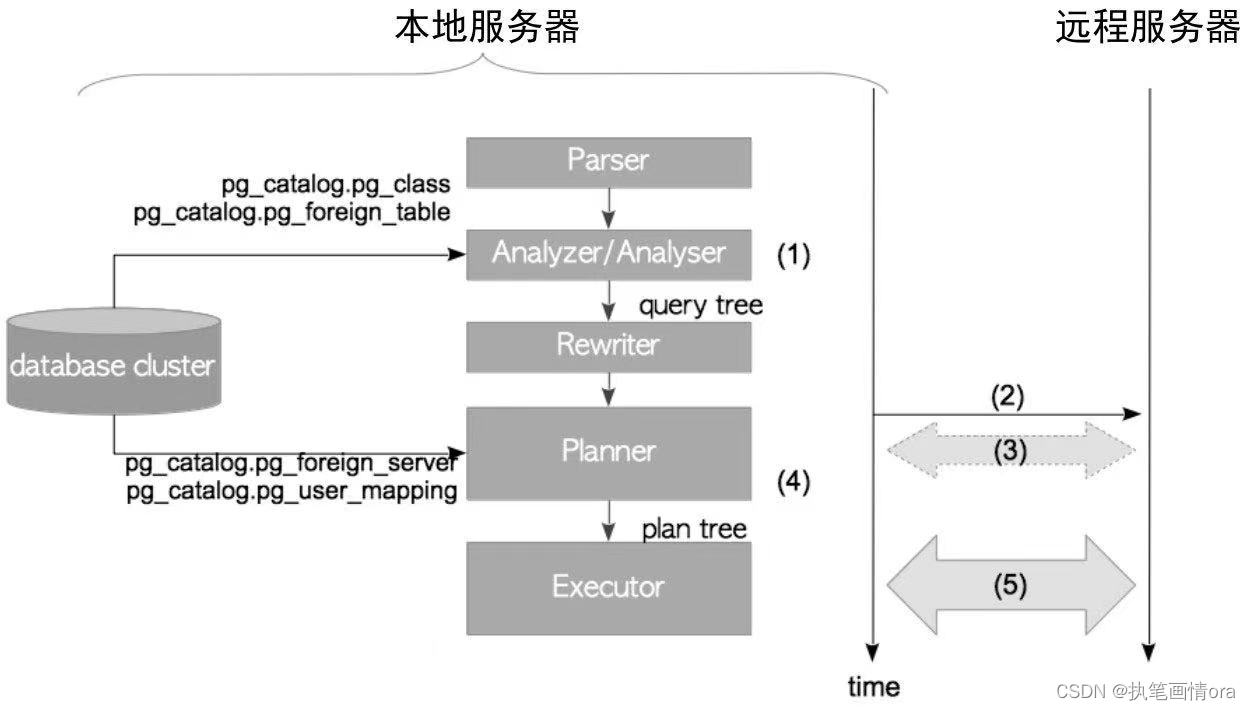
pg数据库学习知识要点分析-1
知识要点1 对象标识OID 在PostgreSQL内部,所有的数据库对象都通过相应的对象标识符(object identifier,oid)进行管理,这些标识符是无符号的4字节整型。数据库对象与相应oid 之间的关系存储在对应的系统目录中…...
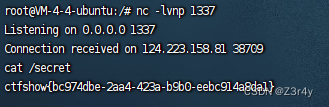
【Web】CTFSHOW 七夕杯 题解
目录 web签到 easy_calc easy_cmd web签到 CTF中字符长度限制下的命令执行 rce(7字符5字符4字符)汇总_ctf中字符长度限制下的命令执行 5个字符-CSDN博客7长度限制直接梭了 也可以打临时文件RCE import requestsurl "http://4ae13f1e-8e42-4afa-a6a6-1076acd08211.c…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
