2022CCPC女生赛(补题)(A,C,E,G,H,I)
迟了好久的补题,,现在真想把当时赛时的我拉出来捶一拳
排序大致按照题目难度。
C. 测量学

思路:直接循环遍历判断即可,注意角度要和2π取个最小值。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 1e5 + 5;
const double PI = acos(-1);
int n;
double ang, r[N];;int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> n >> r[0] >> ang;double ans = 1e18;for(int i = 1; i <= n; i ++) {std::cin >> r[i];}ang = std::min(ang, 2 * PI - ang);for(int i = 0; i <= n; i ++) {double res = (r[0] - r[i]) * 2 + r[i] * ang;ans = std::min(ans, res);}std::cout << std::fixed << std::setprecision(6) << ans << '\n';return 0;
}A. 减肥计划

思路:由k的范围,容易想到k很大的时候情况:找到序列最靠前且最大的数输出即可。对于剩下的情况,k的范围较小,将原数组复制一遍,处理一个前缀最大的数组,遍历寻找一个位置,满足这个位置及之前的最大值是他自己,并且后面k -1位没有比它更大的。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 2e6 + 5;
int n, k;
int a[N], pre[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> n >> k;int pos = -1, num = -1;for(int i = 1; i <= n; i ++) {std::cin >> a[i];a[i + n] = a[i];if(a[i] > num) {num = a[i], pos = i;}}if(k >= n - 1) {std::cout << pos << '\n';return 0;}for(int i = 1; i <= 2 * n; i ++) {if(a[i] > pre[i - 1]) pre[i] = a[i];elsepre[i] = pre[i - 1];}for(int i = 1; i <= 2 * n; i ++) {if(pre[i] == a[i] && pre[k + i - 1] == a[i]) {pos = i;break;}}std::cout << pos << '\n';return 0;
}E. 睡觉

思路:主要是分情况讨论。我们经过一次循环,可以得到一个数字x1,由x1和原来的x的大小情况分类:
(1)x1小于x,说明每经过一首歌的影响,x都会减小,那么一定存在若干遍后,x小到满足条件;
(2)x1大于x,说明每经过一首歌的影响,x都会变大,那若存在满足情况的区间,那一定是在第一个区间最有可能满足条件,只需要在第一个区间内判断一下即可。
(3)x1等于x,这样可以想到原来x的性质,如果原来是大于k的,那情况和第二种情况类似,判断第一个区间即可;但是若是原来是等于k的,那极有可能第一段满足条件的区间和最后一段满足条件的区间的和是满足大于等于t的,所以要处理连续两个区间,当然要注意t的大小,如果t是大于等于n的,那必须两个个区间内的最大值要大于n才行。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
#define int long long
const int N = 2e6 + 5;
int T, x, t, k, n, d;
int a[N];signed main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> T;while(T --) {std::cin >> x >> t >> k >> n >> d;x -= k;int original = x;int cnt = 0, max = -1;;for(int i = 1; i <= n; i ++) {std::cin >> a[i];if(a[i] <= d)a[i] = -1;elsea[i] = 1;a[i + n] = a[i];x += a[i];if(x <= 0) cnt ++;elsecnt = 0;max = std::max(max, cnt);}if(x < original) {std::cout << "YES" << '\n';continue;}if(x > original) {std::cout << (max >= t ? "YES" : "NO") << '\n';continue;}if(original > 0) {std::cout << (max >= t ? "YES" : "NO") << '\n';continue;}std::vector<int> vec;x = original;cnt = 0;for(int i = 1; i <= n; i ++) {x += a[i];if(x <= 0) {cnt ++;}else {vec.push_back(cnt);cnt = 0;}}vec.push_back(cnt);vec.push_back(vec[0] + vec[vec.size() - 1]);max = *max_element(vec.begin(), vec.end());t = std::min(t, n);std::cout << (max >= t ? "YES" : "NO") << '\n';}return 0;
}G. 排队打卡

思路:按照题意模拟即可,注意给出的数据分段,不要搞错了边界。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
#define int long long
const int N = 5e5 + 5;
int t, n, m, k;struct node {int t, x;
} e[N];bool cmp(node a, node b) {if(a.t < b.t) return true;else return false;
}signed main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);int sum = 0, pos = -1;std::cin >> t >> n >> m >> k;for(int i = 1; i <= m; i ++) {std::cin >> e[i].t >> e[i].x;}std::sort(e + 1, e + 1 + m, cmp);for(int i = 1; i <= m; i ++) {if(e[i].t > t && pos == -1) pos = i - 1;}if(!pos) {if(n) {std::cout << "Wrong Record" << '\n';return 0;}}else {sum = e[1].x;for(int i = 2; i <= pos; i ++) {sum -= std::min(sum, k * (e[i].t - e[i - 1].t));sum += e[i].x;}sum -= std::min(sum, k * (t - e[pos].t));if(sum != n) {std::cout << "Wrong Record" << '\n';return 0;}}int last = t, cnt = 5e18, ans;for(int i = pos + 1; i <= m; i ++) {sum -= std::min(sum, k * (e[i].t - last));sum += e[i].x;last = e[i].t;int res = (int)ceil((sum + 1) * 1.0 / (double)k);if(res <= cnt) {cnt = res;ans = e[i].t;}}std::cout << ans << ' ' << cnt << '\n';return 0;
}os:现在写来感觉这个题比E要简单,按照题意写就行了,也没啥需要思考的,为啥当时就没做出来呢
I. 宠物对战

思路:其实看题目可以知道是一个比较典的dp问题。可以这样考虑,令f[i][0/1]表示处理到第i个字母,是由A中的字符串还是由B中的字符串组成的。可以考虑循环枚举最后到的位置,和这一整个字符串最后一个子字符串的开始位置,判断这个子字符串是否出自A或B组中,若是,则可以更新:
f[i][1/0] = min(f[i][1/0], f[j - 1][0/1] + 1);
而对于子字符串是否存在于A或者B组中,可以采用Trie树或者字符串哈希来处理,在这里我用的是字典树,但是在查询的时候加入了一点优化,如果直接查询的话会T飞欸。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
#define INF 0x3f3f3f3f
const int N = 5e5 + 5;
int n, m;
std::string a[N], b[N], s;
int f[N][2];struct Trie {int idx = 0;int mp[N][26], cnt[N];void insert(std::string s) {int p = 0;for(int i = 0; i < s.length(); i ++) {int u = s[i] - 'a';if(!mp[p][u]) mp[p][u] = ++ idx;p = mp[p][u];}cnt[p] ++;}
}A, B;int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> n;for(int i = 1; i <= n; i ++) {std::cin >> a[i];A.insert(a[i]);}std::cin >> m;for(int i = 1; i <= m; i ++) {std::cin >> b[i];B.insert(b[i]);}std::cin >> s;int len = s.length();s = ' ' + s;memset(f, INF, sizeof(f));f[0][1] = f[0][0] = 0;for(int i = 0; i <= len; i ++) {if(f[i][0] < INF) {int p = 0;for(int j = i + 1; j <= len; j ++) {int u = s[j] - 'a';if(A.mp[p][u]) {p = A.mp[p][u];if(A.cnt[p]) {f[j][1] = std::min(f[j][1], f[i][0] + 1);}}else break;}}if(f[i][1] < INF) {int p = 0;for(int j = i + 1; j <= len; j ++) {int u = s[j] - 'a';if(B.mp[p][u]) {p = B.mp[p][u];if(B.cnt[p]) {f[j][0] = std::min(f[j][0], f[i][1] + 1);}}else break;}}}int ans = std::min(f[len][1], f[len][0]);std::cout << (ans == INF ? -1 : ans) << '\n';return 0;
}os:学弟给的优化方法,tqlllllllll
H. 提瓦特之旅

思路:如果说对于每个询问都跑一次最短路的话,那必然会t,想办法通过离线预处理部分东西来降低部分时间复杂度。所以可以通过预处理数组dis[i][j],表示经过i个点到达j的最短路径,这样在每次询问的时候就可以在O(n * q)的复杂度内得到答案。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
typedef std::pair<int, int> PII;
const int N = 505;
int n, m, q, x, t;
ll dis[N][N];
std::vector<PII> vec[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> n >> m;for(int i = 1; i <= m; i ++) {int u, v, w;std::cin >> u >> v >> w;vec[u].push_back({v, w});vec[v].push_back({u, w});}for(int i = 0; i <= n; i ++) {for(int j = 0; j <= n; j ++) {dis[i][j] = 3e18;}}dis[0][1] = 0;for(int i = 1; i <= n; i ++) {for(int j = 1; j <= n; j ++) {for(auto [u, w] : vec[j]) {dis[i][j] = std::min(dis[i][j], dis[i - 1][u] + w);}}}std::cin >> q;while(q --) {std::cin >> t;ll sum = 0, ans = 3e18;for(int i = 1; i < n; i ++) {std::cin >> x;sum += x;ans = std::min(ans, dis[i][t] + sum);}std::cout << ans << '\n';}return 0;
}os:个人感觉这个题比前一个好写很多欸,但是可能就是怎样预处理卡住了吧QWQ
这次让我没想到的是和前几年难度差别这么大,感觉大概到了省赛难度吧,明年加油哇
相关文章:

2022CCPC女生赛(补题)(A,C,E,G,H,I)
迟了好久的补题,,现在真想把当时赛时的我拉出来捶一拳排序大致按照题目难度。C. 测量学思路:直接循环遍历判断即可,注意角度要和2π取个最小值。AC Code:#include <bits/stdc.h>typedef long long ll; const int…...

【Nginx】Nginx的安装配置
环境说明系统:Centos 7一、编译安装Nginx官网下载地址nginx: download#安装依赖 [rootnginx nginx-1.22.1]# yum install gcc pcre pcre-devel zlib zlib-devel -y #从官网下载Nginx安装包,并进行解压、编译、安装 [rootnginx ~]# wget https://nginx.or…...

数学小课堂:统计时有效地筛选数据
文章目录引言I 被爆冷门的原因II 统计时有效地筛选数据2.1 统计数据的常见问题2.2 大数据的特征2.3 有效筛选数据的原则引言 在博弈论中很多结果有发生的概率,而概率这件事只是估计出来的,并不准确。因此,一旦加入博弈的选手多了之后&#x…...

MySQL安装优化
hello,大家好,我是小鱼 本文主要通过针对 MySQL Server(mysqld)相关实现机制的分析,得到一些相应的优化建议。主要 涉及 MySQL 的安装以及相关参数设置的优化,但不包括 mysqld 之外的比如存储引擎相关的参…...

RocketMQ系列开篇
RocketMQ系列开篇 今天开始学习RocketMQ相关系列源码。我会带着自己的目的去学习源码。所以不会像一般的技术博客一样,写一个完整的流程,介绍每一步干了啥。而是提出一个问题,然后去看代码里面是怎么实现的。说明一下,本次系列我…...
logback无法删除太久远的日志文件?logback删除日志文件源码分析
logback无法删除太久远的日志文件?logback删除日志文件源码分析 最近发现logback配置滚动日志,但是本地日志文件甚至还有2年前的日志文件,服务器是却是正常的! 网上搜索了一波没有发现,只找到说不能删除太久远的旧日志…...

【MyBatis-Plus】基于@Version注解的乐观锁实现
引入mybatis-plus依赖,注意这里的版本要求 since 3.4.0;(3.4.1,3.4.2已测) 3.2.0肯定是不支持的,无法引入MybatisPlusInterceptor; 乐观锁 当要更新一条记录的时候,希望这条记录没有被别人更新…...
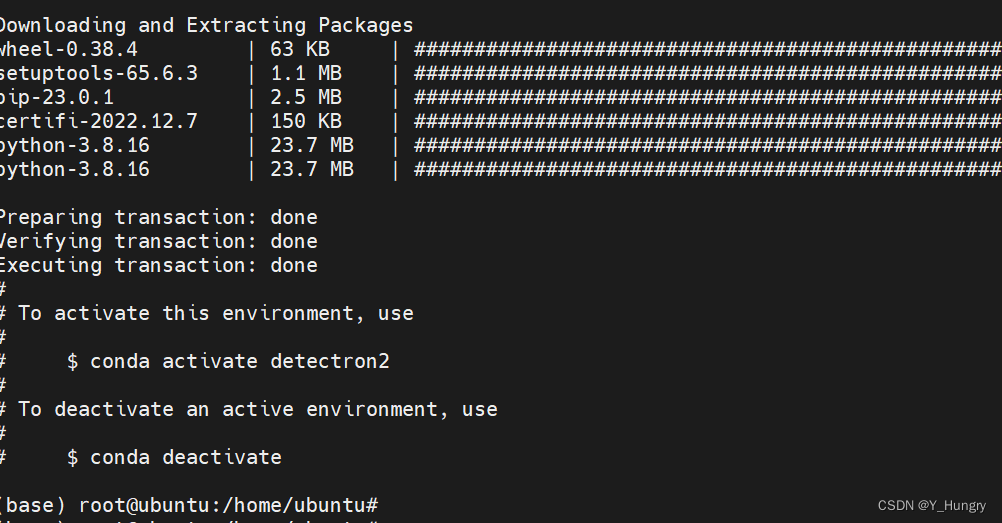
ubuntu20.04搭建detectron2环境
Ubuntu22.04安装Cuda11.3 Linux下驱动安装 # 以下命令按顺序执行 sudo apt update && sudo apt upgrade -y # or sudo apt update # 查看显卡信息 ubuntu-drivers devices sudo ubuntu-drivers autoinstall # or sudo apt install nvidia-driver-510 reboot nvidia-s…...
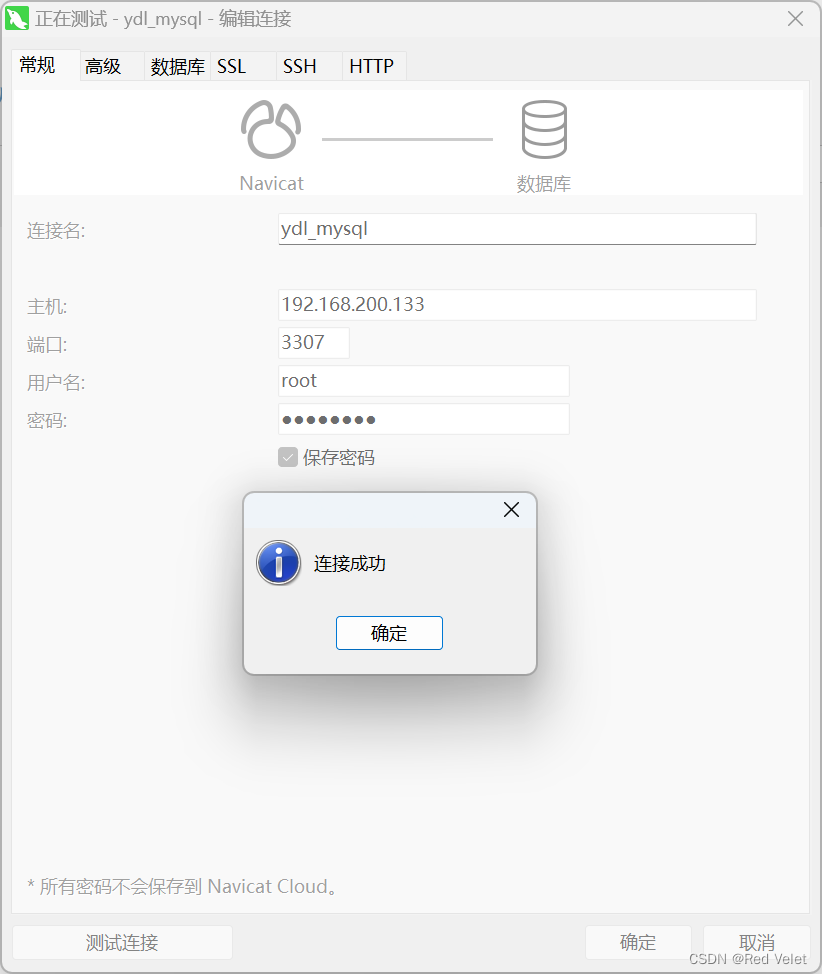
Navicate远程连接Linux上docker安装的MySQL容器
Navicate远程连接Linux上docker安装的MySQL容器失败 来自:https://bluebeastmight.github.io/ 问题描述:windows端的navicat远程连接不上Linux上docker安装的mysql(5.7版本)容器,错误代码10060 标注: 1、…...
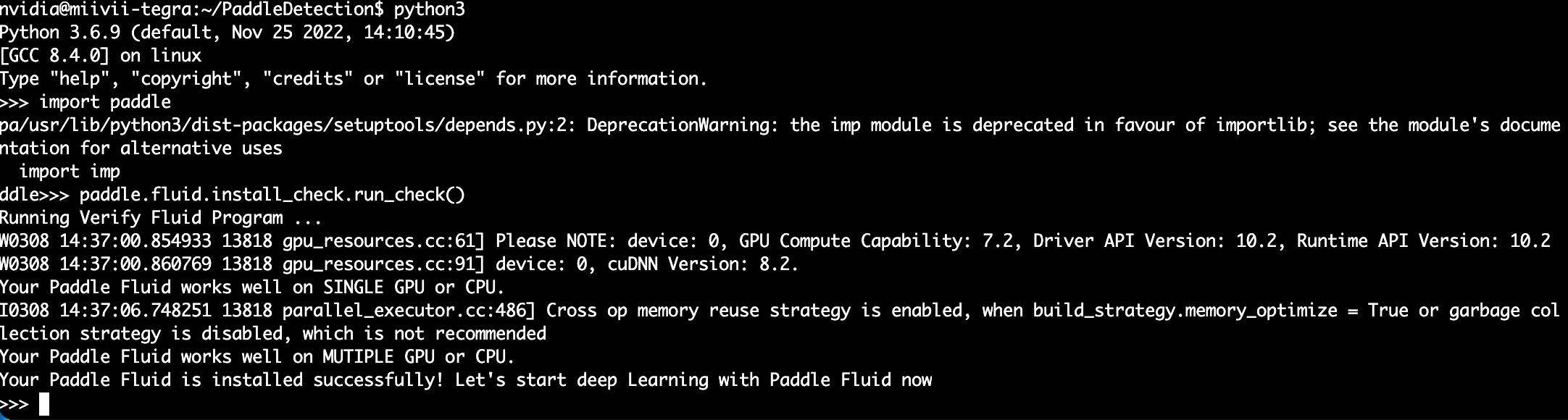
基于Jetson NX的模型部署
系统安装 系统安装过程分为3步: 下载必要的软件及镜像 Jetson Nano Developer Kit SD卡映像 https://developer.nvidia.com/jetson-nano-sd-card-image Windows版SD存储卡格式化程序 https://www.sdcard.org/downloads/formatter_4/eula_windows/ 镜像烧录工具…...
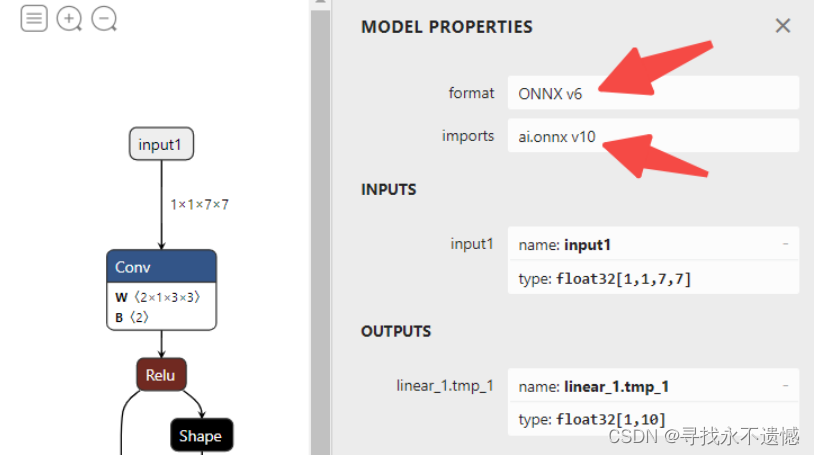
【PaddlePaddle onnx】PaddlePaddle导出ONNX及模型可视化教程
文章目录1 背景介绍2 实验环境3 paddle.onnx.export函数简介4 代码实操4.1 PaddlePaddle与ONNX模型导出4.2 ONNX正确性验证4.3 PaddlePaddle与ONNX的一致性检查4.4 多输入的情况5 ONNX模型可视化6 ir_version和opset_version修改7 致谢原文来自于地平线开发者社区,未…...

虹科案例 | 如何可持续的对变压器进行温度监控?
为了延长变压器的使用寿命,需要一个测量系统来监测内部整个绕组区域的温度。它必须明确温度升高发生的位置及其强度。您可以在此处了解为什么会这样以及如何在实践中实施? PART 1 变压器多点测温问题 变压器的工作温度越高,使用寿命越短。这里主要存在…...
Go之入门(特性、变量、常量、数据类型)
一、Go语言特性 语法简单并发性。Go语言引入了协程goroutine,实现了并发编程内存分配。Go语言为了解决高并发下内存的分配和管理,选择了tcmalloc进行内存分配(为了并发设计的高性能内存分配组件,使用cache为当前线程提供无锁分配…...
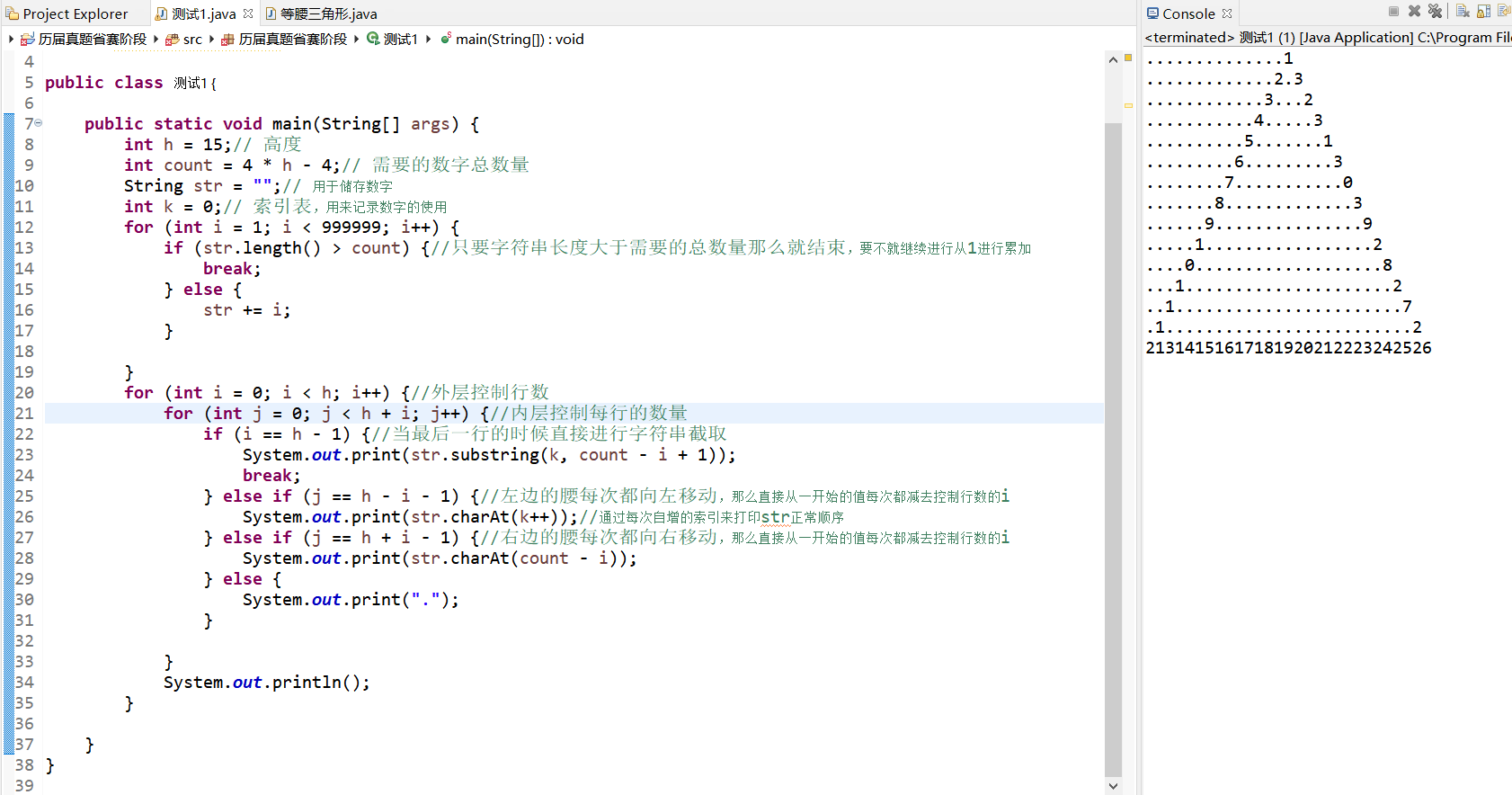
第九届省赛——8等腰三角形(找规律)
题目:本题目要求你在控制台输出一个由数字组成的等腰三角形。具体的步骤是:1. 先用1,2,3,...的自然数拼一个足够长的串2. 用这个串填充三角形的三条边。从上方顶点开始,逆时针填充。比如,当三角形高度是8时:…...

【产品设计】ToB 增删改查显算传
入职培训时技术leader说:“我不需要你们太聪明,做好基础的增删改查就可以了。”看似很简单的活,要做好并不容易。基础的坑在哪里呢? 一、 增(新增、创建、导入) 1. 明确表字段类型 新增的业务是由不同类型…...
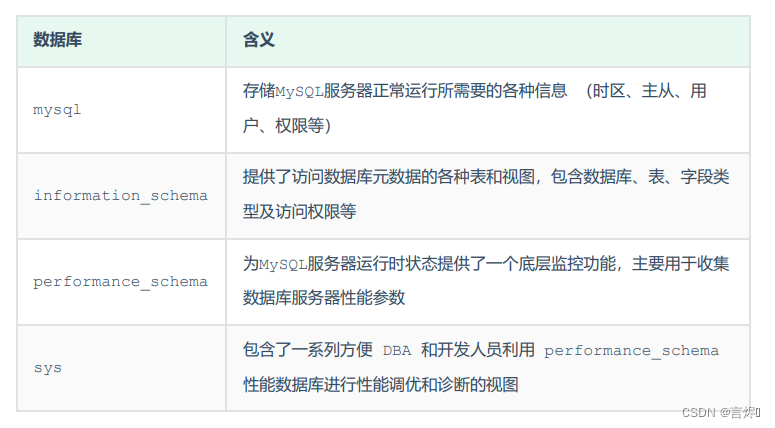
MySQL(二)视图、锁、存储过程、触发器、锁以及常用工具
MySQL进阶视图检查选项视图的更新存储过程存储过程基本语法变量系统变量用户自定义变量局部变量if判断参数casewhile循环repeat循环loop循环cursor游标handler条件处理程序存储函数触发器锁全局锁表级锁表锁元数据锁意向锁行级锁行锁间隙锁&临键锁InnoDB引擎逻辑存储结构事…...

CorelDRAW Graphics Suite2023更新内容介绍
懂设计的职场人都知道这款软件,CorelDRAW是一款非常高效的矢量图形设计软件。CorelDRAW操作界面简洁易懂,能够为用户提供精确地创建物体的尺寸和位置的功能,减少点击步骤,提高设计效率,节省设计时间。功能比普通的美图…...
 T1变幻)
2021牛客OI赛前集训营-提高组(第三场) T1变幻
2021牛客OI赛前集训营-提高组(第三场) 题目大意 对于一个大小为nnn的数组aaa的任意一点iii,若满足ai−1>aia_{i-1}>a_iai−1>ai且ai<ai1a_i<a_{i1}ai<ai1,则称iii为山谷点。111和nnn不可能为山谷点。…...

你还在使用if-else写代码吗,今天带你领略下策略模式的魅力!
1、什么是策略模式 策略模式其实也是在解耦,把策略的定义、创建、使用这三个部分解耦开来,因为本身策略模式也是基于接口编程,这样其实可以简单的理解客户端调用使用接口进行编程,可以通过工厂方法创建对应的策略模式,…...
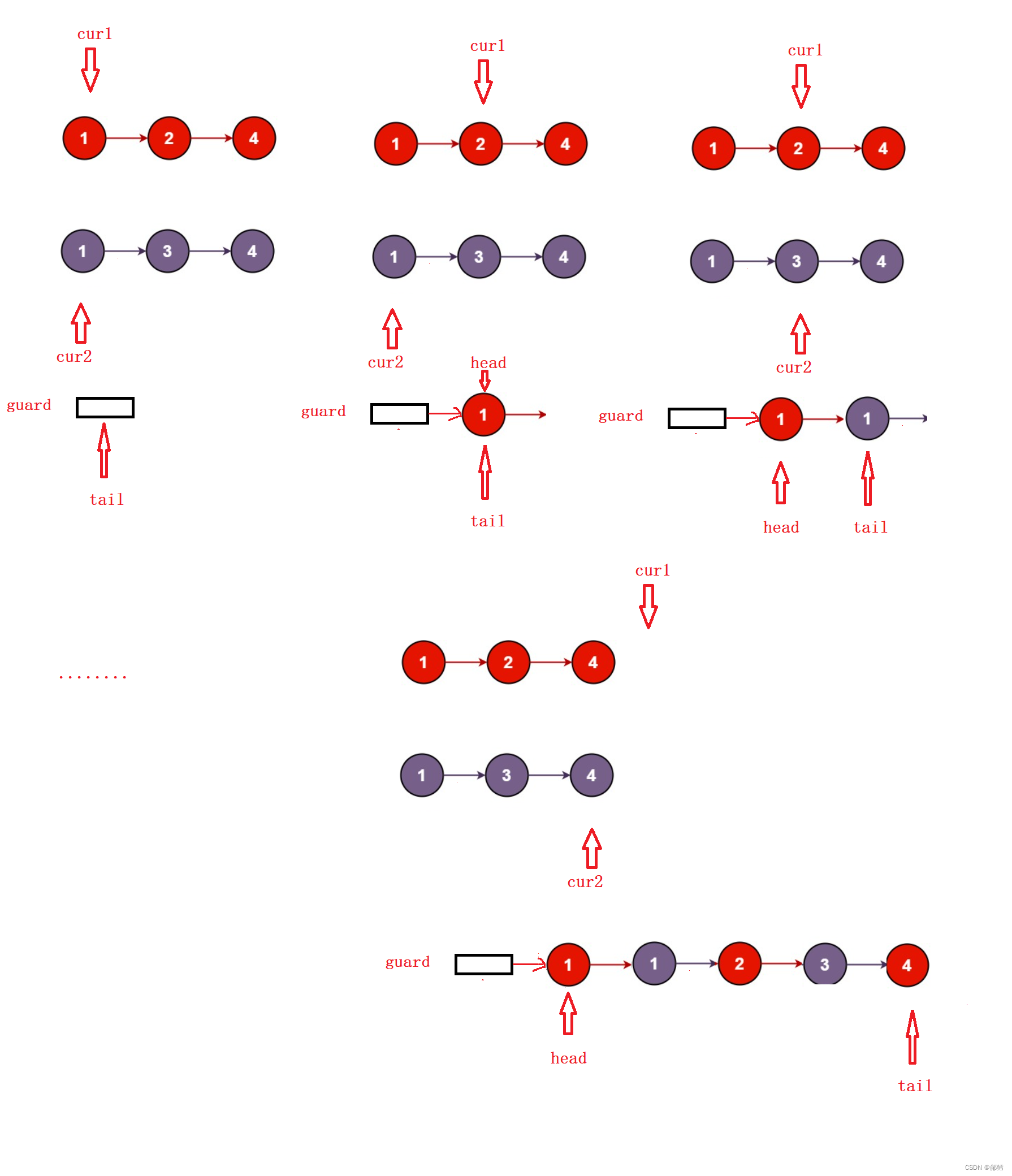
Leetcode. 21 合并两个有序列表
尾插 核心思路:依次比较 ,取经过比较后较小值进行尾插 cur1 指向list1 ,cur 2指向list2 ,当cur1走完list1 或者cur2 走完list2 后停止 如果cur1走完list1 ,可以将cur2 整个拿下来尾插 如果cur2走完list2 ,可以将cur1 整个拿下来尾插 特殊情况 ࿱…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
