【二叉树】Leetcode N 叉树的层序遍历
题目讲解
429. N 叉树的层序遍历
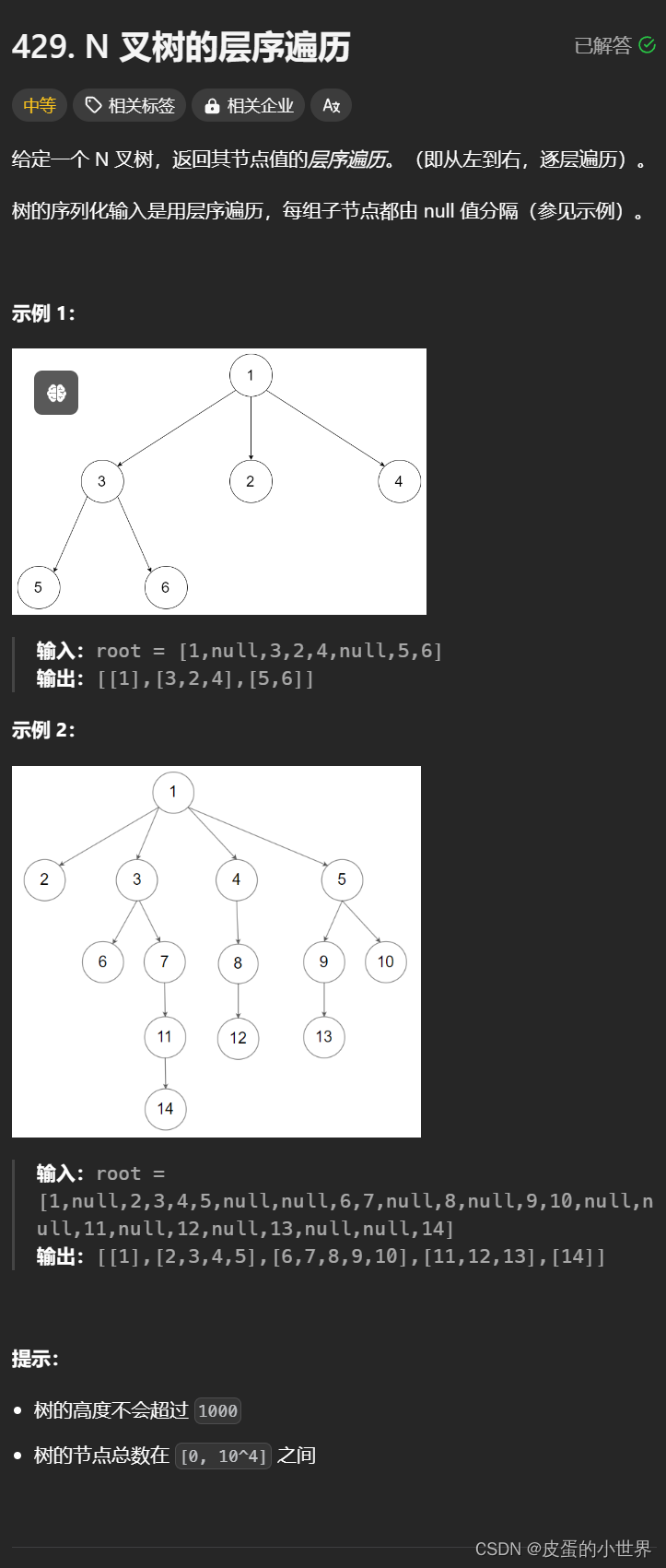
算法讲解
在做层序遍历的时候由于它的每一个结点是有val + vector child组成,所以在做层序遍历的时候需要考虑它每一层结点的个数,那我们就可以使用一个queue保存每一层的结点;那么我们在做第一层的时候,这样很简单,第一层用完怎么做呢?我们在准备第二层结点的时候,就需要将第一层结点提取出来,然后将第一层节点pop出去,现在的时候,第一层的vector ret已经出现的,但是我们queue还是没有处理的,所以在添加当前节点的val之后就需要遍历结点的child vector,将它的下一层结点放到queue中,这样的话,每一层的结点就会出现在queue中
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<vector<int>> levelOrder(Node* root) {int levesize = 0;queue<Node*>q;vector<vector<int>>ret;if(root == nullptr)return ret;q.push(root);while(!q.empty()){levesize = q.size();vector<int> temp;for(int i = 0; i < levesize; i++){Node* cur = q.front();q.pop();temp.push_back(cur->val);for(Node* child : cur->children){q.push(child);}}ret.push_back(temp);}return ret;}
};
相关文章:

【二叉树】Leetcode N 叉树的层序遍历
题目讲解 429. N 叉树的层序遍历 算法讲解 在做层序遍历的时候由于它的每一个结点是有val vector child组成,所以在做层序遍历的时候需要考虑它每一层结点的个数,那我们就可以使用一个queue保存每一层的结点;那么我们在做第一层的时候&am…...

Spring AI
目录 一、Spring AI 1、Spring AI简介 1.1、四次工业革命发展和变革 1.2、什么是人工智能? 1.3、人工智能的发展历程 1.4、什么是大模型? 1.5、如何训练大模型? 一、Spring AI 1、Spring AI简介 Spring AI Java接入人工智能大模型 1.1、四次工业革命发展和变革 人类…...

fiori SAP ui5 动态改变控件颜色
使用CustomData动态改变控件颜色 有时候我们需要改变控件颜色,对于高度封装的控件,显然改变控件CSS是比较困难的,幸好SAP UI5预设了一个customData的属性,每个控件都能使用她。 如下代码是判断汇率是否有改变,如果改…...

RabbitMQ php amqp
Linux debian 安装 Windows php amqp 扩展 PECL :: Package :: amqp 将 php_amqp.dll 复制到 php 的 ext 目录下 将 rabbitmq.4.dll 复制到 c:\windows\system32 目录下 php.ini extensionamqp...
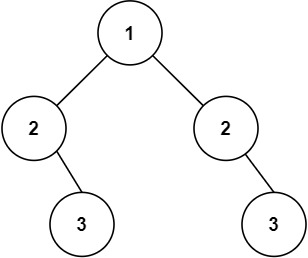
对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true示例 2: 输入:root [1,2,2,null,3,null,3] 输出:falses 思路:我刚开始是想着用…...

浅浅总结SQL中的事务.
在现实生活中有很多的线上支付的场景,当支付的时候,一方资金减少,另一方资金增加,在执行前后,两者的总体数额需要相同,为了保证这个操作的完整,所以提出了事务,那我们先来去写一个示例ÿ…...

C++ | Leetcode C++题解之第76题最小覆盖子串
题目: 题解: class Solution { public:unordered_map <char, int> ori, cnt;bool check() {for (const auto &p: ori) {if (cnt[p.first] < p.second) {return false;}}return true;}string minWindow(string s, string t) {for (const au…...

什么可以替代iframe?
网页嵌套中,iframe曾几何时不可一世,没有其他更好的选择! iframe即内联框架,作为网页设计中的一种技术,允许在一个网页内部嵌套另一个独立的HTML文档。尽管它在某些场景下提供了便利,但也存在多方面的缺陷…...

HTTP/1.0、HTTP/1.1、HTTP/2.0区别
文章目录 区别HTTP/1.0HTTP/1.11. 持久连接(长连接)2. 管道化3. Host头字段4. 分块传输编码5. 缓存机制6. 请求方法 HTTP/2.01. 二进制分帧2. 多路复用3. 服务器推送4. 优先级设置5. 头信息压缩6. 安全性7. 流量控制 区别 特性HTTP/1.0HTTP/1.1HTTP/2.0…...

鸿蒙内核源码分析(文件句柄篇) | 你为什么叫句柄
句柄 | handle int open(const char* pathname,int flags); ssize_t read(int fd, void *buf, size_t count); ssize_t write(int fd, const void *buf, size_t count); int close(int fd);只要写过应用程序代码操作过文件不会陌生这几个函数,文件操作的几个关键步骤嘛,跟把大…...
2024.5.8 关于 SpringCloud —— Ribbon 的基本认知
目录 Ribbon 负载均衡原理 工作流程 Ribbon 负载均衡规则 Ribbon 负载均衡自定义化 代码方式修改规则 配置文件方式修改规则 小总结 Ribbon 设定饥饿加载 Ribbon 负载均衡原理 工作流程 order-service 使用 RestTemplate 发送请求,随后该请求将会被 Ribbon 所…...

Lua 协程模拟 Golang 的 go defer 编程模式
封装go函数用于创建并启动一个协程: ---go函数创建并启动一个协程 ---param _co_task function 函数原型 fun(_co:thread) function go(_co_task)local co coroutine.create(_co_task) -- 创建一个暂停的协程coroutine.resume(co, co) -- 调用coroutine.resume激活…...
maven的安装与配置(超详细)
在Java开发中,配置Maven环境有几个重要的原因: 依赖管理:Maven 是一个强大的依赖管理工具,它能够帮助开发人员轻松地管理项目所需的各种第三方库和组件。通过在项目的 Maven 配置文件(pom.xml)中定义依赖&…...

springCloud服务降级使用到的组件
服务降级在Spring Cloud中通常使用的组件包括断路器(Circuit Breaker)和降级处理器(Fallback)。以下是它们的概念表述: 断路器(Circuit Breaker):断路器是一种设计模式,…...

Spring框架学习-详细
文章目录 1. Spring简介1.1 面向接口编程1.2 Spring简介1.3 Spring体系结构 2 Spring IoC - 基于XML2.1 Sping框架部署(IoC)2.2 Spring IoC使用2.3 IoC和DI2.4 DI依赖注入Spring容器通过反射方法实现属性注入有三种方式1. set方法注入2. 构造器注入 2.5 …...
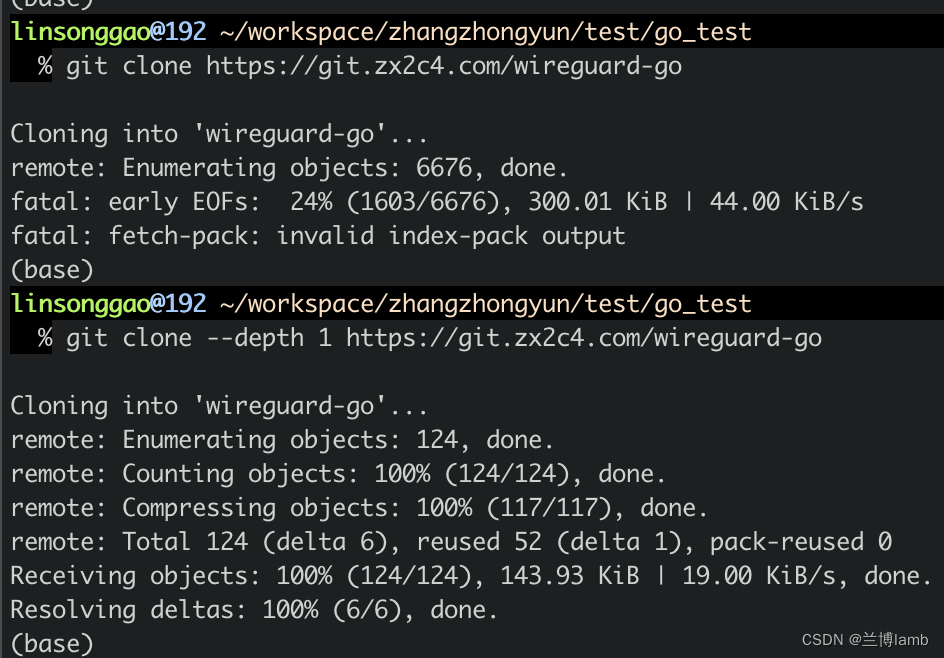
fatal: fetch-pack: invalid index-pack output
解决方案:git clone --depth1 要克隆的git地址 下载最近一次提交的代码 其他分支的内容都不下载 这样整体下载体量就变小了 执行命令:git clone --depth 1 https://gitlab.scm321.com/ufx/xxxx.git...

相机购买指南
佳能1000D 上市时间:2008年6月 简介: 佳能1000D具有1010万有效像素和7点宽区域自动对焦系统。DIGIC III影像处理器的应用使高ISO画质得到提升。小巧的机身和优质的成像质量可以满足初级用户对旅游便携与高画质的要求。使用了DIGIC III影像处理器&#x…...
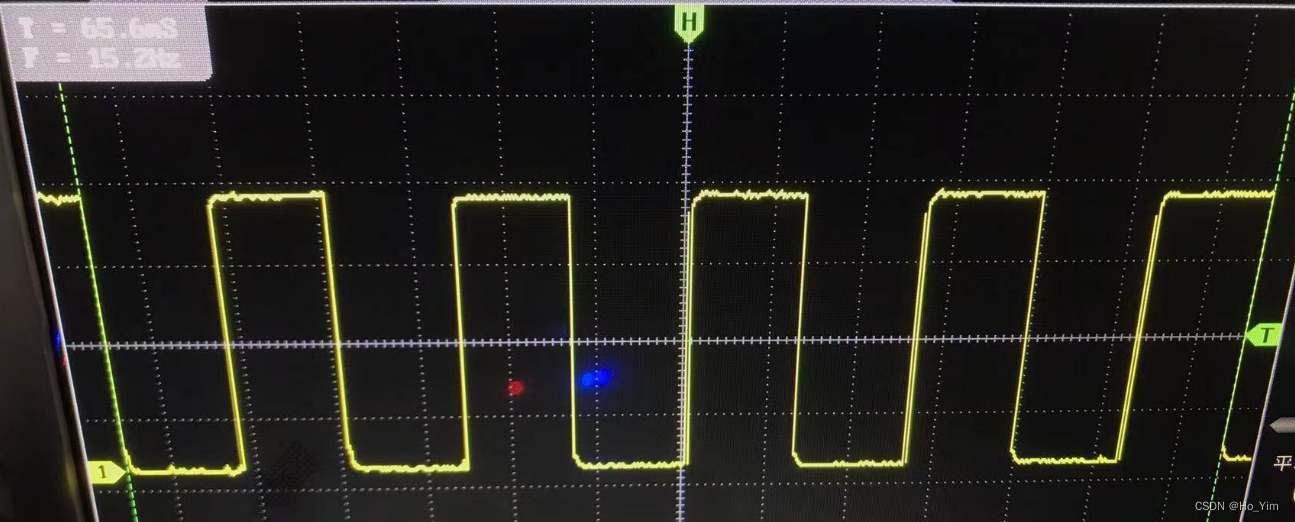
STM32微秒级别延时--F407--TIM1
基本配置: TIM1挂载在APB2总线上,150MHz经过15分频,得到10MHz计数频率,由于disable了自动重装载,所以只需要看下一次计数值是多少即可。 void TIM1_Delay_us(uint16_t us) //使用阻塞方式进行延时,ARR值不…...

AI图书推荐:杀手级ChatGPT提示词——利用人工智能实现成功与盈利
《杀手级ChatGPT提示词——利用人工智能实现成功与盈利》(Killer ChatGPT Prompts_ Harness the Power of AI for Success and Profit )一书是作者Guy Hart-Davis关于ChatGPT的指南,ChatGPT是OpenAI开发的大语言模型。这本书提供了各种职业角…...

AI时代:低代码与人工智能引领科技创造新时代
随着科技的飞速发展,我们步入了一个崭新的时代——AI时代。在这个时代,低代码和人工智能技术如日中天,成为引领科技创造的新引擎。本文将围绕这一主题,探讨低代码和人工智能如何在各个领域发挥巨大作用,推动科技创造迈…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
