凸优化理论学习一|最优化及凸集的基本概念
文章目录
- 一、优化问题
- (一)数学优化
- (二)凸优化
- 二、凸集
- (一)一些标准凸集
- (二)保留凸性的运算
- (三)正常锥和广义不等式
- (四)分离和支撑超平面
一、优化问题
(一)数学优化
从本质上讲,人工智能的目标就是最优化——在复杂环境中与多体交互中做出最优决策。几乎所有的人工智能问题都会归结为一个优化问题。
- 优化目标:minimize f 0 ( x ) f_0(x) f0(x)
- 约束条件:
- 非等式约束: f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq0,i=1,...,m fi(x)≤0,i=1,...,m
- 等式约束: g i ( x ) = 0 , i = 1 , . . . , m g_i(x)=0,i=1,...,m gi(x)=0,i=1,...,m
将最优化问题用于求解最佳决策时, x x x代表决策,约束用于限制决策或对结果施加条件
将最优化问题用于求解最优模型时, x x x 表示模型中的参数,约束对模型参数提出要求(例如,非负性)
最优化问题一般情况下不能得到完全的解决,但是可以尝试近似地解决它,而且通常无伤大雅。这个问题的例外情况是:凸优化问题。
一般非凸问题的传统技术通常会涉及到一定的妥协:
- 局部优化方法(非线性规划)
- 在其附近的可行点中找到一个使 f 0 f_0 f0 最小的点
- 可以处理大问题,例如神经网络训练
- 需要初始猜测,并且通常需要算法参数微调
- 不提供有关找到的点有多次优的信息
- 全局优化方法
- 找到(全局)解决方案
- 最坏情况的复杂性随着问题的规模呈指数级增长
- 通常基于解决凸子问题
(二)凸优化
凸优化问题是特殊形式的优化问题,包括线性规划 (LP)、二次规划 (QP) 等,我们通常能够可靠、高效地解决这些问题。
- 优化目标:minimize f 0 ( x ) f_0(x) f0(x)
- 约束条件:
- 非等式约束: f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq0,i=1,...,m fi(x)≤0,i=1,...,m
- 等式约束: A x = b Ax=b Ax=b
凸优化问题与最优化问题的对比:
- 凸优化问题的等式约束是线性的
- f 0 , . . . , f m f_0,..., f_m f0,...,fm是凸的: θ ∈ [ 0 , 1 ] , f i ( θ x + ( 1 − θ ) y ) ≤ θ f i ( x ) + ( 1 − θ ) f i ( y ) \theta \in [0,1],f_i(\theta x+(1-\theta)y)\leq\theta f_i(x)+(1-\theta)f_i(y) θ∈[0,1],fi(θx+(1−θ)y)≤θfi(x)+(1−θ)fi(y)
二、凸集
(一)一些标准凸集
仿射集包含通过集合中任意两个不同点的线(通过 x 1 x_1 x1、 x 2 x_2 x2两点的线: x = θ x 1 + ( 1 − θ ) x 2 , θ ∈ R x=\theta x_1+(1-\theta)x_2,\theta \in R x=θx1+(1−θ)x2,θ∈R)
- 函数形式为f=Ax+b,则称函数是仿射的,即线性函数加常数的形式。
- 比如线性方程组的解 { x ∣ A x = b } \{x |Ax = b\} {x∣Ax=b},并且每个仿射集都可以表示为线性方程组的解集

凸集包含集合中任意两点之间的线段( x 1 x_1 x1和 x 2 x_2 x2两点间的线段: x = θ x 1 + ( 1 − θ ) x 2 , 0 ≤ θ ≤ 1 x=\theta x_1+(1-\theta)x_2,0\leq\theta\leq1 x=θx1+(1−θ)x2,0≤θ≤1)
- 凸集满足对于 x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 x_1,x_2\in C,0\leq\theta\leq1 x1,x2∈C,0≤θ≤1,有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+(1-\theta)x_2\in C θx1+(1−θ)x2∈C;
- 以下为一个凸集和两个非凸集的示意:

为什么 x = θ x 1 + ( 1 − θ ) x 2 x=\theta x_1+(1-\theta)x_2 x=θx1+(1−θ)x2可以表示任意两点连接线段的所有点?将上式展开得:
x = θ x 1 + ( 1 − θ ) x 2 = θ x 1 + x 2 − θ x 2 = θ ( x 1 − x 2 ) + x 2 x=\theta x_1+(1-\theta)x_2=\theta x_1+x_2-\theta x_2=\theta(x_1-x_2)+x_2 x=θx1+(1−θ)x2=θx1+x2−θx2=θ(x1−x2)+x2
凸包: S 中所有点的凸组合的集合( x 1 , . . . , x k x_1,...,x_k x1,...,xk的凸组合: x = θ 1 x 1 + θ 2 x 2 + . . . + θ k x k x=\theta_1 x_1+\theta_2 x_2+...+\theta_k x_k x=θ1x1+θ2x2+...+θkxk,其中 θ 1 + . . . + θ k = 1 , θ i ≥ 0 \theta_1+...+\theta_k =1,\theta_i \geq 0 θ1+...+θk=1,θi≥0)

凸锥体: 包含集合中点的所有圆锥组合的集合( x 1 x_1 x1和 x 2 x_2 x2的圆锥组合: x = θ 1 x 1 + θ 2 x 2 x=\theta_1 x_1+\theta_2 x_2 x=θ1x1+θ2x2,且 θ 1 ≥ 0 , θ 2 ≥ 0 \theta_1\geq0,\theta_2\geq0 θ1≥0,θ2≥0)

超平面: 形式为 { x ∣ a T x = b } \{x | a^T x = b\} {x∣aTx=b}的集合,其中 a ≠ 0 a ≠ 0 a=0,半空间: 形式为 { x ∣ a T x ≤ b } \{x | a^T x \leq b\} {x∣aTx≤b}的集合,其中 a ≠ 0 a ≠ 0 a=0。(a是法向量,超平面是仿射和凸的;半空间是凸的)

欧几里得球: B ( x c , r ) = { x ∣ ∣ ∣ x − x c ∣ ∣ 2 ≤ r } = { x c + r u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } B(x_c,r)=\{x|\ ||x-x_c||_2\leq r\} = \{x_c+ru|\ ||u||_2\leq1\} B(xc,r)={x∣ ∣∣x−xc∣∣2≤r}={xc+ru∣ ∣∣u∣∣2≤1}
椭球: { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } = { x c + r u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } = { x c + A u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } \{x|\ (x-x_c)^T P^{-1}(x-x_c)\leq 1\} = \{x_c+ru|\ ||u||_2\leq1\} = \{x_c+Au|\ ||u||_2\leq1\} {x∣ (x−xc)TP−1(x−xc)≤1}={xc+ru∣ ∣∣u∣∣2≤1}={xc+Au∣ ∣∣u∣∣2≤1},其中 P ∈ S + + n P\in S^n_{++} P∈S++n,也就是说P 对称正定,A平方且非奇异。
中心为 x c x_c xc,半径为 r r r 的标准球: { x ∣ ∣ ∣ x − x c ∣ ∣ ≤ r } \{x|\ ||x − x_c|| ≤ r\} {x∣ ∣∣x−xc∣∣≤r}
标准锥: { ( x , t ) ∣ ∣ ∣ x ∣ ∣ ≤ t } \{(x, t) |\ ||x||≤t\} {(x,t)∣ ∣∣x∣∣≤t}
欧几里得范数锥: { ( x , t ) ∣ ∣ ∣ x ∣ ∣ 2 ≤ t } \{(x, t) |\ ||x||_2≤t\} {(x,t)∣ ∣∣x∣∣2≤t}
多面体 是有限多个线性不等式和等式的解集,也是有限数量的半空间和超平面的交集。 { x ∣ A x ≤ b , C x = d } \{x| Ax\leq b,Cx=d\} {x∣Ax≤b,Cx=d}
(二)保留凸性的运算
证明集合 C 凸性的方法:
- 基于定义:如果 x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 x_1,x_2\in C,0\leq\theta\leq 1 x1,x2∈C,0≤θ≤1,则有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+(1-\theta)x_2\in C θx1+(1−θ)x2∈C;
- 使用凸函数;
- 表明 C 是通过保留凸性的操作从简单凸集(超平面、半空间、范数球……)获得的;
交运算:(任意数量的)凸集的交集是凸的。

仿射映射:凸集的仿射映射也是凸的。(函数形式为f=Ax+b,则称函数是仿射的,即线性函数加常数的形式。)
 (仿射变换就认为是一个矩阵变换,足球可以映射成一个橄榄球,依然是凸集。)
(仿射变换就认为是一个矩阵变换,足球可以映射成一个橄榄球,依然是凸集。)
由仿射变换推出凸集的和也是凸集:

透视函数:凸集在透视下的像和逆像都是凸的(透视函数实际上就是对向量进行伸缩规范化)

线性分数函数是仿射映射函数和透视变换的复合函数,依然还是保凸运算,凸集在线性分数函数下的像和逆像都是凸的。从联合概率到条件概率的变换是一个线性分数函数。

(三)正常锥和广义不等式
正常锥的定义:如果凸锥体 K ⊆ R n K⊆R_n K⊆Rn满足如下条件,则称锥 K ⊆ R n K⊆R_n K⊆Rn为正常锥。
- K是凸的
- K是闭的
- K是实的,即K有非空的内部
- K是尖的,即K不包含任何直线

广义不等式满足类似普通不等式的性质,如传递性,反对称性等等。 广义不等式和普通不等式最大的区别是不是任意两点都是可比的。即 x ≤ y x≤y x≤y 和 y ≤ x y≤x y≤x对于普通不等式二者必居其一。而对于广义不等式这不一定成立。所以最小,最大这些概念对于广义不等式变得很复杂。
(四)分离和支撑超平面
分离超平面:利用超平面将两个不相交的凸集分离开来,即得到超平面分离定理。


支撑超平面:如果C是凸的,那么在C的每个边界点都存在一个支持超平面。

 支撑超平面不完全逆定理:如果一个集合是闭的,具有非空内部并且其边界上每个点均存在支撑超平面,那么它是凸的。
支撑超平面不完全逆定理:如果一个集合是闭的,具有非空内部并且其边界上每个点均存在支撑超平面,那么它是凸的。
参考:
凸优化之保凸运算
广义不等式
【最优化理论与算法】数学预备知识、凸集和凸函数
相关文章:

凸优化理论学习一|最优化及凸集的基本概念
文章目录 一、优化问题(一)数学优化(二)凸优化 二、凸集(一)一些标准凸集(二)保留凸性的运算(三)正常锥和广义不等式(四)分离和支撑超…...
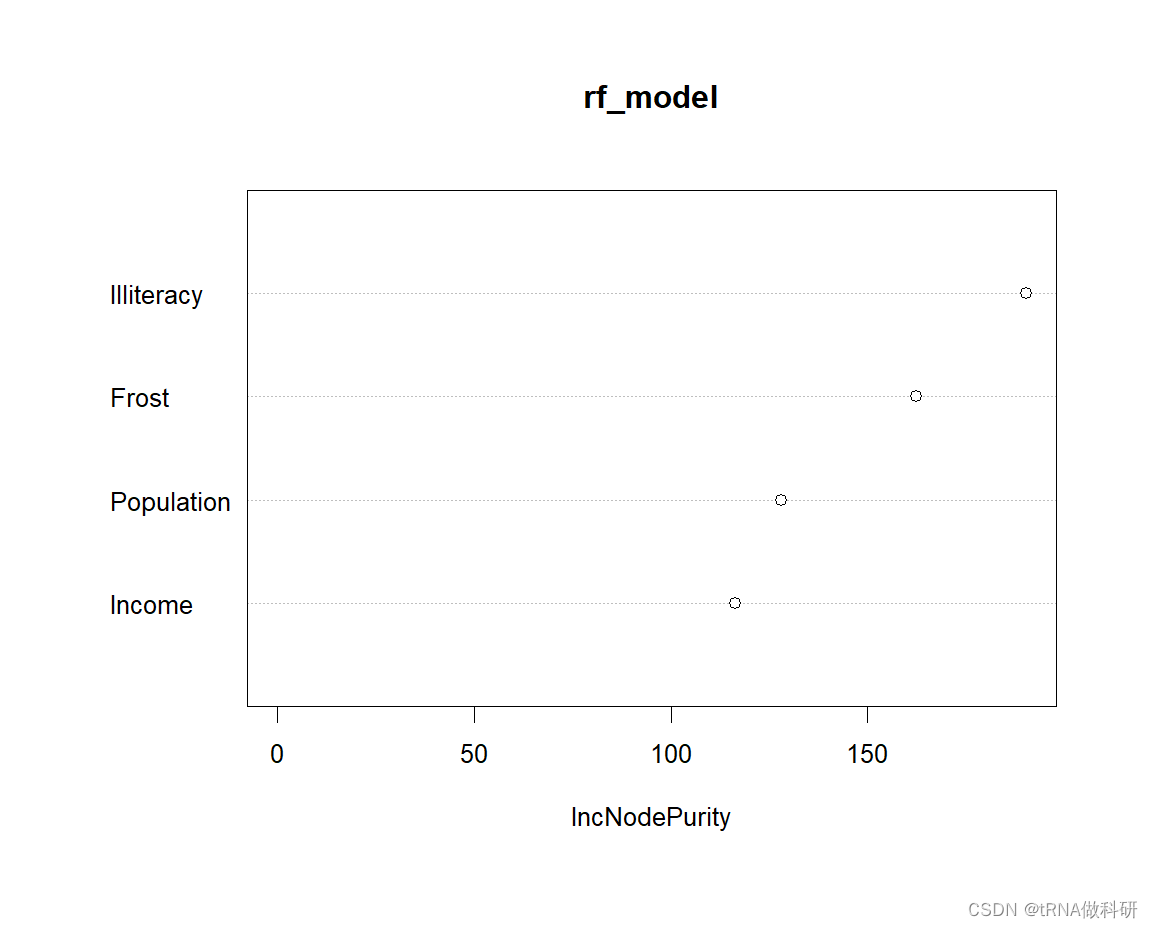
【R语言从0到精通】-4-回归建模
通过之前的文章,我们已经基本掌握了R语言的基本使用方法,那从本次教程开始,我们开始聚焦如何使用R语言进行回归建模。 4.1 回归简介 回归分析是一种统计学方法,用于研究两个或多个变量之间的相互关系和依赖程度。它可以帮助我们了…...
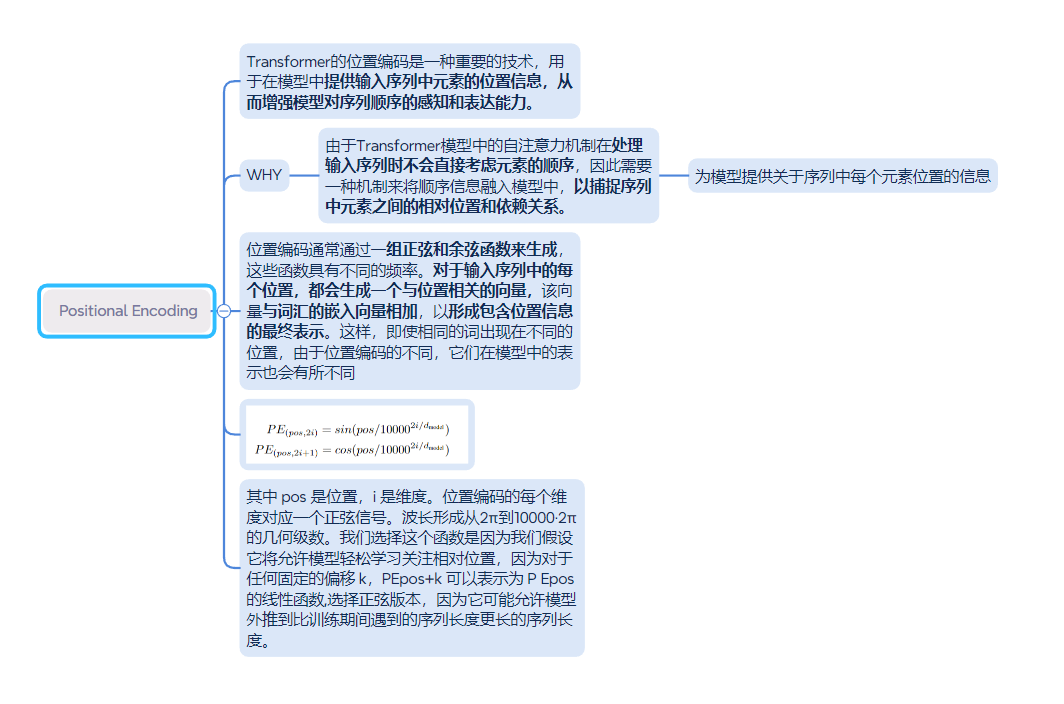
论文 学习 Transformer : Attention Is All You Need
目录 概述: 对摘要的理解: 框架解析 按比例缩放的点积注意力 多头注意力机制 前馈神经网络与位置编码 概述: transformer 是一个encoder ——decoder 结构的用于处理序列到序列转换任务的框架,是第一个完全依赖自注意力机制…...

工厂模式+策略模式
输入实体 基类 import lombok.Data;Data public class PersonInputDto {private Integer id;private String name; }子类 Data AllArgsConstructor NoArgsConstructor public class ManPerson extends PersonInputDto {private String sex; }Data AllArgsConstructor NoArgs…...
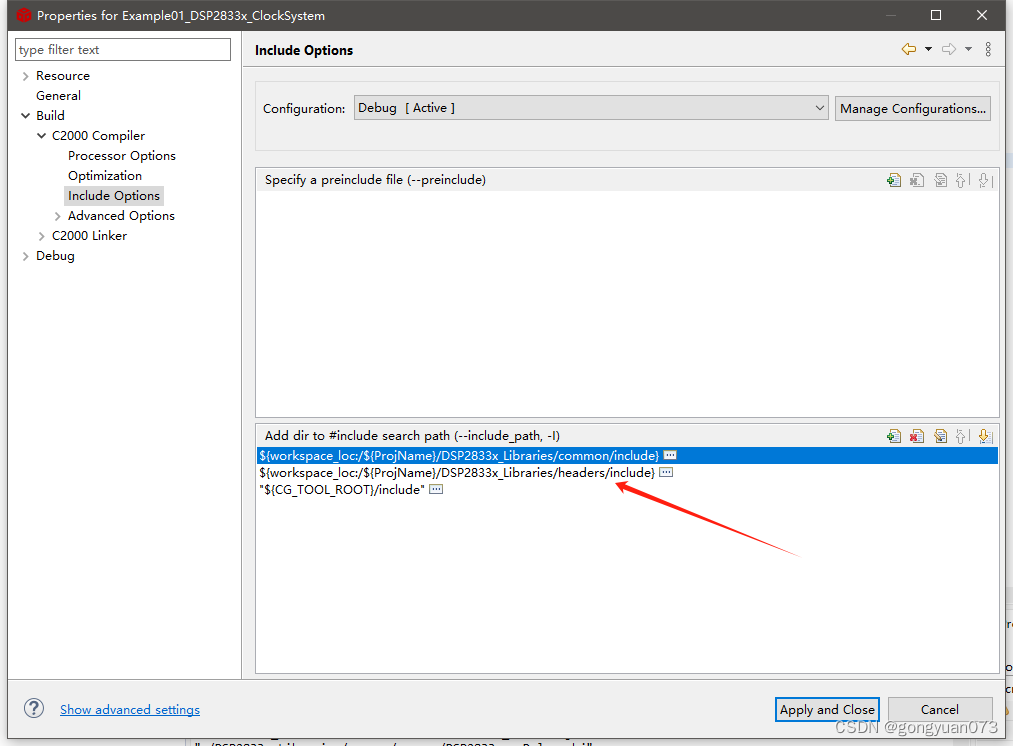
TMS320F28335学习笔记-时钟系统
第一次使用38225使用了普中的clocksystem例程进行编译,总是编译失败。 问题一:提示找不到文件 因为工程的头文件路径没有包含,下图的路径需要添加自己电脑的路径。 问题二 找不到库文件 例程种的header文件夹和common文件夹不知道从何而来…...

【Apache POI】Apache POI-操作Excel表格-简易版
Catalog Apache POI-操作Excel表格1. 需求2. 优点3. 缺点4. 应用场景5. 使用方法6. SpringBoot工程中处理Excel表格7. Demo示例 Apache POI-操作Excel表格 1. 需求 大多数项目的在运营过程中,会产生运营数据,如外卖系统中需要统计每日的订单完成数、每…...

MySQL系列之索引
🌹作者主页:青花锁 🌹简介:Java领域优质创作者🏆、Java微服务架构公号作者😄 🌹简历模板、学习资料、面试题库、技术互助 🌹文末获取联系方式 📝 往期热门专栏回顾 专栏…...

【问题分析】锁屏界面调起google语音助手后壁纸不可见【Android 14】
1 问题描述 为系统和锁屏分别设置两张不同的壁纸,然后在锁屏界面长按Power调起google语音助手后,有时候会出现壁纸不可见的情况,如以下截图所示: 有的时候又是正常的,但显示的也是系统壁纸,并非是锁屏壁纸…...
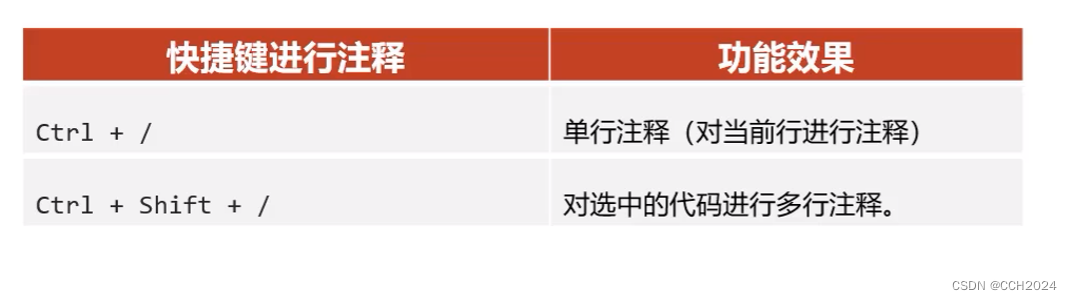
Java入门基础学习笔记8——注释
1、注释: 注释是写在程序中对代码进行解释说明的文件,方便自己和其他人查看,以便理解程序的。 package cn.ensource.note;/**文档注释文档注释 */ public class NoteDemo {public static void main(String[] args) {// 单行注释System.out.…...

上班工资太低了,哪些副业可以多赚钱?
今天给各位分享最赚钱的副业方式的知识,其中也会对比较赚钱的副业进行解释. 1、网站接单 一般20页左右的PPT报价基本在200-400元。如果能每周接单,一个月就有接近1000元的副业收入。提交摄影和绘画作品 比起画画,靠摄影赚点外快更容易一点。…...
原子学习笔记4——GPIO 应用编程
一、应用层如何操控 GPIO 与 LED 设备一样,GPIO 同样也是通过 sysfs 方式进行操控,进入到/sys/class/gpio 目录下,如下所示: gpiochipX:当前 SoC 所包含的 GPIO 控制器,我们知道 I.MX6UL/I.MX6ULL 一共包…...

查看iqn编码
cat /etc/iscsi/initiatorname.iscsi ## for each iSCSI initiator. Do NOT duplicate iSCSI InitiatorNames. InitiatorNameiqn.2004-10.com.ubuntu:01:9ebe1a68...
如何安全的使用密码登录账号(在不知道密码的情况下)
首先,需要用到的这个工具: 度娘网盘 提取码:qwu2 蓝奏云 提取码:2r1z 1、打开工具,进入账号密码模块,如图 2、看到鼠标移动到密码那一栏有提示,按住Ctrl或者Alt点击或者双击就能复制内容&…...

软件需求和设计评审
目录 引言 1. 软件评审的方法和技术 2. 产品需求评审:构建正确的产品 3. 设计评审:构建正确的产品 4. 软件评审的最佳实践 结语 引言 在软件开发的迷宫中,需求和设计评审是通往成功产品的关键门户。它们是确保软件质量和满足用户需求的…...
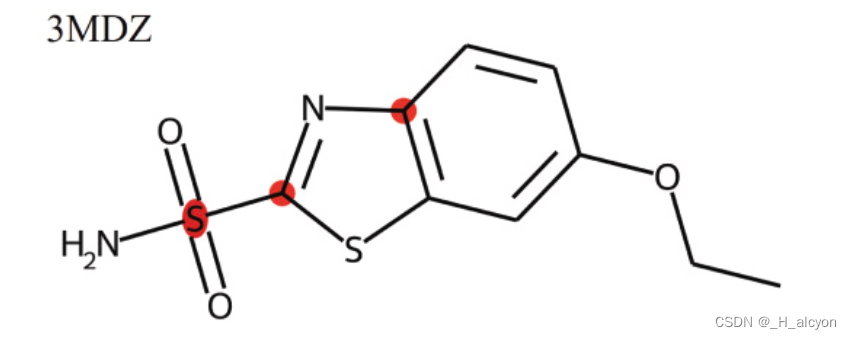
论文笔记ColdDTA:利用数据增强和基于注意力的特征融合进行药物靶标结合亲和力预测
ColdDTA发表在Computers in Biology and Medicine 的一篇一区文章 突出 • 数据增强和基于注意力的特征融合用于药物靶点结合亲和力预测。 • 与其他方法相比,它在 Davis、KIBA 和 BindingDB 数据集上显示出竞争性能。 • 可视化模型权重可以获得可解释的见解。 …...
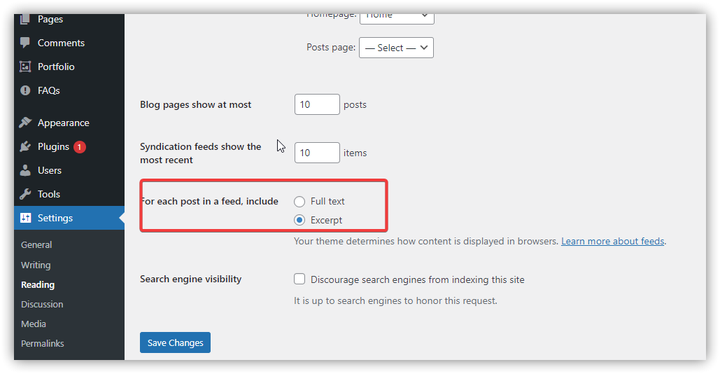
如何防止WordPress网站内容被抓取
最近在检查网站服务器的访问日志的时候,发现了大量来自同一个IP地址的的请求,用站长工具分析确认了我的网站内容确实是被他人的网站抓取了,我第一时间联系了对方网站的服务器提供商投诉了该网站,要求对方停止侵权行为,…...

全球化战略中的技术支柱:出海企业的网络技术解决方案
随着全球市场的一体化,中国的电商与游戏行业越来越倾向于扩展国际市场,这一过程被称为“出海”。成功的出海战略不仅需要强大的市场洞察和文化适应能力,还需依赖高效的网络技术,包括SOCKS5代理、代理IP、以及全面的网络安全策略。…...
在Linux上安装并运行RabbitMQ
目录 准备CentOS服务器 下载rabbit-server和erlang文件 启动RabbitMQ服务 准备CentOS服务器 两个命令,选一个能用的,查看CentOS服务器的版本 lsb_release -a下载rabbit-server和erlang文件 参考文章:http://t.csdnimg.cn/t8BbM 1、创建新…...
使用 docker-compose 搭建个人博客 Halo
说明 我这里使用的是 Halo 作为博客的工具,毕竟是开源了,也是使用 Java 写的嘛,另外一点就是使用 docker 来安装(自动挡,不用自己考虑太多的环境因素),这样子搭建起来更快一点,我们…...

《这就是ChatGPT》读书笔记
书名:这就是ChatGPT 作者:[美] 斯蒂芬沃尔弗拉姆(Stephen Wolfram) ChatGPT在做什么? ChatGPT可以生成类似于人类书写的文本,它基本任务是弄清楚如何针对它得到的任何文本产生“合理的延续”。当ChatGPT写…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

