远程桌面如何连接?
远程桌面连接是一种可以在不同地点之间共享电脑桌面的技术。通过远程桌面连接,用户可以在远程的计算机上操作另一台计算机,就像是直接坐在前者的前面一样。这种技术可以帮助用户解决在不同地点之间共享数据、协同办公、设备管理等问题。

【天联】的使用场景
【天联】是一种远程桌面连接软件,它可以应用于各种场景:

-
结合医药、餐饮、商超等零售、收银软件应用实现异地统一管理。通过远程桌面连接,电脑上的零售、收银软件可以被远程操作,这样就可以实现异地的统一管理。比如,一家连锁药店可以通过远程桌面连接,将所有分店的收银系统连接在一起,实现数据的统一管理和及时更新。

-
结合OA、CRM、ERP、财务进销存等系统应用实现随时随地协同办公。远程桌面连接可以帮助公司员工在不同地点之间进行协同办公。不论员工身在何处,只要有网络连接,就可以通过远程桌面连接进入办公电脑并进行工作。这种方式提供了更大的灵活性,使得员工可以更好地协同工作、解决问题和提高工作效率。
-
结合视频监控设备和物联网设备应用,实现远程数据采集管理。远程桌面连接不仅可以用于操作电脑,还可以应用于远程操作和管理其他设备。比如,通过远程桌面连接,可以远程操作视频监控设备,在不同地点之间进行实时监控。也可以远程连接物联网设备,实现对其数据采集和管理的远程操作。
远程桌面连接技术的出现为各行各业的工作流程和数据管理提供了更大的便利。通过远程桌面连接,用户可以轻松地在不同地点之间共享桌面,实现数据的共享、协同办公和远程设备管理。【天联】作为一种远程桌面连接软件,广泛应用于各个领域,帮助用户解决了许多跨地域操作和管理的难题。在今后的发展中,我们可以期待远程桌面连接技术的进一步创新和应用。
相关文章:

远程桌面如何连接?
远程桌面连接是一种可以在不同地点之间共享电脑桌面的技术。通过远程桌面连接,用户可以在远程的计算机上操作另一台计算机,就像是直接坐在前者的前面一样。这种技术可以帮助用户解决在不同地点之间共享数据、协同办公、设备管理等问题。 【天联】的使用场…...
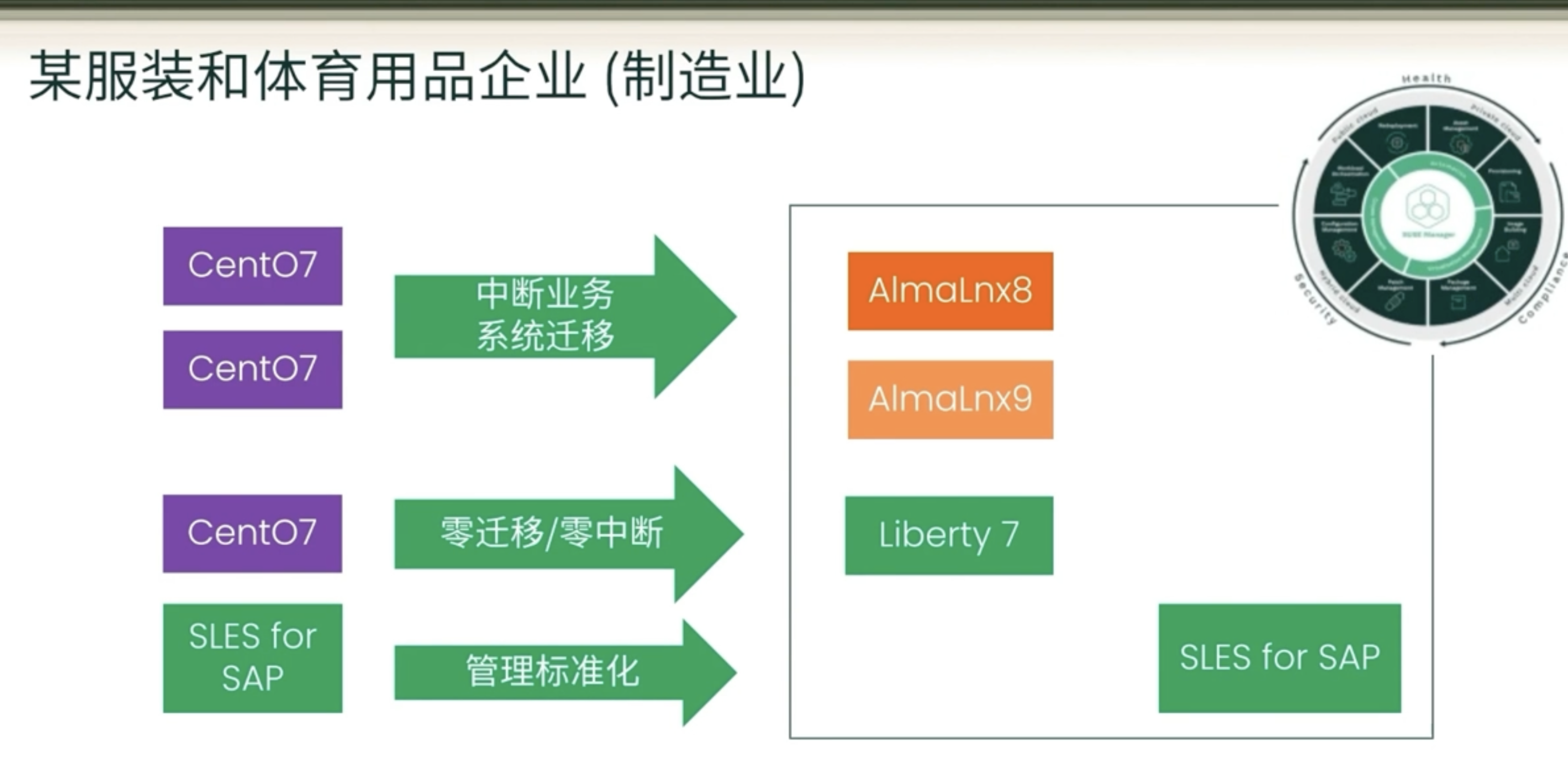
Centos 停服倒计时!你的操作系统何去何从?
在计算机技术的不断演进中,操作系统扮演着至关重要的角色。然而,对于许多企业和个人用户来说,CentOS的突然停服消息带来了一场不小的冲击。作为一款备受欢迎的企业级Linux发行版,CentOS的停服意味着用户需要重新评估自己的操作系统…...

ITMS-91053: Missing API declaration
1. 添加PrivacyInfo.xcprivacy File → New → File → App Privacy 2. 格式 3. 已知对应关系 NSPrivacyAccessedAPICategoryFileTimestamp 3B52.1: Files provided to app by user, per documentation:File Timestamp NSPrivacyAccessedAPICategoryDiskSpace …...

iOS 裁剪图片
参考资源 YSHYClipImageDemo YQImageTool 裁剪图片 完整demo:https://github.com/liquangang/cutImageFinish...

算法训练营第60天|LeetCode 647.回文子串 516.最长回文子序列
LeetCode 647.回文子串 题目链接: LeetCode 647.回文子串 代码: class Solution { public:int countSubstrings(string s) {int size s.size();int result 0;vector<vector<int>>dp(size,vector<int>(size,false));for(int i si…...
读天才与算法:人脑与AI的数学思维笔记25_涌现理论
1. 人工智能新闻 1.1. 人工智能新闻报道算法的核心是如何将未经处理的原始数据转换成新闻报道 1.2. 很少有记者为美联社决定使用机器来帮助报道这些新闻持反对意见 1.2.1. 像“Wordsmith”这样的算法,具有自动化的洞察力、科学的叙事能力,现在正被应用…...
)
C/C++ IPV6服务器socket绑定在::,接受ipv4链接(双栈)
先决条件: 1、 创建IPV6套接字 2、打开套接字可重用 3、禁用仅限 IPV6 BOOL bEnable FALSE; if (setsockopt(listenfd_, IPPROTO_IPV6, IPV6_V6ONLY, reinterpret_cast<char*>(&bEnable), sizeof(bEnable)) < 0) …...
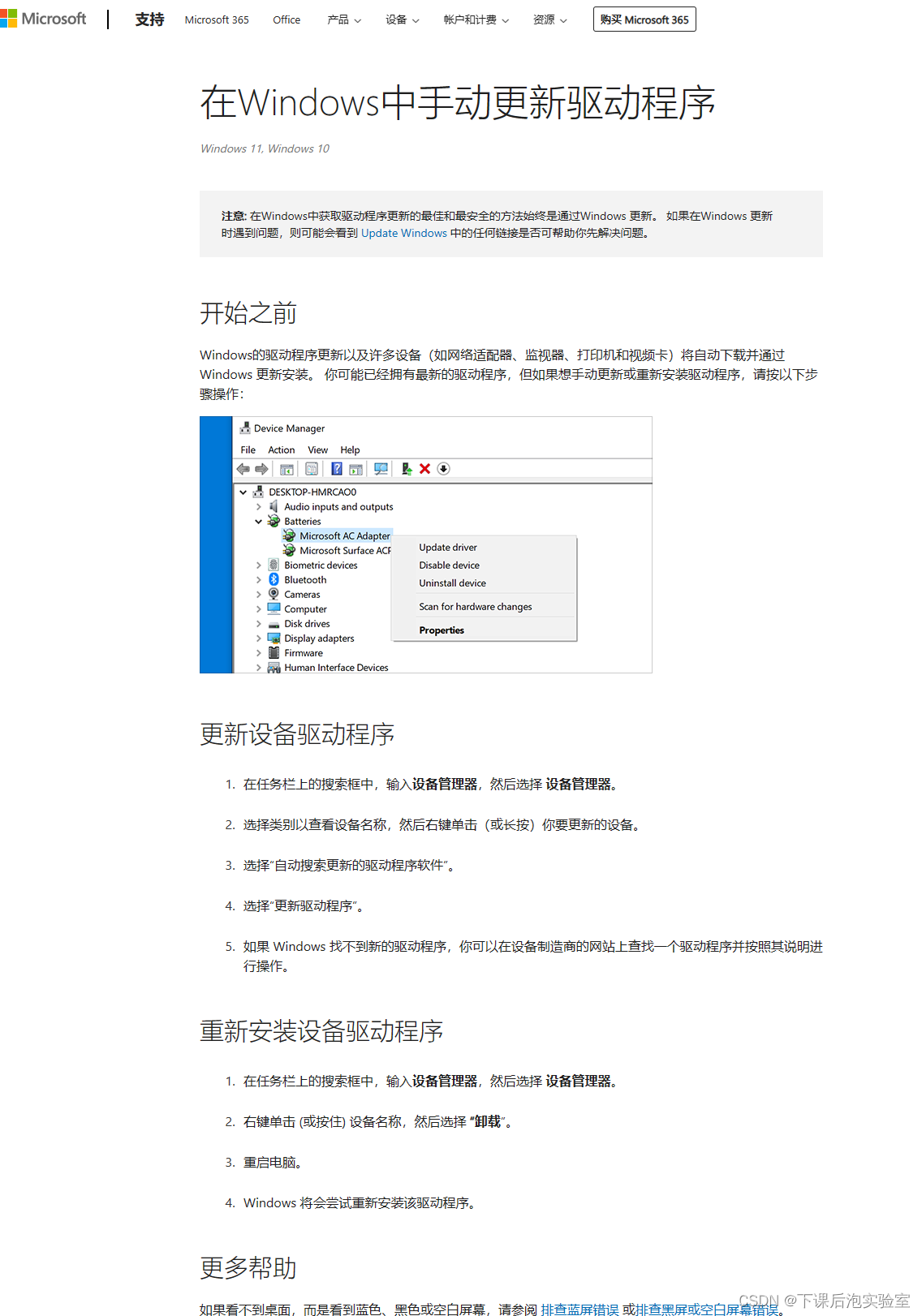
【Win10设备管理器中无端口选项】
计算机疑难杂症分享002 Win10设备管理器中无端口选项1、问题现象2、问题原因3、问题解决3.1、驱动精灵(亲测的此方法)3.2、添加过时硬件3.3、官方的方法 Win10设备管理器中无端口选项 1、问题现象 当我调试串口通信时,发现打开设备管理器没有端口,打开…...
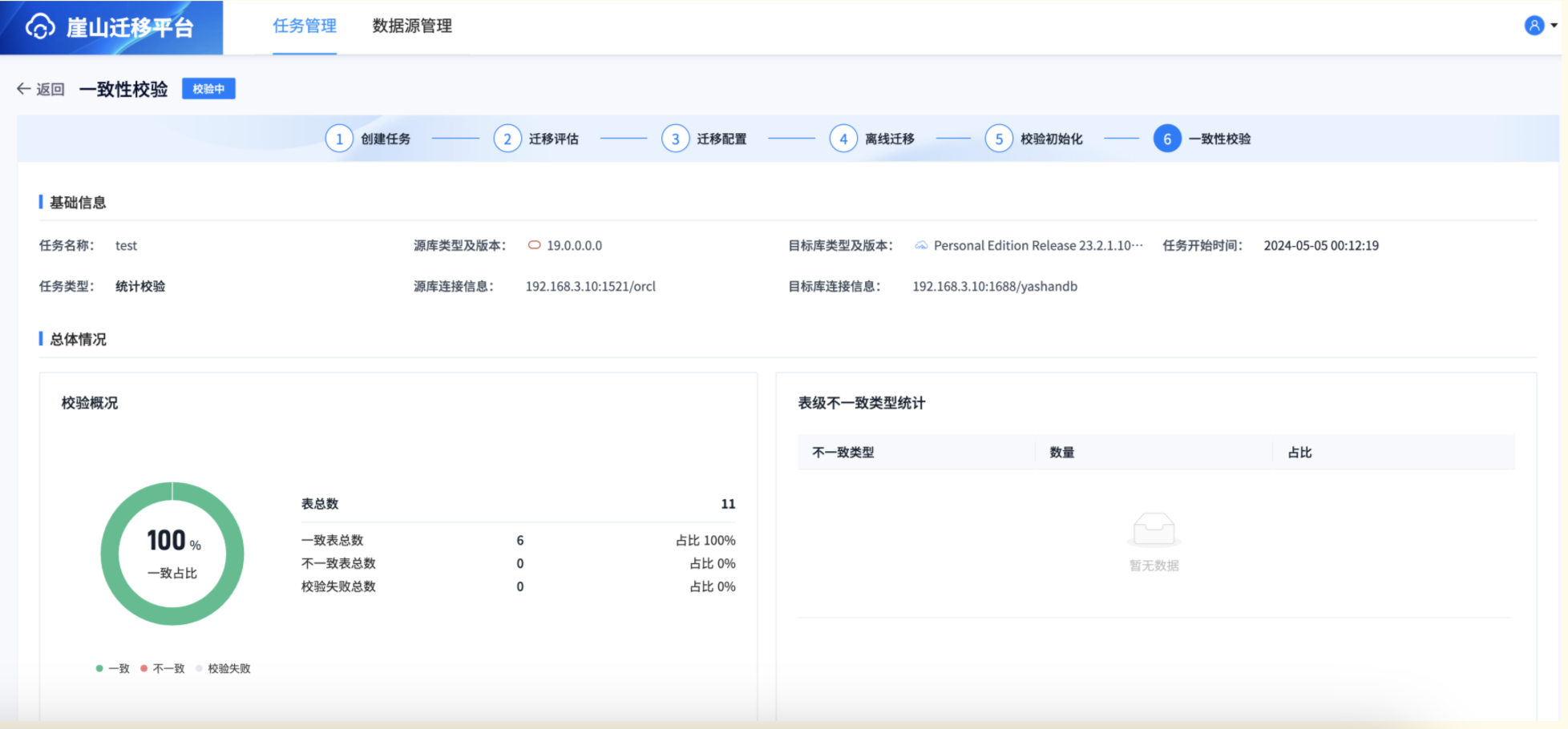
「YashanDB迁移体验官」Oracle向YashanDB迁移的丝滑体验
📢📢📢📣📣📣 作者:IT邦德 中国DBA联盟(ACDU)成员,10余年DBA工作经验, Oracle、PostgreSQL ACE CSDN博客专家及B站知名UP主,全网粉丝10万 擅长主流Oracle、My…...

实现用户个人随机salt生成jwt及鉴别用户权限的实现思路
实现用户个人随机salt生成jwt及鉴别用户权限的实现 盐值是什么? 盐值(salt)是在密码学中用于增加密码安全性的一种随机值。它通常是一个随机生成的字符串,与用户密码结合在一起,然后再进行加密处理。盐值的作用是增加…...

AI工具的热门与卓越:揭示AI技术的实际应用和影响
文章目录 每日一句正能量前言常用AI工具创新AI应用个人体验分享后记 每日一句正能量 我们在我们的劳动过程中学习思考,劳动的结果,我们认识了世界的奥妙,于是我们就真正来改变生活了。 前言 随着人工智能(AI)技术的快…...

VUE el-button指定图片背景
似乎只能通过css指定? 代码1 <el-button circleclass"stream0"click"switchToStream(0)" > </el-button> 代码2 <style>.stream0 {background-size: cover;background-image: url(~/assets/stream.png); } 如果要动态变…...

【ARM 嵌入式 C 入门及渐进 1.2 -- 是否为 n 字节对齐】
文章目录 是否为 n 字节对齐 是否为 n 字节对齐 在C语言中,你可以定义一个宏来检查一个给定地址是否是n字节对齐的。这里的n应该是2的幂(例如,2、4、8、16等)。要做到这一点,可以利用位操作的特性。具体地,…...

适配qnx和linux平台的线程管理类封装
概述 封装代码仓库: https://gitee.com/liudegui/my_thread 尝试封装一个基于C11的多线程控制与调度类,适配QNX和Linux平台,且代码符合Misra标准。它提供了以下主要功能: 线程的创建与销毁管理。线程的优先级调度。线程的CPU亲…...

【信息系统项目管理师】复习~第十五章
15.项目风险管理 每个项目都存在两个层面上的风险:①每个项目都有会影响项目达成目标的单个风险;②由单个风险和不确定性的其他来源联合导致的整体项目风险。项目风险会对项目目标产生负面或正面的影响,也就是风险与机会。项目风险管理旨在利…...
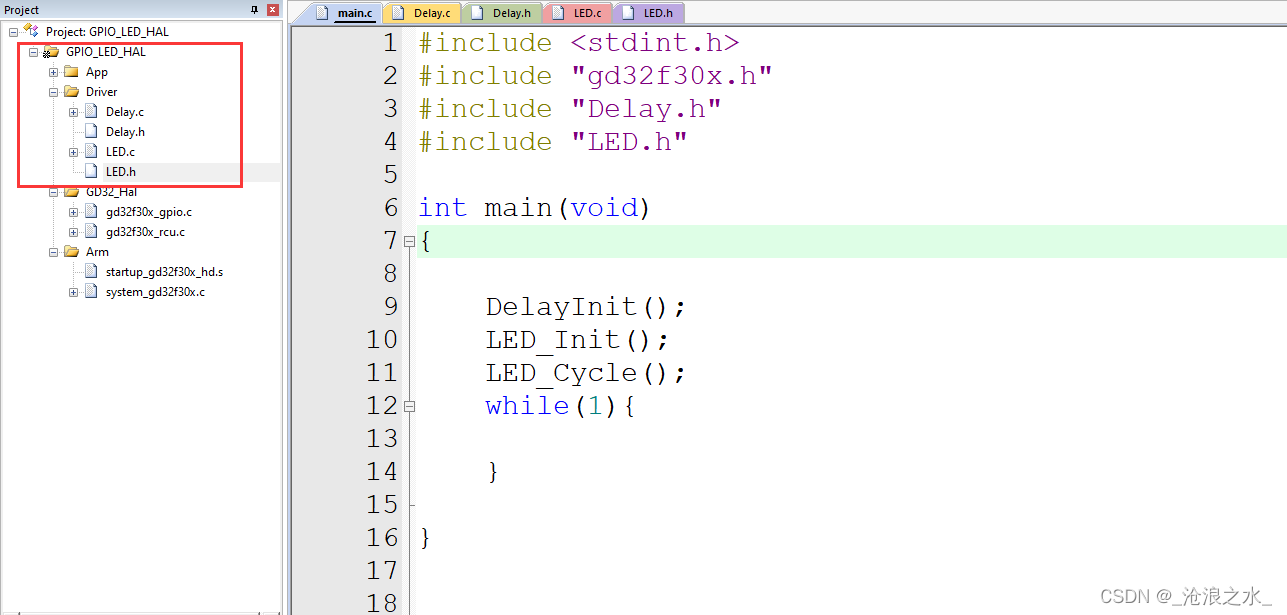
ARM单片机实现流水灯(GD32)
根据上图可知使用的引脚分别是PA8,PE6,PF6流水灯功能的实现要分别初始化这几个引脚 流水灯实现 编写流水灯代码 LED.C #include "gd32f30x.h" // Device header #include "Delay.h" // 初始化LED灯 void LED_Init(void){// 使能RCU时钟…...
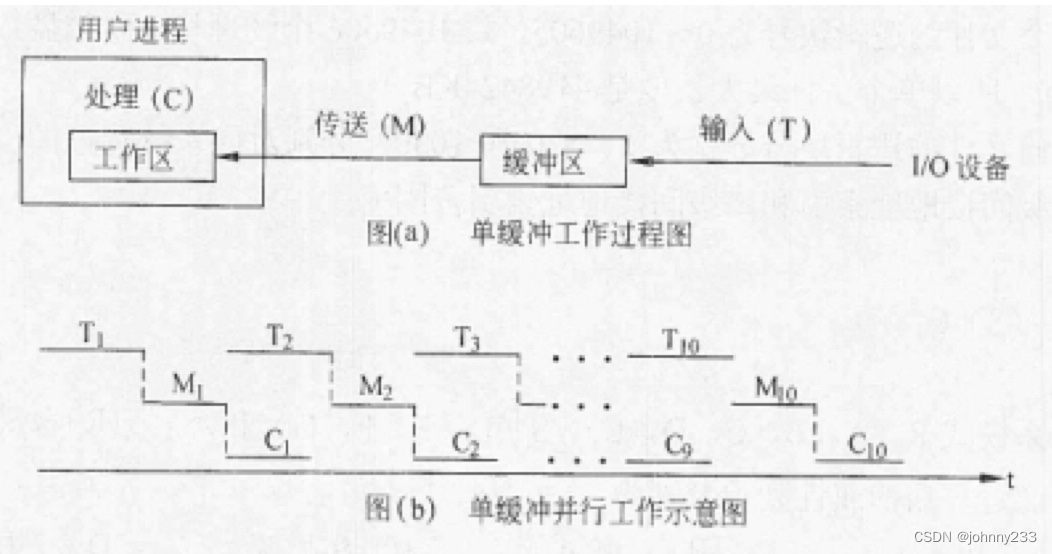
操作系统基础之磁盘
概述 基本概念 磁盘有正反两个盘面,每个盘面有多个同心圆,每个同心圆是一个磁道,每个同心圆又被划分为多个扇区,数据就被存在扇区中。 磁头首先寻找到对应磁道,然后等到磁盘进行周期旋转到指定的扇区,才…...

【Unity Shader入门精要 第6章】基础光照(一)
1. 什么是光照模型 光照原理 在真实世界中,我们能够看到物体,是由于眼睛接收到了来自观察目标的光。这里面包括两种情况:一部分是观察目标本身发出的光(自发光)直接进入我们的眼睛,另一部分是其他物体&am…...

JavaEE概述 + Maven
文章目录 一、JavaEE 概述二、工具 --- Maven2.1 Maven功能 仓库 坐标2.2 Maven之项目构建2.3 Maven之依赖管理 三、插件 --- Maven Helper 一、JavaEE 概述 Java SE、JavaEE: Java SE:指Java标准版,适用于各行各业,主要是Java…...

python把png转成jpg
在Python中,你可以使用PIL(Python Imaging Library,也称为Pillow)库来读取PNG图片并将其转换为JPG格式。下面是一个简单的示例代码: from PIL import Image# 打开PNG图片 png_image Image.open(input.png)# 保存为JP…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
