LeetCode-2391. 收集垃圾的最少总时间【数组 字符串 前缀和】
LeetCode-2391. 收集垃圾的最少总时间【数组 字符串 前缀和】
- 题目描述:
- 解题思路一:处理垃圾和路程单独计算。
- 解题思路二:逆向思维,计算多走的路
- 解题思路三:只记录,当前t需要计算几次
题目描述:
给你一个下标从 0 开始的字符串数组 garbage ,其中 garbage[i] 表示第 i 个房子的垃圾集合。garbage[i] 只包含字符 ‘M’ ,‘P’ 和 ‘G’ ,但可能包含多个相同字符,每个字符分别表示一单位的金属、纸和玻璃。垃圾车收拾 一 单位的任何一种垃圾都需要花费 1 分钟。
同时给你一个下标从 0 开始的整数数组 travel ,其中 travel[i] 是垃圾车从房子 i 行驶到房子 i + 1 需要的分钟数。
城市里总共有三辆垃圾车,分别收拾三种垃圾。每辆垃圾车都从房子 0 出发,按顺序 到达每一栋房子。但它们 不是必须 到达所有的房子。
任何时刻只有 一辆 垃圾车处在使用状态。当一辆垃圾车在行驶或者收拾垃圾的时候,另外两辆车 不能 做任何事情。
请你返回收拾完所有垃圾需要花费的 最少 总分钟数。
示例 1:
输入:garbage = [“G”,“P”,“GP”,“GG”], travel = [2,4,3]
输出:21
解释:
收拾纸的垃圾车:
- 从房子 0 行驶到房子 1
- 收拾房子 1 的纸垃圾
- 从房子 1 行驶到房子 2
- 收拾房子 2 的纸垃圾
收拾纸的垃圾车总共花费 8 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车: - 收拾房子 0 的玻璃垃圾
- 从房子 0 行驶到房子 1
- 从房子 1 行驶到房子 2
- 收拾房子 2 的玻璃垃圾
- 从房子 2 行驶到房子 3
- 收拾房子 3 的玻璃垃圾
收拾玻璃的垃圾车总共花费 13 分钟收拾完所有的玻璃垃圾。
由于没有金属垃圾,收拾金属的垃圾车不需要花费任何时间。
所以总共花费 8 + 13 = 21 分钟收拾完所有垃圾。
示例 2:
输入:garbage = [“MMM”,“PGM”,“GP”], travel = [3,10]
输出:37
解释:
收拾金属的垃圾车花费 7 分钟收拾完所有的金属垃圾。
收拾纸的垃圾车花费 15 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车花费 15 分钟收拾完所有的玻璃垃圾。
总共花费 7 + 15 + 15 = 37 分钟收拾完所有的垃圾。
提示:
2 <= garbage.length <= 105
garbage[i] 只包含字母 ‘M’ ,‘P’ 和 ‘G’ 。
1 <= garbage[i].length <= 10
travel.length == garbage.length - 1
1 <= travel[i] <= 100
解题思路一:处理垃圾和路程单独计算。
- 所有垃圾事一定要处理完的!
for g in garbage: ans += len(g) - 反向遍历
garbage数组,得到每个垃圾车需要到达的最远距离,即可计算出所需路程时间。
class Solution:def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:n = len(garbage)ans = 0for g in garbage:ans += len(g)G, M, P = 0, 0, 0for i in range(len(garbage) - 1, 0, -1):if 'G' in garbage[i]:G = ians += sum(travel[:G])breakfor i in range(len(garbage) - 1, 0, -1):if 'M' in garbage[i]:M = ians += sum(travel[:M])breakfor i in range(len(garbage) - 1, 0, -1):if 'P' in garbage[i]:P = ians += sum(travel[: P])breakreturn ans# 简化
class Solution:def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:n = len(garbage)ans = sum(map(len, garbage))for c in "GMP":for i, g in enumerate(reversed(garbage)):if c in g:ans += sum(travel[:n-i-1])breakreturn ans
时间复杂度:O(n)
空间复杂度:O(1)
解题思路二:逆向思维,计算多走的路
class Solution:def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:ans = sum(map(len, garbage)) + sum(travel) * 3for c in "MPG":for g, t in zip(reversed(garbage), reversed(travel)):if c in g:breakans -= t # 没有垃圾 c,多跑了return ans
时间复杂度:O(n)
空间复杂度:O(1)
解题思路三:只记录,当前t需要计算几次

class Solution:def garbageCollection(self, garbage: List[str], travel: List[int]) -> int:ans = len(garbage[0])seen = set()for g, t in zip(reversed(garbage), reversed(travel)):seen.update(g)ans += len(g) + t * len(seen)return ans
时间复杂度:O(n)
空间复杂度:O(n)



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠
相关文章:

LeetCode-2391. 收集垃圾的最少总时间【数组 字符串 前缀和】
LeetCode-2391. 收集垃圾的最少总时间【数组 字符串 前缀和】 题目描述:解题思路一:处理垃圾和路程单独计算。解题思路二:逆向思维,计算多走的路解题思路三:只记录,当前t需要计算几次 题目描述:…...

再有人说数字孪生大屏没有用,用这8条怼回去。
数字孪生大屏之所以受到欢迎,主要有以下几个原因: 实时数据可视化 数字孪生大屏可以将实时数据以直观的可视化形式展示出来,让用户能够一目了然地了解数据的状态和趋势。这样可以帮助用户更好地理解和分析数据,及时做出决策和调…...
蓝桥杯练习系统(算法训练)ALGO-946 Q神的足球赛
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 足球赛上,只见Q神如闪电般的速度带球时而左,时而右,时而前,时而后ÿ…...

【Android】Kotlin学习之Kotlin方法的声明和传参
方法声明 普通类的方法 静态类的方法 不需要构建实例对象, 可以通过类名直接访问静态方法 : NumUtil.double(1) companion object 伴生类的方法 使用companion object 在普通类里定义静态方法 参数 括号内传入方法 : 当参数是方法时, 并且是最后一个参数 , 可以使用括号外…...
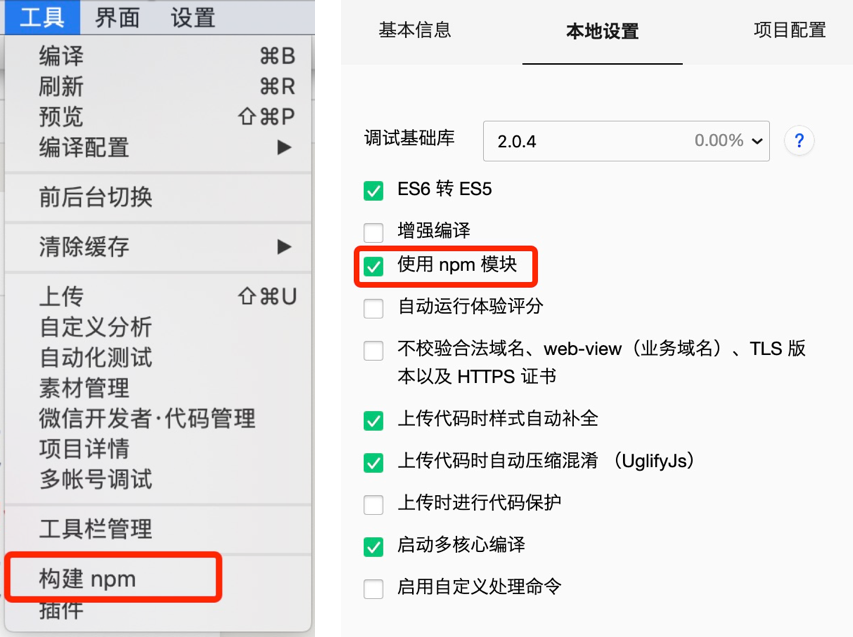
微信小程序 17:小程序使用 npm 包和组件应用
目前,小程序中已经支持实用 npm 安装第三方包,从而提高小程序的开发效率,但是在小程序中使用 npm 包有三个限制: 不支持 Node.js内置库的包不支持依赖于浏览器内置对象的包不支持依赖于 C插件的包 Vant Weapp Vant Weapp是有赞…...
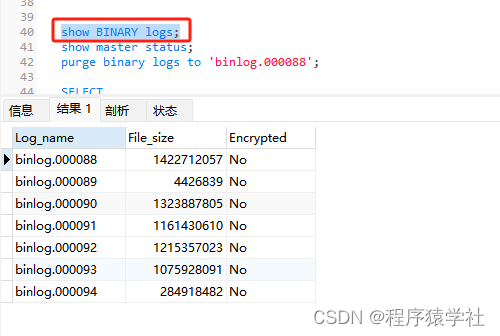
【mysql篇】执行delete删除大量数据后,磁盘未清空,为什么?
目录 迁移脚本删除数据以及备份数据 解决方法OPTIMIZE TABLE二进制日志按月生成数据 最近某个项目虽说用户量不大,但是,单表的数据量越来越大,mysql一般单表超过千万级别后,性能直线下降,所以利用shardingphere按月做了…...

【Qt 学习笔记】Qt常用控件 | 多元素控件 | Tree Widget的说明及介绍
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt常用控件 | 多元素控件 | Tree Widget的说明及介绍 文章编号&#x…...
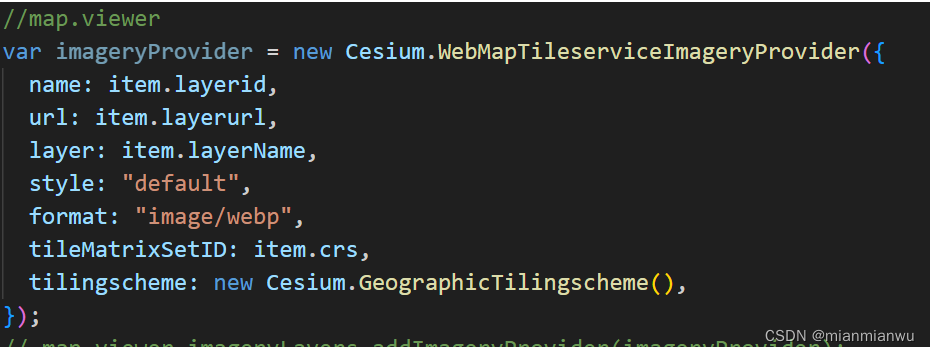
在Mars3d实现cesium的ImageryLayer自定义瓦片的层级与原点
需要自定义瓦片层级和原点,所以需要自己写第三方图层,但是之前写的很多方法,图层控制和显隐以及透明度,需要跟之前的交互一直,改动量太大的话不划算,所以直接看Mars3d的layer基类,把重写的image…...

logback日志持久化
1、问题描述 使用logback持久化记录日志。 2、我的代码 logback是Springboot框架里自带的,所以只要引入“spring-boot-starter”就行了。无需额外引入logback依赖。 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns&…...
、函数定义(Function Definition)和函数声明(Function Declaration))
函数原型(Function Prototype)、函数定义(Function Definition)和函数声明(Function Declaration)
函数原型(Function Prototype)、函数定义(Function Definition)和函数声明(Function Declaration)在C和C等编程语言中扮演着不同的角色,但它们有时在概念上可能会有些重叠。下面是它们之间的主要…...

Go有无缓冲channel的区别
无缓冲的channel channel的默认类型就是无缓冲的。当一个数据被发送到无缓冲的channel中,发送操作会被阻塞,知道有另一个goroutine从这个channel中接收这个数据。同样,当试图从一个无缓冲的channel中接收数据时,如果没有数据可以…...
【全开源】Fastflow工作流系统(源码搭建/上线/运营/售后/维护更新)
一款基于FastAdminThinkPHP开发的可视化工作流程审批插件,帮助用户基于企业业务模式和管理模式自行定义所需的各种流程应用,快速构建企业自身的流程管控体系,快速融合至企业协同OA办公系统。 提供全部无加密服务端源码和前端源代码࿰…...

超越传统游戏:生成式人工智能对游戏的变革性影响
人工智能(AI)在游戏中的应用 游戏产业是一个充满活力、不断发展的领域,人工智能(AI)的融入对其产生了重大影响。这一技术进步彻底改变了游戏的开发、玩法和体验方式。本文分析的重点是传统人工智能和生成式人工智能在游…...

SpringCloud微服务之Eureka、Ribbon、Nacos详解
SpringCloud微服务之Eureka、Ribbon、Nacos详解 1、认识微服务1.1、单体架构1.2、分布式架构1.3、微服务1.4、SpringCloud 2、服务拆分与远程调用2.1、服务拆分的原则2.2、服务拆分示例2.2、提供者与消费者 3、Eureka注册中心3.1、Eureka的结构和作用3.2、搭建eureka-server3.2…...
五角钱的程序员 | Kafka 是什么?
本文来源公众号“五角钱的程序员”,仅用于学术分享,侵权删,干货满满。 原文链接:Kafka 是什么? 你是一个程序员,假设你维护了两个服务 A 和 B。B 服务每秒只能处理 100 个消息,但 A 服务却每秒…...

C++中合成的默认构造函数的访问权限
问题 我们知道,在C中,如果没有为一个类显式定义构造函数,那么编译器会为我们隐式地定义一个默认构造函数。那么,你有没有想过,这个隐式定义的默认构造函数(合成的默认构造函数)的访问权限是什么…...
【前端】桌面版docker并部署前端项目
环境 win10专业版 2004 , 需科学 官网下载安装包并安装4.29.0版本 终端输入 wsl --installdocker桌面版和模拟器只能选一个,不然一直转圈圈 镜像配置加速,在settings—>docker engine下 {"builder": {"gc": {"defaultKee…...

发布GPT-5的方式可能会与以往不同;开源vocode使用 AI 自动拨打电话;开源gpt智能对话客服工具;AI自动写提示词
✨ 1: vocode 用AI通过声音与用户进行实时交流 Vocode是一个旨在帮助开发者快速构建基于声音的大型语言模型(LLM)应用程序的开源库。简单来说,如果你想要开发一个能够通过声音与用户进行实时交流的应用,比如电话机器人、语音助手…...
)
Linux 作业管理 (bg, fg, jobs, kill)
bg 和 fg 是用来管理作业(在 Unix/Linux 命令行下运行的进程)的命令。 1. bg 命令 bg 命令用于将作业(job)放到后台运行。当你在终端中运行一个命令或程序时,它会占用当前终端的控制,如果你想让这个任务在…...
 包括注解@Cache)
springboot Redis 支持星号(*) 包括注解@Cache
通过自定义CacheManager Bean来实现 bean Autowiredprivate RedisConnectionFactory redisConnectionFactory;/*** 管理缓存** return*///缓存管理器PrimaryBeanOverridepublic CacheManager cacheManager() {// 使用自定义的缓存配置初始化一个cacheManagerreturn new Custom…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
