LeetCode题练习与总结:二叉树的中序遍历--94
一、题目描述
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
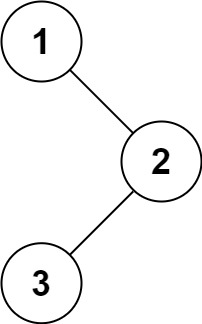
输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
二、递归方法
(一)解题思路
- 如果当前节点为空,返回。
- 递归遍历左子树。
- 访问当前节点,将节点的值添加到结果列表中。
- 递归遍历右子树。
(二)具体代码
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorder(root, result);return result;}private void inorder(TreeNode node, List<Integer> result) {if (node == null) {return;}inorder(node.left, result);result.add(node.val);inorder(node.right, result);}
}
(三)时间复杂度和空间复杂度
1. 时间复杂度
- 递归方法会访问树中的每个节点恰好一次,因此时间复杂度与树中节点的数量成正比。
- 在这个算法中,每个节点都会被访问一次,所以时间复杂度是 O(n),其中 n 是二叉树中的节点数。
2. 空间复杂度
- 递归方法的空间复杂度主要取决于递归栈的深度,这通常与树的高度成正比。
- 在最坏的情况下,树完全不平衡,每个节点都只有左子节点或者只有右子节点,递归栈的深度会达到节点数 n,因此空间复杂度为 O(n)。
- 在最好的情况下,树是完全平衡的,递归栈的深度是 log(n),因此空间复杂度为 O(log(n))。
- 综合考虑,空间复杂度在最坏情况下是 O(n),在最好情况下是 O(log(n)),平均情况下则介于两者之间。
综上所述,递归方法的中序遍历代码的时间复杂度是 O(n),空间复杂度在最坏情况下是 O(n),在最好情况下是 O(log(n))。
(四)总结知识点
1. 递归(Recursion):
- 代码中使用了递归函数
inorder来遍历二叉树的左子树、根节点和右子树。 - 递归是一种常用的算法设计技巧,它通过函数自身调用自己来进行循环。
2. 二叉树(Binary Tree):
- 代码操作的数据结构是二叉树,每个节点包含一个值和指向左右子节点的引用。
- 二叉树是一种基础的数据结构,常用于各种算法问题。
3. 二叉树的中序遍历(Inorder Traversal of a Binary Tree):
- 中序遍历是一种遍历二叉树的方法,按照“左-根-右”的顺序访问每个节点。
- 这是二叉树遍历的三种基本方法之一(其他两种是前序遍历和后序遍历)。
4. Java 集合框架(Java Collections Framework):
- 代码使用了
ArrayList来存储遍历的结果,这是 Java 集合框架中的一个类。 ArrayList是一个可调整大小的数组实现,提供了对元素的快速随机访问。
5. 函数定义和调用(Function Definition and Invocation):
- 代码定义了两个函数:
inorderTraversal和inorder。 inorderTraversal是公共方法,供外部调用;inorder是私有辅助方法,用于递归遍历。
6. 基本语法(Basic Syntax):
- 代码使用了基本的 Java 语法,如类定义、方法定义、条件语句(if)、返回语句(return)等。
7. 递归栈(Recursive Stack):
- 虽然代码中没有显式使用栈数据结构,但递归函数在调用时会使用调用栈来存储每一层递归的状态。
三、迭代方法
(一)解题思路
- 初始化一个空栈和一个空列表。
- 将根节点及其所有左子节点入栈。
- 弹出栈顶元素,将其值添加到结果列表中。
- 将弹出节点的右子节点及其所有左子节点入栈。
- 重复步骤3和4,直到栈为空。
(二)具体代码
import java.util.Stack;class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode current = root;while (current != null || !stack.isEmpty()) {while (current != null) {stack.push(current);current = current.left;}current = stack.pop();result.add(current.val);current = current.right;}return result;}
}
(三)时间复杂度和空间复杂度
1. 时间复杂度
- 中序遍历需要访问二叉树中的每个节点一次,因此时间复杂度与二叉树中节点的数量成正比。
- 在这个算法中,每个节点都会被访问一次,所以时间复杂度是 O(n),其中 n 是二叉树中的节点数。
2. 空间复杂度
- 空间复杂度主要取决于迭代过程中使用的栈的大小。
- 在最坏的情况下,树完全不平衡,每个节点都只有左子节点或者只有右子节点,栈的大小会达到节点数 n,因此空间复杂度为 O(n)。
- 在最好的情况下,树是完全平衡的,栈的大小是 log(n),因此空间复杂度为 O(log(n))。
- 综合考虑,空间复杂度在最坏情况下是 O(n),在最好情况下是 O(log(n)),平均情况下则介于两者之间。
综上所述,这段代码的时间复杂度是 O(n),空间复杂度在最坏情况下是 O(n),在最好情况下是 O(log(n))。
(四)总结知识点
1. 迭代(Iteration):
- 代码使用了一个循环结构来迭代地遍历二叉树的节点,而不是使用递归。
2. 栈(Stack)数据结构:
- 代码使用了一个
Stack来存储访问过的节点,以便后续能够按照正确的顺序访问它们的右子节点。 - 栈是一种后进先出(LIFO)的数据结构,非常适合用于这种需要回溯的场景。
3. 二叉树(Binary Tree):
- 代码操作的数据结构是二叉树,每个节点包含一个值和指向左右子节点的引用。
- 二叉树是一种基础的数据结构,常用于各种算法问题。
4. 二叉树的中序遍历(Inorder Traversal of a Binary Tree):
- 中序遍历是一种遍历二叉树的方法,按照“左-根-右”的顺序访问每个节点。
- 这是二叉树遍历的三种基本方法之一(其他两种是前序遍历和后序遍历)。
5. Java 集合框架(Java Collections Framework):
- 代码使用了
ArrayList来存储遍历的结果,这是 Java 集合框架中的一个类。 ArrayList是一个可调整大小的数组实现,提供了对元素的快速随机访问。- 同时,代码使用了
Stack类来实现栈数据结构。
6. 循环和条件语句(Loop and Conditional Statements):
- 代码使用了
while循环来迭代遍历树节点,并使用了if语句来检查当前节点是否为空。
7. 函数定义和调用(Function Definition and Invocation):
- 代码定义了一个公共方法
inorderTraversal,供外部调用。
8. 基本语法(Basic Syntax):
- 代码使用了基本的 Java 语法,如类定义、方法定义、循环结构、条件语句等。
以上就是解决这个问题的详细步骤,希望能够为各位提供启发和帮助。
相关文章:

LeetCode题练习与总结:二叉树的中序遍历--94
一、题目描述 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 示例 1: 输入:root [1,null,2,3] 输出:[1,3,2]示例 2: 输入:root [] 输出:[]示例 3: 输入:roo…...
云计算十三课
centos安装 点击左上角文件 点击新建虚拟机 点击下一步 点击稍后安装操作系统,下一步 选择Linux(l)下一步 设置虚拟机名称 点击浏览选择安装位置 新建文件夹设置名称不能为中文,点击确定 点击下一步 设置磁盘大小点击下一步…...

[数据集][目标检测]电力场景安全帽检测数据集VOC+YOLO格式295张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):295 标注数量(xml文件个数):295 标注数量(txt文件个数):295 标注类别…...

AtCoder Beginner Contest 308 A题 New Scheme
A题:New Scheme 标签:模拟 题意:给定 8 8 8个数的序列,询问这些数是否满足以下条件: 在 100 100 100到 675 675 675之间且能被 25 25 25整除序列是单调非递减的 题解:按题意模拟判断就好了。 代码&#…...

C++编程与朱元墇的关系
学编程和英语没关系,我说这句话,没人会相信,也不会有人说我什么哗众取宠。 我说学编程和朱元墇有关系,一定有人说我放P,其实这个P也和朱元墇有关系, 和朱元墇有什么P关系啊。 真有这P事啊, 朱元…...

0060__设计模式
1. 简单工厂模式( Simple Factory Pattern ) — Graphic Design Patterns 工厂模式 | 菜鸟教程 【设计模式——学习笔记】23种设计模式——建造者模式Builder(原理讲解应用场景介绍案例介绍Java代码实现)-CSDN博客 设计模式—— 五:迪米特…...
【Linux 网络】网络编程套接字 -- 详解
⚪ 预备知识 1、理解源 IP 地址和目的 IP 地址 举例理解:(唐僧西天取经) 在 IP 数据包头部中 有两个 IP 地址, 分别叫做源 IP 地址 和目的 IP 地址。 如果我们的台式机或者笔记本没有 IP 地址就无法上网,而因为…...

编译OpenResty遇到找不到OpenSSL的解决办法
以OpenResty-1.19.9.1为例 编辑openresty-1.19.9.1/build/nginx-1.19.9/auto/lib/openssl/conf CORE_INCS"$CORE_INCS $OPENSSL/.openssl/include" CORE_DEPS"$CORE_DEPS $OPENSSL/.openssl/include/openssl/ssl.h" CORE_LIBS"$CORE_LIBS $OPENSSL/.…...

Amazon Bedrock 托管 Llama 3 8B70B
Amazon Bedrock 托管 Llama 3 8B&70B,先来体验:(*实验环境账号有效期为1天,到期自动关停,请注意重要数据保护) https://dev.amazoncloud.cn/experience/cloudlab?id65fd86c7ca2a0d291be26068&visi…...

海豚调度器早期版本如何新增worker分组
在DolphinScheduler 1.3.5版本中,Worker分组通常是在部署时通过配置文件进行定义的,而不是在用户界面上直接操作。以下是在DolphinScheduler中新增Worker分组的一般步骤: 修改配置文件: DolphinScheduler的Worker分组信息通常在/…...

Debian Linux 下给Nginx 1.26.0 编译增加Brotli算法支持
明月发现参考【给Nginx添加谷歌Brotli压缩算法支持】一文给出的方法,在Debian Linux 12.5下就一直编译失败,主要的错误是因为文件缺失,在专门又安装了apt-get install libbrotli-dev的依赖库后依然会因为文件缺失无法编译完成,就这…...

中国银行从业在线教育系统,如何搭建网课平台?
如今这个时代相信没多少人是没听过网课平台的,绝大多数人对网课平台的名气是如雷贯耳的。时代的发展,让人们学习的方式变得更加的方便与快捷。今天就来和大家说说网课平台搭建都有哪些方法?网课平台难搭建么? 网课平台搭建的方法,其实网课平…...

解决java.lang.IllegalArgumentException异常的正确方法
java.lang.IllegalArgumentException 是 Java 中的一个异常类,表示方法中传递的参数不合法。这个异常通常在方法被调用时抛出,表明方法的参数出现了问题。要正确解决这个异常,你可以按照以下步骤进行: 查看异常信息:首…...

齿轮滚刀刃口钝化技术简介
介绍 在滚刀的使用中发现,进口滚刀和国产滚刀在加工质量和寿命方面存在显著差异。经过多次比较得知,滚刀的使用寿命可以达到国产滚刀的两倍以上,而进口滚刀返回原厂磨削后的使用寿命约为新刀具的90% ,但同样经过国内厂家磨削后&a…...

【ESP32接入ATK-MO1218 GPS模块】
【ESP32接入ATK-MO1218 GPS模块】 1. 引言2. ATK-MO1218 GPS模块概述3. 接入ATK-MO1218 GPS模块的步骤4. 示例代码5. 结论1. 引言 在现代的嵌入式系统和物联网项目中,精确的位置信息是至关重要的。ATK-MO1218 GPS模块作为一款高性能的GPS/北斗双模定位模块,为开发者提供了强…...
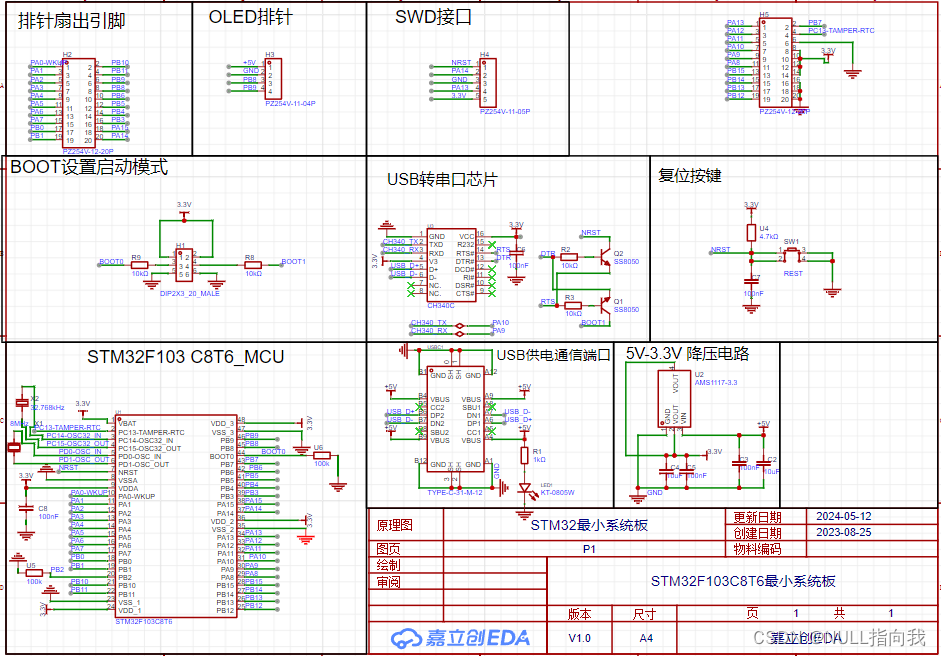
EDA设计学习笔记2:STM32F103C8T6最小系统板的仿绘
今日开始仿制练习一个STM32F103C8T6最小系统板,通过对这个最小系统板的仿制,达到对自己PCB设计的练习的目的,最终目标是自己设计出一块PCB,做一个OLED的桌面小摆件...... 也不知道画出来能不能用..... 目录 主控芯片的搜索与放置…...
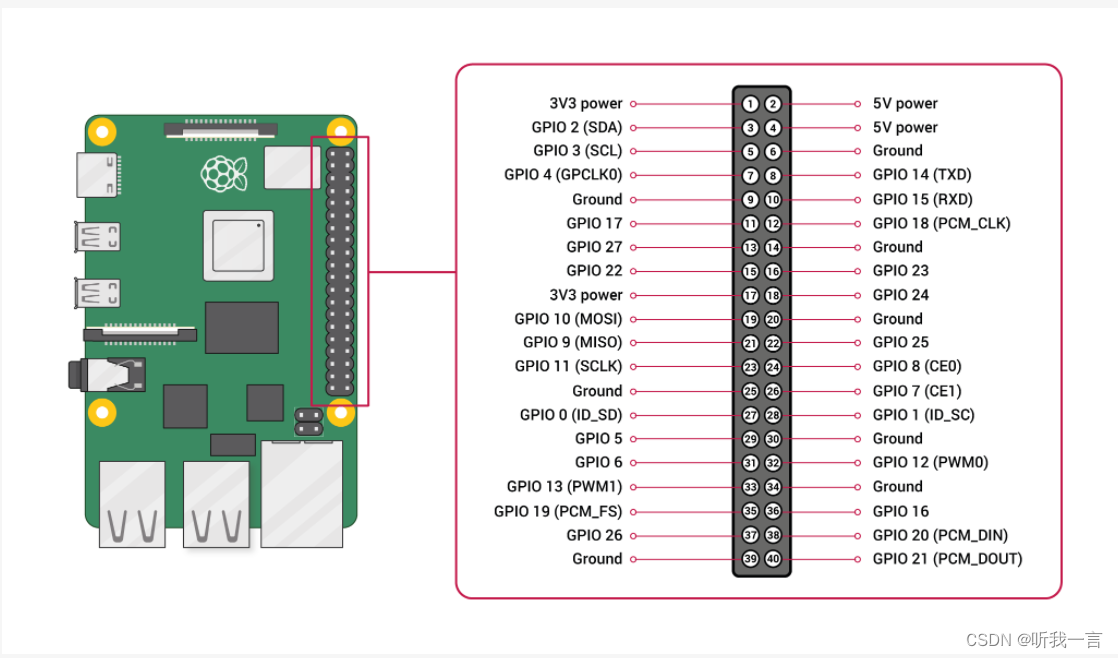
实现树莓派DS18B20读取温度(OneWire)
简介 使用的是树莓派3B, Go编程实现OneWire方式读取DS18B20温度。 接线 DS18B20 包含经典三线, VCC和GND自不必说, 主要的是DQ线, 需要接4.7K的上拉电阻, 即4.7K欧姆的电阻接到DQ和VCC, 否则树莓派识别不到DS18B20&am…...
)
Android 蓝牙实战——蓝牙音乐播放/暂停状态(二十二)
对于蓝牙音乐的播放状态,我们首先主要处理的是 onPlayStatusChanged() 回调,这是协议栈通知 FW 层的一个回调接口。还有一个就是 getPlayBackState() 方法,这是媒体应用在初始化时未收到回调信息主动获取当前状态的方法。我们这里就来分析一下这两个状态的获取流程。 一、状…...
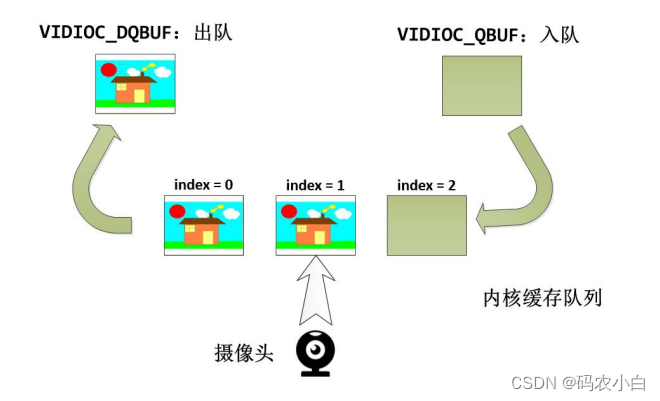
linux学习:视频输入+V4L2
目录 V4L2 视频采集流程 代码例子 核心命令字和结构体 VIDIOC_ENUM_FMT VIDIOC_G_FMT / VIDIOC_S_FMT / VIDIOC_TRY_FM VIDIOC_REQBUFS VIDIOC_QUERYBUF VIDIOC_QBUF /VIDIOC_DQBUF VIDIOC_STREAMON / VIDIOC_STREAMOFF V4L2 是 Linux 处理视频的最新标准代码模块&…...
[AutoSar]BSW_Diagnostic_004 ReadDataByIdentifier(0x22)的配置和实现
目录 关键词平台说明背景一、配置DcmDspDataInfos二、配置DcmDspDatas三、创建DcmDspDidInfos四、创建DcmDspDids五、总览六、创建一个ASWC七、mapping DCM port八、打开davinci developer,创建runnabl九、生成代码 关键词 嵌入式、C语言、autosar、OS、BSW、UDS、…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...
