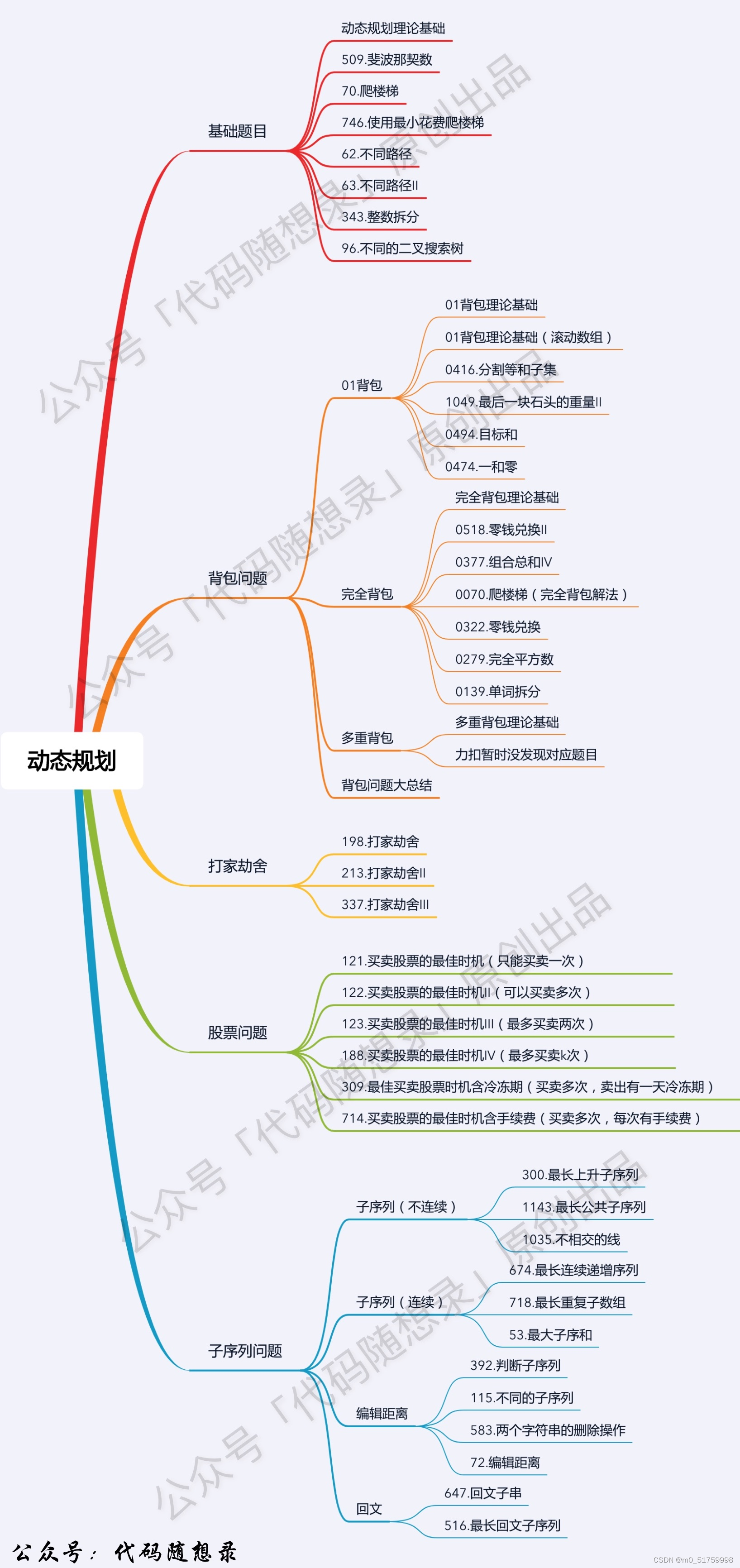
代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
文章目录
- 代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
- 理论基础
- 一、常规题目
- 二、解题步骤
- 509. 斐波那契数
- 一、动态规划v1
- 二、动态规划v2
- 三、动态规划v3
- 70. 爬楼梯
- 一、动态规划v1
- 二、动态规划v2
- 746. 使用最小花费爬楼梯
- 一、dp v1
- 二、dp v2
理论基础
一、常规题目
二、解题步骤
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
509. 斐波那契数
题目链接
- 确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]- 确定递推公式
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];- dp数组如何初始化
题目中把如何初始化也直接给我们了,如下: dp[0] = 0; dp[1] = 1;- 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的- 打印dp数组
一、动态规划v1
class Solution:def fib(self, n):# 排除 Corner Caseif n == 0:return 0# 创建 dp table dp = [0] * (n + 1)# 初始化 dp 数组dp[0] = 0dp[1] = 1# 遍历顺序: 由前向后。因为后面要用到前面的状态for i in range(2, n + 1):# 确定递归公式/状态转移公式dp[i] = dp[i - 1] + dp[i - 2]# 返回答案return dp[n
二、动态规划v2
class Solution:def fib(self, n):if n<=1:return ndp=[0,1]for i in range(2,n+1):total = dp[0]+dp[1]dp[0]=dp[1]dp[1]=total return total
三、动态规划v3
class Solution:def fib(self, n):if n<=1:return nprev0,prev1 = 0,1for _ in range(2,n+1):cur = prev0 + prev1prev0,prev1 = prev1,curreturn cur
70. 爬楼梯
题目链接
- 确定dp数组以及下标的含义
dp[i]的定义为:爬到第i层楼梯,有dp[i]种方法- 确定递推公式
dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么
状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];- dp数组如何初始化
dp[1] = 1; dp[2] = 2;- 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的- 打印dp数组
一、动态规划v1
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""dp = [0]*(n+1)if n <=2:return ndp[1]=1dp[2]=2for i in range(3,n+1):dp[i]=dp[i-1]+dp[i-2]return dp[n]
二、动态规划v2
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""dp=[0,1,2]if n <=2:return nfor i in range(3,n+1):total = dp[1]+dp[2]dp[1]=dp[2]dp[2]=totalreturn total
746. 使用最小花费爬楼梯
题目链接
- 确定dp数组以及下标的含义
dp[i]的定义为:到达第i台阶所花费的最少体力为dp[i]- 确定递推公式
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]
状态转移方程 : dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);- dp数组如何初始化
dp[0] = 0; dp[1] = 0;- 确定遍历顺序
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了- 打印dp数组
一、dp v1
class Solution(object):def minCostClimbingStairs(self, cost):""":type cost: List[int]:rtype: int"""dp = [0] * (len(cost) + 1)dp[0] = 0 # 初始值,表示从起点开始不需要花费体力dp[1] = 0 # 初始值,表示经过第一步不需要花费体力for i in range(2, len(cost) + 1):# 在第i步,可以选择从前一步(i-1)花费体力到达当前步,或者从前两步(i-2)花费体力到达当前步# 选择其中花费体力较小的路径,加上当前步的花费,更新dp数组dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])return dp[len(cost)] # 返回到达楼顶的最小花费
二、dp v2
class Solution(object):def minCostClimbingStairs(self, cost):""":type cost: List[int]:rtype: int"""dp0=0dp1=0for i in range(2,len(cost)+1):dp2=min(dp1+cost[i-1],dp0+cost[i-2])dp0=dp1dp1=dp2return dp2
相关文章:

代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯
代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯 文章目录 代码随想录算法训练营Day 38| 动态规划part01 | 理论基础、509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯理论基础一、常规题目二、解题步骤…...

CSS拟物按钮
<div class"btn">F</div>.btn {margin: 150px 0 0 150px;display: flex;justify-content: center;align-items: center;width: 100px;height: 100px;background-color: #fff;border-radius: 20px;font-size: 50px;color: #333;/* 禁止选中文本 */user-se…...

websevere服务器从零搭建到上线(三)|IO多路复用小总结和服务器的基础框架
文章目录 epollselect和poll的优缺点epoll的原理以及优势epoll 好的网络服务器设计Reactor模型图解Reactor muduo库的Multiple Reactors模型 epoll select和poll的优缺点 1、单个进程能够监视的文件描述符的数量存在最大限制,通常是1024,当然可以更改数…...
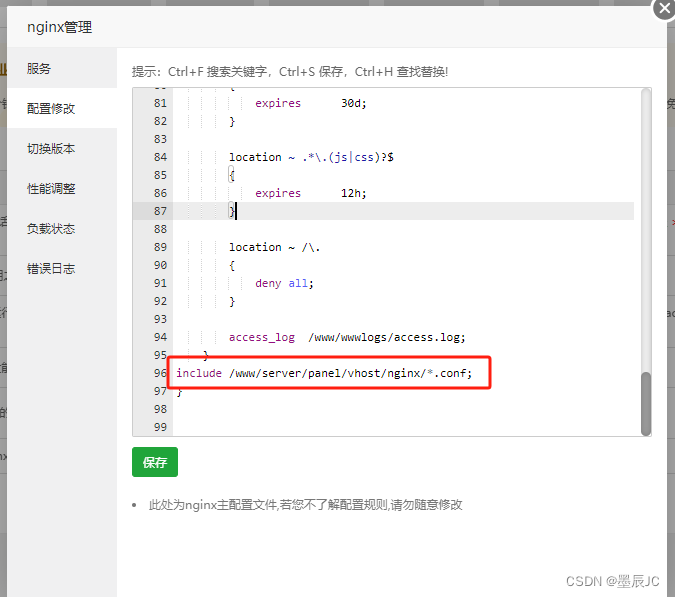
解决宝塔Nginx和phpMyAdmin配置端口冲突问题
问题描述 在对基于宝塔面板的 Nginx 配置文件进行端口修改时,我注意到 phpMyAdmin 的端口配置似乎也随之发生了变化! 解决方法 官方建议在处理 Nginx 配置时,应避免直接修改默认的配置文件,以确保系统的稳定性和简化后续的维护…...
光伏EPC管理软件都有哪些功能和作用?
光伏EPC管理软件是用于光伏工程项目管理的综合性工具,它涵盖了从项目策划、设计、采购、施工到运维的各个环节。 1、项目总览 管理所有项目计划,包括项目类型、项目容量等。 调整和优化项目计划,以应对不可预见的情况。 2、施工管理 制定…...
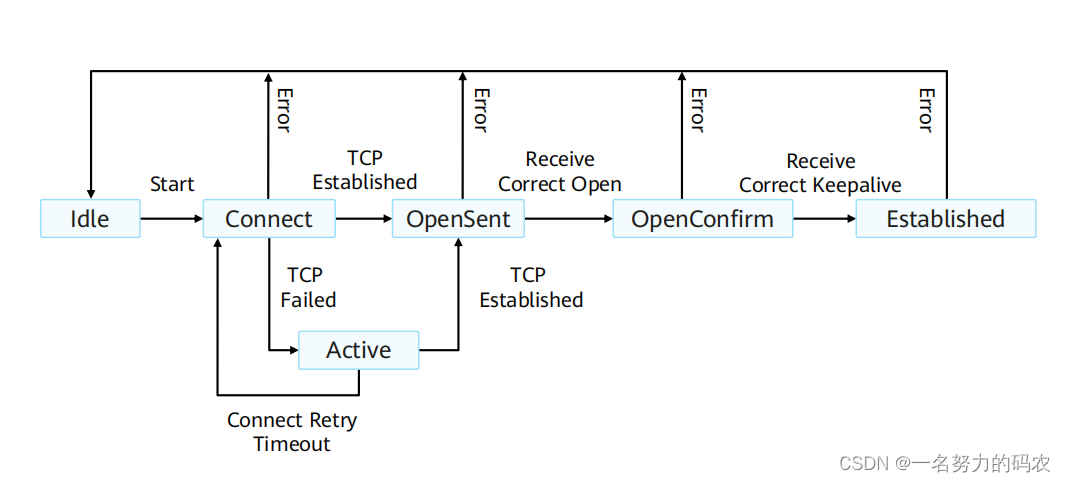
BGP学习一:关于对等体建立和状态组改变
目录 一.BGP基本概念 (1).BGP即是协议也是分类 1.早期EGP 2.BGP满足不同需求 3.BGP区域间传输的优势 (1)安全性——只传递路由信息 (2)跨网段建立邻居 4.BGP总结 5.BGP的应用 (1&#…...
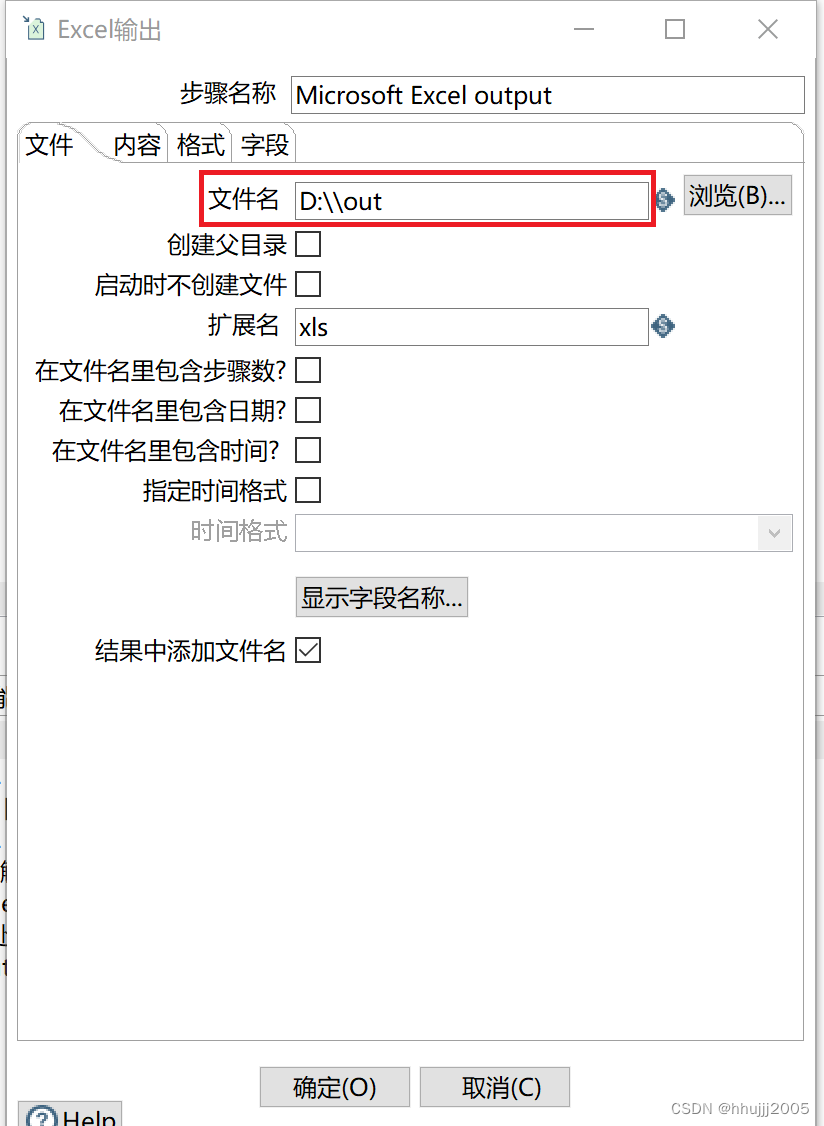
ETL工具kettle(PDI)入门教程,Transform,Mysql->Mysql,Csv->Excel
什么是kettle,kettle的下载,安装和配置:ETL免费工具kettle(PDI),安装和配置-CSDN博客 mysql安装配置:Linux Centos8 Mysql8.3.0安装_linux安装mysql8.3-CSDN博客 1 mysql -> mysql 1.1 mysql CREATE TABLE user_…...

常见地图坐标系间的转换算法JavaScript实现
文章目录 🍉 不同的地图厂商使用不同的坐标系来表示地理位置。以下简述:🍉 前置常量和方法:🍉 BD-09转GCJ-02(百度转谷歌、高德)🍉 GCJ-02转BD-09(谷歌、高德转百度)🍉 WGS84转GCJ-02(WGS84转谷歌、高德)🍉 GCJ-02转WGS84(谷歌、高德转WGS84)🍉 BD-09转wgs84坐…...

基于python的大麦网自动抢票工具的设计与实现
基于python的大麦网自动抢票工具的设计与实现 Design and Implementation of Da Mai Net Ticket Grabbing tool based on Python 完整下载链接:基于python的大麦网自动抢票工具的设计与实现 文章目录 基于python的大麦网自动抢票工具的设计与实现摘要第一章 引言1.1 研究背景…...

2024年5月树莓集团快讯
树莓集团近期快讯 1 园区专场招聘会进校园 国际数字影像产业园联合四川城市职业学院的专场招聘会成功召开,共计提供400余个工作岗位。 2 园区硬件优化再升级 园区硬件优化再升级,智能门禁系统及人脸识别系统下周投入使用。 3 基地短剧合作交流 天府…...

网站localhost和127.0.0.1可以访问,本地ip不可访问解决方案
部署了一个网站, 使用localhost和127.0.0.1加端口号可以访问, 但是使用本机的ip地址加端口号却不行. 原因可能有多种. 可能的原因: 1 首先要确认是否localhost对应的端口是通的(直接网址访问), 以及你无法访问的那个本机ip是否正确(使用ping测试); 2 检查本机的防火…...

Docker Dockerfile如何编写?
Dockerfile 是一个用来构建镜像的文本文件,文本内容包含了一条条构建镜像所需的指令和说明。 1.指令说明 FROM,构建镜像基于哪个镜像 MAINTAINER,镜像维护者姓名或邮箱地址 RUN,构建镜像时运行的指令 CMD,运行容器时执…...

Python数独游戏
数独(Sudoku)是一种逻辑性的数字填充游戏,玩家需要在一个分为九宫的81格网格上填入数字,同时满足每一行、每一列以及每个宫(3x3的子网格)的数字都不重复。 在Python中实现一个数独游戏可以涉及到多个方面&…...
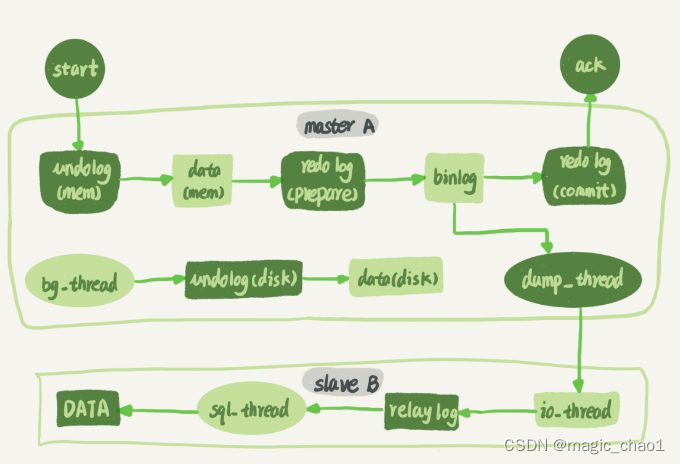
24 | MySQL是怎么保证主备一致的?
MySQL 主备的基本原理 内部流程 备库 B 跟主库 A 之间维持了一个长连接。主库 A 内部有一个线程,专门用于服务备库 B 的这个长连接。一个事务日志同步的完整过程是这样的: 在备库 B 上通过 change master 命令,设置主库 A 的 IP、端口、用户名、密码,以及要从哪个位置开始…...

2.数据类型与变量(java篇)
目录 数据类型与变量 数据类型 变量 整型变量 长整型变量 短整型变量 字节型变量 浮点型变量 双精度浮点型 单精度浮点型 字符型变量 布尔型变量(boolean) 类型转换 自动类型转换(隐式) 强制类型转换(显式) 类型提升 字符串类型 数据类…...

QT设计模式:桥接模式
基本概念 桥接模式是一种结构型设计模式,它将抽象部分与它的实现部分分离,使得它们可以独立地变化,而不会相互影响。 需要实现的结构如下: 抽象部分(Abstraction):定义了抽象类的接口&#x…...

简单粗暴的翻译英文pdf
背景:看书的时候经常遇到英文pdf,没有合适的翻译软件可以快速翻译全书。这里提供一个解决方案。 Step 1 打开英文pdfCTRLA全选文字CTRLC复制打开记事本CTRLV复制保存为data.txt Step 2 写一个C脚本 // ToolPdf2Html.cpp : 此文件包含 "main&quo…...
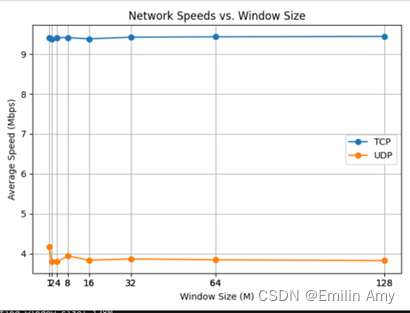
UDP和TCP协议比较,TOE技术
如今在某些方面TCP超越UDP的主要原因如下 在硬件层面的TOE(TCP Offload Engine)功能,将越来越多的TCP功能卸载到网卡上。它极大地提升了TCP的性能,使其在高吞吐量场景下的表现更为出色。近年TCP的拥塞控制算法实现了显著进步。这些新算法显著提高了TCP在…...

第十三节 huggingface的trainner解读与Demo
文章目录 前言一、trainer和TrainingArguments训练与预测完整Demo1、数据构建2、TrainingArguments构建3、Trainer初始化4、模型训练5、模型推理6、完整demo代码7、完整运行结果二、辅助函数1、yield返回内容2、迭代器中断恢复迭代demo3、yield from结构4、torch.Generator()的…...

GO: json 处理
需要引入"encoding/json"包 json解析到map jsonStr : "{\"a\":\"test\",\"b\":\"testb\"}" var dat map[string]string err : json.Unmarshal([]byte(jsonStr), &dat) if err nil {fmt.Println(dat) }结果…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...
