Python 运筹优化13 Thompson Sampling 解读
说明
这部分应该是Multi-Armed Bandit的最后一部分了。
内容
1 On Line Ads
这个实验,最初的目的就是为了选出最佳的广告。首先,通过伯努利分布,模拟了某个广告的有效率。在真实场景里,我们是无法知道那个广告更好的。可能在train阶段,可以获得一些模糊的参考,但是使用强化学习的目的,就是让其随着现实返回进行自发调整。
可以把一个模型,或者一个版本视为一个bandit。强化框架的意义在于最大化的利用已有的一套bandit,在过程中,最优的bandit会自动浮现,从而解开最初建模阶段的一些迷惑。
class BernoulliBandit(object):def __init__(self, p):self.p = pdef display_ad(self):reward = np.random.binomial(n=1, p=self.p)return rewardadA = BernoulliBandit(0.004)
adB = BernoulliBandit(0.016)
adC = BernoulliBandit(0.02)
adD = BernoulliBandit(0.028)
adE = BernoulliBandit(0.031)ads = [adA, adB, adC, adD, adE]
2 强化学习
在之前的样例中,我们已经尝试了A/B/n test 、eps greedy、UCB等三个方法,现在是最后一种方法Thompson Sampling
初始化过程 :
这段代码看起来像是为Multi-Armed Bandit Proble 中的 Thompson Sampling 算法做准备。Thompson Sampling 是一种用于解决探索-利用困境的随机化算法,它基于贝叶斯方法,在每个时间步骤根据先验分布和观察到的奖励来更新每个臂的概率分布。
在 Thompson Sampling 中,每个臂都有一个 Beta 分布,其中 α 参数表示已经获得的奖励次数,β 参数表示已经尝试的次数减去获得奖励的次数。在每个时间步骤,根据每个臂的 Beta 分布随机抽样,选择具有最大样本值的臂作为当前时间步的动作。
n_prod = 100000
n_ads = len(ads)
alphas = np.ones(n_ads)
betas = np.ones(n_ads)
total_reward = 0
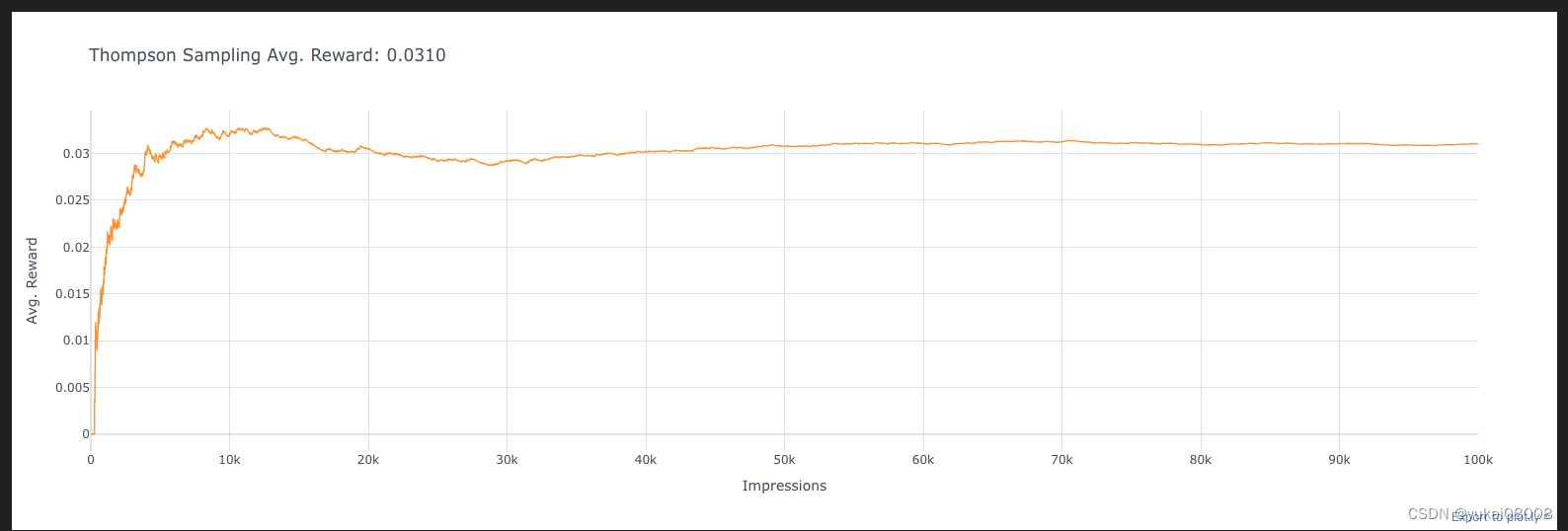
avg_rewards = []for i in range(n_prod):theta_samples = [np.random.beta(alphas[k], betas[k]) for k in range(n_ads)]ad_chosen = np.argmax(theta_samples)R = ads[ad_chosen].display_ad()alphas[ad_chosen] += Rbetas[ad_chosen] += 1 - Rtotal_reward += Ravg_reward_so_far = total_reward / (i + 1)avg_rewards.append(avg_reward_so_far)
df_reward_comparison['Thompson Sampling'] = avg_rewards
这段代码做了以下几件事情:
对于每个时间步骤 i,从每个臂的 Beta 分布中采样一个值 theta_samples。
选择具有最大 theta_samples 的臂作为当前时间步骤的动作 ad_chosen。
显示所选择广告,并获取奖励 R。
根据获得的奖励更新所选臂的 Alpha 和 Beta 参数。
计算当前总奖励 total_reward 和平均奖励 avg_reward_so_far。
将平均奖励添加到 avg_rewards 列表中。
将 avg_rewards 列表添加到 DataFrame 中,命名为 ‘Thompson Sampling’。
3 UCB
这个漏掉了,补一下
分别使用3个参数分别跑
# c = 0.1
# c = 1
c =10
n_prod = 100000
n_ads = len(ads)
ad_indices = np.array(range(n_ads))
Q = np.zeros(n_ads)
N = np.zeros(n_ads)
total_reward = 0
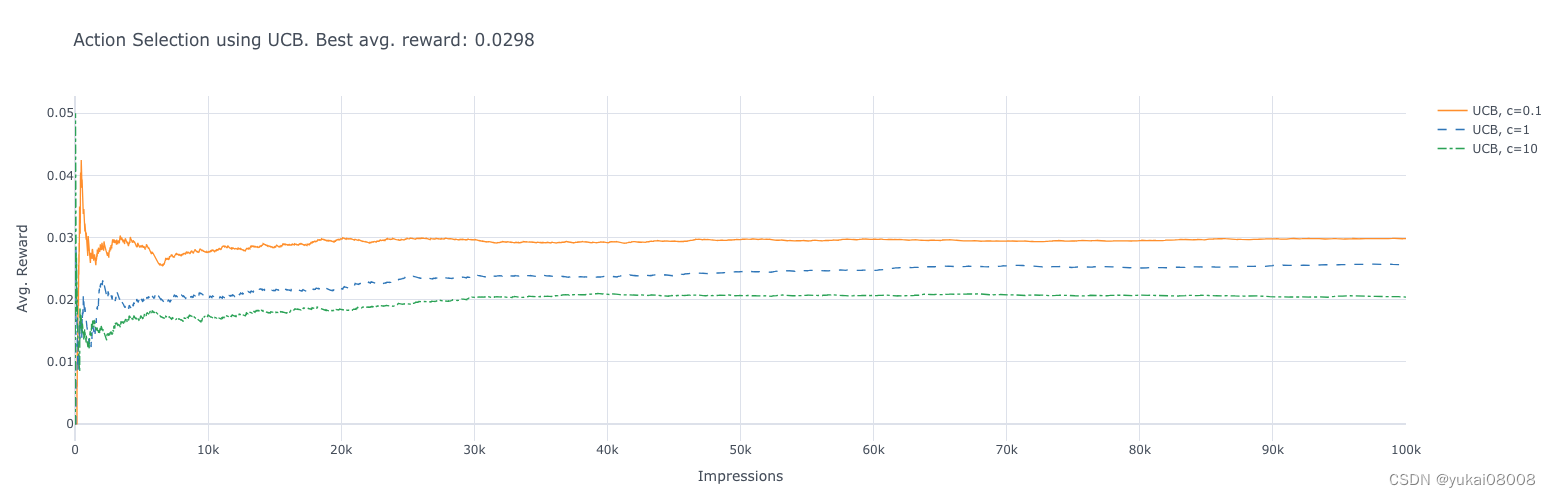
avg_rewards = []for t in range(1, n_prod + 1):if any(N==0):ad_chosen = np.random.choice(ad_indices[N==0])else:uncertainty = np.sqrt(np.log(t) / N)ad_chosen = np.argmax(Q + c * uncertainty)R = ads[ad_chosen].display_ad()N[ad_chosen] += 1Q[ad_chosen] += (1 / N[ad_chosen]) * (R - Q[ad_chosen])total_reward += Ravg_reward_so_far = total_reward / tavg_rewards.append(avg_reward_so_far)df_reward_comparison['UCB, c={}'.format(c)] = avg_rewards
这段代码实现了上限置信区间(Upper Confidence Bound, UCB)算法。UCB算法通过平衡探索(Exploration)和利用(Exploitation)来选择动作。其中,参数c用于调整探索与利用之间的权衡。
这段代码中,c 参数用于控制探索的程度。较大的 c 值将会更加强调探索,而较小的 c 值则更加强调利用。
这段代码的逻辑如下:
如果有至少一个广告的点击次数为零,则在这些广告中随机选择一个。
否则,计算每个广告的置信区间上界,并选择置信区间上界最大的广告。
显示所选择的广告,并获取奖励。
更新所选广告的点击次数和平均奖励。
计算当前总奖励和平均奖励,将平均奖励添加到列表中。
将平均奖励列表添加到 DataFrame 中,命名为 ‘UCB, c={}’。
4 Next
Review一下这一章,然后找一个具体的实用样例来进行实测,最后发布为前后端微服务。
相关文章:

Python 运筹优化13 Thompson Sampling 解读
说明 这部分应该是Multi-Armed Bandit的最后一部分了。 内容 1 On Line Ads 这个实验,最初的目的就是为了选出最佳的广告。首先,通过伯努利分布,模拟了某个广告的有效率。在真实场景里,我们是无法知道那个广告更好的。可能在t…...
计算机毕业设计 | SpringBoot健身房管理系统(附源码)
1,项目背景 随着人们生活水平的提高和健康意识的增强,健身行业逐渐兴起并迅速发展。而现代化的健身房管理系统已经成为健身房发展的必备工具之一。传统的健身房管理方式已经无法满足现代化健身房的需求,需要一种更加高效、智能、安全的管理系…...
大模型LLM 结合联网搜索增强isou
参考: https://github.com/yokingma/search_with_ai 在线使用网址: https://isou.chat/ 安装github下载,运行docker compose 如果一直报下面错误: 解决方法https://github.com/yokingma/search_with_ai/pull/7 默认打开&a…...

软删除和硬删除的区别及实际应用
在处理数据存储时,删除操作是不可避免的一部分。然而,并非所有的删除都是相同的。在本篇博客中,我们将探讨软删除(Soft Delete)和硬删除(Hard Delete)的概念、它们之间的区别,以及如…...
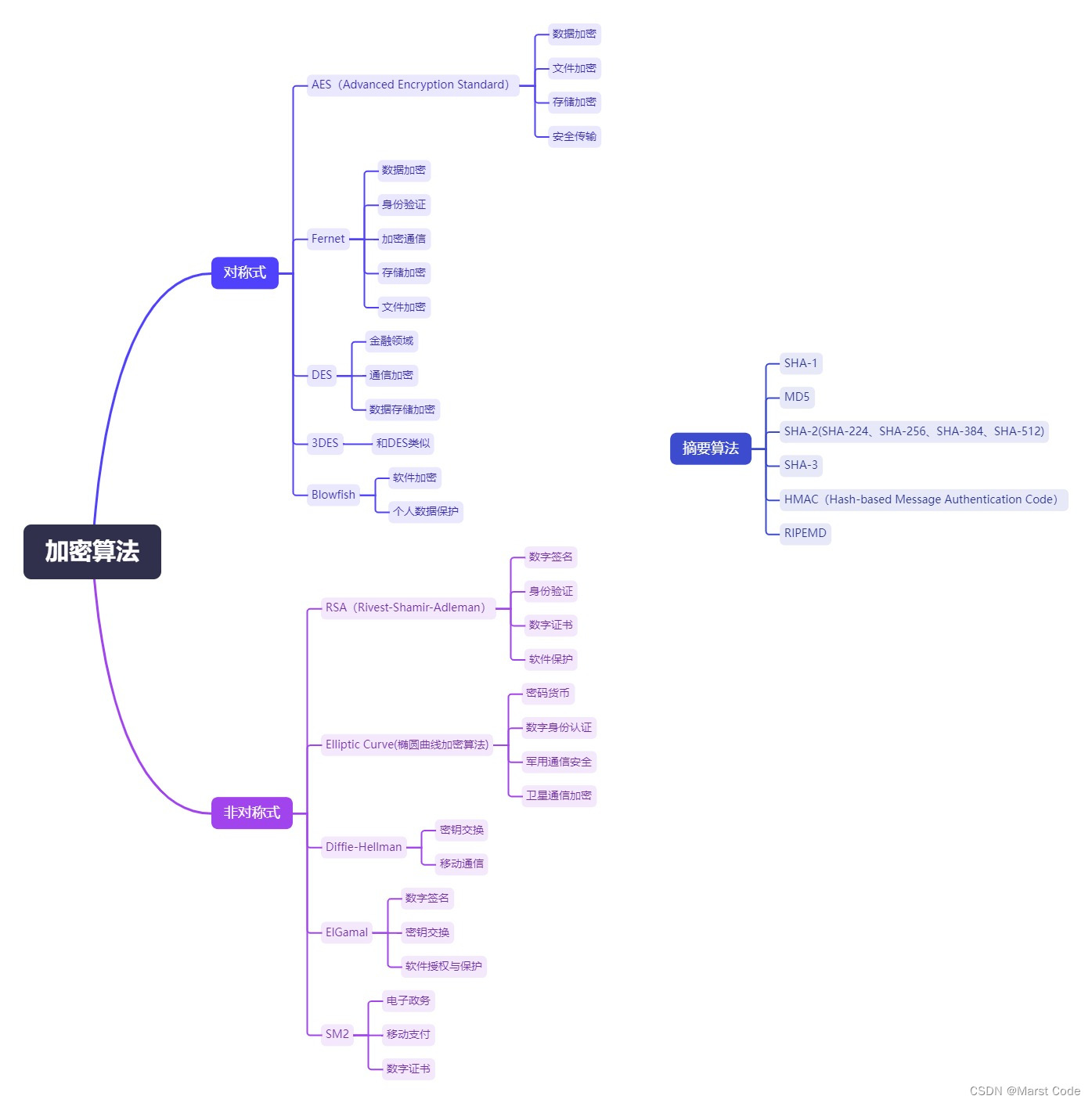
算法加密-简介
前言 在遥远的古代,信息的传递至关重要。战争时期,将领们需要确保自己的作战计划不被敌人知晓。 有一次,一位聪明的将军想要给远方的盟友传递一份机密战略部署。他想到了一个办法,用一种特殊的符号来替代文字。他和盟友事先约定好…...

搞懂Docker(九)- 使用Docker Compose
获取示例程序 示例程序 或者 示例程序 获取示例程序程序结构如下├── getting-started-app/ │ ├── package.json │ ├── README.md │ ├── spec/ │ ├── src/ │ └── yarn.lock使用Docker Compose Docker Compose是一个帮助你定义和共享多容器应用程序的工具…...

EOCRSP-40NM7施耐德电机保护器EOCR-SP
韩国三和EOCRSP-40NM7 40A AC220V电动机保护器 密集型设计 ■ 电子式多保护功能 ■ 宽的电流调整范围(10:1) ■ 电流表功能 ■ LED跳闸指示 ■ 高精度 ■ 手动即时复位 ■ 电动远距离复位 ■ 自检功能 ■ 强的环境适应性 ■ 低能耗 ■ 失效-安全工作方式(无电压释放) 韩国三和…...
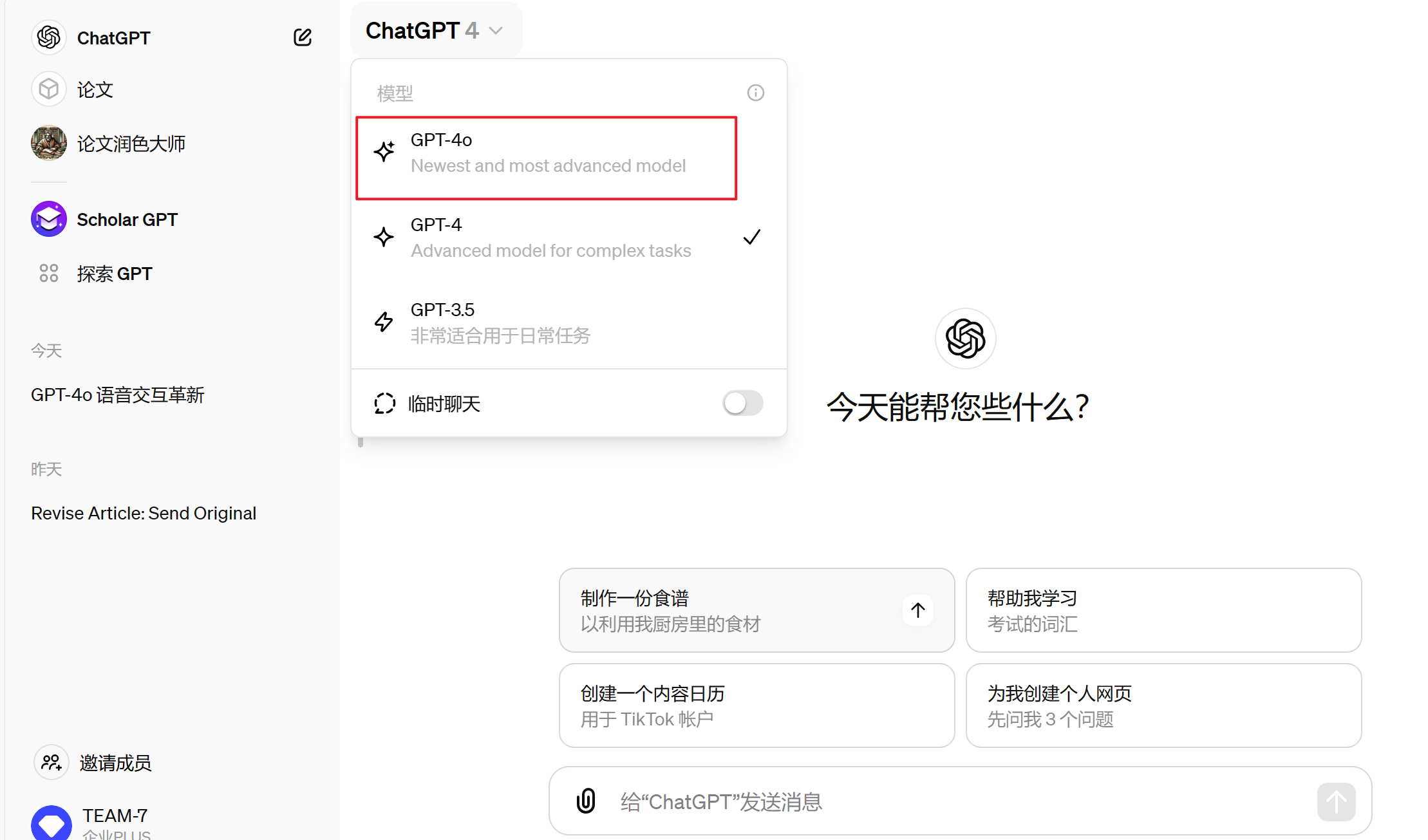
一文带你快速了解GPT-4o!内含免费使用指南!
一、GPT-4o简介 北京时间5月14日,OpenAI举行春季发布会。OpenAI在活动中发布了新旗舰模型“GPT-4o”!据OpenAI首席技术官穆里穆拉蒂(Muri Murati)介绍,GPT-4o在继承GPT-4强大智能的同时,进一步提升了文本、…...
)
react18【系列实用教程】useState (2024最新版)
类似 vue 的 data 选项 功能 向组件添加响应式变量,当响应式变量变化时,组件的视图UI也会跟着变化【数据驱动视图】 语法 参数为变量的初始值返回值为一个只有两个元素的数组,第一项元素为传入的参数,第二项元素是一个setter 函数…...

电商选品的数据是可以用爬虫进行采集的吗?
在电子商务领域,选品是一个至关重要的环节,它直接影响到商家的销售业绩和市场竞争力。为了做出更明智的选品决策,商家需要获取大量的市场数据和产品信息。那么,电商选品的数据是否可以通过爬虫进行采集呢? 爬虫在电商数…...
)
数据特征降维 | 局部线性嵌入(LLE)
局部线性嵌入(Locally Linear Embedding,LLE)是一种非线性降维和数据嵌入技术,用于将高维数据映射到低维空间中,以便更好地展示数据的结构和关系。 LLE的基本思想是假设数据样本在局部区域内可以近似由其相邻样本的线性组合表示。通过保持这种局部线性关系,LLE能够在低维…...

js发票查验、票据OCR接口助力解决发票录入与真假辨别难题
作为消费者,每位都是税法的监督员,为了保护自己的合法权益、共同维护市场秩序,消费者进行实际交易后无论是否需要报销,都应该主动向商家索取发票。一般来说发票主要有三种:增值税专用发票、普通发票、专业发票。以下&a…...

HTML静态网页成品作业(HTML+CSS+JS)——华为商城网页(1个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,使用Javacsript代码实现首页图片切换轮播效果,共有1个页面…...
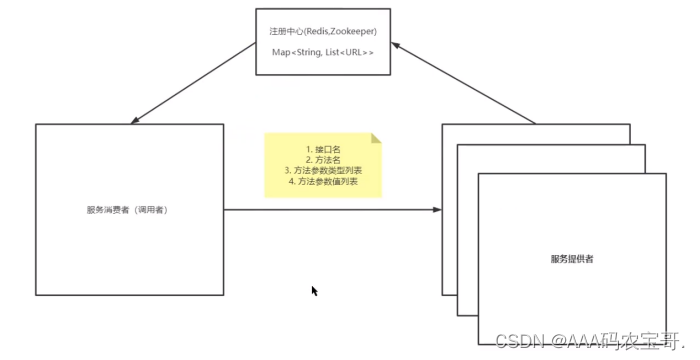
【吃透Java手写】5-RPC-简易版
【吃透Java手写】RPC-简易版-源码解析 1 RPC1.1 RPC概念1.2 常用RPC技术或框架1.3 初始工程1.3.1 Productor-common:HelloService1.3.2 Productor:HelloServiceImpl1.3.3 Consumer 2 模拟RPC2.1 Productor2.2 模拟一个RPC框架2.2.1 HttpServer2.2.2 Http…...

express 本地https服务 接口、静态文件,并支持跨域
var express require(express); var app express(); //设置跨域访问 app.all(*, function (req, res, next) {res.header(Access-Control-Allow-Origin, *);res.header(Access-Control-Allow-Credentials, true);res.header(Access-Control-Allow-Headers, Content-Type,Cont…...

从零手写实现 tomcat-08-tomcat 如何与 springboot 集成?
创作缘由 平时使用 tomcat 等 web 服务器不可谓不多,但是一直一知半解。 于是想着自己实现一个简单版本,学习一下 tomcat 的精髓。 系列教程 从零手写实现 apache Tomcat-01-入门介绍 从零手写实现 apache Tomcat-02-web.xml 入门详细介绍 从零手写…...
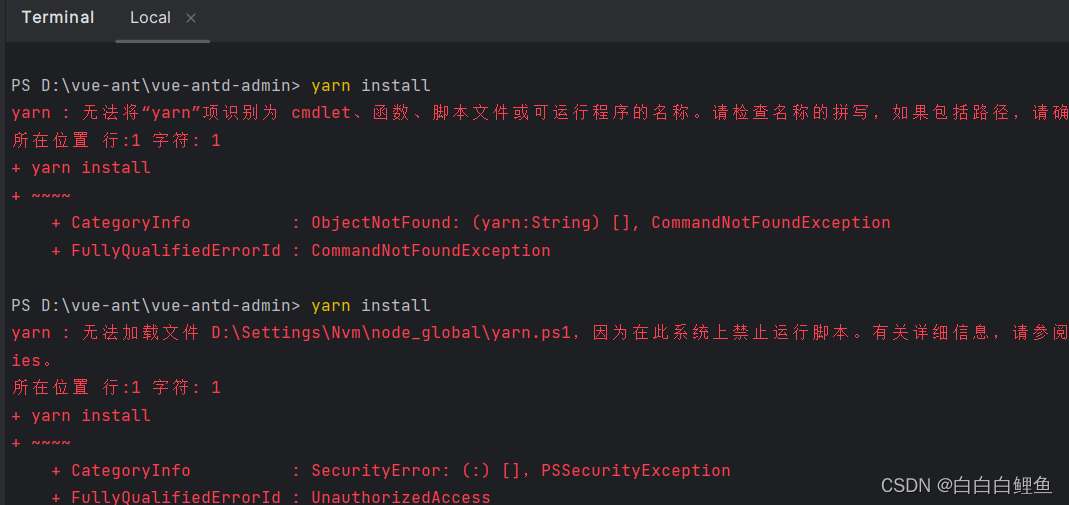
yarn 安装以及报错处理
前一种报错是由于没有安装yarn导致的,使用以下命令即可安装: npm install -g yarn 如果成功安装,将显示Yarn的版本号。 yarn --version 第二种报错是因为系统上的执行策略限制导致的。执行策略是一种安全功能,用于控制在计算机…...

31万奖金池等你挑战!IJCAI 2024 第九届“信也科技杯”全球AI算法大赛正式开赛!聚焦AI尖端赛题!
文章目录 ⭐️ 赛事概况⭐️ 赛事奖励⭐️ 赛事日程速览⭐️ 报名通道与赛事交流群⭐️ 关于 “信也科技杯”⭐️ 关于信也科技 ⭐️ 赛事概况 随着语音合成技术的不断进步,合成语音与真实语音之间的界限变得模糊,这不仅对数据安全构成威胁,也对科技伦理提出了新的要求。 第九…...

线性表—栈的实现
目录 栈的概念及结构 栈的实现 创建栈 栈的初始化 入栈 出栈 取出栈顶数据 判断栈是否为空 有效数据个数 栈的销毁 全代码 stack.h stack.c 应用 题目 示例 解题思路 代码实现 栈的概念及结构 栈是一种特殊的线性表,其只允许在固定的一端进行插入…...
react+antd --- 日期选择器,动态生成日期表格表头
先看一下效果---有当前月的日期 技术: 1: react 2:antd-UI库 -- table 3:moment--时间处理库 代码效果: import { Button, DatePicker, Table } from antd; import { useEffect, useState } from react; import momen…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
