【NOIP2008普及组复赛】 题4:立体图
题4:立体图
【题目描述】
小渊是个聪明的孩子,他经常会给周围的小朋友讲些自己认为有趣的内容。最近,他准备给小朋友讲解立体图,请你帮他画出立体图。
小渊有一块面积为mn的矩形区域,上面有mn个边长为1的格子,每个格子上堆了一些同样大小的积木(积木的长宽高都是1),小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式,并且不会做任何翻转旋转,只会严格以一种形式摆放。
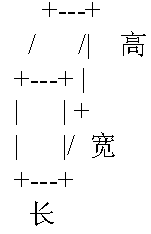
每个顶点用1个加号"+“表示,长用3个”-“表示,宽用1个”/“表示,高用两个”|“表示。符号”+“,”-“,”/“,”|“的ASCII码分别是43,45,47,124。字符”.“(ASCII码46)需要作为背景输出,即立体图中的空白部分需要用”."来代替。立体图的画法如下面的规则:
若两块积木左右相邻,图示为:
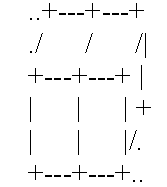
若两块积木上下相邻,图示为:
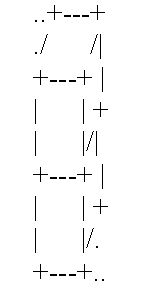
若两块积木前后相邻,图示为:
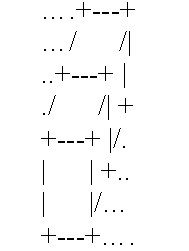
立体图中,定义位于第(m,1)的格子(即第m行第1列的格子)上面的自底向上的第一块积木(即最下面的一块积木)的左下角顶点为整张图最左下角的点。
【输入文件】
第一行有用空格隔开的2个整数m和n,表示有m*n个格子(1<=m,n<=50)。
接下来的m行,是一个m*n的矩阵,每行有n个用空格隔开的整数,其中第i行第j列上的整数表示第i行第j列的格子上摞有多少个积木(1<=每个格子上的积木数<=100)。
【输出文件】
包含题目要求的立体图,是一个K行L列的字符矩阵,其中K和L表示最少需要K行L列才能按规定输出立体图。
【输入样例1】
3 4
2 2 1 2
2 2 1 1
3 2 1 2
【输出样例1】

【代码如下】:
#include <bits/stdc++.h>
using namespace std;
char s[600][600];
void hua(int y, int x) {s[y][x] = '+';s[y][x + 1] = '-';s[y][x + 2] = '-';s[y][x + 3] = '-';s[y][x + 4] = '+';s[y + 1][x] = '|';s[y + 1][x + 1] = ' ';s[y + 1][x + 2] = ' ';s[y + 1][x + 3] = ' ';s[y + 1][x + 4] = '|';s[y + 1][x + 5] = '/';s[y + 2][x] = '|';s[y + 2][x + 1] = ' ';s[y + 2][x + 2] = ' ';s[y + 2][x + 3] = ' ';s[y + 2][x + 4] = '|';s[y + 2][x + 5] = ' ';s[y + 2][x + 6] = '+';s[y + 3][x] = '+';s[y + 3][x + 1] = '-';s[y + 3][x + 2] = '-';s[y + 3][x + 3] = '-';s[y + 3][x + 4] = '+';s[y + 3][x + 5] = ' ';s[y + 3][x + 6] = '|';s[y + 4][x + 1] = '/';s[y + 4][x + 2] = ' ';s[y + 4][x + 3] = ' ';s[y + 4][x + 4] = ' ';s[y + 4][x + 5] = '/';s[y + 4][x + 6] = '|';s[y + 5][x + 2] = '+';s[y + 5][x + 3] = '-';s[y + 5][x + 4] = '-';s[y + 5][x + 5] = '-';s[y + 5][x + 6] = '+';
}
int main(int argc, char *argv[]) {int a[55][55];int x1, y1, t, x, y;int i, j, k;int m, n;cin >> m >> n;x1 = 4 * n + 2 * m + 1;y1 = 0;for (i = 0; i < m; i++)for (j = 0; j < n; j++) {cin >> a[i][j];t = 3 * a[i][j] + 2 * (m - i) + 1;if (t > y1) y1 = t;}for (i = 0; i < y1; i++)for (j = 0; j < x1; j++) s[i][j] = '.';for (i = 0; i < m; i++)for (j = 0; j < n; j++)for (k = 0; k < a[i][j]; k++) {x = 2 * (m - i - 1) + 4 * j;y = 2 * (m - i - 1) + 3 * k;hua(y, x);}for (i = y1 - 1; i >= 0; i--) {for (j = 0; j < x1; j++) cout << s[i][j];if (i > 0) {cout << endl;}}return 0;
}
相关文章:

【NOIP2008普及组复赛】 题4:立体图
题4:立体图 【题目描述】 小渊是个聪明的孩子,他经常会给周围的小朋友讲些自己认为有趣的内容。最近,他准备给小朋友讲解立体图,请你帮他画出立体图。 小渊有一块面积为mn的矩形区域,上面有mn个边长为1的格子&#…...

【Leetcode每日一题】 动态规划 - 简单多状态 dp 问题 - 删除并获得点数(难度⭐⭐)(76)
1. 题目解析 题目链接:LCR 091. 粉刷房子 这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。 2.算法原理 1. 状态定义 在解决这类问题时,我们首先需要根据题目的具体要求来定义状态。针对房屋粉刷问题&#…...

Windows---CMD常用指令大全
CMD是什么? Windows操作系统中的命令行界面程序,全称为命令提示符 CMD可以干什么? 允许用户在文本界面下输入命令来执行各种操作,如文件管理、系统设置、软件安装等 帮助用户更好地控制和管理Windows系统 windows系统CMD指…...
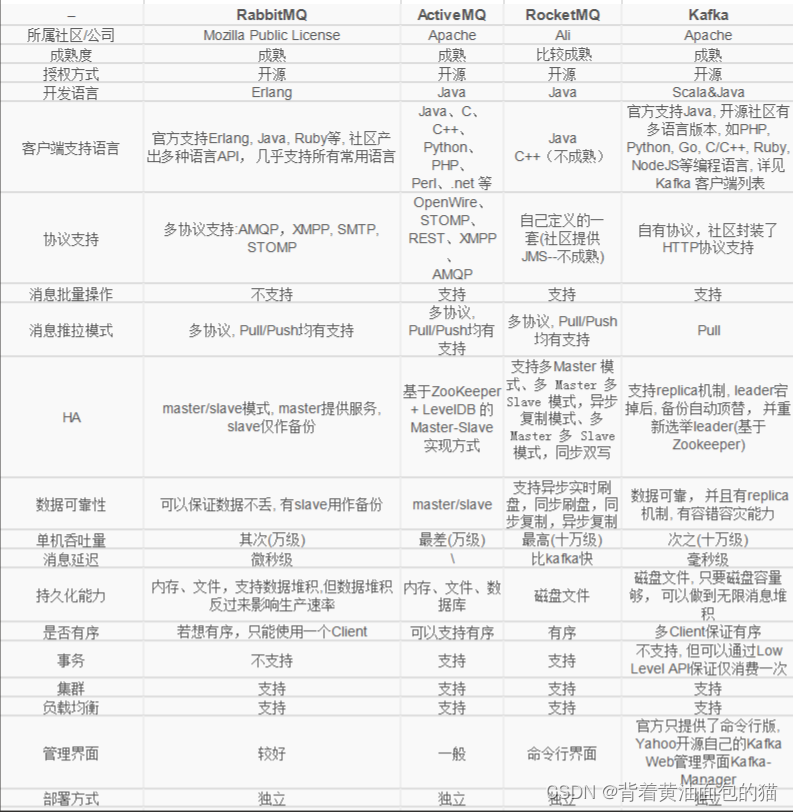
消息中间件是什么?有什么用?常见的消息中间件有哪些?
1.什么是消息中间件? 消息中间件基于队列模型在网络环境中为应用系统提供同步或异步、可靠的消息传输的支撑性软件系统。 2.现实中的痛点: 1.Http请求基于请求与响应的模型,在高并发的情况下,客户端发送大量的请求达到服务器端…...

富锂锰基材料极具发展潜力 我国产业化进程加速
富锂锰基材料极具发展潜力 我国产业化进程加速 富锂锰基材料以锰元素为主,我国锰资源较丰富,相比于铁锂材料、高镍三元材料,富锂锰基材料具有一定的降本潜力。此外富锂锰基材料在能量密度、充放电倍率等方面也具有明显优势。富锂锰基材料是富…...

聚水潭和金蝶云星空单据接口对接
聚水潭和金蝶云星空单据接口对接 对接系统:金蝶云星空 金蝶K/3Cloud(金蝶云星空)是移动互联网时代的新型ERP,是基于WEB2.0与云技术的新时代企业管理服务平台。金蝶K/3Cloud围绕着“生态、人人、体验”,旨在帮助企业打造…...

OpenAI深夜震撼发布最新模型GPT-4o,送上最快速便捷教程
北京时间5月14日凌晨,有人说OpenAI一夜改变了历史。 在我们的深夜、太平洋时间的上午 10 点,OpenAI 召开春季发布会,公布了最新的GPT-4o模型,o代表Omnimodel(全能模型)。20多分钟的演示直播,展…...
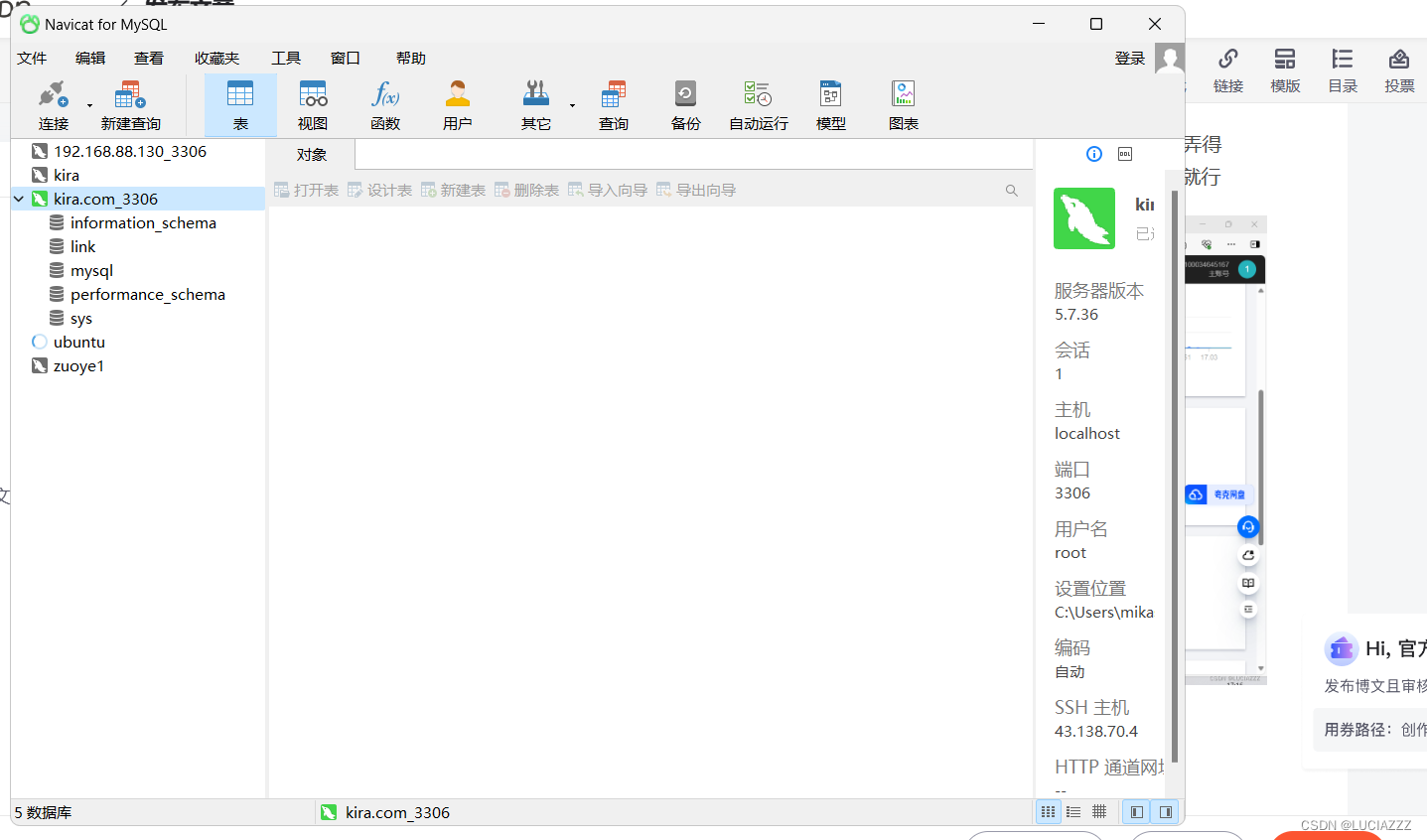
没有申请域名的情况下,用navicat远程连接我们的服务器的Mysql数据库
我们可以根据公网ip用shell来远程连接 首先我们打开自己买的服务器 例如你看这个,就是我们的公网IP 如果服务器里面没有安装mysql数据库的话,那么我们可以用一个轻量级的docker来安装数据库代替一下 我们用docker弄个轻量级的mysql5.7.36,…...

Hive中小文件过多的几种处理方式
1、使用concatenate(只支持RCFile和ORC格式) 2、减少map数量,调整参数:输入合并文件相关的参数 3、减少reduce的数量(例如直接设置reduce为xx个、或者设置reduce的大小,系统自动根据大小确定reduce的个数…...

用户登录认证和权限授权(SpringSecurity、JWT、session)
文章目录 前言一、登录认证1. 问题引入2. Session2.1 实现原理2.2 过滤器Filter2.3 上下文对象 3. JWT3.2 实现步骤3.3 拦截器 HandlerInterceptorAdapter3.4 上下文对象 4. Session VS JWT 二、权限授权1. 权限类型1.1 页面权限(菜单项权限)1.2 ACL模型…...
第十二届蓝桥杯省赛真题 Java A 组【原卷】
文章目录 发现宝藏【考生须知】试题 A: 相乘试题 B: 直线试题 C : \mathrm{C}: C: 货物摆放试题 D: 路径试题 E: 回路计数试题 F : \mathrm{F}: F: 最少砝码试题 G: 左孩子右兄弟试题 H : \mathrm{H}: H: 异或数列试题 I \mathbf{I} I 双向排序试题 J : \mathrm{J}: J: 分…...

工作随机:linux 挂载LVM管理模式的磁盘
文章目录 前言一、创建一个分区二、创建PV三、创建VG四、创建LV五、格式化并挂载目录 前言 在数据库管理中,常有比较头疼的问题,就是一段时间发展后我的磁盘空间不够了,想要扩容原有的目录很是头疼,那么LVM管理的优势就体现出来了…...

打印kafka最近的消息
使用 kafka-run-class 指令,获取topic的最小offset和最大offset #查看各个分区的最小offset(这个意思就是,这个offset之前的消息已经被清除了,现在consumer是从这个offset之后开始消费): ./kafka-run-class.sh kafka.tools.GetOffsetShell …...
e行64位V11.17.4 安卓全局虚拟定位APP
e行最新版11.17.4 支持全局虚拟位置 小米手机 百度地图 高德地图 实测成功 其他app自测 不一定支持所有app 下载:https://www.123pan.com/s/HAf9-tsyCh.html...

vue项目通过点击文字上传html文件,查看html文件
上传html文件 解决思路:新建一个上传组件,将它挪到页面之外。当点击文字时,手动触发上传组件,打开上传文件框。 <template><BasicTable register"registerTable"><template #bodyCell"{ column, …...

【WEEK12】 【DAY1】整合JDBC【中文版】
2024.5.13 Monday 目录 11.整合JDBC11.1.SpringData简介11.2.新建springboot-04-data项目11.3.新建application.yaml11.4.连接数据库11.5.修改Springboot04DataApplicationTests.java11.5.1.查看DataSourceProperties.java和DataSourceAutoConfiguration.java 11.6.JDBCTempla…...
)
23种设计模式(软考中级 软件设计师)
设计模式 23个设计模式,23个意图 1. 设计模式概要 设计模式的核心在于提供了相关问题的解决方案,使得人们可以更加简单方便的复用成功的设计和体系结构 设计模式的类别 创建型结构型行为型类工厂方法模式适配器模式(类)解释器模…...

记录一下 log4j的漏洞
目录 背景 bug的产生 bug复现 JNDI 网络安全学习路线 (2024最新整理) 学习资料的推荐 1.视频教程 2.SRC技术文档&PDF书籍 3.大厂面试题 特别声明: 背景 log4j这次的bug,我相信大家都已经知道了,仅以…...

Springboot-配置文件中敏感信息的加密:三种加密保护方法比较
一. 背景 当我们将项目部署到服务器上时,一般会在jar包的同级目录下加上application.yml配置文件,这样可以在不重新换包的情况下修改配置。 一般会将数据库连接、Redis连接等放到配置文件中。 例如配置数据库连接: spring:servlet:multip…...
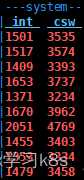
linux 性能监控命令之dstat
1. dstat 系统默认为安装,直接安装阿里源后,yum install -y dstat安装即可,该命令整合了 vmstat , iostat 和 ifstat,我们先看下效果: 我们先看看具体参数: [rootk8s-master ~]# dstat --help …...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
