三维人脸实践:基于Face3D的渲染、生成与重构 <二>
face3d: Python tools for processing 3D face
git code: https://github.com/yfeng95/face3d
paper list: PaperWithCode
3DMM方法,基于平均人脸模型,可广泛用于基于关键点的人脸生成、位姿检测以及渲染等,能够快速实现人脸建模与渲染。推荐!!!
目录
- face3d: Python tools for processing 3D face
- 一、介绍
- 1.1 3DMM定义
- 1.2 3dmm代码解读
- 1.2.0 加载相关库
- 1.2.1 加载处理过的BFM模型
- 1.2.2 生成人脸网格:顶点(形状)和颜色(纹理)
- 1.2.3 网格变换到合适的位置
- 1.2.4 将3D对象渲染为2d图像
- 二 反向过程
- 2.1 目标估计
- 2.2 2d和3d特征点转化
- 2.3 最小能量方程
- 2.3.1 代码解读
- 2.4 参数估计s,R,t2ds, R, t_{2d}s,R,t2d
- 2.4.1 黄金标准算法
- 总结
3DMM模型生成的人脸1:平常表情

3DMM模型生成的人脸2:微笑表情

3DMM模型是如何运行的?其原理是怎样的?如何实现三维人脸定制生成呢?
要回答上述问题,必须要弄清楚3DMM提供了哪些信息?如何编辑这些信息以达到特定的人脸生成。
一、介绍
在系列<一>中介绍了使用generate.m文件来产生BFM模型,具体包含BFM.mat,BFM_info.mat,BFM_UV.mat等。
1 BFM格式
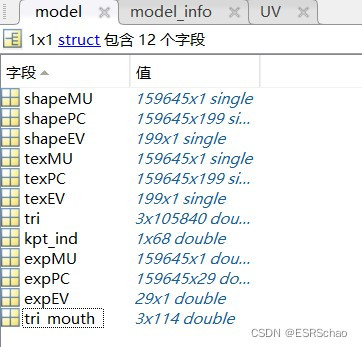
2 BFM_info格式

3 BFM_UV格式
这个matlab程序实现什么目的,从原理方面进行如下分析:
1.1 3DMM定义
3DMM公式如下:
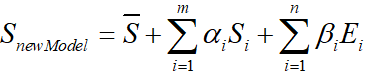
- Z^\hat{Z}Z^表示平均人脸形状
- SiS_iSi表示形状PCA主成分
- αi\alpha_iαi表示形状系数
- EiE_iEi表示人脸表情PCA主成分
- βi\beta_iβi表示人脸表情系数
BFM模型不提供原始人脸数据或参数化后的人脸,只提供形状和纹理信息。在BFM模型经过去中心化的数据所对应的m、n均为199。
01_MorphableModel.mat中具体包含数据如下
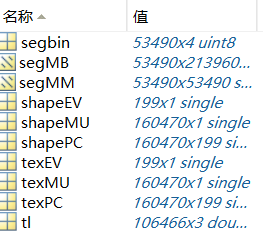
如下表所示:
| 名称 | 含义 | 维度 |
|---|---|---|
| shapeMU | 平均人脸形状 | (160470,1) |
| shapePC | 形状主成分 | (160470,199) |
| shapeEV | 形状主成分方差 | (199,1) |
| texMU | 平均人脸纹理 | (160470,1) |
| texPC | 纹理主成分 | (160470,199) |
| texEV | 纹理主成分方差 | (199,1) |
| tl | 三角面片 | (106466,3) |
| segbin | 区域分割信息 | (53490,4) |
1.2 3dmm代码解读
这里实现的是:
- 正向过程:从3dmm参数到mesh数据
- 反向过程:拟合,从2d图像和3dmm,生成3d face
1.2.0 加载相关库
''' 3d morphable model example
3dmm parameters --> mesh
fitting: 2d image + 3dmm -> 3d face
'''
import os, sys
import subprocess
import numpy as np
import scipy.io as sio
from skimage import io
from time import time
import matplotlib.pyplot as pltsys.path.append('..')
import face3d
from face3d import mesh
from face3d.morphable_model import MorphabelModel
1.2.1 加载处理过的BFM模型
# --------------------- Forward: parameters(shape, expression, pose) --> 3D obj --> 2D image ---------------
# --- 1. load model
bfm = MorphabelModel('Data/BFM/Out/BFM.mat')
print('init bfm model success')
其中,MorphabelModel所对应的源码为
class MorphabelModel(object):"""docstring for MorphabelModelmodel: nver: number of vertices. ntri: number of triangles. *: must have. ~: can generate ones array for place holder.'shapeMU': [3*nver, 1]. *'shapePC': [3*nver, n_shape_para]. *'shapeEV': [n_shape_para, 1]. ~'expMU': [3*nver, 1]. ~ 'expPC': [3*nver, n_exp_para]. ~'expEV': [n_exp_para, 1]. ~'texMU': [3*nver, 1]. ~'texPC': [3*nver, n_tex_para]. ~'texEV': [n_tex_para, 1]. ~'tri': [ntri, 3] (start from 1, should sub 1 in python and c++). *'tri_mouth': [114, 3] (start from 1, as a supplement to mouth triangles). ~'kpt_ind': [68,] (start from 1). ~"""def __init__(self, model_path, model_type = 'BFM'):super( MorphabelModel, self).__init__()if model_type=='BFM':self.model = load.load_BFM(model_path)else:print('sorry, not support other 3DMM model now')exit()# fixed attributesself.nver = self.model['shapePC'].shape[0]/3self.ntri = self.model['tri'].shape[0]self.n_shape_para = self.model['shapePC'].shape[1]self.n_exp_para = self.model['expPC'].shape[1]self.n_tex_para = self.model['texPC'].shape[1]self.kpt_ind = self.model['kpt_ind']self.triangles = self.model
['tri']self.full_triangles = np.vstack((self.model['tri'], self.model['tri_mouth']))
其中,self.model = load.load_BFM(model_path)所读取的model包含的信息如下表所示:
| 名称 | 含义 | 格式 |
|---|---|---|
| shapeMU | 平均人脸形状 | (159645,1) |
| shapePC | 形状主成分 | (159645,199) |
| shapeEV | 形状主成分方差 | (199,1) |
| expMU | 平均人脸表情 | (159645,1) |
| expPC | 表情主成分 | (159645,29) |
| expEV | 表情主成分方差 | (29,1) |
| texMU | 平均人脸纹理 | (159645,1) |
| texPC | 纹理主成分 | (159645,199) |
| texEV | 纹理主成分方差 | (199,1) |
| tri | 三角格坐标 | (105840,3) |
| tri_mouth | 嘴部三角格坐标 | (114,3) |
| kpt_ind | 特征点 | (68,) |
1.2.2 生成人脸网格:顶点(形状)和颜色(纹理)
这里采用随机的形状系数和表情系数
# --- 2. generate face mesh: vertices(represent shape) & colors(represent texture)
sp = bfm.get_shape_para('random')
ep = bfm.get_exp_para('random')
vertices = bfm.generate_vertices(sp, ep)tp = bfm.get_tex_para('random')
colors = bfm.generate_colors(tp)
colors = np.minimum(np.maximum(colors, 0), 1)
sp对应形状系数α\alphaα,ep对应表情系数β\betaβ,tptptp对应的是纹理系数。这些系数均随机产生。其中调用函数定义如下:
def get_shape_para(self, type = 'random'):if type == 'zero':sp = np.zeros((self.n_shape_para, 1))elif type == 'random':sp = np.random.rand(self.n_shape_para, 1)*1e04return spdef get_exp_para(self, type = 'random'):if type == 'zero':ep = np.zeros((self.n_exp_para, 1))elif type == 'random':ep = -1.5 + 3*np.random.random([self.n_exp_para, 1])ep[6:, 0] = 0return ep def generate_vertices(self, shape_para, exp_para):'''Args:shape_para: (n_shape_para, 1)exp_para: (n_exp_para, 1) Returns:vertices: (nver, 3)'''vertices = self.model['shapeMU'] + \self.model['shapePC'].dot(shape_para) + \self.model['expPC'].dot(exp_para)vertices = np.reshape(vertices, [int(3), int(len(vertices)/3)], 'F').Treturn vertices# -------------------------------------- texture: here represented with rgb value(colors) in vertices.def get_tex_para(self, type = 'random'):if type == 'zero':tp = np.zeros((self.n_tex_para, 1))elif type == 'random':tp = np.random.rand(self.n_tex_para, 1)return tpdef generate_colors(self, tex_para):'''Args:tex_para: (n_tex_para, 1)Returns:colors: (nver, 3)'''colors = self.model['texMU'] + self.model['texPC'].dot(tex_para)colors = np.reshape(colors, [int(3), int(len(colors)/3)], 'F').T/255. return colors
不难发现,顶点即形状主要使用shape和expression信息。纹理部分也采用类似原理计算。到此,新的人脸模型产生。
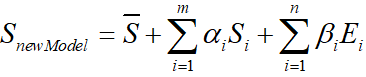
这里通过改变α\alphaα和β\betaβ系数,确实可以生成不同表情和形状的人脸数据,如开头展示的两组人脸图像。
1.2.3 网格变换到合适的位置
该部分在系列一中介绍过,给入尺度、旋转角度和平移坐标,即可得到变换后的位置。
# --- 3. transform vertices to proper position
s = 8e-04
angles = [10, 30, 20]
t = [0, 0, 0]
transformed_vertices = bfm.transform(vertices, s, angles, t)
projected_vertices = transformed_vertices.copy() # using stantard camera & orth projection
1.2.4 将3D对象渲染为2d图像
同pipeline中介绍雷同,给定生成图像宽高。
# --- 4. render(3d obj --> 2d image)
# set prop of rendering
h = w = 256; c = 3
image_vertices = mesh.transform.to_image(projected_vertices, h, w)
image = mesh.render.render_colors(image_vertices, bfm.triangles, colors, h, w)
#可使用如下代码将渲染后的二维图像可视化
plt.imshow(image)
plt.show()
以上部分实现的前向过程,即给出参数(形状,表情,姿态),生产三维对象,再转化为平面图。
Forward: parameters(shape, expression, pose) --> 3D obj --> 2D image
二 反向过程
参考:https://blog.csdn.net/likewind1993/article/details/81455882
从下定义可知,在使用3DMM进行人脸建模的时候,最大的问题就是shape和expression系数的确定。但论文里的介绍通常一笔带过,这里借助源码来充分理解。
2.1 目标估计
3DMM最早出现于99年的一篇文章:https://blog.csdn.net/likewind1993/article/details/79177566,论文里提出了一种人脸的线性表示方法。该方法可以通过以下实现:
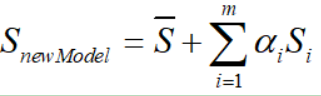
(原文中还加入了纹理部分,但是拟合效果不够好,一般直接从照片中提取纹理进行贴合,因此这里只给出重建人脸形状的部分)。
在2014年, FacewareHouse论文公开了一个人脸表情数据库,使得3DMM得到更多肯定,其将人脸模型的线性表示扩展为:
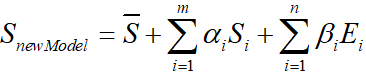
即在原文的基础上加入了Expression表情信息。
于是,人脸重建问题转为了求解α\alphaα和β\betaβ系数的问题。
2.2 2d和3d特征点转化
假设一张人脸照片,首先利用人脸对齐算法计算得到目标二维人脸的68个特征点坐标XXX,在BFM模型中有对应的68个特征点X3dX_{3d}X3d,根据这些信息便可求出α\alphaα和β\betaβ系数,将平均人脸模型与照片中的脸部进行拟合。投影后忽略第三维,其特征点之间的对应关系如下:
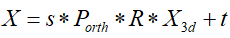
因此,可以根据以上将BFM中的三维模型投影到二维平面,即有:
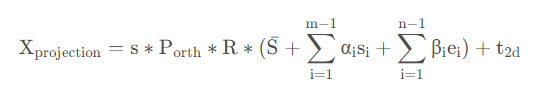
其中,XprojectionX_{projection}Xprojection是三维映射到二维平面的点,PorthP_{orth}Porth=[[1,0,0],[0,1,0]]为正交投影矩阵,R(3,3)为旋转矩阵,t2dt_{2d}t2d为位移矩阵。
2.3 最小能量方程
该问题可以转化为求解满足以下能量方程的系数(s,R,t2d,α,βs, R, t_{2d}, \alpha, \betas,R,t2d,α,β)
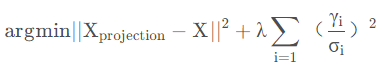
这里加入了正则化项,其中γ\gammaγ 是PCA系数(包含形状系数α\alphaα和表情系数β\betaβ),σ\sigmaσ表示对应的主成分偏差。
即,由上式求解使得三维模型中的68特征点投影到二维平面上的值与二维平面原68个特征点距离相差最小的系数。
这里继续讨论,如何给出详细的求解过程。
我们需要求得的参数主要有s,R,t2d,α,βs, R, t_{2d}, \alpha, \betas,R,t2d,α,β,这里可以把参数分为三个部分,s,R,t2ds, R, t_{2d}s,R,t2d,α\alphaα和β\betaβ
求解方法如下:
- 将α以及β初始化为0
- 求出 s,R,t2ds, R, t_{2d}s,R,t2d
- 将上一步求出的s,R,t2ds, R, t_{2d}s,R,t2d代入,求出α
- 将之前求出的s,R,t2ds, R, t_{2d}s,R,t2d以及α代入,求出β
- 利用求得的α以及β,重复2-4步骤进行迭代
2.3.1 代码解读
# -------------------- Back: 2D image points and corresponding 3D vertex indices--> parameters(pose, shape, expression) ------
## only use 68 key points to fit
x = projected_vertices[bfm.kpt_ind, :2] # 2d keypoint, which can be detected from image
X_ind = bfm.kpt_ind # index of keypoints in 3DMM. fixed.# fit
fitted_sp, fitted_ep, fitted_s, fitted_angles, fitted_t = bfm.fit(x, X_ind, max_iter = 3)# verify fitted parameters
fitted_vertices = bfm.generate_vertices(fitted_sp, fitted_ep)
transformed_vertices = bfm.transform(fitted_vertices, fitted_s, fitted_angles, fitted_t)image_vertices = mesh.transform.to_image(transformed_vertices, h, w)
fitted_image = mesh.render.render_colors(image_vertices, bfm.triangles, colors, h, w)
其中,x就是公式中的二维特征点X,这里给出的二维特征点来自于BFM。XindX_{ind}Xind是BFM模型三维特征点的索引,并非坐标。
然后执行拟合部分:
fitted_sp, fitted_ep, fitted_s, fitted_angles, fitted_t = bfm.fit(x, X_ind, max_iter = 3
bfm.fit的定义如下:
def fit(self, x, X_ind, max_iter = 4, isShow = False):''' fit 3dmm & pose parametersArgs:x: (n, 2) image pointsX_ind: (n,) corresponding Model vertex indicesmax_iter: iterationisShow: whether to reserve middle results for showReturns:fitted_sp: (n_sp, 1). shape parametersfitted_ep: (n_ep, 1). exp parameterss, angles, t'''if isShow:fitted_sp, fitted_ep, s, R, t = fit.fit_points_for_show(x, X_ind, self.model, n_sp = self.n_shape_para, n_ep = self.n_exp_para, max_iter = max_iter)angles = np.zeros((R.shape[0], 3))for i in range(R.shape[0]):angles[i] = mesh.transform.matrix2angle(R[i])else:fitted_sp, fitted_ep, s, R, t = fit.fit_points(x, X_ind, self.model, n_sp = self.n_shape_para, n_ep = self.n_exp_para, max_iter = max_iter)angles = mesh.transform.matrix2angle(R)return fitted_sp, fitted_ep, s, angles, t
这里执行了fit_points和matrix2angle函数,其定义分别有:
def fit_points(x, X_ind, model, n_sp, n_ep, max_iter = 4):'''Args:x: (n, 2) image pointsX_ind: (n,) corresponding Model vertex indicesmodel: 3DMMmax_iter: iterationReturns:sp: (n_sp, 1). shape parametersep: (n_ep, 1). exp parameterss, R, t'''x = x.copy().T#-- initsp = np.zeros((n_sp, 1), dtype = np.float32)ep = np.zeros((n_ep, 1), dtype = np.float32)#-------------------- estimateX_ind_all = np.tile(X_ind[np.newaxis, :], [3, 1])*3X_ind_all[1, :] += 1X_ind_all[2, :] += 2valid_ind = X_ind_all.flatten('F')shapeMU = model['shapeMU'][valid_ind, :]shapePC = model['shapePC'][valid_ind, :n_sp]expPC = model['expPC'][valid_ind, :n_ep]for i in range(max_iter):X = shapeMU + shapePC.dot(sp) + expPC.dot(ep)X = np.reshape(X, [int(len(X)/3), 3]).T#----- estimate poseP = mesh.transform.estimate_affine_matrix_3d22d(X.T, x.T)s, R, t = mesh.transform.P2sRt(P)rx, ry, rz = mesh.transform.matrix2angle(R)# print('Iter:{}; estimated pose: s {}, rx {}, ry {}, rz {}, t1 {}, t2 {}'.format(i, s, rx, ry, rz, t[0], t[1]))#----- estimate shape# expressionshape = shapePC.dot(sp)shape = np.reshape(shape, [int(len(shape)/3), 3]).Tep = estimate_expression(x, shapeMU, expPC, model['expEV'][:n_ep,:], shape, s, R, t[:2], lamb = 0.002)# shapeexpression = expPC.dot(ep)expression = np.reshape(expression, [int(len(expression)/3), 3]).Tsp = estimate_shape(x, shapeMU, shapePC, model['shapeEV'][:n_sp,:], expression, s, R, t[:2], lamb = 0.004)return sp, ep, s, R, t
fit.fit_points部分拆分讲解
(1)初始化α , β为0
x = x.copy().T#-- initsp = np.zeros((n_sp, 1), dtype = np.float32)ep = np.zeros((n_ep, 1), dtype = np.float32)
x取转置,格式变为(2,68)
sp即α,ep即β。将它们赋值为格式(199,1)的零向量。
X3dX_{3d}X3d进行坐标转换
由于BFM模型中的顶点坐标储存格式为x1,y1,z1,x2,y2,z2,...{x_1,y_1,z_1,x_2,y_2,z_2,...}x1,y1,z1,x2,y2,z2,...
而在X_ind中只给出了三位特征点坐标的位置,所以应该根据X_ind获取X3dX_{3d}X3d的XYZ坐标数据。
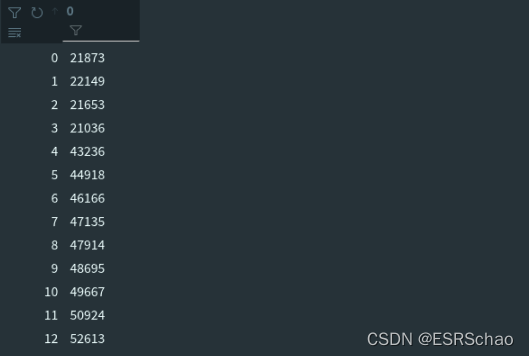
X_ind_all = np.tile(X_ind[np.newaxis, :], [3, 1])*3X_ind_all[1, :] += 1X_ind_all[2, :] += 2valid_ind = X_ind_all.flatten('F')
X_ind数据如下,是一个(68,1)的位置数据。
X_ind_all = np.tile(X_ind[np.newaxis, :], [3, 1])*3
X_ind_all拓展为(3,68)并乘3来定位到坐标位置:

X_ind_all[1, :] += 1
X_ind_all[2, :] += 2
再将第二行加一、第三行加二来对于Y坐标和Z坐标。

然后将它们拉伸为一维数组。flatten适用于numpy对应即array和mat,list不适用。
valid_ind = X_ind_all.flatten('F')
'F’表示以列优先展开。
合并后的结果valid_ind如下图:
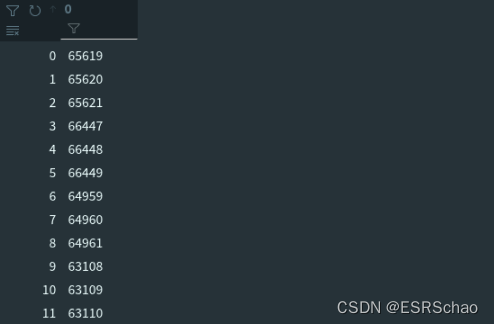
通过合并后的valid_ind得到对应特征点的人脸形状、形状主成分、表情主成分这三种数据。
shapeMU = model['shapeMU'][valid_ind, :]
shapePC = model['shapePC'][valid_ind, :n_sp]
expPC = model['expPC'][valid_ind, :n_ep]
人脸形状shapeMU数据格式(683,1)
形状主成分shapePC数据格式(683,199)
表情主成分expPC数据格式(68*3,29)
for i in range(max_iter):X = shapeMU + shapePC.dot(sp) + expPC.dot(ep)X = np.reshape(X, [int(len(X)/3), 3]).T#----- estimate poseP = mesh.transform.estimate_affine_matrix_3d22d(X.T, x.T)s, R, t = mesh.transform.P2sRt(P)rx, ry, rz = mesh.transform.matrix2angle(R)# print('Iter:{}; estimated pose: s {}, rx {}, ry {}, rz {}, t1 {}, t2 {}'.format(i, s, rx, ry, rz, t[0], t[1]))#----- estimate shape# expressionshape = shapePC.dot(sp)shape = np.reshape(shape, [int(len(shape)/3), 3]).Tep = estimate_expression(x, shapeMU, expPC, model['expEV'][:n_ep,:], shape, s, R, t[:2], lamb = 0.002)# shapeexpression = expPC.dot(ep)expression = np.reshape(expression, [int(len(expression)/3), 3]).Tsp = estimate_shape(x, shapeMU, shapePC, model['shapeEV'][:n_sp,:], expression, s, R, t[:2], lamb = 0.004)return sp, ep, s, R, t
循环中的max_iter是自行定义的迭代次数,这里的输入为4。
X = shapeMU + shapePC.dot(sp) + expPC.dot(ep)
X = np.reshape(X, [int(len(X)/3), 3]).T
这里的X就是经过如下的运算的SnewmodelS_{newmodel}Snewmodel,就是新的X3dX_{3d}X3d
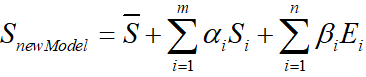
真正重点的是mesh.transform.estimate_affine_matrix_3d22d(X.T, x.T),这是网格的拟合部分。
源码如下:
estimate_affine_matrix_3d22d(X, x):''' Using Golden Standard Algorithm for estimating an affine cameramatrix P from world to image correspondences.See Alg.7.2. in MVGCV Code Ref: https://github.com/patrikhuber/eos/blob/master/include/eos/fitting/affine_camera_estimation.hppx_homo = X_homo.dot(P_Affine)Args:X: [n, 3]. corresponding 3d points(fixed)x: [n, 2]. n>=4. 2d points(moving). x = PXReturns:P_Affine: [3, 4]. Affine camera matrix'''X = X.T; x = x.Tassert(x.shape[1] == X.shape[1])n = x.shape[1]assert(n >= 4)#--- 1. normalization# 2d pointsmean = np.mean(x, 1) # (2,)x = x - np.tile(mean[:, np.newaxis], [1, n])average_norm = np.mean(np.sqrt(np.sum(x**2, 0)))scale = np.sqrt(2) / average_normx = scale * xT = np.zeros((3,3), dtype = np.float32)T[0, 0] = T[1, 1] = scaleT[:2, 2] = -mean*scaleT[2, 2] = 1# 3d pointsX_homo = np.vstack((X, np.ones((1, n))))mean = np.mean(X, 1) # (3,)X = X - np.tile(mean[:, np.newaxis], [1, n])m = X_homo[:3,:] - Xaverage_norm = np.mean(np.sqrt(np.sum(X**2, 0)))scale = np.sqrt(3) / average_normX = scale * XU = np.zeros((4,4), dtype = np.float32)U[0, 0] = U[1, 1] = U[2, 2] = scaleU[:3, 3] = -mean*scaleU[3, 3] = 1# --- 2. equationsA = np.zeros((n*2, 8), dtype = np.float32);X_homo = np.vstack((X, np.ones((1, n)))).TA[:n, :4] = X_homoA[n:, 4:] = X_homob = np.reshape(x, [-1, 1])# --- 3. solutionp_8 = np.linalg.pinv(A).dot(b)P = np.zeros((3, 4), dtype = np.float32)P[0, :] = p_8[:4, 0]P[1, :] = p_8[4:, 0]P[-1, -1] = 1# --- 4. denormalizationP_Affine = np.linalg.inv(T).dot(P.dot(U))return P_Affinedef P2sRt(P):''' decompositing camera matrix PArgs: P: (3, 4). Affine Camera Matrix.Returns:s: scale factor.R: (3, 3). rotation matrix.t: (3,). translation. '''t = P[:, 3]R1 = P[0:1, :3]R2 = P[1:2, :3]s = (np.linalg.norm(R1) + np.linalg.norm(R2))/2.0r1 = R1/np.linalg.norm(R1)r2 = R2/np.linalg.norm(R2)r3 = np.cross(r1, r2)R = np.concatenate((r1, r2, r3), 0)return s, R, t
(2)利用黄金标准算法得到一个仿射矩阵PAP_{A}PA,分解得到s,R,t2ds,R,t_{2d}s,R,t2d
2.4 参数估计s,R,t2ds, R, t_{2d}s,R,t2d
人脸模型中的三维点与对应照片中的二维点存在映射关系,可以用一个3×4的仿射矩阵进行表示。即:
X2d=P×X3dX_{2d} = P \times X_{3d}X2d=P×X3d
P即是我们需要求的仿射矩阵,作用在三维坐标点上可以得到二维坐标点。
这里使用黄金标准算法(Gold Standard Algorithm)来求该仿射矩阵,estimate_affine_matrix_3d22d部分即黄金标准算法具体过程
2.4.1 黄金标准算法
算法表述如下:
目标:在给定多组从3d到2d的图像对应集合(点对的数量>=4),确定仿射相机投影矩阵的最大似然估计。
- 归一化
对二维点XXX,计算一个相似变换TTT,使得X^=TX\hat{X}=TXX^=TX,同样的对于三维点X3dX_{3d}X3d,计算X^3d=UX3d\hat{X}_{3d}=UX_{3d}X^3d=UX3d。
归一化部分的概念在Multiple View Geometry in Computer Vision一书中描述如下:

所以归一化可以概述为以下三步:
- 平移所有坐标点,使它们的质心位于原点。
- 然后对这些点进行缩放,使到原点的平均距离等于2\sqrt{2}2 。
- 将该变换应用于图像中的每一幅。
下面结合代码进行讲解:
输入检测,确保输入的二维和三维特征点的数目一致以及特征点数目大于4。
X = X.T; x = x.Tassert(x.shape[1] == X.shape[1])n = x.shape[1]assert(n >= 4)
二维数据归一化:
#--- 1. normalization# 2d pointsmean = np.mean(x, 1) # (2,)x = x - np.tile(mean[:, np.newaxis], [1, n])average_norm = np.mean(np.sqrt(np.sum(x**2, 0)))scale = np.sqrt(2) / average_normx = scale * xT = np.zeros((3,3), dtype = np.float32)T[0, 0] = T[1, 1] = scaleT[:2, 2] = -mean*scaleT[2, 2] = 1
- 平移所有坐标点,使它们的质心位于原点。
经过x=x.T后x的格式变为(2,68)
通过mean = np.mean(x, 1)获取x的X坐标和Y坐标平均值mean,格式为(2,)
这一步x = x - np.tile(mean[:, np.newaxis], [1, n])
x的所有XY坐标都减去刚刚算出的平均值,此时x中的坐标点被平移到了质心位于原点的位置。 - 然后对这些点进行缩放,使到原点的平均距离等于2\sqrt{2}2 。
average_norm = np.mean(np.sqrt(np.sum(x**2, 0)))
算出所有此时所有二维点到原点的平均距离average_norm,这是一个数值。
scale = np.sqrt(2) / average_norm
x = scale * x
算出scale再用scale去乘x坐标,相当与x所有的坐标除以当前的平均距离之后乘以2\sqrt{2}2
这样算出来的所有点到原点的平均距离就被缩放到了$\sqrt{2}¥ - 同时通过计算出的scale和mean可以算出相似变换T
T = np.zeros((3,3), dtype = np.float32)
T[0, 0] = T[1, 1] = scale
T[:2, 2] = -mean*scale
T[2, 2] = 1
# 3d pointsX_homo = np.vstack((X, np.ones((1, n))))mean = np.mean(X, 1) # (3,)X = X - np.tile(mean[:, np.newaxis], [1, n])m = X_homo[:3,:] - Xaverage_norm = np.mean(np.sqrt(np.sum(X**2, 0)))scale = np.sqrt(3) / average_normX = scale * XU = np.zeros((4,4), dtype = np.float32)U[0, 0] = U[1, 1] = U[2, 2] = scaleU[:3, 3] = -mean*scaleU[3, 3] = 1
三位归一化的原理与二维相似,区别就是所有点到原点的平均距离要被缩放到3\sqrt{3}3 ,以及生成的相似变换矩阵UUU格式为(4,4)。这不赘述了。
- 对于每组对应点xix_ixi~XiX_iXi,都有形如Ax=bAx=bAx=b 的对应关系存在
# --- 2. equationsA = np.zeros((n*2, 8), dtype = np.float32);X_homo = np.vstack((X, np.ones((1, n)))).TA[:n, :4] = X_homoA[n:, 4:] = X_homob = np.reshape(x, [-1, 1])
这里结合公式来看,
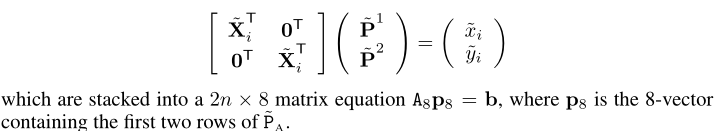
A对应其中的[X^iT0T0TXiT]\begin{bmatrix} \hat{X}^T_i & 0^T\\ 0^T & X^T_i \end{bmatrix}[X^iT0T0TXiT]
b是展开为(68*2,1)格式的x。
求出A的伪逆
# --- 3. solutionp_8 = np.linalg.pinv(A).dot(b)P = np.zeros((3, 4), dtype = np.float32)P[0, :] = p_8[:4, 0]P[1, :] = p_8[4:, 0]P[-1, -1] = 1
关于A的伪逆的概念和求取方法可以参照Multiple View Geometry in Computer Vision书中的P590以后的内容。这里A的伪逆是利用numpy里面的函数np.linalg.pinv直接计算出来的,非常方便。
去掉归一化,得到仿射矩阵
# --- 4. denormalizationP_Affine = np.linalg.inv(T).dot(P.dot(U))return P_Affine
这部分的代码参照公式:
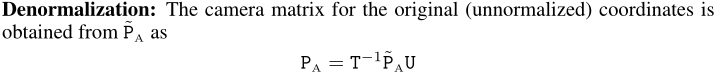
以上四步就是黄金标准算法的完整过程
得到的PAffineP_{Affine}PAffine就是式中的PAP_APA,到这里,我们通过黄金标准算法得到了X=PA⋅X3dX = P_A\cdot X_{3d}X=PA⋅X3d中的PAP_APA。
将仿射矩阵PAP_APA分解得到s,R,t2ds, R, t_{2d}s,R,t2d
s, R, t = mesh.transform.P2sRt(P)
rx, ry, rz = mesh.transform.matrix2angle(R)
其中mesh.transform.P2sRt部分的源码如下:
def P2sRt(P):''' decompositing camera matrix PArgs: P: (3, 4). Affine Camera Matrix.Returns:s: scale factor.R: (3, 3). rotation matrix.t: (3,). translation. '''t = P[:, 3]R1 = P[0:1, :3]R2 = P[1:2, :3]s = (np.linalg.norm(R1) + np.linalg.norm(R2))/2.0r1 = R1/np.linalg.norm(R1)r2 = R2/np.linalg.norm(R2)r3 = np.cross(r1, r2)R = np.concatenate((r1, r2, r3), 0)return s, R, t
这部分就是将仿射矩阵RA{R_A}RA分解为下图的缩放比例s、旋转矩阵R以及平移矩阵t
总结
这里主要介绍基于3DMM模型的前向与反向过程。前向过程,基于3DMM,给出参数的情况下,生产三维对象和二维人脸;反向过程,给出人脸关键点的情况下,估计形状和颜色参数等,形成对应的三维人脸建模。
相关文章:
三维人脸实践:基于Face3D的渲染、生成与重构 <二>
face3d: Python tools for processing 3D face git code: https://github.com/yfeng95/face3d paper list: PaperWithCode 3DMM方法,基于平均人脸模型,可广泛用于基于关键点的人脸生成、位姿检测以及渲染等,能够快速实现人脸建模与渲染。推…...
在linux上部署Java项目
在Linux部署Java环境 要是想要部署java web程序,首先要配置环境 jdk tomcat mysql 安装jdk 推荐的方法是使用yum直接安装openjdk(开源的,与官方的jdk功能差不多),目前使用的最多的就是jdk8系列 yum list | grep jdk 在源上搜索所有关于jdk的文件 devel表示development的意思…...

线性表的接口
线性表的实现方式 顺序表 顺序表是一种线性表的实现方式,它是用一组地址连续的存储单元依次存储线性表中的数据元素,使得逻辑上相邻的元素在物理上也相邻⁴。顺序表可以用数组来实现,它的优点是可以快速定位第几个元素,但是缺点…...

spark三种操作模式的不同点分析
通常情况下,由于mapreduce计算引擎的效率问题,大部分公司使用的基本都是hive数仓spark计算引擎的方式搭建集群,所以对于spark的三种操作方式来进行简单的分析。在日常开发中,使用最多的方式取决于具体的需求和场景。以下是每种方式的一些常见用途:Spark …...
Vue3做出B站【bilibili】 Vue3+TypeScript【快速入门一篇文章精通系列(一)前端项目案例】
本项目分为二部分 1、后台管理系统(用户管理,角色管理,视频管理等) 2、客户端(登录注册、发布视频) Vue3做出B站【bilibili】 Vue3TypeScript【快速入门一篇文章精通系列(一)前端项目…...
)
猜数游戏--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例10:猜数游戏 猜数游戏是一个古老的密码破译类、益智类小游戏,通常由两个人参与,一个人设置一个数字,一个人猜数字,当猜数字的人说出一个数字,由出数字的人告知是否猜中:若猜测的数字大于设…...

Nvidia jetson nano 部署yolov5_技术文档
Nvidia jetson nano 部署yolov5_技术文档 每天一句小姜格言:我行,我不是一般人儿 部署开始: 1、通过FileZilla,将window文件传输至jetson nano 上的nano文件夹下。 2、查看cuda 我买的jetson nano是带有配置好的镜像。系统配置…...

获取当前天数前N天
获取当前天数前N天 先封装到js里面 export const isTime (val) > {// 1.获取当前时间年月日时分秒格式xxxx-xx-xx xx:xx:xxvar myDate new Date() // 当前时间var y myDate.getFullYear() // 当前年份四位数var m myDate.getMonth() 1 < 10? 0 (myDate.getMont…...

Linux---基本指令
专栏:Linux 个人主页:HaiFan. 基本指令ls 指令pwd命令cd 指令touch指令mkdir指令(重要)rmdir指令 && rm 指令(重要)man指令(重要)cp指令(重要)mv指令…...
【UE4 RTS游戏】02-摄像机运动_完成摄像机在X轴上运动的相关步骤
效果通过控制键盘WS键使得“CameraPawn”进行前后移动步骤将landscape的Z轴位置更改为0删除“PostProcessVolume”将“LightmassImportanceVolume”移入Lighting文件夹内新建一个蓝图类,父类是Pawn,命名为“CameraPawn”将“MyController”重命名为“Cam…...
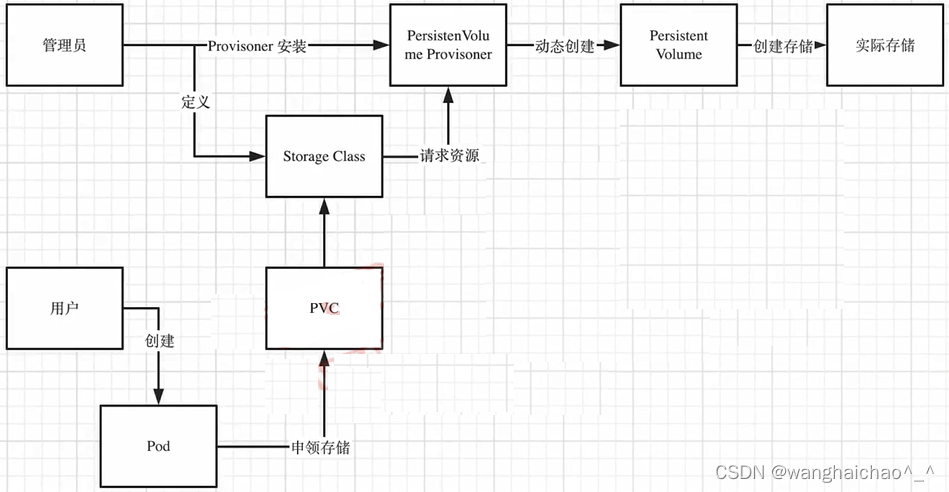
Kubernetes学习(五)持久化存储
Volume 卷 容器中的文件在磁盘上是临时存放的,这给容器中运行的特殊应用带来了一些问题。首先,当容器崩溃时,kubectl将重新启动容器,容器中的文件将会丢失--应为容器会以干净的状态重建。其次,当在一个Pod中运行多个容…...

下一个7年,保持期待、持续思考,酷雷曼继续向前!
过去7年,我们一直在思考, VR技术究竟能为我们的生活带来什么? 是足不出户就能云游千里的秀美风光? 是在家就能沉浸式体验线上消费的便利? 还是为商企和用户搭建更快速的沟通桥梁? NO.1、技术变革 在信…...

天梯赛训练L1-010--L1-012
目录 1、L1-010 比较大小 2、L1-011 A-B 3、L1-012 计算指数 4,一些题外话 1、L1-010 比较大小 分数 10 本题要求将输入的任意3个整数从小到大输出。 输入格式: 输入在一行中给出3个整数,其间以空格分隔。 输出格式: 在一…...
三分钟完成Stable Diffusion本地安装(零基础体验AI绘画)
三分钟完成Stable Diffusion本地安装前言安装步骤下载链接前言 最近AI绘画很火,很多无编程基础的小伙伴也想体验一下,所以写这篇博客来帮助小伙伴们愉快的体验一下~废话少说,我们直接开整! 安装步骤 首先,下载本项目的…...

电子台账:教程目录及软件下载
前面内容有点杂乱,这里整理一下教程目录。重点是制作模板,企业只要学会适合自己的一种就行。如果这些模板都学会做了,那可以当老师了。1 目录1 模板制作之一——列过滤(水平过滤)2 模板制作之二——行过滤(…...

多态的优势和弊端
目录 1.多态的优势 2.多态的弊端是什么? 3.引用数据类型的类型,转换有几种方式 4.强制类型转换能解决什么问题楠? 1.多态的优势 方法中,使用父类作为参数,可以接收所有子类的对象 package ploydemo3;import java.u…...

android h5考勤管理系统myeclipse开发mysql数据库编程服务端java计算机程序设计
一、源码特点 android h5考勤管理系统是一套完善的WEBandroid设计系统,对理解JSP java,安卓app编程开发语言有帮助(系统采用web服务端APP端 综合模式进行设计开发),系统具有完整的源代 码和数据库,系统主…...

第二道pwn题:shellcode
题目来自视频:链接:https://pan.baidu.com/s/17vX9dbfHkXBw71mcEXBgNQ?pwd6666 提取码:6666查看文件类型和保护,虽然现在的我还没有明白太多的保护。64位,放到ida里边rbp:保存的是栈中当前执行函数的基本地址。当前执…...

《华为数据之道》读书笔记
《华为数据之道》读书笔记第二章:2.2.1 管理总纲有四点:信息架构管理原则、数据产生管理、数据应用管理原则、数据问责与奖惩管理原则2.1.2 信息架构管理政策:管理信息架构的角色与职责:公司数据Owner、各数据Owner、数据管理专业…...
C++源码pcl1.13.0库编译环境搭建及配置
Pcl github库https://github.com/PointCloudLibrary/pcl官网地址https://pointclouds.org/Pcl exe的下载地址,各个版本,以及各版本对应的源码https://github.com/PointCloudLibrary/pcl/releases源码需要编译,编译之前安装AllInOne的exe程序&…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...
