【算法优选】 动态规划之子数组、子串系列——壹
文章目录
- 🎋前言
- 🎋最大子数组和
- 🚩题目描述
- 🚩算法思路
- 🚩代码实现
- 🌴环形子数组的最大和
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- 🌲乘积最大子数组
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- ⭕总结
🎋前言
动态规划相关题目都可以参考以下五个步骤进行解答:
-
状态表示
-
状态转移⽅程
-
初始化
-
填表顺序
-
返回值
后面题的解答思路也将按照这五个步骤进行讲解。
🎋最大子数组和
🚩题目描述
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
- 示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。 - 示例 2:
输入:nums = [1]
输出:1 - 示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
class Solution {public int maxSubArray(int[] nums) {}
}
🚩算法思路
- 状态表示:
对于线性 dp ,我们可以⽤「经验 + 题⽬要求」来定义状态表示:
- 以某个位置为结尾,进行一系列操作;
- 以某个位置为起点,进行一系列操作。
这⾥我们选择比较常用的方式,以「某个位置为结尾」,结合「题目要求」,定义⼀个状态表示:
dp[i] 表⽰:以 i 位置元素为结尾的「所有⼦数组」中和的最⼤和。
- 状态转移⽅程:
dp[i] 的所有可能可以分为以下两种:
- 子数组的长度为 1 :此时 dp[i] = nums[i] ;
- 子数组的长度⼤大于 1 :此时 dp[i] 应该等于 以 i - 1 做结尾的「所有⼦数组」中和 的最⼤值再加上 nums[i] ,也就是 dp[i - 1] + nums[i] 。
由于我们要的是「最大值」,因此应该是两种情况下的最⼤值,因此可得转移⽅程:
- dp[i] = max(nums[i], dp[i - 1] + nums[i]) 。
- 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使用这种技巧要注意两个点:
- 辅助结点里面的值要「保证后续填表是正确的」;
- 「下标的映射关系」。
在本题中,最前⾯加上⼀个格⼦,并且让 dp[0] = 0 即可。
- 填表顺序
根据「状态转移⽅程」易得,填表顺序为「从左往右」。
- 返回值:
状态表示为「以 i 为结尾的所有⼦数组」的最⼤值,但是最大子数组和的结尾我们是不确定的。
因此我们需要返回整个 dp 表中的最⼤值。
🚩代码实现
class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length + 1];int ret = Integer.MIN_VALUE;for (int i = 1; i < dp.length; i++) {dp[i] = Math.max(nums[i -1],dp[i - 1] + nums[i - 1]);ret = Math.max(ret,dp[i]);}return ret;}
}
🌴环形子数组的最大和
🚩题目描述
给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], …, nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
- 示例 1:
输入:nums = [1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3 - 示例 2:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10 - 示例 3:
输入:nums = [3,-2,2,-3]
输出:3
解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
class Solution {public int maxSubarraySumCircular(int[] nums) {}
}
🚩算法思路:
本题与「最大子数组和」的区别在于,考虑问题的时候不仅要分析「数组内的连续区域」,还要考虑「数组⾸尾相连」的⼀部分。结果的可能情况分为以下两种:
- 结果在数组的内部,包括整个数组;
- 结果在数组首尾相连的⼀部分上。
其中,对于第⼀种情况,我们仅需按照「最大子数组和」的求法就可以得到结果,记为 fmax 。
对于第⼆种情况,我们可以分析⼀下:
- 如果数组⾸尾相连的⼀部分是最⼤的数组和,那么数组中间就会空出来⼀部分;
- 因为数组的总和 sum 是不变的,那么中间连续的⼀部分的和⼀定是最小的;
因此,我们就可以得出⼀个结论,对于第⼆种情况的最⼤和,应该等于 sum - gmin ,其中gmin 表⽰数组内的「最⼩⼦数组和」。
两种情况下的最⼤值,就是我们要的结果。
但是,由于数组内有可能全部都是负数,第⼀种情况下的结果是数组内的最⼤值(是个负数),第⼆种情况下的 gmin == sum ,求的得结果就会是 0 。
若直接求两者的最⼤值,就会是 0 。但是实际的结果应该是数组内的最⼤值。对于这种情况,我们需要特殊判断⼀下。
由于「最⼤⼦数组和」的⽅法已经讲过,这⾥只提⼀下「最⼩⼦数组和」的求解过程,其实与「最⼤⼦数组和」的求法是⼀致的。⽤ f 表⽰最⼤和, g 表⽰最⼩和。
- 状态表示:
g[i] 表⽰:以 i 做结尾的「所有⼦数组」中和的最⼩值。
- 状态转移⽅程:
g[i] 的所有可能可以分为以下两种:
- ⼦数组的⻓度为 1 :此时 g[i] = nums[i] ;
- ⼦数组的⻓度⼤于 1 :此时 g[i] 应该等于 以 i - 1 做结尾的「所有⼦数组」中和的最⼩值再加上 nums[i] ,也就是 g[i - 1] + nums[i] 。
由于我们要的是最⼩⼦数组和,因此应该是两种情况下的最⼩值,因此可得转移⽅程:
- g[i] = min(nums[i], g[i - 1] + nums[i]) 。
- 初始化:
可以在最前⾯加上⼀个辅助结点,帮助我们初始化。使⽤这种技巧要注意两个点:
-
辅助结点⾥⾯的值要保证后续填表是正确的;
-
下标的映射关系。
在本题中,最前⾯加上⼀个格⼦,并且让 g[0] = 0 即可。
- 填表顺序:
根据状态转移⽅程易得,填表顺序为「从左往右」。
- 返回值:
- 先找到 f 表⾥⾯的最⼤值 -> fmax ;
- 找到 g 表⾥⾯的最⼩值 -> gmin ;
- 统计所有元素的和 -> sum ;
- 返回 sum == gmin ? fmax : max(fmax, sum - gmin)
🚩代码实现
public int maxSubarraySumCircular(int[] nums) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];int sum = 0;int fmax = Integer.MIN_VALUE;int gmin = Integer.MAX_VALUE;for(int i = 1; i <= n; i++) {int x = nums[i - 1];f[i] = Math.max(x, x + f[i - 1]);fmax = Math.max(fmax, f[i]);g[i] = Math.min(x, x + g[i - 1]);gmin = Math.min(gmin, g[i]);sum += x;}return sum == gmin ? fmax : Math.max(fmax, sum - gmin);}
🌲乘积最大子数组
🚩题目描述
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续
子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
- 示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。 - 示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
class Solution {public int maxProduct(int[] nums) {}
}
🚩算法思路:
这道题与「最大子数组和] 非常相似,我们可以效仿着定义⼀下状态表⽰以及状态转移:
- dp[i] 表示以 i 为结尾的所有子数组的最⼤乘积,
- dp[i] = max(nums[i], dp[i - 1] * nums[i]) ;
由于正负号的存在,我们很容易就可以得到,这样求 dp[i] 的值是不正确的。因为 dp[i - 1] 的信息并不能让我们得到 dp[i] 的正确值。
比如数组 [-2, 5, -2] ,用上述状态转移得到的 dp数组为 [-2, 5, -2] ,最⼤乘积为 5 。但是实际上的最⼤乘积应该是所有数相乘,结果为 20 。
究其原因,就是因为我们在求 dp[2] 的时候,因为 nums[2] 是⼀个负数,因此我们需要的是「 i - 1 位置结尾的最⼩的乘积 (-10) 」,这样⼀个负数乘以「最⼩值」,才会得到真实的最⼤值。
因此,我们不仅需要⼀个「乘积最⼤值的 dp 表」,还需要⼀个「乘积最⼩值的 dp 表」。
- 状态表⽰:
f[i] 表⽰:以 i 结尾的所有⼦数组的最⼤乘积,
g[i] 表⽰:以 i 结尾的所有⼦数组的最⼩乘积。
- 状态转移⽅程:
遍历每⼀个位置的时候,我们要同步更新两个 dp 数组的值。
对于 f[i] ,也就是「以 i 为结尾的所有⼦数组的最⼤乘积」,对于所有⼦数组,可以分为下⾯三种形式:
- ⼦数组的⻓度为 1 ,也就是 nums[i] ;
- ⼦数组的⻓度⼤于 1 ,但 nums[i] > 0 ,此时需要的是 i - 1 为结尾的所有⼦数组的最⼤乘积 f[i - 1] ,再乘上 nums[i] ,也就是 nums[i] * f[i - 1] ;
- ⼦数组的⻓度⼤于 1 ,但 nums[i] < 0 ,此时需要的是 i - 1 为结尾的所有⼦数组的最⼩乘积 g[i - 1] ,再乘上 nums[i] ,也就是 nums[i] * g[i - 1] ;(如果 nums[i] = 0 ,所有⼦数组的乘积均为 0 ,三种情况其实都包含了)
综上所述, f[i] = max(nums[i], max(nums[i] * f[i - 1], nums[i] * g[i -
1]) )。
对于 g[i] ,也就是「以 i 为结尾的所有⼦数组的最⼩乘积」,对于所有⼦数组,可以分为下⾯三种形式:
- 子数组的⻓度为 1 ,也就是 nums[i] ;
- 子数组的⻓度⼤于 1 ,但 nums[i] > 0 ,此时需要的是 i - 1 为结尾的所有子数组的最⼩乘积 g[i - 1] ,再乘上 nums[i] ,也就是 nums[i] * g[i - 1] ;
- 子数组的长度度⼤于 1 ,但 nums[i] < 0 ,此时需要的是 i - 1 为结尾的所有子数组的最⼤乘积 f[i - 1] ,再乘上 nums[i] ,也就是 nums[i] * f[i - 1] ;
综上所述, g[i] = min(nums[i], min(nums[i] * f[i - 1], nums[i] * g[i - 1])) 。
(如果 nums[i] = 0 ,所有⼦数组的乘积均为 0 ,三种情况其实都包含了)
- 初始化:
可以在最前面加上⼀个辅助结点,帮助我们初始化。使⽤这种技巧要注意两个点:
- 辅助结点里面的值要保证后续填表是正确的;
- 下标的映射关系。
在本题中,最前⾯加上⼀个格⼦,并且让 f[0] = g[0] = 1 即可。
- 填表顺序:
根据状态转移⽅程易得,填表顺序为「从左往右,两个表⼀起填」。
- 返回值:
返回 f 表中的最⼤值
🚩代码实现
class Solution {public int maxProduct(int[] nums) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];f[0] = 1;g[0] = 1;int ret = Integer.MIN_VALUE;for(int i = 1; i <= n; i++) {int x = nums[i - 1];int y = f[i - 1] * nums[i - 1];int z = g[i - 1] * nums[i - 1];f[i] = Math.max(x, Math.max(y, z));g[i] = Math.min(x, Math.min(y, z));ret = Math.max(ret, f[i]);}return ret;}
}
⭕总结
关于《【算法优选】 动态规划之子数组、子串系列——壹》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【算法优选】 动态规划之子数组、子串系列——壹
文章目录 🎋前言🎋最大子数组和🚩题目描述🚩算法思路🚩代码实现 🌴环形子数组的最大和🚩题目描述🚩算法思路:🚩代码实现 🌲乘积最大子数组&#x…...

PXE+Kickstart无人值守安装安装Centos7.9
文章目录 一、什么是PXE1、简介2、工作模式3、工作流程 二、什么是Kickstart1、简介2、触发方式 三、无人值守安装系统工作流程四、实验部署1、环境准备2、服务端:关闭防火墙和selinux3、添加一张仅主机的网卡4、配置仅主机的网卡4.1、修改网络连接名4.2、配IP地址4…...

C语言实现通讯录,包括增删改查以及动态开辟内存,写入文件等功能
文章目录 前言一、注意二、源码1. test.c源文件2. contact.h头文件3. contact.c源文件 总结 前言 C语言实现通讯录,包括增删改查以及动态开辟内存,写入文件等功能 一、注意 在通讯录菜单栏使用枚举定义PeoInfo类型时,每个结构体类型的成员…...
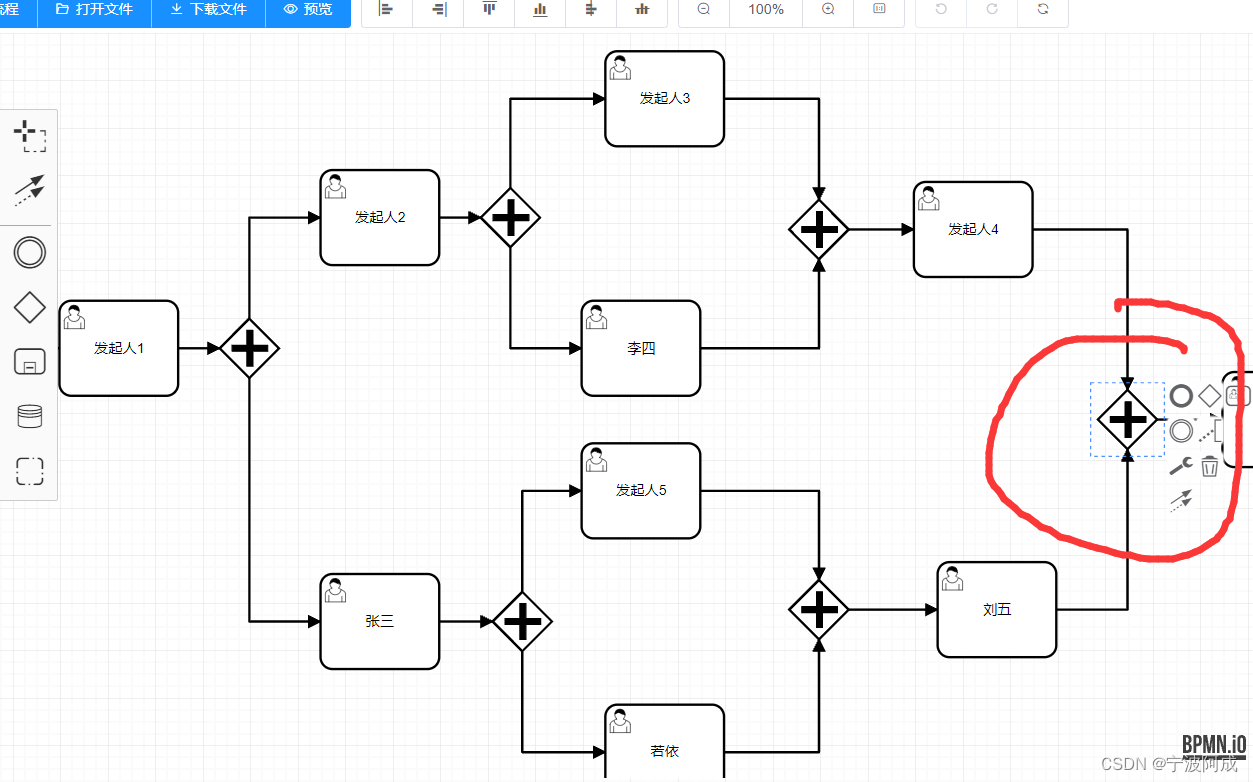
flowable多对并发网关跳转的分析
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 http://218.75.87.38:9666/ 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: h…...

【嵌入式——QT】QT集成Ymodem协议使用UDP进行传输
【嵌入式——QT】QT集成Ymodem协议使用UDP进行传输 Ymodem协议帧的数据格式帧头包号校验 通讯过程握手信号起始帧数据帧结束帧代码块 Ymodem命令 QT实现YmodemFileTransmit.hYmodemFileTransmit.cppBootLoader.hBootLoader.cppYmodem协议源码 Ymodem协议 帧的数据格式 帧头、…...
输入输出)
python笔记(17)输入输出
一、标准输入与输出简介 Python通过内置的sys模块管理标准输入(stdin)、标准输出(stdout)和标准错误(stderr)。但对大多数简单应用而言,直接使用内置函数就足够了。 二、输入:inpu…...

408数据结构总结复习笔记一:线性表
408数据结构总结复习笔记一:线性表 从现在开始慢慢更新我的考研复习笔记系列吧~ PS:主要是我自己个人复习过程中觉得重点的点,大家仅供参考哈~ 上岸!!!大家一起加油! 顺序表和链表的比较 顺序表链表存取…...

Docker——目录迁移
我们在生产环境中安装Docker时,默认的安装目录是/var/lib/docker,而通常情况下,规划给系统盘的目录一般为50G,该目录是比较小的,一旦容器过多或容器日志过多,就可能出现Docker无法运行的情况,所…...

SpringAMQP-消息转换器
这边发送消息接收消息默认是jdk的序列化方式,发送到服务器是以字节码的形式,我们看不懂也很占内存,所以我们要手动设置一下 我这边设置成json的序列化方式,注意发送方和接收方的序列化方式要保持一致 不然回报错。 引入依赖&#…...

轻松拿下指针(5)
文章目录 一、回调函数是什么二、qsort使用举例三、qsort函数的模拟实现 一、回调函数是什么 回调函数就是⼀个通过函数指针调⽤的函数。 如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被⽤来调⽤其所指向的函数 时&#x…...
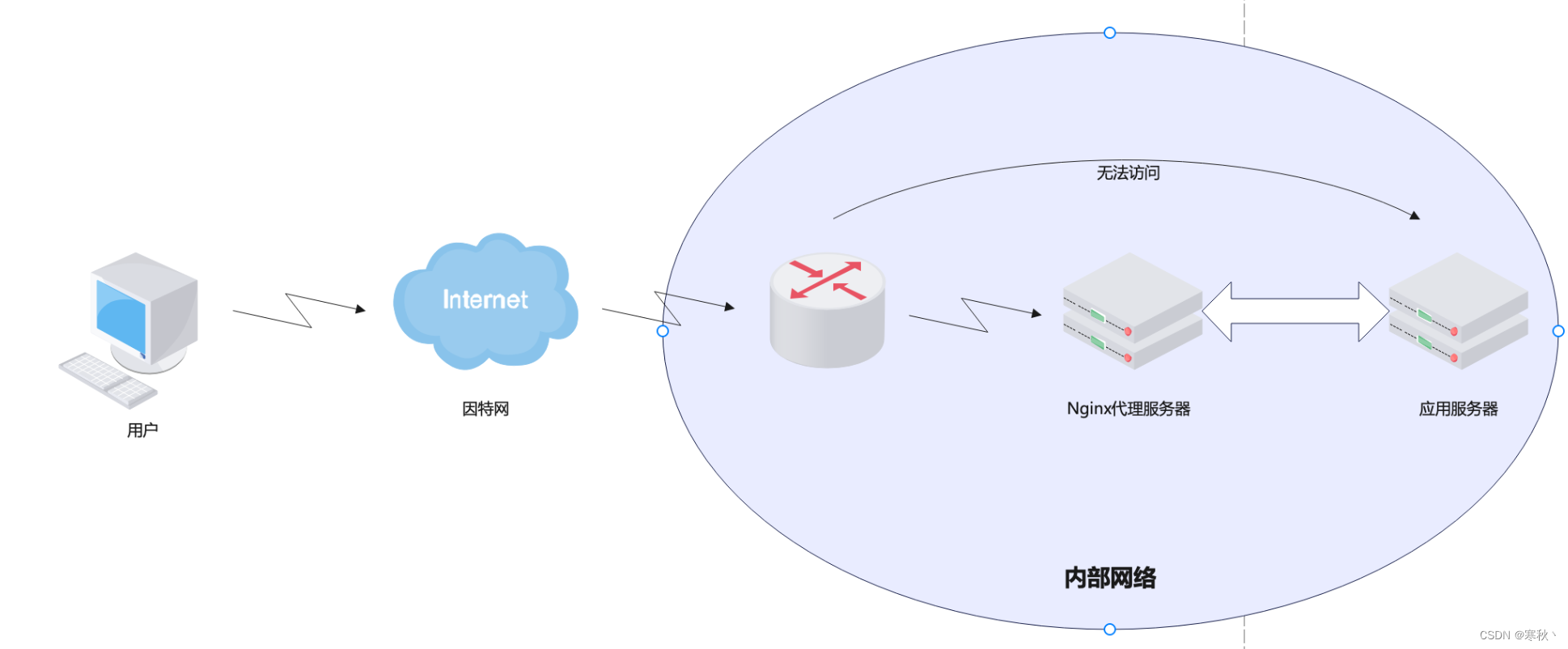
Nginx反向代理配置
一、介绍 Nginx 的反向代理功能在现代网络架构中扮演着至关重要的角色。首先,它充当了客户端与后端服务器之间的中介。当客户端发送请求时,这些请求先到达 Nginx 服务器,Nginx 会根据预先设定的规则和配置,将请求准确地转发到相应…...

突破编程界限:探索AI编程新境界
文章目录 一、AI编程助手1.1 Baidu Comate智能代码助手1.2 阿里云 通义灵码 二、场景需求三、体验步骤3.1 官网下载3.2 手动下载 四、试用感受4.1 提示4.2 注释生成代码4.3 代码生成4.4 选中生成注释4.5 查看变更&新建文件4.6 调优建议4.7 插件使用 五、结尾推荐 一、AI编程…...
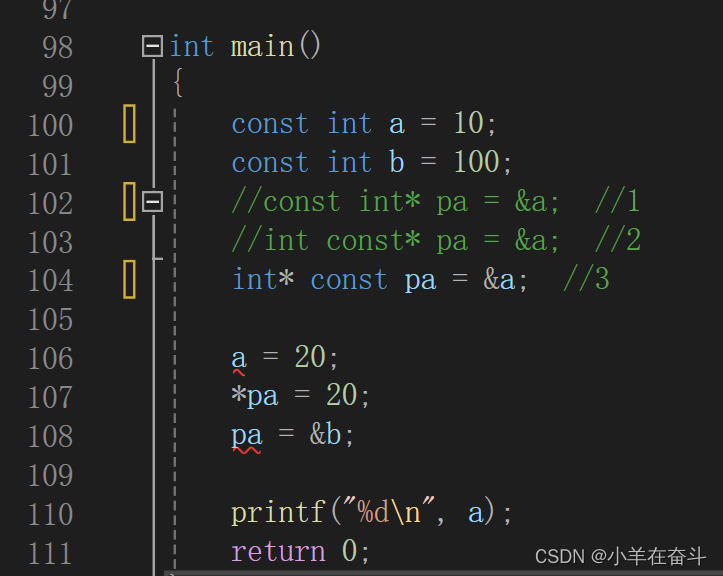
C语言(指针)2
Hi~!这里是奋斗的小羊,很荣幸各位能阅读我的文章,诚请评论指点,关注收藏,欢迎欢迎~~ 💥个人主页:小羊在奋斗 💥所属专栏:C语言 本系列文章为个人学习笔记&#x…...

go学习笔记
1基础搭建 1.1,安装vscode https://code.visualstudio.com/download 64位 1.2,Windows 下搭建Go 开发环境-安装和配置 SDK SDK 的全称(Software Development Kit 软件开发工具包) Go 语言的官网为:golang.org , 因为各种原因,可…...

MacApp自动化测试之Automator初体验
今天我们继续讲Automator的使用。 初体验 启动Automator程序,选择【工作流程】类型。从资源库区域依次将获取指定的URL、从网页中获得文本、新建文本文件三个操作拖进工作流创建区域。 然后修改内容,将获取指定的URL操作中的URL替换成https://www.cnb…...

Vue学习v-html
Vue学习v-html 一、前言1、基本用法2、注意事项 二、总结 一、前言 学习 Vue.js 中的 v-html 指令意味着你想要在你的应用程序中动态地渲染 HTML。这个指令允许你将数据中包含的 HTML 代码直接插入到你的模板中,而不是将其作为纯文本处理。虽然这个功能非常强大&am…...

C++并发:锁
一、前言 C中的锁和同步原语的多样化选择使得程序员可以根据具体的线程和数据保护需求来选择最合适的工具。这些工具的正确使用可以大大提高程序的稳定性和性能,本文讨论了部分锁。 二、std::lock 在C中,std::lock 是一个用于一次性锁定两个或多个互斥…...

Git | git log 和 git status 的区别
如是我闻: git log和git status是Git中的两个非常有用的命令,它们用于不同的目的,并提供不同类型的信息。 git log git log命令用于显示一个或多个分支的提交历史记录。这个命令会列出提交历史,包括每次提交的SHA-1哈希值、提交…...

Django 4.x 智能分页get_elided_page_range
Django智能分页 分页效果 第1页的效果 第10页的效果 带输入框的效果 主要函数 # 参数解释 # number: 当前页码,默认:1 # on_each_side:当前页码前后显示几页,默认:3 # on_ends:首尾固定显示几页&#…...
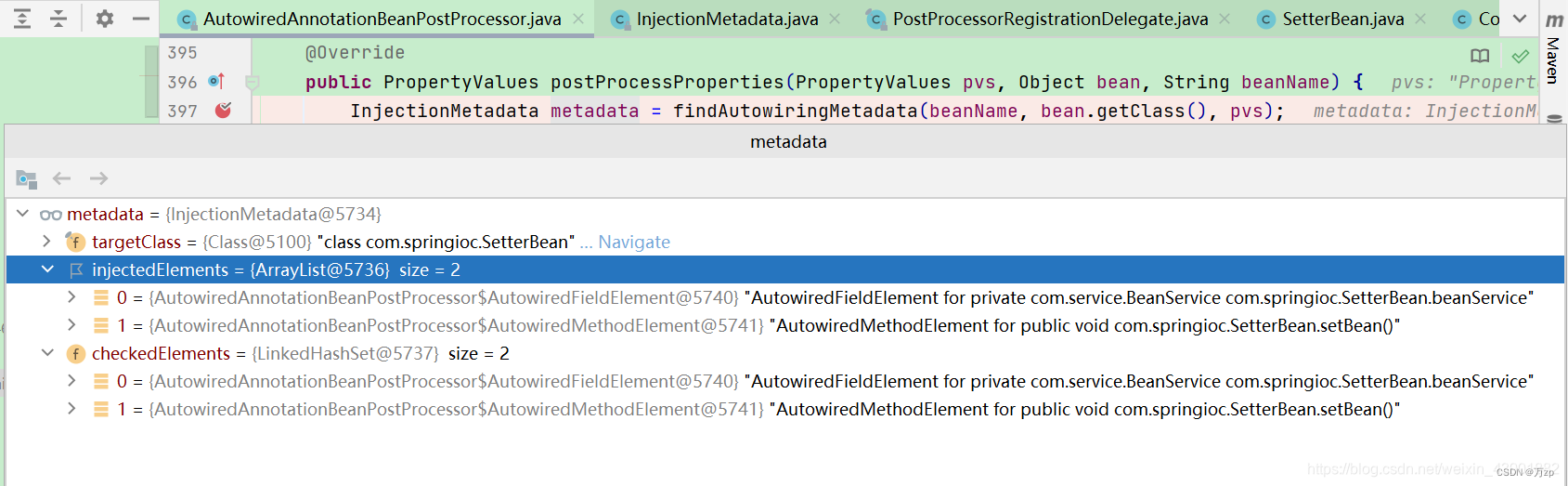
java-spring 09 下.populateBean (方法成员变量的注入@Autowird,@Resource)
1.在populateBean 方法中的一部分:用于Autowird,Resource注入 // 后处理器已经初始化boolean hasInstAwareBpps hasInstantiationAwareBeanPostProcessors();// 需要依赖检查boolean needsDepCheck (mbd.getDependencyCheck() ! AbstractBeanDefinitio…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
