探索数据结构:堆的具体实现与应用
✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:数据结构与算法
贝蒂的主页:Betty’s blog
1. 堆的概念
堆(Heap)是计算机科学中一类特殊的数据结构。堆通常是一个可以被看作一棵完全二树的数组对象,若满足:
- 任意节点的值>=其子节点的值。则称为大根堆。
- 任意节点的值<=其子节点的值。则称为小根堆。


2. 堆的实现方式
虽然堆是一种特殊的二叉树,它既可以用数组存储也可以用链式存储。但是考虑到其完全二叉树的特性,我们最好采用数组存储的方式,因为这样既方便访问,也并不会浪费格外的空间。

假设某个合法下标为i:
- 若双亲节点存在,下标为(i-1)/2。
- 若孩子节点存在,左孩子下标为2i+1,右孩子为2i+2。
3. 堆的功能
- 堆的初始化。
- 堆的插入。
- 堆的删除。
- 获取堆顶的元素。
- 堆的元素个数。
- 堆的判空。
- 输出堆。
- 建堆。
- 销毁堆。
4. 堆的声明
因为我用数组实现堆,所以堆的声明与顺序表类似。
typedef int HpDataType;
typedef struct Heap
{HpDataType* a;//存储数据int size;//大小int capacity;//容量
}Heap;
5. 堆的实现
5.1. 堆的初始化
5.1.1. 代码实现
void HeapInit(Heap* hp)//堆的初始化
{assert(hp);hp->a = NULL;hp->size = hp->capacity = 0;
}
5.1.2. 复杂度分析
- 时间复杂度:没有额外的时间消耗,时间复杂度为O(1)。
- 空间复杂度:没有额外的空间消耗,空间复杂度为O(1)。
5.2. 堆的插入
当我们堆进行插入时可能会破坏堆的原有结构,这时就需要我们对其进行向上调整。
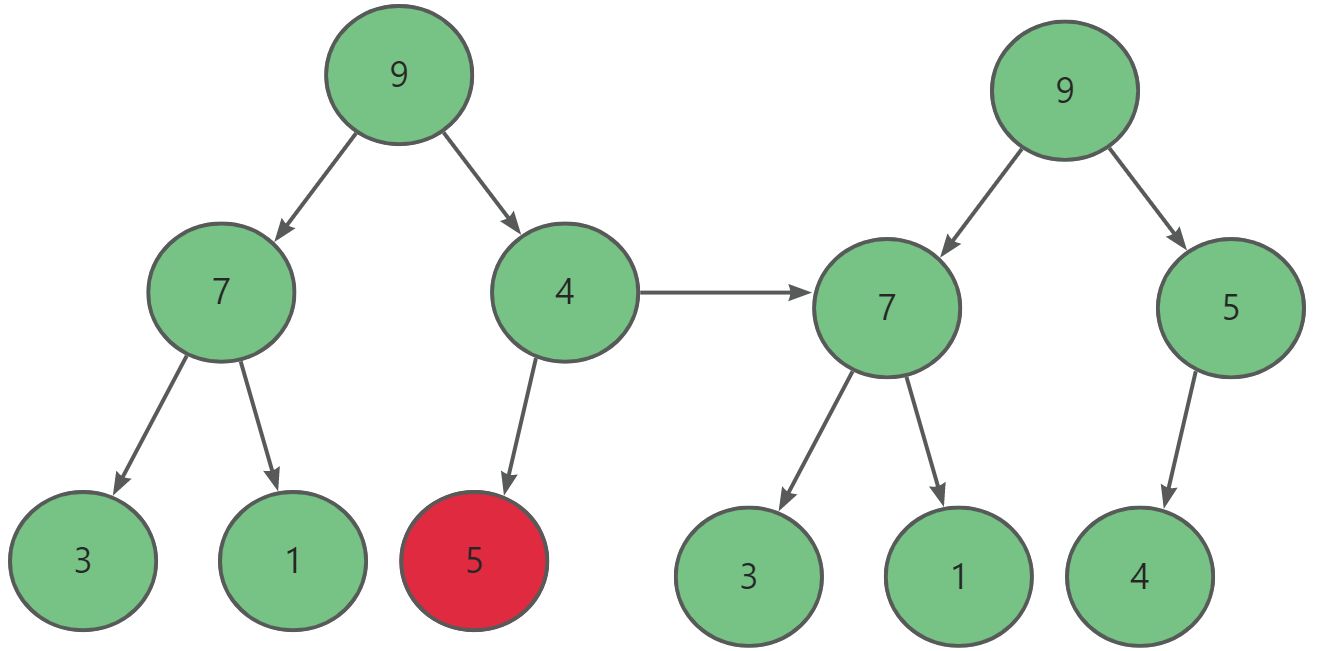
5.2.1. 代码实现
void AdjustUp(Heap* hp, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (hp->a[child] > hp->a[parent]){swap(&hp->a[child], &hp->a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPush(Heap* hp, HpDataType x)//堆的插入
{assert(hp);if (hp->size == hp->capacity){int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HpDataType* tmp = (HpDataType*)realloc(hp->a, newCapacity * sizeof(HpDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = newCapacity;}hp->a[hp->size] = x;hp->size++;AdjustUp(hp, hp->size - 1);//向上调整
}
5.2.2. 复杂度分析
- 时间复杂度:假设有N个节点,高度为h,2h -1=N。至少调整log2(N+1)-1次,所以时间复杂度为logN。
- 空间复杂度:没有开辟额外的空间,空间复杂度为O(1)。
5.3. 堆的删除
堆的删除是指删除堆顶的数据,如果我们删除堆顶元素并往前覆盖就可能打乱原有的亲缘关系。所以我们可以先将堆顶的元素与末尾元素交换,然后再进行向下调整·。

5.3.1. 代码实现
void swap(HpDataType* x1, HpDataType* x2)
{HpDataType tmp = *x1;*x1 = *x2;*x2 = tmp;
}
void
void AdjustDown(int* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;//默认左孩子更大while (child < n){ if (child + 1 < n && a[child + 1]> a[child]){++child;//右孩子}if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(Heap* hp)//删除堆顶元素
{assert(hp);assert(hp->size > 0);swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//删除最后一个数据AdjustDown(hp->a, hp->size, 0);//向下调整
}
5.3.2. 复杂度分析
- 时间复杂度:假设有N个节点,高度为h,2h -1=N。至少调整log2(N+1)-1次,所以时间复杂度为logN。
- 空间复杂度:没有开辟额外的空间,空间复杂度为O(1)。
5.4. 获取堆顶元素
5.4.1. 代码实现
HpDataType HeapTop(Heap* hp)//获取堆顶元素
{assert(hp);assert(hp->size > 0);return hp->a[0];
}
5.4.2. 复杂度分析
- 时间复杂度:没有额外的时间消耗,时间复杂度为O(1)。
- 空间复杂度:没有额外的空间消耗,空间复杂度为O(1)。
5.5. 获取堆的元素个数
5.5.1. 代码实现
size_t HeapSize(Heap* hp)//堆的大小
{assert(hp);return hp->size;
}
5.5.2. 复杂度分析
- 时间复杂度:没有额外的时间消耗,时间复杂度为O(1)。
- 空间复杂度:没有额外的空间消耗,空间复杂度为O(1)。
5.6. 判断堆是否为空
5.6.1. 代码实现
bool HeapEmpty(Heap* hp)//判断堆是否为空
{assert(hp);return hp->size == 0;
}
5.6.2. 复杂度分析
- 时间复杂度:没有额外的时间消耗,时间复杂度为O(1)。
- 空间复杂度:没有额外的空间消耗,空间复杂度为O(1)。
5.7. 输出堆
5.7.1. 代码实现
void HeapDisplay(Heap* hp)//堆的打印
{for (int i = 0; i < hp->size; ++i){printf("%d ", hp->a[i]);}printf("\n");
}
5.7.2. 复杂度分析
- 时间复杂度:遍历整个数组,时间复杂度为O(N)。
- 空间复杂度:没有额外的空间消耗,空间复杂度为O(1)。
5.8. 建堆
5.8.1. 代码实现
void HeapCreatUp(Heap* hp,HpDataType* arr,int n)//向上调整建堆
{assert(hp && arr);for (int i = 0; i < n; i++){HeapPush(hp, arr[i]);}
}
void HeapCreatDown(Heap* hp, HpDataType* arr, int n)//向下调整建堆
{assert(hp && arr);HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}hp->a = tmp;memcpy(hp->a, arr, sizeof(HpDataType) * n);hp->size = n;hp->capacity = n;for (int i = ((n - 1) - 1) / 2; i >= 0; i--)//从最后一个元素开始{AdjustDown(hp->a, n, i);}
}
5.8.2. 复杂度分析
假设高度为h,节点个数为N。如果是向上调整建堆:

F ( N ) = 2 1 × 1 + 2 2 × 2 + . . . + 2 h − 1 × ( h − 1 ) 2 F ( N ) = 2 2 × 1 + 2 3 × 2 + . . . + 2 h − 1 × ( h − 1 ) + 2 h × ( h − 1 ) 2 F ( N ) − F ( N ) = − 2 1 − 2 2 − 2 3 − . . . 2 h − 1 + 2 h × ( h − 1 ) = − 2 h + 2 − 2 h + 2 h × h F ( N ) = 2 h × ( h − 2 ) + 2 , N = 2 h − 1 F ( N ) = ( N + 1 ) × ( l o g 2 ( N + 1 ) − 2 ) + 2 F(N)=2^1×1+2^2×2+...+2^{h-1}×(h-1)\\ 2F(N)=2^2×1+2^3×2+...+2^{h-1}×(h-1)+2^h×(h-1)\\ 2F(N)-F(N)=-2^1-2^2-2^3-...2^{h-1}+2^h×(h-1)=-2^h+2-2^h+2^h×h\\ F(N)=2^h×(h-2)+2,N=2^h-1\\ F(N)=(N+1)×(log2(N+1)-2)+2 F(N)=21×1+22×2+...+2h−1×(h−1)2F(N)=22×1+23×2+...+2h−1×(h−1)+2h×(h−1)2F(N)−F(N)=−21−22−23−...2h−1+2h×(h−1)=−2h+2−2h+2h×hF(N)=2h×(h−2)+2,N=2h−1F(N)=(N+1)×(log2(N+1)−2)+2
如果是向下调整建堆:
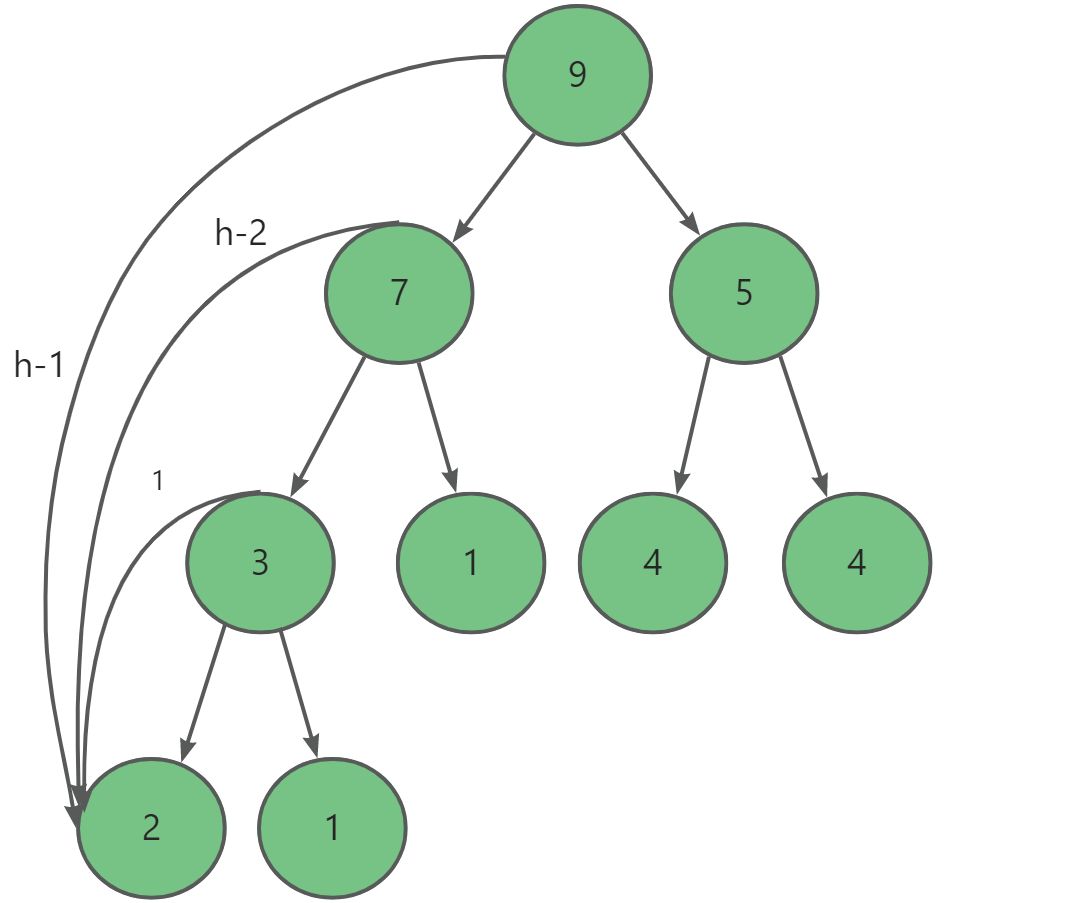
F ( N ) = 2 h − 2 × 1 + 2 h − 3 × 2 + . . . + 2 0 × ( h − 1 ) 2 F ( N ) = 2 h − 1 × 1 + 2 h − 2 × 2 + . . . + 2 1 × ( h − 1 ) 2 F ( N ) − F ( N ) = 2 h − 1 + 2 h − 2 + . . . 2 1 − 2 0 × ( h − 1 ) = 2 h − 1 − h F ( N ) = 2 h − 1 − h , N = 2 h − 1 F ( N ) = N − l o g 2 ( N + 1 ) F(N)=2^{h-2}×1+2^{h-3}×2+...+2^0×(h-1)\\ 2F(N)=2^{h-1}×1+2^{h-2}×2+...+2^1×(h-1)\\ 2F(N)-F(N)=2^{h-1}+2^{h-2}+...2^1-2^0×(h-1)=2^h-1-h\\ F(N)=2^h-1-h,N=2^h-1\\ F(N)=N-log2(N+1) F(N)=2h−2×1+2h−3×2+...+20×(h−1)2F(N)=2h−1×1+2h−2×2+...+21×(h−1)2F(N)−F(N)=2h−1+2h−2+...21−20×(h−1)=2h−1−hF(N)=2h−1−h,N=2h−1F(N)=N−log2(N+1)
- 时间复杂度:向上调整建堆最后一排调整h-1次,倒数第二排调整h-2次…时间复杂度为NlogN。向下调整建堆倒数第二排调整1次,倒数第二排调整2…第一排调整h-1次。时间复杂为O(N)。
- 空间复杂度:无论是向上调整建堆还是向下调整建堆都需开辟N个空间,所以空间复杂度为O(N)。
5.9. 销毁堆
5.9.1. 代码实现
void HeapDestroy(Heap* hp)//销毁堆
{assert(hp);free(hp->a);hp->size = hp->capacity = 0;
}
5.9.2. 复杂度分析
- 时间复杂度:没有额外的时间消耗,时间复杂度为O(1)。
- 空间复杂度:没有额外的空间消耗,空间复杂度为O(1)。
5.10. 完整代码
5.10.1. Heap.h
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<assert.h>
typedef int HpDataType;
typedef struct Heap
{HpDataType* a;//存储数据int size;//大小int capacity;//容量
}Heap;
void HeapInit(Heap* hp);//堆的初始化
void AdjustUp(Heap* hp, int child);//向上调整
void HeapPush(Heap* hp, HpDataType x);//堆的插入
bool HeapEmpty(Heap* hp);//判断堆是否为空
size_t HeapSize(Heap* hp);//堆的大小
void AdjustDown(int* a, int n, int parent);//向下调整
void HeapPop(Heap* hp);//删除堆顶元素
HpDataType HeapTop(Heap* hp);//获取堆顶元素
void HeapDisplay(Heap* hp);//堆的打印
void HeapDestroy(Heap* hp);//销毁堆
void HeapCreatUp(Heap* hp,HpDataType* arr, int n);//向上调整建堆
void HeapCreatDown(Heap* hp,HpDataType* arr, int n);//向下调整建堆
5.10.2. Heap.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void HeapInit(Heap* hp)//堆的初始化
{assert(hp);hp->a = NULL;hp->size = hp->capacity = 0;
}
void swap(HpDataType* x1, HpDataType* x2)
{HpDataType tmp = *x1;*x1 = *x2;*x2 = tmp;
}
void AdjustUp(Heap* hp, int child)//向上调整
{int parent = (child - 1) / 2;while (child > 0){if (hp->a[child] > hp->a[parent]){swap(&hp->a[child], &hp->a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPush(Heap* hp, HpDataType x)//堆的插入
{assert(hp);if (hp->size == hp->capacity){int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HpDataType* tmp = (HpDataType*)realloc(hp->a, newCapacity * sizeof(HpDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}hp->a = tmp;hp->capacity = newCapacity;}hp->a[hp->size] = x;hp->size++;AdjustUp(hp, hp->size - 1);//向上调整
}
void AdjustDown(int* a, int n, int parent)//向下调整
{int child = parent * 2 + 1;//默认左孩子更大while (child < n){ if (child + 1 < n && a[child + 1]> a[child]){++child;//右孩子}if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapPop(Heap* hp)//删除堆顶元素
{assert(hp);assert(hp->size > 0);swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//删除最后一个数据AdjustDown(hp->a, hp->size, 0);//向下调整
}HpDataType HeapTop(Heap* hp)//获取堆顶元素
{assert(hp);assert(hp->size > 0);return hp->a[0];
}bool HeapEmpty(Heap* hp)//判断堆是否为空
{assert(hp);return hp->size == 0;
}size_t HeapSize(Heap* hp)//堆的大小
{assert(hp);return hp->size;
}void HeapDisplay(Heap* hp)//堆的打印
{for (int i = 0; i < hp->size; ++i){printf("%d ", hp->a[i]);}printf("\n");
}
void HeapCreatUp(Heap* hp,HpDataType* arr,int n)//向上调整建堆
{assert(hp && arr);for (int i = 0; i < n; i++){HeapPush(hp, arr[i]);}
}
void HeapCreatDown(Heap* hp, HpDataType* arr, int n)//向下调整建堆
{assert(hp && arr);HpDataType* tmp = (HpDataType*)malloc(sizeof(HpDataType) * n);if (tmp == NULL){perror("malloc fail");exit(-1);}hp->a = tmp;memcpy(hp->a, arr, sizeof(HpDataType) * n);hp->size = n;hp->capacity = n;for (int i = ((n - 1) - 1) / 2; i >= 0; i--)//从最后一个元素开始{AdjustDown(hp->a, n, i);}
}
void HeapDestroy(Heap* hp)//销毁堆
{assert(hp);free(hp->a);hp->size = hp->capacity = 0;
}
6. Top-K问题
6.1. 问题分析
Top-K问题简单来说就是求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。这个问题在我们日常生活中非常常见,比如说:游戏中活跃度前十的玩家,世界五百强企业等等。
解决这个问题常见的思路就是遍历或者排序,但是当数据量较大时这种方法就并不适用了。这时我们就需要建堆来处理,具体操作方法如下:
- 用数据集合中前K个元素来建堆。
- 前k个最大的元素,则建小堆。
- 前k个最小的元素,则建大堆。
- 用剩余的N - K个元素依次与堆顶元素来比较,不满足条件则替换堆顶元素。
void TopK(int* a, int n, int k)
{//建堆int* kminHeap = (int*)malloc(sizeof(int) * k);if (kminHeap == NULL){perror("malloc fail");exit(-1);}//将前k个数据放入堆中for (int i = 0; i < k; i++){kminHeap[i] = a[i];}//向下调整法建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminHeap, k, i);}//依次比较for (int i = k; i < n; i++){if (a[i] > kminHeap[0]){kminHeap[0] = a[i];AdjustDown(kminHeap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", kminHeap[i]);}printf("\n");free(kminHeap);
}
void TestTopk()
{int n = 10000;int* a = (int*)malloc(sizeof(int) * n);srand(time(0));for (size_t i = 0; i < n; ++i){a[i] = rand() % 1000000;}a[5] = 1000000 + 1;a[1231] = 1000000 + 2;a[531] = 1000000 + 3;a[5121] = 1000000 + 4;a[115] = 1000000 + 5;a[2335] = 1000000 + 6;a[9999] = 1000000 + 7;a[76] = 1000000 + 8;a[423] = 1000000 + 9;a[3144] = 1000000 + 10;TopK(a, n, 10);
}

6.2. 复杂度分析
- 时间复杂度:建堆时间为K,向下调整的最坏时间为(N-K)*logK。所以时间复杂度为NlogK。
- 空间复杂度:建堆会开辟K的个空间,所以空间复杂度为logK。
相关文章:

探索数据结构:堆的具体实现与应用
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. 堆的概念 堆(Heap)是计算机科学中一类特殊的数据结构。堆通常是一个…...
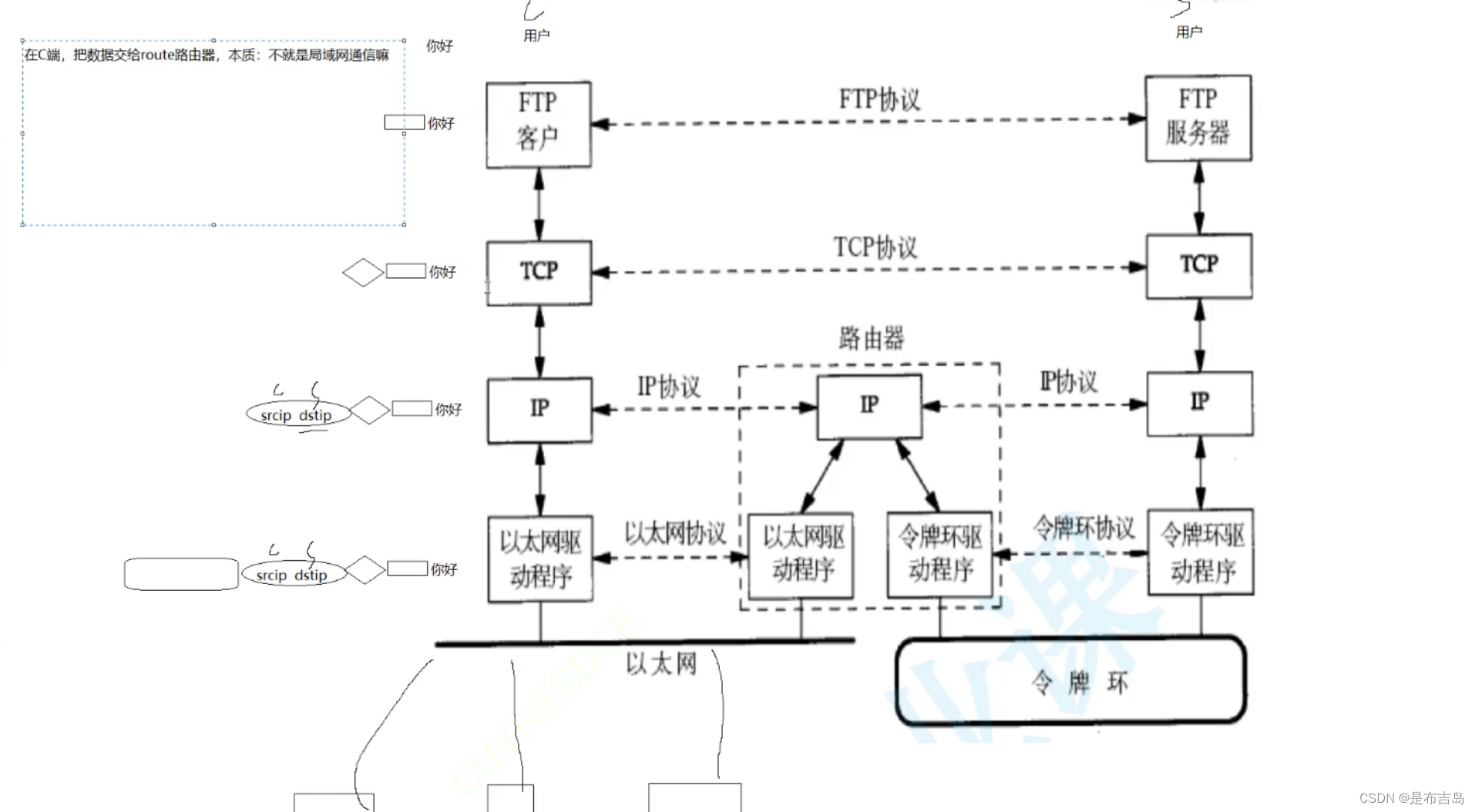
网络2--MAC地址,IP地址的理解
引入: 每一张主机都会有一张网卡,每一张网卡都有一个48bit位的序列号 当我们的热点被连上,你查看时,就会出现MAC地址,IP地址 那么他们两个是什么呢??? MAC地址 在同一个局域网中…...

类型的转换
首先我们要了解java中的数据类型转换是指将一种数据类型转换成另一种数据类型的过程。 什么时候会用到?我觉得两种情况会用到 等号左右两边类型不一致(一般发生在赋值时)不同类型的数据参与运算(一般发生在计算时) 转…...

memset函数
让我们先看两个代码 memset(dp, 0x3f, sizeof(dp)); for (int i 0; i < 5; i)cout << dp[i] << " "; memset(dp, 127, sizeof(dp)); for (int i 0; i < 5; i)cout << dp[i] << " "; 代码结果如下: 现在我们来分…...

Java面向对象——多态
即同一个方法可以根据发送对象的不同而采用多种不同的行为方式。 一个对象的实际类型是确定的,但可以指向对象的引用的类型有很多(父类,有关系的类)。 多态存在的条件: 1. 有继承关系; 2. 子类重写父类…...
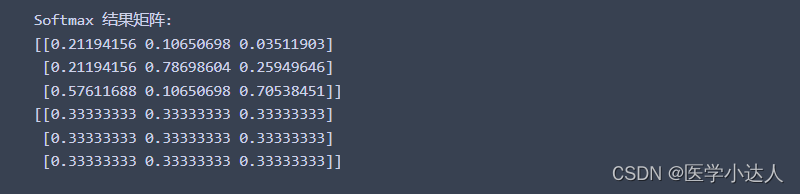
python 对矩阵与矩阵之间对应位置的元素,做softmax操作,代码实战
1.对矩阵中对应位置的元素,做softmax 对于一个向量,softmax函数会对其中每一个元素进行指数运算,然后除以所有元素指数和的结果。当将其应用到多个矩阵的相应位置上时,我们实际上是在对每个位置的一组数(从各个矩阵的同…...

Angular前端项目在Apache httpd服务器上的部署
Apache Httpd和Tomcat主要区别:Tomcat是一个Java Servlet容器,用于运行Java Servlet和JavaServer Pages(JSP),而Apache HTTP服务器是一个通用的Web服务器,用于提供静态和动态内容。 Apache httpd安装&#…...

Oracle 更改数据文件位置的几种常用方式
Oracle 更改数据文件位置的几种常用方式 A.归档模式下 1、offline 表空间:alter tablespace tablespace_name offline; 2、复制数据文件到新的目录; 3、rename 修改表空间,并修改控制文件; 4、online 表空间…...

【opencv】图像畸变校正
接上篇文章:【鱼眼+普通相机】相机标定 附代码: 方法一: 使用cv2.undistort """Create May 11, 2024author Wang Jiajun """import cv2 import numpy as npdef correct(img,camera_fileE:/cali…...

Charger之二输入电压动态电源原理(VIN-DPM)
主要内容 Charger的VIN-DPM 前篇内容:电池管理IC(Charger)了解一下? 领资料:点下方↓名片关注回复:粉丝群 正文 一、 VIN-DPM概念 VIN-DPM是指输入电压动态电源管理(Input voltage dynamic…...
【半夜学习MySQL】表结构的操作(含表的创建、修改、删除操作,及如何查看表结构)
🏠关于专栏:半夜学习MySQL专栏用于记录MySQL数据相关内容。 🎯每天努力一点点,技术变化看得见 文章目录 创建表查看表结构修改表删除表 创建表 语法: create table table_name(field1 datatype,field2 datatype,fiel…...
曲线救国:window 安装 docker
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益: 了解大厂经验拥有和大厂相匹配的技术等 希望看什么,评论或者私信告诉我! 文章目录 一…...

番外篇 | 利用PyQt5+YOLOv5来搭建目标检测系统(附可视化界面+功能介绍+源代码)
前言:Hello大家好,我是小哥谈。PyQt5是一个Python绑定的Qt库,是用于创建图形用户界面(GUI)和其他应用程序组件的工具包。PyQt5提供了许多GUI元素,如按钮、文本框、标签等,也提供了许多Qt的功能,如网络、数据库、XML等。通过PyQt5可以在Python中使用Qt的丰富功能和强大的工…...
Pascal Content数据集
如果您想使用Pascal Context数据集,请安装Detail,然后运行以下命令将注释转换为正确的格式。 1.安装Detail 进入项目终端 #即 这是在我自己的项目下直接进行克隆操作: git clone https://github.com/zhanghang1989/detail-api.git $PASCAL…...
【Unity】使用Resources.LoadAll读取文件的顺序问题
最近在做客户的一个项目,其中的一个模块使用到了照片,但是发现了一个很严重的问题。当你在使用Unity的时候,它竟然不按照顺序读取?这个机器人是不是逻辑有问题?如下图: 名字脱敏了哈。。。 照片比较多&…...
pdf怎么标注红色方框?五种PDF标注红色方框方法
pdf怎么标注红色方框?在当今数字化时代,PDF文档已成为我们日常工作和学习中不可或缺的一部分。然而,如何在海量的PDF文件中快速、准确地标注出重要信息,让内容更加醒目呢?今天,我将向大家介绍五种PDF标注红…...

C++字符串细节,面试题06
文章目录 22. 字符串22.1. 字符数组 vs 字符指针 vs 常量字符指针 vs string22.2. strcpy vs sprintf vs memcpy22.3. strlen vs length vs size vs sizeof22.4. 字符串之间的转换22.5 其他数据类型与字符串之间的转换22.6 字符串分割 22. 字符串 22.1. 字符数组 vs 字符指针 …...
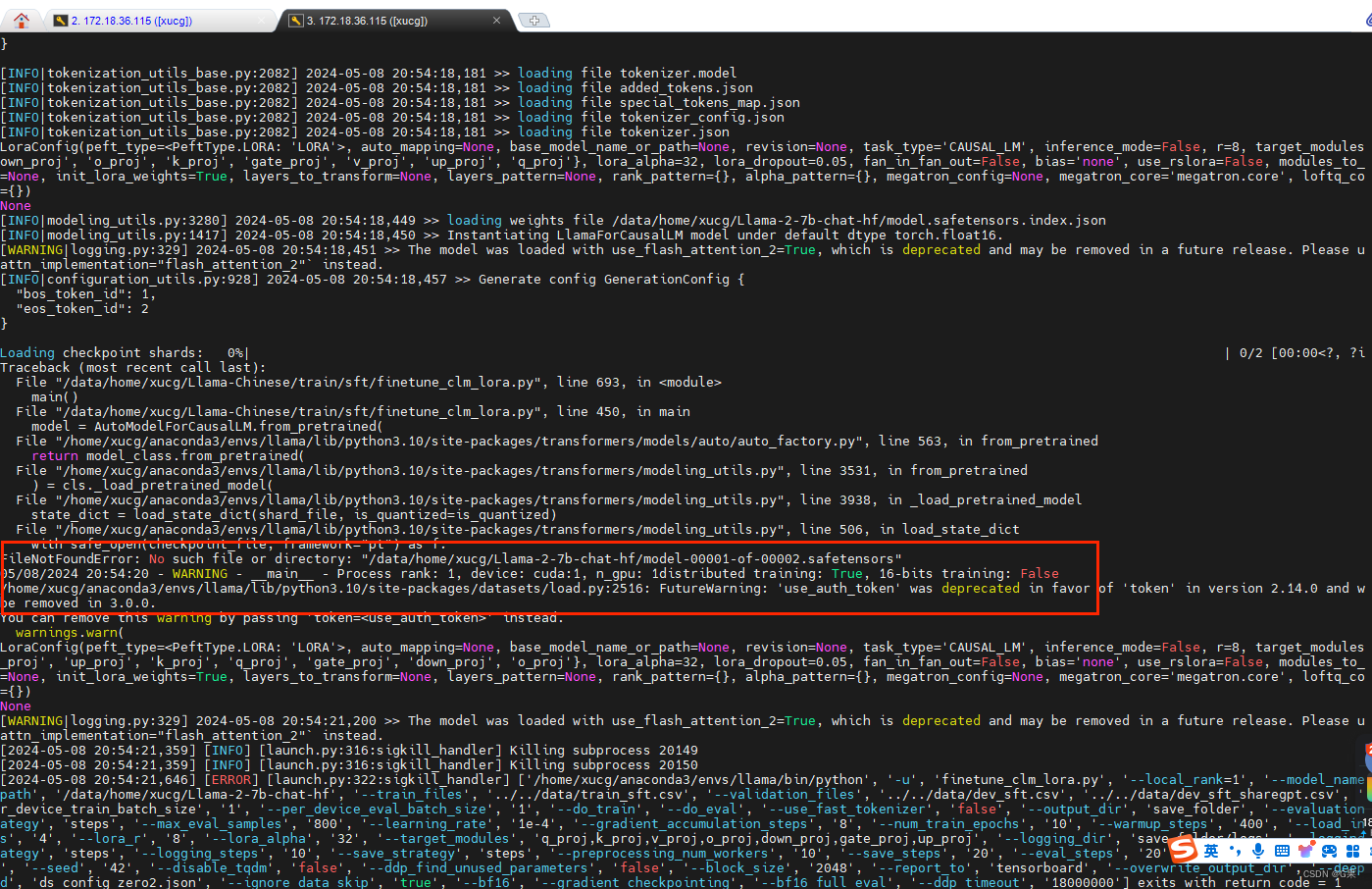
AutoModelForCausalLM.from_pretrained 函数调用本地权重报错
文章目录 1、代码报错的位置(前情提要)finetune_lora.shfintune_clm_lora.py 2、报错截图2.1、huggingfaces上的 meta-llama/Llama-2-7b-chat-hf2.2、服务器上模型文件路径 3、特别注意事项 1、代码报错的位置(前情提要) 在终端直…...

【qt】动态属性
这里写目录标题 一.属性1.属性的好处2.添加属性3.使用属性 二.只读属性 一.属性 1.属性的好处 说到属性(property),你们会想到什么?我会联想到特点,就是一类对象所特有的,在C中,成员数据就是这…...
Git知识点总结
目录 1、版本控制 1.1什么是版本控制 1.2常见的版本控制工具 1.3版本控制分类 2、集中版本控制 SVN 3、分布式版本控制 Git 2、Git与SVN的主要区别 3、软件下载 安装:无脑下一步即可!安装完毕就可以使用了! 4、启动Git 4.1常用的Li…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

