深入学习 torch.distributions
0. 引言
前几天分几篇博文精细地讲述了《von Mises-Fisher 分布》, 以及相应的 PyTorch 实现《von Mises-Fisher Distribution (代码解析)》, 其中以 Uniform 分布为例简要介绍了 torch.distributions 包的用法. 本以为已经可以了, 但这两天看到论文 The Power Spherical distribution 的代码, 又被其实现分布的方式所吸引.
Power Spherical 分布与 von Mises Fisher 分布类似, 只不过将后者概率密度函数中的指数函数换成了多项式函数: f p ( x ; μ , κ ) ∝ e x p ( κ μ ⊺ x ) ⇓ f p ( x ; μ , κ ) ∝ ( 1 + μ ⊺ x ) κ \begin{aligned} f_p(\bm{x}; \bm{\mu}, \kappa) &\propto exp(\kappa \bm{\mu}^\intercal \bm{x}) \\ &\Downarrow\\ f_p(\bm{x}; \bm{\mu}, \kappa) &\propto (1+\bm{\mu}^\intercal \bm{x})^\kappa \\ \end{aligned} fp(x;μ,κ)fp(x;μ,κ)∝exp(κμ⊺x)⇓∝(1+μ⊺x)κ 采样框架基本一致, 且这么做可以使边缘 t t t 的线性变换 t + 1 2 ∼ B e t a ( p − 1 2 + κ , p − 1 2 ) \frac{t+1}{2} \sim Beta(\frac{p-1}{2}+\kappa, \frac{p-1}{2}) 2t+1∼Beta(2p−1+κ,2p−1), 从而避免了接受-拒绝采样过程.
当然, 按照之前的 VonMisesFisher 的写法, 这个 t 的采样大概是这样:
z = beta.sample(sample_shape)
t = 2 * z - 1
但现在我遇到了这种写法:
class MarginalTDistribution(tds.TransformedDistribution):arg_constraints = {'dim': constraints.positive_integer,'scale': constraints.positive,}has_rsample = Truedef __init__(self, dim, scale, validate_args=None):self.dim = dimself.scale = scalesuper().__init__(tds.Beta( # 用 Beta 分布转换, z 服从 Beta(α+κ,β)(dim - 1) / 2 + scale, (dim - 1) / 2, validate_args=validate_args),transforms=tds.AffineTransform(loc=-1, scale=2), # t=2z-1 是想要的边缘分布随机数)
然后就可以进行对 t t t 的采样了.

我们可以看到其基本架构, 本文将详细解析其内部的具体细节.
相关文章:

深入学习 torch.distributions
0. 引言 前几天分几篇博文精细地讲述了《von Mises-Fisher 分布》, 以及相应的 PyTorch 实现《von Mises-Fisher Distribution (代码解析)》, 其中以 Uniform 分布为例简要介绍了 torch.distributions 包的用法. 本以为已经可以了, 但这两天看到论文 The Power Spherical dist…...
Java中的判断校验非空问题
目录 字符串 字符串是空的情况 字符串不是空的情况 对象 对象是空的情况 对象不是空的情况 前端传的 int ,double类型等等 Optional 判断情况 https://www.cnblogs.com/zhangboyu/p/7580262.htmlhttps://www.cnblogs.com/zhangboyu/p/7580262.html 值为空的情况,不会…...

webman使用summernote富文本编辑器
前言 Summernote富文本编辑器功能强大,可以直接从word直接复制内容过来而不破坏原有的文档格式,非常适合做商品详情等内容的编辑工具。本文将展示如何在php高性能框架webman中使用summernote编辑器。 下载 去Bootstrap 中文网、Summernote、jQuery官网…...
)
jQuery里添加事件 (代码)
直接上代码 <!DOCTYPE html> <html><head></head><body><input type"text" placeholder"城市" id"city" /><input type"button" value"添加" id"btnAdd" /><ul id…...
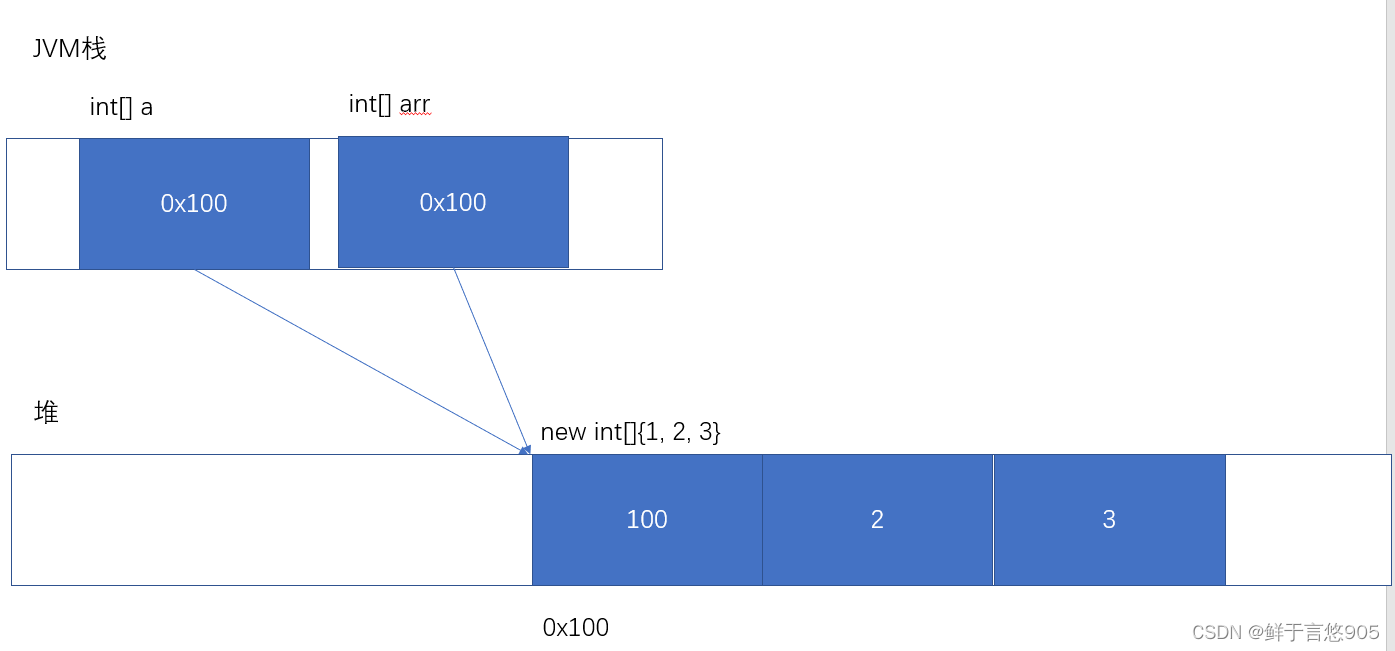
Java数组的使用
Java数组的使用 前言一、数组基本用法什么是数组注意事项创建数组基本语法代码示例注意事项 数组的使用代码示例获取长度 & 访问元素注意事项 下标越界遍历数组使用 for-each 遍历数组 二、数组作为方法的参数基本用法代码示例打印数组内容 理解引用类型代码示例参数传内置…...
如何参与github开源项目并提交PR
👽System.out.println(“👋🏼嗨,大家好,我是代码不会敲的小符,目前工作于上海某电商服务公司…”); 📚System.out.println(“🎈如果文章中有错误的地方,恳请大家指正&…...

拼多多携手中国农业大学,投建陕西佛坪山茱萸科技小院
5月16日下午,中国农业大学陕西佛坪山茱萸科技小院在佛坪县银厂沟村揭牌。佛坪县素有“中国山茱萸之乡”的美誉,是全国山茱萸三大基地之一,当地山茱萸是国家地理标志产品,山茱萸肉产量位居全国第二。 为充分发挥佛坪县得天独厚的山…...

技术前沿 |【自回归视觉模型ImageGPT】
自回归视觉模型ImageGPT 引言一、ImageGPT的基本原理与创新之处二、ImageGPT在图像生成、理解等视觉任务上的应用三、ImageGPT对后续视觉Transformer模型发展的影响四、ImageGPT的深入应用 引言 在人工智能的飞速发展中,视觉模型作为其中一个重要的分支,…...
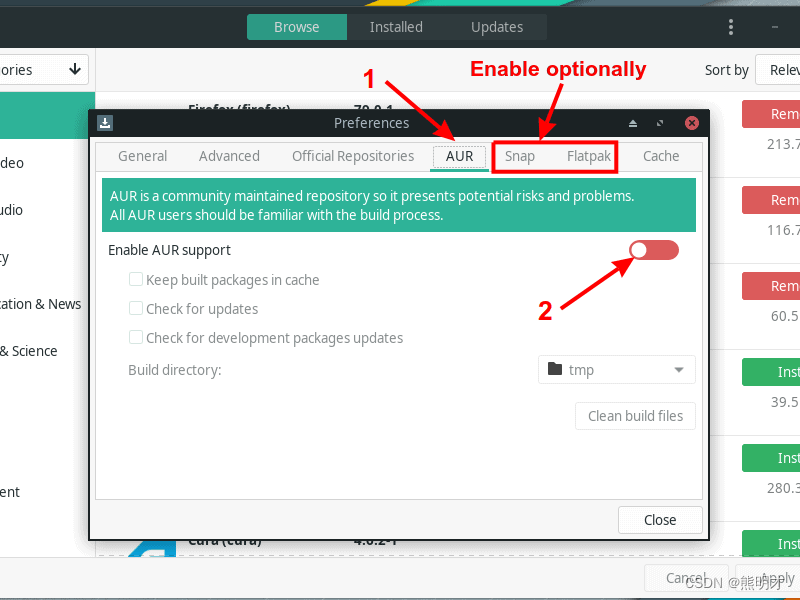
Manjaro linux install RedisGUI (RedisInsight)亲测2024-5-25
Arch 用户仓库(Arch User Repository)(AUR) 是用户选择 基于 Arch Linux 的系统 的一个主要理由。你可以在 AUR 中访问到大量的附加软件。 (LCTT 译注:AUR 中的 PKGBUILD 均为用户上传且未经审核,使用者需要自负责任,在构建软件包前请注意检…...

debian/control文件中常见字段的介绍
1 简介 在Debian或基于Debian的发行版中,debian/control文件是软件包管理的关键部分。它包含了软件包的各种元数据和安装脚本信息,用于软件包管理系统(如dpkg)识别如何处理该软件包。以下是debian/control文件中常见字段的详细介…...

c++题目_农场和奶牛
𝐵B 头奶牛 (1≤𝐵≤25000)(1≤B≤25000),有 𝑁(2𝐵≤𝑁≤50000)N(2B≤N≤50000) 个农场,编号 11 到 𝑁N,有 𝑀(𝑁−1≤𝑀≤100000)M(…...
DDD领域设计在“图生代码”中的应用实践
前言 领域驱动设计(简称 ddd)概念来源于2004年著名建模专家Eric Evans 发表的他最具影响力的书籍:《领域驱动设计——软件核心复杂性应对之道》(Domain-Driven Design –Tackling Complexity in the Heart of Software),简称Evans DDD。领域…...

LabVIEW舱段测控系统开发
LabVIEW舱段测控系统开发 在航空技术飞速发展的当下,对于航空器的测控系统的需求日益增加,特别是对舱段测控系统的设计与实现。开发了一款基于LabVIEW开发的舱段测控系统,包括系统设计需求、系统组成、工作原理以及系统实现等方面。 开发了…...

[leetcode]第 n个丑数
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。 示例: 输入: n 10 输出: 12 解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。 1 2 3 说明: 1 是丑数。 n 不超过1690。 class Solution {public…...
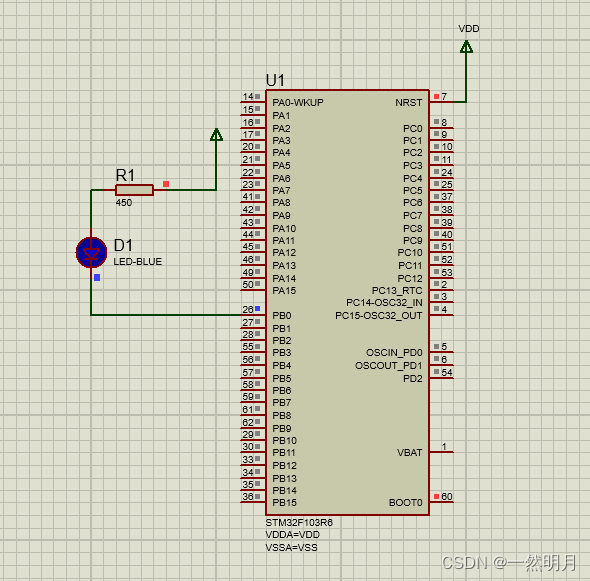
STM32-电灯,仿真
目录 1.配置vscode 2.新创建软件工程 3.仿真 4.源码 5.运行效果 1.配置vscode http://t.csdnimg.cn/BvCLx 安装 C/C Extension Pack 安装 Embedded IDE 安装 Keil MDK 配置路径 2.新创建软件工程 下拉找到对应的 输入项目名字,选择项目所在文件夹即可 3.仿真 一路新…...

《SpringBoot》系列文章目录
SpringBoot是由Pivotal团队提供的全新框架,旨在简化新Spring应用的初始搭建以及开发过程。以下是一些关于SpringBoot的详细介绍: 设计目的:SpringBoot通过特定的方式来进行配置,使得开发人员不再需要定义样板化的配置,…...

牛客小白月赛94VP
1.签到:https://ac.nowcoder.com/acm/contest/82957/A 下面是AC代码: #include<bits/stdc.h> using namespace std; map<int,int> mp; int main() {for(int i1;i<9;i){int x;cin>>x;mp[i]x;}string s;cin>>s;s s;for(int i…...

php 亚马逊AWS-S3对象存储上传文件
最近做国外项目的时候,需要把文件上传到AWS-S3对象存储空间里,下面整理一下上传方法,和碰到的问题 代码 /*** 亚马逊oss Aws上传* composer require aws/aws-sdk-php* param $filePath* param $ossPath* return array* author wzb* data 202…...

electron-01 基础及NPM相关配置
electron基础 结构 ChromiumNode.jsNative apis 工作流程 启动APP主进程创建windowWin加载界面操作 主进程 package.json中main属性对应的文件一个应用对应一个主进程只有主进程可以进行GUI的API操作 渲染进程 windows中展示的界面通过渲染进程表现一个应用可以有多个渲…...

Foxit PDF Editor Pro福昕PDF编辑器Pro:重塑您的文档编辑体验
在信息爆炸的时代,PDF文件因其跨平台、格式稳定等特性,成为我们日常工作与学习中不可或缺的一部分。然而,面对这些文件时,许多人都会遇到一个共同的难题:如何高效、专业地编辑PDF内容?今天,我要…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
