二进制中1的个数c++
题目描述
计算鸭给定一个十进制非负整数 NN,求其对应 22 进制数中 11 的个数。
输入
输入包含一行,包含一个非负整数 NN。(N < 10^9)
输出
输出一行,包含一个整数,表示 NN 的 22 进制表示中 11 的个数。
样例输入
100
样例输出
3
分析
这道题首先要把一个十进制整数转化为二进制数
在转化过程中判断是否是一,如果是,那么+1
代码如下:
#include<bits/stdc++.h>
using namespace std;
int main(){long long n,sum=0;cin>>n;while(n!=0){if(n%2==1){sum++;}n=n/2;}cout<<sum;return 0;
}
相关文章:

二进制中1的个数c++
题目描述 计算鸭给定一个十进制非负整数 NN,求其对应 22 进制数中 11 的个数。 输入 输入包含一行,包含一个非负整数 NN。(N < 10^9) 输出 输出一行,包含一个整数,表示 NN 的 22 进制表示中 11 的个数。 样例输入 100 …...

【面试干货】数据库乐观锁,悲观锁的区别,怎么实现
【面试干货】数据库乐观锁,悲观锁的区别,怎么实现 1、乐观锁,悲观锁的区别2、总结 💖The Begin💖点点关注,收藏不迷路💖 1、乐观锁,悲观锁的区别 悲观锁(Pessimistic Lo…...
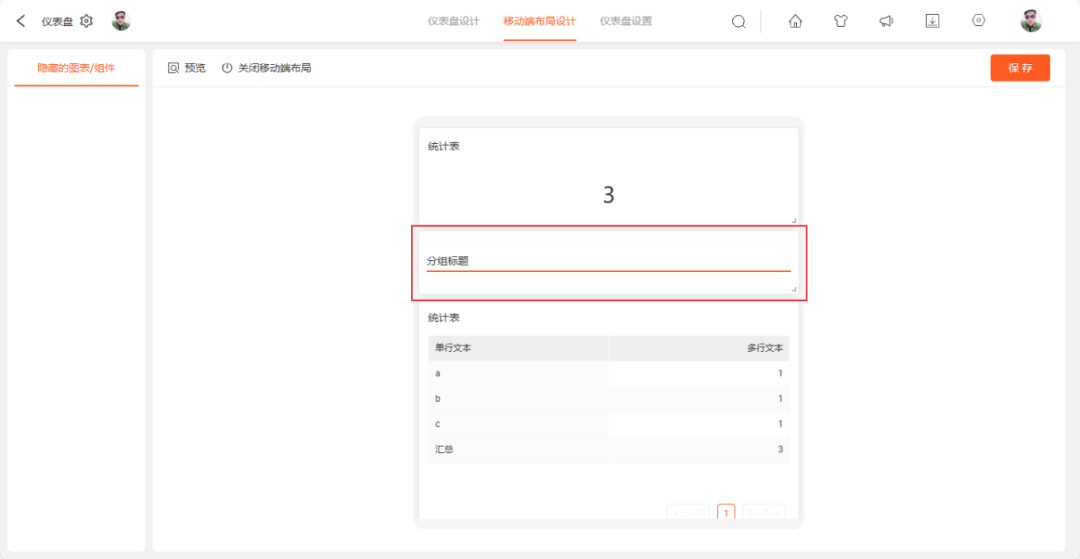
移动端仪表盘,支持更多组件
05/22 主要更新模块概览 定位函数 快捷筛选 轨迹图表 时间组件 01 表单管理 1.1 【表单组件】- 表单关联新增支持自定义按钮样式 说明: 表单关联-关联数据按钮,原仅支持默认按钮样式,现增加关联数据按钮自定义功能,满…...

科技产业园3D探秘:未来科技之城的奇幻之旅
在数字时代的浪潮中,科技产业园区成为了推动城市经济发展、科技创新的重要引擎。 当我们打开科技产业园的3D可视化模型,仿佛穿越时空,来到了一个充满奇幻色彩的科技世界。在这里,高楼大厦鳞次栉比,绿色植被点缀其间&am…...
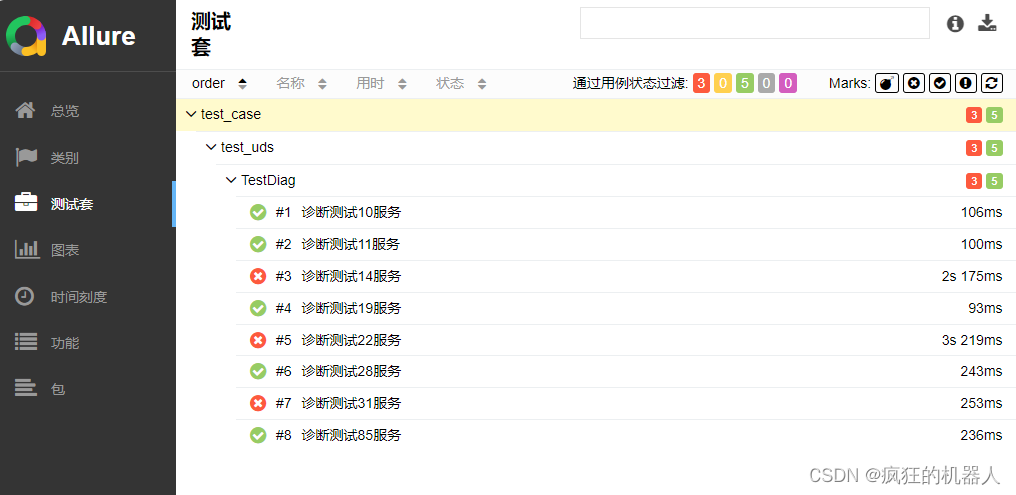
【Python搞定车载自动化测试】——Python基于Pytest框架实现UDS诊断自动化(含Python源码)
系列文章目录 【Python搞定车载自动化测试】系列文章目录汇总 文章目录 系列文章目录💯💯💯 前言💯💯💯一、环境搭建1.软件环境2.硬件环境 二、目录结构三、源码展示1.诊断基础函数方法2.诊断业务函数方法…...

探索SPI单线传输模式中时钟线与数据传输的简化
探索SPI单线传输模式:时钟线与数据传输的简化之道 在当今的嵌入式系统和微控制器通信中,串行外设接口(SPI)因其高速、全双工和同步的特点而广受欢迎。然而,随着设备尺寸和复杂性的不断减少,对SPI通信的简化…...

使用FFmpeg推流实现在B站24小时点歌直播
使用FFmpeg推流实现在B站24小时点歌直播 本文首发于个人博客 安装FFmpeg centos7 https://www.myfreax.com/how-to-install-ffmpeg-on-centos-7/ https://linuxize.com/post/how-to-install-ffmpeg-on-centos-7/ 使用FFmpeg在B站直播 https://zhuanlan.zhihu.com/p/2395…...

汽车防抱死制动系统ABS的单片机程序Proteus仿真设计
次设计对汽车防抱死系统进行简单的设计,针对车速、轮速两个信号进行分析,并根据最佳滑移率计算。采用对比实时滑移率对比分析,ECU控制制动器进行制动力调节使滑移率在制动过程处于最佳范围,保证系统具有良好制动性能。 汽车的制动液压调节器主要包含以下几个部件:调压电磁…...
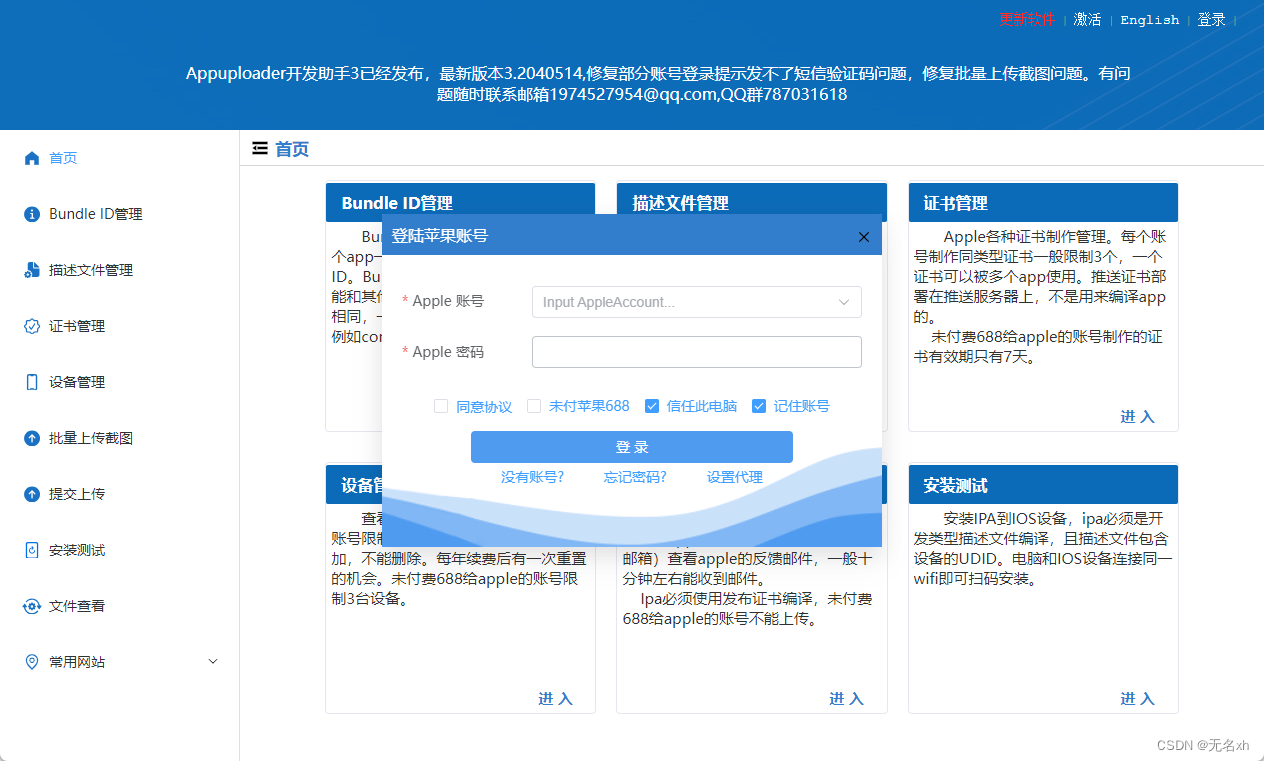
IOS开发者证书快捷申请
App Uploader 在进行iOS应用开发中,可以借助appuploader辅助工具进行证书制作、上传和安装测试等操作。首先,您需要访问官方网站获取最新版本的appuploader。最新版本已经优化了与Apple账号的登录流程,无需支付688元,并提供了Windows版和Mac版供用户选择。下载完成后,解压…...

python 火焰检测
在日常生活,总是离不开火,有时候我们需要预防火灾发生,但是我们又不可能一直盯着,这时候我们就需要一款程序帮我们盯着,一旦发生火灾从而告知我们,今天就带大家编写这么一款应用。 安装需要的库 pip install opencv-python 代码实现 import cv2 # Library for…...

栈——顺序存储
#include<stdio.h> #define MaxSize 10 //栈的所有操作时间复杂度都是O(1) //定义 typedef struct{int data[MaxSize];int top; //栈顶指针,永远指向栈顶元素 }SqStack;//初始化,使栈顶指针指向-1 void InitStack(SqStack &S){S.top-1; }…...
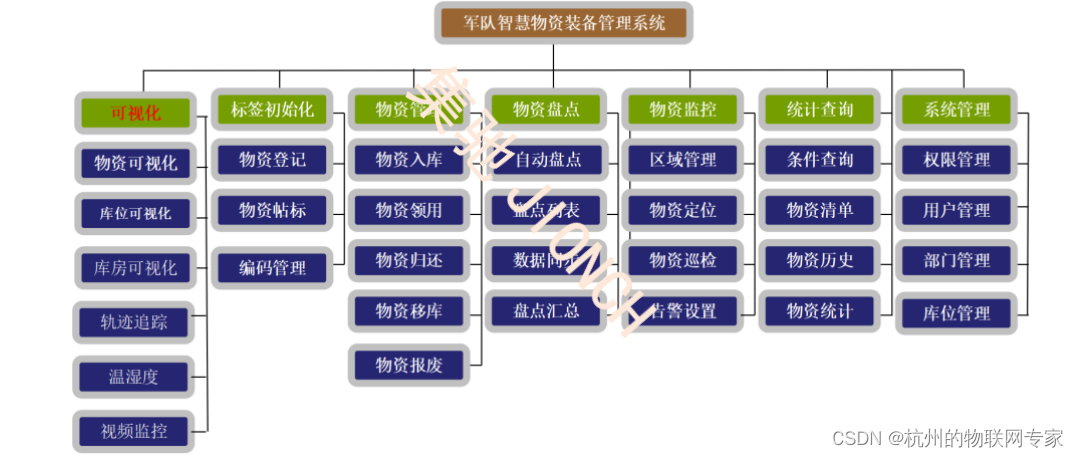
军队仓库管理系统|DW-S301系统特点
部队仓库管理系统DW-S301系统通过数据采集、互联网和物联网技术,实现数字化智能管控,以提高军用物资的仓储准确率和流转率,缩短周转时间,降低库存成本,也有助于消除生产过程中的不确定性。 系统功能:通过部…...

MySQL和MongoDB数据库的区别
MySQL和MongoDB数据库的区别 随着大数据和云计算技术的兴起,数据库的选择成为开发者和架构师必须面对的重要决策。MySQL和MongoDB作为关系型数据库和非关系型数据库的代表,在各自领域都有着广泛的应用。本文将从多方面详细比较MySQL和MongoDB࿰…...

类脑计算和量子计算、人工智能的关系
According to www.iAsk.ai Ask Ai Search Engine: 类脑计算、量子计算和人工智能是三个不同但相关的领域。它们在不同层面上探索和利用了不同的计算模型和技术,但都旨在推动计算能力的发展和创新。 类脑计算是一种受到人脑神经系统启发的计算模型。它试图通过模拟…...
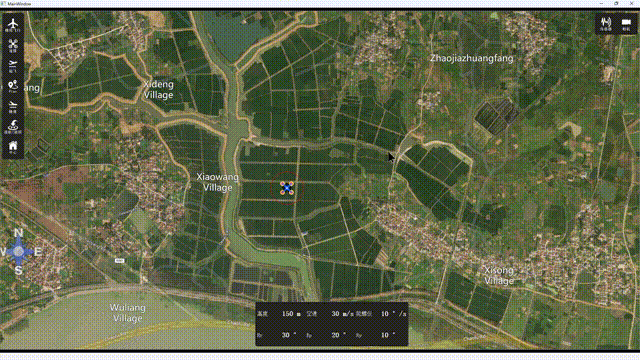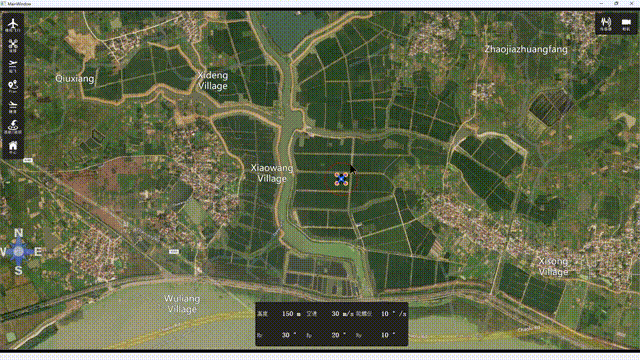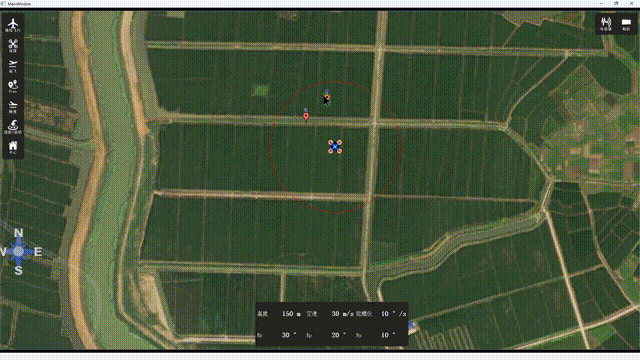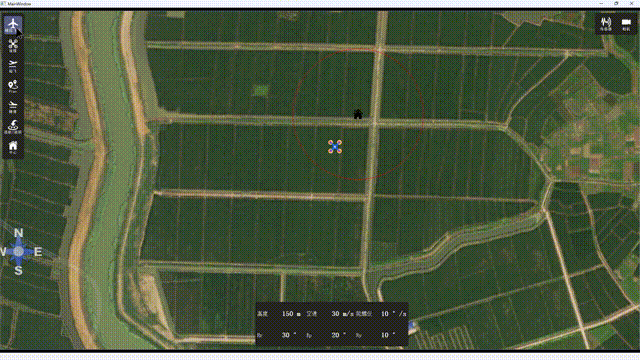
Qt5 互动地图,实现无人机地面站效果
一、概述 本文主要通过Qt5opmapcontrol实现一个简单的无人机地面站效果。opmapcontrol是一个比较古老的QT开源地面站库,可选择谷歌地图,必应地图, 雅虎地图,GIS等。可直接使用源码,也可以编译生成库进行调用。实现效果…...

【文末附gpt升级方案】TikTok Symphony AI套件:智能视频制作的新篇章
TikTok Symphony AI套件:智能视频制作的新篇章 摘要 随着短视频平台的兴起,视频内容的创作与制作已成为品牌方吸引用户、传递信息的重要手段。TikTok作为全球领先的短视频平台,近日宣布推出Symphony AI套件,旨在通过人工智能技术…...

面试回答——有高并发、高性能、高可用系统架构设计实践以及性能调优经验
🌈hello,你好鸭,我是Ethan,一名不断学习的码农,很高兴你能来阅读。 ✔️目前博客主要更新Java系列、项目案例、计算机必学四件套等。 🏃人生之义,在于追求,不在成败,勤通…...

rocketmq初识
package com.ldj.rocketmq.producer;import org.apache.rocketmq.client.producer.DefaultMQProducer; import org.apache.rocketmq.common.message.Message;import java.nio.charset.StandardCharsets;/*** User: ldj* Date: 2024/3/26* Time: 2:26* Description: 单向消息生产…...

php 使用phpoffice导出导出excel
荆轲刺秦王 在PHP中,可以使用 PhpSpreadsheet 库来创建和导出Excel文件。PhpSpreadsheet 是一个纯PHP 编写的组件库,它使用现代 PHP 写法,代码质量和性能比 PHPExcel 高不少,完全可以替代PHPExcel(PHPExcel已不再维护…...

安装docker版elasticsearch和kibana
本文将介绍用docker的方式安装elasticsearch和kibana,并用浏览器访问elasticsearch。这里的elasticsearch主要给测试环境使用,因此不会设置https和密码。kibana是elasticsearch的前端,可以用来访问elasticsearch,展示数据图表、搜…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
