二叉树的链式实现
目录
一、二叉树的基础操作
二、二叉树代码图解
2.1 遍历
2.2 求大小
2.3 创建与销毁
2.4 与队列结合解决问题
三、二叉树C语言源码汇总
二叉树的代码实现运用了函数递归的思想,了解函数递归的知识请见博主的另一篇博客:
http://t.csdnimg.cn/PoMtd
一、二叉树的基础操作
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data; // 当前结点值域 struct BinaryTreeNode* left; // 指向当前节点左孩子struct BinaryTreeNode* right; // 指向当前节点右孩子
}BTNode;//创建二叉树
BTNode* CreatBinaryTree();
//前序遍历
void PrevOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后序遍历
void PostOrder(BTNode* root);
//结点个数
int TreeSize(BTNode* root);
//叶子结点个数
int TreeLeafSize(BTNode* root);
//二叉树高度
int TreeHeight(BTNode* root);
//二叉树第k层结点个数
int TreeLevelKSize(BTNode* root, int k);
//二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, int x);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* CreateTree(char* a, int* pi);
//二叉树的销毁
void BinaryTreeDestory(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
//层序遍历
void TreeLevelOrder(BTNode* root);二、二叉树代码图解
2.1 遍历
详见博主的另一篇博客:http://t.csdnimg.cn/YnlIr
2.2 求大小
详见博主的另一篇博客:http://t.csdnimg.cn/Ce2Fs
2.3 创建与销毁
详见博主的另一篇博客:http://t.csdnimg.cn/LXt8P
2.4 与队列结合解决问题
详见博主的另一篇博客:http://t.csdnimg.cn/zbNis
三、二叉树C语言源码汇总
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
//手动造树(测试用)
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);BTNode* node7 = BuyNode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node5->right = node7;return node1;
}
//前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
//结点个数
int TreeSize(BTNode* root)
{if (root == NULL){return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子结点个数
int TreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);}
//二叉树高度
int TreeHeight(BTNode* root)
{if (root == NULL){return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}
//求第K层的节点数目
int TreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}
//查找值为x的节点
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* ret1 = TreeFind(root->left, x);if (ret1){return ret1;}BTNode* ret2 = TreeFind(root->right, x);if (ret2){return ret2;}return NULL;
}
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* CreateTree(char* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc");exit(1);}root->data = a[(*pi)++];root->left = CreateTree(a, pi);root->right = CreateTree(a, pi);return root;
}
//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{//判空if (root == NULL){return NULL;}//释放左子树BinaryTreeDestory(root->left);//释放右子树BinaryTreeDestory(root->right);//释放本身结点free(root);
}
//层序遍历
void TreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (QueueEmpty(&q)==false){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}QueueDestroy(&q);
}
//判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root != NULL){QueuePush(&q, root);}//入队遇到空停止入队while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//判断后面是否还有非空while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){return false;}}QueueDestroy(&q);return true;
}相关文章:

二叉树的链式实现
目录 一、二叉树的基础操作 二、二叉树代码图解 2.1 遍历 2.2 求大小 2.3 创建与销毁 2.4 与队列结合解决问题 三、二叉树C语言源码汇总 二叉树的代码实现运用了函数递归的思想,了解函数递归的知识请见博主的另一篇博客: http://t.csdnimg.cn/Po…...

STM32中断编程入门
文章目录 一、 理论部分1.中断系统2.中断执行流程3.NVIC的基本结构4.EXTI介绍5.AFIO复用IO口 二、实验目的:学习stm32中断原理和开发编程方法。使用标准完成以下任务:(一)实验一 开关控制LED的亮灭1.代码部分2.运行结果 ÿ…...

《我的阿勒泰》读后感
暂没时间写,记录在此,防止忘记,后面补上!!! 【经典语录】 01、如果天气好的话,阳光广阔地照耀着世界,暖洋洋又懒洋洋。这样的阳光下,似乎脚下的每一株草都和我一样,也把身子完全舒展开了。 02、…...

Android.mk简单介绍、规则与基本格式
文章目录 Android.mk与makefile区别Android.mk规则Android.mk基本格式 Android.mk与makefile区别 Android.mk 和 Makefile 都是用于构建代码项目的构建脚本文件,但是它们在特定上下文中有一些区别: Android.mk: Android.mk 是用于构建 Android 应用或库…...
-MVCC多版本管理)
【MySQL精通之路】InnoDB(3)-MVCC多版本管理
InnoDB是一个多版本(MVCC)的存储引擎。 它保留有关更改行的旧版本的信息,以支持事务性功能,如并发和回滚。 这些信息存储在称为回滚段的数据结构中的Undo表空间中。 参见“Undo表空间”。 InnoDB使用回滚段(rollback…...
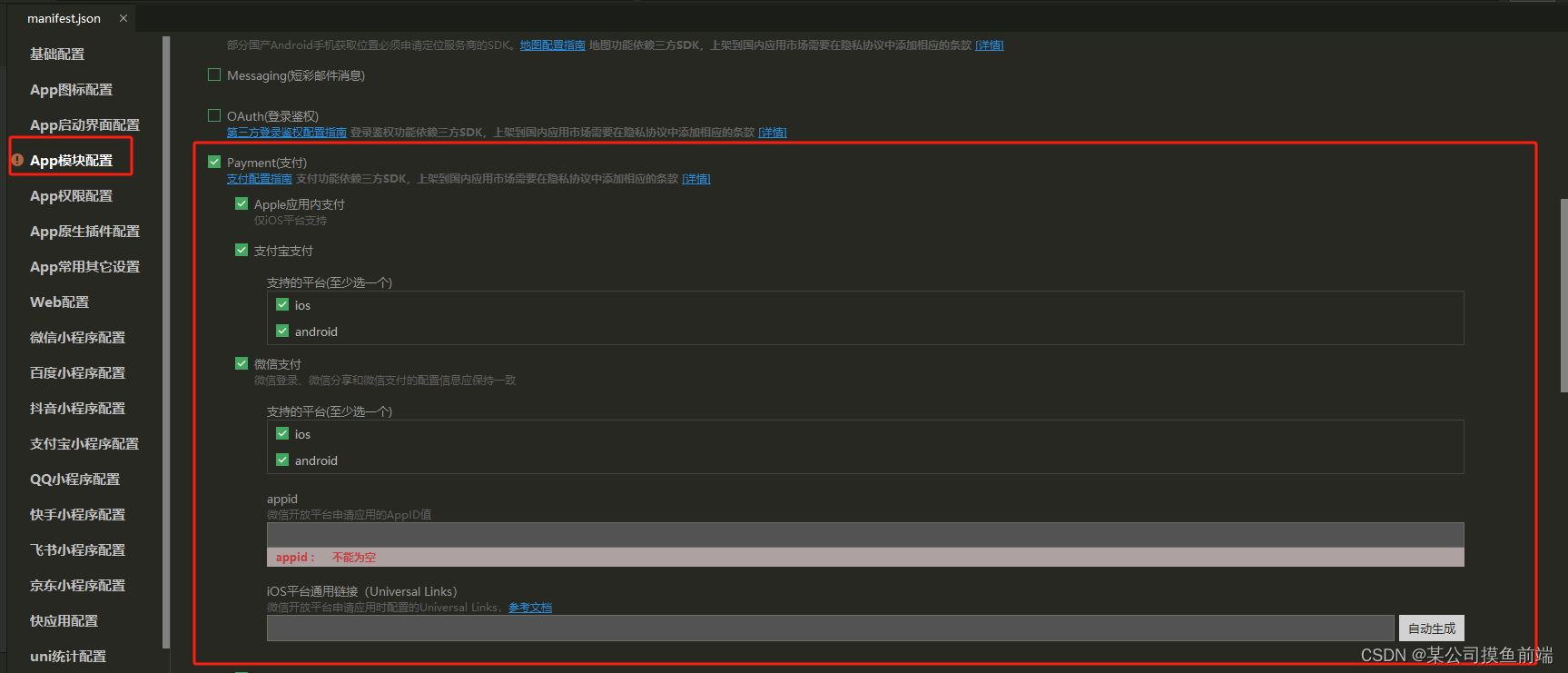
uniapp 对接 微信App/支付宝App 支付
相关文档:uni.requestPayment(OBJECT) | uni-app官网 示例代码: import qs from qsasync aliPay(){const { provider } await uni.getProvider({ service:payment })if(provider.includes(alipay)){uni.request({url:后端接口地址,data:{ //传参 },suc…...

cmake配置opencv与boost库
Cmake配置外部依赖库(以Opencv和Boost为例) Cmake对于外部依赖库,需要知道外部库的头文件路径,库文件路径以及库的名字。比如,对于要使用的Boost库,需要知道头文件的位置,库目录的位置以及库依…...

【Kotlin 一】Kotlin入门知识简介、变量声明、数字类型
1. Kotlin简介 Kotlin旨在解决 Java语言在编码效率和代码质量上存在的问题,并且与Java语言完全兼容。Kotlin通过简化语法、提供更强大的函数以及减少样本代码的编写,使开发者能够更高效地编写代码。Kotlin适用于Android、Web后端开发等多种场景 2.Kotl…...
)
Java 微信小程序登录(openId方式)
1 需求 在开发微信小程序项目时,登录采用的是openId方式,这是一种用户无感的登录方式,用户点开微信小程序时,去调用后端的登录接口。 核心代码 Slf4j Component public class WeChatUtil {private static final String …...

为何程序员35岁就开始被嫌弃了?程序员该如何避免中年危机?
文章目录 一、为何程序员35岁就开始被嫌弃了?1、技术更新迅速2、职业发展瓶颈3、成本考虑4、年龄歧视5、市场供需变化6、个人因素 二、程序员该如何避免中年危机?1、持续学习与技能更新2、拓展技术广度与深度3、提升软技能4、关注行业趋势与市场变化5、建…...
【2024软考】史上最全!软考刷题+解析大合集(9万字全手工打,货真价实)
计算机基础知识 1.中断向量表用来保存各个中断源的中断服务程序的入口地址。当外设发出中断请求信号(INTR)以后,由中断控制器(INTC)确定其中断号,并根据中断号查找中断向量表来取得其中断服务程序的入口地…...

【Spring Security + OAuth2】授权
Spring Security OAuth2 第一章 Spring Security 快速入门 第二章 Spring Security 自定义配置 第三章 Spring Security 前后端分离配置 第四章 Spring Security 身份认证 第五章 Spring Security 授权 第六章 OAuth2 文章目录 Spring Security OAuth21、基于request的授权1…...

失落的方舟台服预下载教程 一键下载+账号注册教程
失落的方舟台服预下载教程 一键下载+账号注册教程 是一款今年备受瞩目的游戏,将于5月30日正式上线,这款游戏搭建在虚幻引擎的基础上,为玩家们带来了极佳的视觉体验。这款游戏秉承着MMO类型游戏一贯的玩法,但是制作组在…...

【启明智显技术分享】SOM2D02-2GW核心板适配ALSA(适用Sigmastar ssd201/202D)
提示:作为Espressif(乐鑫科技)大中华区合作伙伴及sigmastar(厦门星宸)VAD合作伙伴,我们不仅用心整理了你在开发过程中可能会遇到的问题以及快速上手的简明教程供开发小伙伴参考。同时也用心整理了乐鑫及星宸…...

人工智能的发展现状,AI将如何改变IT行业,哪些职业将最先失业
文章目录 一、人工智能的发展现状1、技术进展与突破2、商业应用与市场3、挑战与问题4、未来趋势 二、AI将如何改变IT行业1、工作方式的转变:2、未来发展的推动:3、用户服务和体验的提升:4、创新和转型的推动:5、融入日常生活和工作…...

request.js使用Promise.all等待所有请求完成再进行数据赋值
在JavaScript中,使用request.js发送多个并发请求,并使用Promise.all来处理这些请求的结果可以通过以下方式实现: 首先,确保你已经安装了request.js,如果没有,可以通过npm安装: npm install re…...
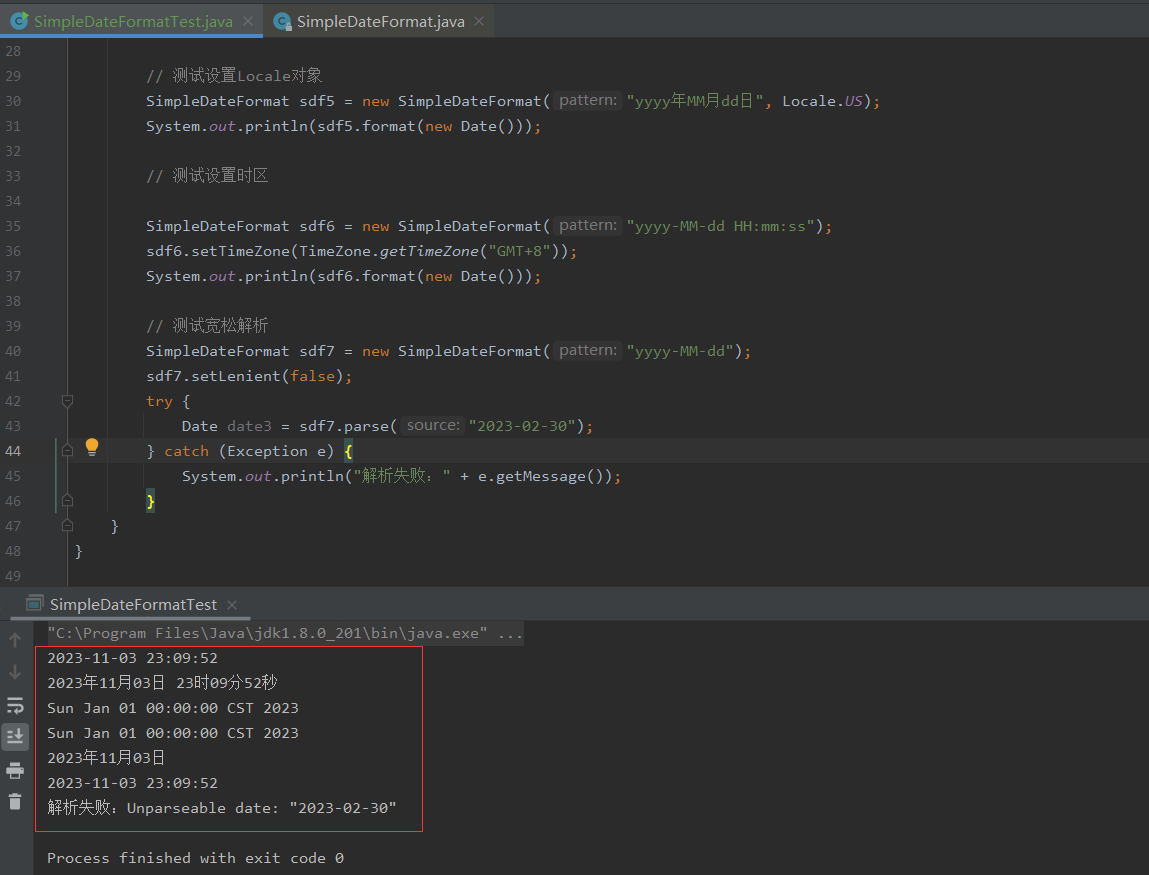
Java开发者必知的时间处理工具:SimpleDateFormat类详解
哈喽,各位小伙伴们,你们好呀,我是喵手。运营社区:C站/掘金/腾讯云;欢迎大家常来逛逛 今天我要给大家分享一些自己日常学习到的一些知识点,并以文字的形式跟大家一起交流,互相学习,一…...

构造函数的用法
c 子类构造函数初始化及父类构造初始化_构造函数对父类进行初始化-CSDN博客...

环形链表Ⅱ-力扣
第一种解法时哈希表,set在使用insert插入时,会返回一个pair,如果pair的值为0,则插入失败,那么返回这个插入失败的节点,就是入环的第一个节点,代码如下: /*** Definition for singly…...

【microros】解决 microros安装过程中的 undefined reference to `fmt::v6 问题
目录 问题解决方案参考链接 问题 在 ubuntu-20 arm 开发板上根据官方文档手动编译安装 microros 过程中,执行 ros2 run micro_ros_setup build_agent.sh 命令时,遇到了 undefined reference to fmt::v6 的问题,大概报错如下: Yo…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
