Topk问题以及二叉树的三种层序遍历和基本操作
一、Topk问题
1、问题描述
2、思路
3、代码实现
首先通过文件函数生成100000个数据:
void CreateNDate()
{// 造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose(fin);
}在前面我们了解到若为向下建堆则为O(N);而向上建堆为O(N*logN);所以我们在这采用向下建堆:
void AdjustDown(HPDataType* a, int n, int parent)
{// 先假设左孩子小int child = parent * 2 + 1;while (child < n) // child >= n说明孩子不存在,调整到叶子了{// 找出小的那个孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void TestHeap3()
{int k;printf("请输入k>:");scanf("%d", &k);int* kminheap = (int*)malloc(sizeof(int) * k);//开辟空间if (kminheap == NULL){perror("malloc fail");return;}const char* file = "data.txt";//打开我们刚刚创建的文件FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;}// 读取文件中前k个数for (int i = 0; i < k; i++){fscanf(fout, "%d", &kminheap[i]);}// 建K个数的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(kminheap, k, i);}// 读取剩下的N-K个数int x = 0;while (fscanf(fout, "%d", &x) > 0){if (x > kminheap[0]){kminheap[0] = x;//堆顶数据始终是最小的不可能出现卡住数据进不去问题AdjustDown(kminheap, k, 0);}}printf("最大前%d个数:", k);for (int i = 0; i < k; i++){printf("%d ", kminheap[i]);}printf("\n");
}
二、二叉树的三种层序遍历
以下三种遍历,如果树的深度太深就会栈溢出。
1、二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf(" null ");return;}printf("%d ", root->_data);PreOrder(root->_left);PreOrder(root->_right);
}递归调用图: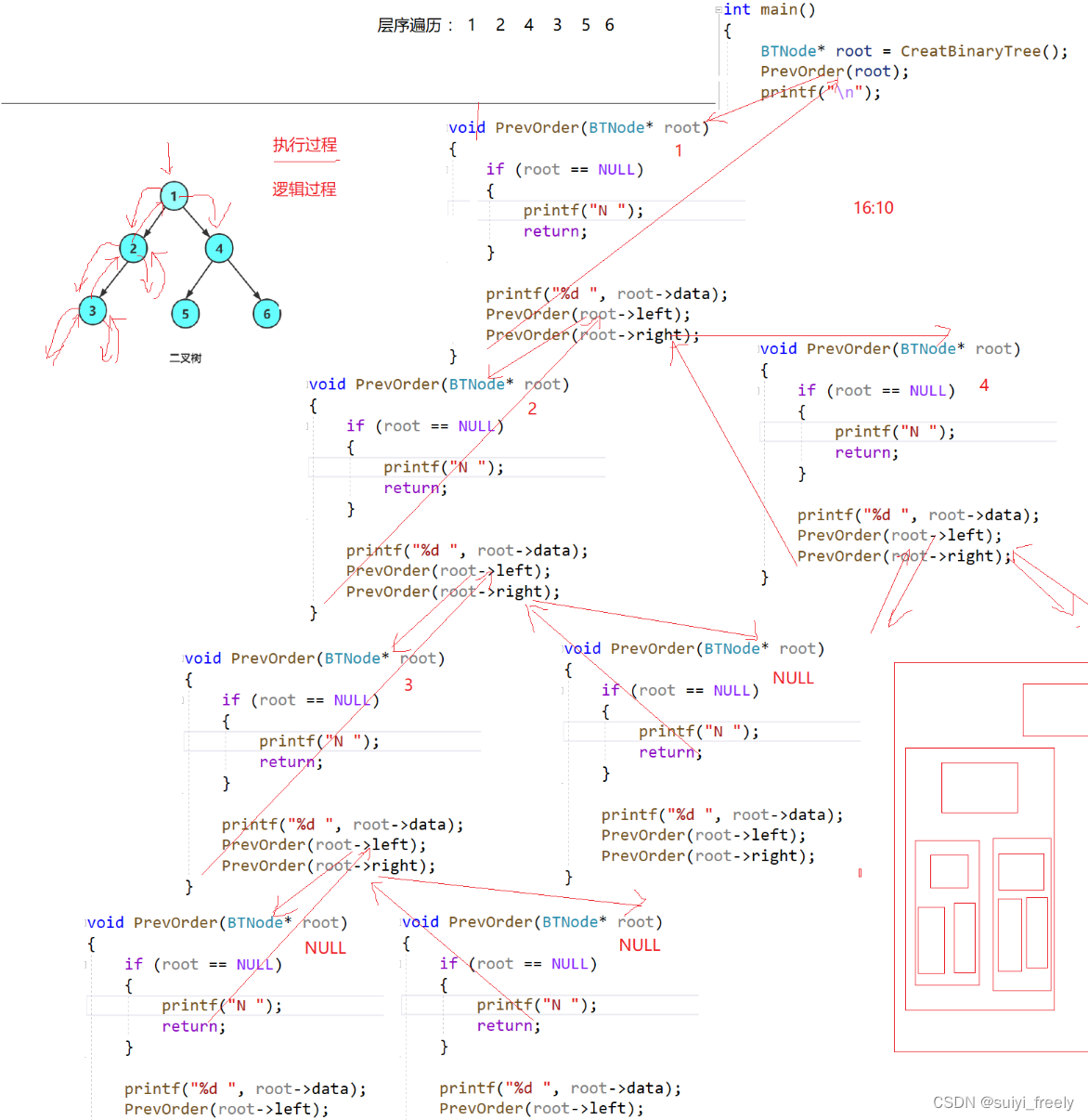
剩下的两种遍历流程图与其类似,这里不做详细图解。
2、二叉树中序遍历
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf(" null ");return;}InOrder(root->_left);printf("%d ", root->_data);InOrder(root->_right);
}3、二叉树的后序遍历
// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf(" null ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%d ", root->_data);
}三、树相关的计算
1、节点数的计算
节点数的计算可分为左树+右树 +1;
int treesize(BTNode* root)
{if (root == NULL) {return 0;}return treesize(root->_left) + treesize(root->_right);
}2、叶字节点数
为空,叶为0,非空为左叶子数+右叶子数,结束条件为该节点左右两个子节点为空,或者该节点为空
int treeleaf(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return treeleaf(root->_left) + treeleaf(root->_right);
}3、深度
若为空则高度为0,非空为左数高度与右数高度大的那一个
int treeleafhigh(BTNode* root)
{if (root == NULL){return 0;}int lefthigh = treeleafhigh(root->_left) + 1;int righthigh = treeleafhigh(root->_right) + 1;if (lefthigh > righthigh){return lefthigh;}else{return righthigh;}
}相关文章:

Topk问题以及二叉树的三种层序遍历和基本操作
一、Topk问题 1、问题描述 TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。 比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。 2、思路 对于Top-K问题,能想到的最简单直接的…...

深度学习设计模式之桥接模式
文章目录 前言一、介绍二、详细分析1.核心组成2.实现步骤3.代码示例4.优缺点优点缺点 5.使用场景 总结 前言 桥接模式是将抽象部分与实现部分分离,使它们都可以独立的变化。 一、介绍 桥接模式是结构型设计模式,主要是将抽象部分与实现部分分离&#x…...
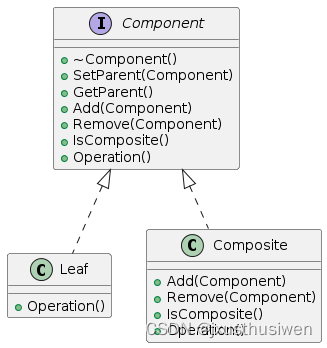
设计模式 17 组合模式 Composite Pattern
设计模式 17 组合模式 Composite Pattern 1.定义 组合模式(Composite Pattern),又叫部分整体模式,是用于把一组相似的对象当作一个单一的对象。组合模式依据树形结构来组合对象,用来表示部分以及整体层次。这种类型的设…...

【经典论文阅读10】MNS采样——召回双塔模型的最佳拍档
这篇发表于2020 WWW 上的会议论文,提出一种MNS方式的负样本采样方法。众所周知,MF方法难以解决冷启动问题,于是进化出双塔模型,但是以双塔模型为基础的召回模型的好坏十分依赖负样本的选取。为了解决Batch内负样本带来的选择性偏差…...
介绍)
串行低功耗芯片间媒体总线(SLIMbus)介绍
文章目录 SLIMbus简介slimbus设备和设备类Manager DeviceFramer DeviceInterface DeviceGeneric Device (Function)SLIMbus组件简单的SLIMbus组件复杂的SLIMbus组件SLIMbus的DATA和CLKSLIMbus的Clock Frequencies和GearsCells, Slots, Subframes, Frames, and...

esp32-S3 使用自带的大模型,实现本地文字转语言tts
目录 CMakeLists.txt文件中: 初始化以及实际运用代码: 在partitions.csv 内存分配文件中,添加voice_data项...
)
Redis事务(1)
什么是事务? Redis 的事务和 MySQL 的事务概念上是类似的. 都是把⼀系列操作绑定成⼀组. 让这⼀组能够批量执行。 但是注意体会 Redis 的事务和 MySQL 事务的区别: 弱化的原⼦性: redis 没有 “回滚机制”. 只能做到这些操作 “批量执⾏”. 不能做到 “⼀个失败就…...
等级考试试卷(四级))
202206青少年软件编程(Python)等级考试试卷(四级)
第 1 题 【单选题】 有如下 Python 程序, 包含 lambda 函数, 运行该程序后, 输出的结果是? ( ) g = lambda x,y:x*yprint(g(2,3))A :2 B :3 C :6 D :8 正确答案:C 试题解析: g = lambda x, y: x*y, lambda 函数返回参数 x 和 y 的积, 因此选 C。 第 2 题 【单选…...
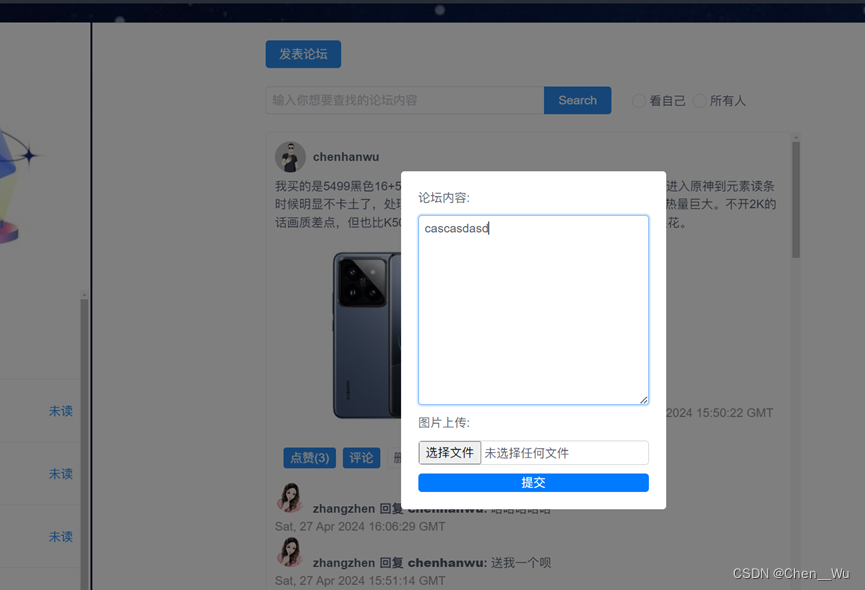
大作业爬取手机数据,实现手机推荐系统以及朋友圈手机论坛
1、功能简介 (1)用户注册与用户登录 (2)手机搜索、手机比拼、手机个性化推荐 (3)点击搜索的手机图片会就用户行为,轮播展示用户行为,推荐点击次数靠前的手机 (4…...

Leetcode 环形链表|| 快慢指针解法
但是我们不知道 aaa 的值,该怎么办?依然是使用双指针法。考虑构建一个指针,此指针需要有以下性质:此指针和 slow 一起向前走 a 步后,两者在入口节点重合。那么从哪里走到入口节点需要 aaa 步?答案是链表头节…...

出书,是「盖你自己的房子」你知道吗?
出书是「盖你自己的房子」 尊敬的出书盟友: 你好!我希望这封信能够激发您对出书和阅读的热情。 在当今信息爆炸的时代,每个人都有机会分享自己的故事、思想和知识。而书籍作为一种流传百年的媒体,依旧承载着无限的力量和影响力…...

深入探索MySQL SELECT查询:从基础到高级,解锁数据宝藏的密钥
系列文章目录 更新ing... MySQL操作全攻略:库、表、数据、事务全面指南深入探索MySQL SELECT查询:从基础到高级,解锁数据宝藏的密钥MySQL SELECT查询实战:练习题精选,提升你的数据库查询技能PyMySQL:连接P…...

驾校管理系统-手把手调试搭建
驾校管理系统-手把手调试搭建 驾校管理系统-手把手调试搭建...

知能行——考研数学利器
知能行使用体验全记录 首先,我先介绍一下自己,我是2018级的,2022年6月毕业,本科沈阳工业大学(双非),今年二战,专业课自动控制原理,数二英二,目标是江南大学控…...

pod 库发布脚本
repo_tag.sh 文件 #!/bin/zsh# 私有库名称 #PODNAME${PWD##*/} PODNAME"LBHorizontalCenterLayout"function obtain_git_tag {# 类似 "s.version 0.0.1"VERSION_STRINGgrep -E s.version.* ${PODNAME}.podspecTAGtr -cd "[0-9.]" <<&…...

Java 8 新特性:深入理解 Lambda 表达式的强大与应用
Java 8 新特性:深入理解 Lambda 表达式的强大与应用 Lambda 表达式是 Java 8 引入的重要特性之一,它允许将匿名函数(即无名称的函数)作为参数传递给方法,简化了代码的编写,使代码更加简洁和易读。本文将深…...

HTML5 Canvas图形绘制技术应用
HTML5 Canvas图形绘制技术应用 目录 Canvas基础知识基本绘图操作路径操作文本绘制图像绘制变换复合图形与剪切阴影渐变动画与交互高级技巧...
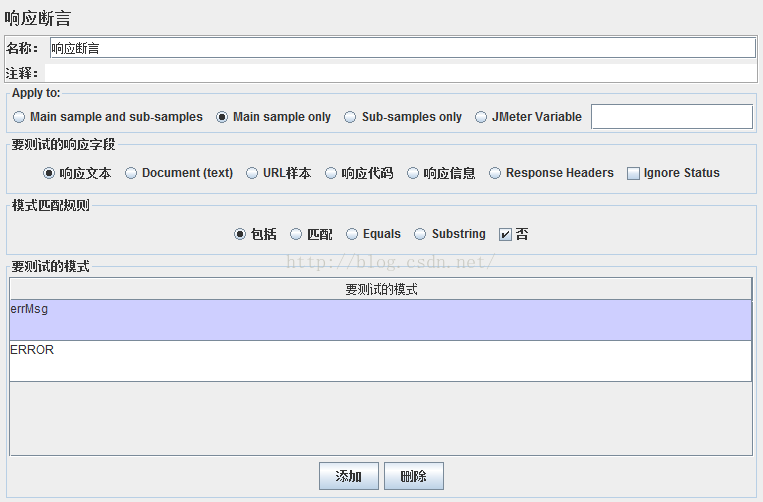
JMETER工具:以录制手机app为例
JMETER工具:以录制手机app为例子 JMETER安装和环境配置 pc需要安装jdk,并进行jdk的环境配置,安装好jdk并配置好后,通过命令行输入java –version出现以下界面就表示安装成功: (对应的jdk版本不可太低&…...

PDF文件权限密码保护:如何去除及解决方法
如果你忘记了PDF文件密码,不用担心!PDF解密、找回密码、去除密码的方法简单易行。只需两步:1、打开百度搜索“密码帝官网”;2、在官网页面点击“立即开始”,上传文件,稍等片刻即可找回密码。这种方法安全、…...
】电子通信创新创业教育综合)
【电子信息(工程)】电子通信创新创业教育综合
电子通信创新创业教育 阐述电磁场、电磁波和电磁频谱及应用一、电磁场 法拉第根据电流与磁场的关系,提出了电磁感应定律:如果电磁场中有处于运动状态下的闭合回路导体存在,流经该导体磁场的磁场强度和磁场量,通常都会出现相应的变化,电磁感应电流由此而产生。随后,英国的…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...