Rust面试宝典第14题:旋转数组
题目
给定一个数组,将数组中的元素向右移动k个位置,其中k是非负数。要求如下:
(1)尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
(2)使用时间复杂度为O(n)和空间复杂度为O(1)的原地算法解决这个问题。
示例 1:
输入: [1, 2, 3, 4, 5, 6, 7] 和 k = 3输出: [5, 6, 7, 1, 2, 3, 4]解释:向右旋转1步: [7, 1, 2, 3, 4, 5, 6]向右旋转2步: [6, 7, 1, 2, 3, 4, 5]向右旋转3步: [5, 6, 7, 1, 2, 3, 4]示例 2:
输入: [-8, -100, 50, 66] 和 k = 2输出: [50, 66, -8, -100]解释:向右旋转1步: [66, -8, -100, 50]向右旋转2步: [50, 66, -8, -100]
解析
这道题主要考察应聘者从多个角度、多个维度分析和思考问题的能力。
最直接、最简单的解决方案当然是“暴力法”,也就是每次将数组向右移动一个元素,一共旋转k次。向右移动一个元素,需要将最后一个元素移动到数组开头,然后将其他元素依次右移。“暴力法”的时间复杂度为O(n*k),空间复杂度为O(1)。具体实现,可参考下面的示例代码。这里,我们使用了Rust标准库中的rotate_right方法,它直接提供了按指定步数向右旋转数组的功能,使得代码更为简洁。
fn rotate_array(arr: &mut [i32], mut k: usize) {let n_len = arr.len();k %= n_len;arr.rotate_right(k);
}fn print_array(arr: &[i32]) {for &item in arr.iter() {print!("{} ", item);}println!();
}fn main() {let mut data = [1, 2, 3, 4, 5, 6, 7];rotate_array(&mut data, 3);print_array(&data);
}“暴力法”的时间复杂度较高,我们可以通过以空间换时间的方式来优化时间复杂度。具体做法为:使用一个额外的数组来将每个元素放到正确的位置上,也就是我们把原本数组里下标为i的元素,放到(i+k)%数组长度的位置;最后,我们把新的数组拷贝到原来的数组中。该方法的时间复杂度为O(n),空间复杂度也为O(n)。具体实现,可参考下面的示例代码。这里,我们使用to_vec()方法来创建原数组的一个拷贝,然后通过索引操作和copy_from_slice()方法来完成数据的转移。
fn rotate_array(arr: &mut [i32], k: usize) {let n_len = arr.len();let mut data_bak = arr.to_vec();for i in 0..n_len {data_bak[(i + k) % n_len] = arr[i];}arr.copy_from_slice(&data_bak);
}fn print_array(arr: &[i32]) {for &item in arr {print!("{} ", item);}println!();
}fn main() {let mut data = vec![1, 2, 3, 4, 5, 6, 7];rotate_array(&mut data, 3);print_array(&data);
}实际上,解决旋转数组的问题还可以通过三次反转数组来实现。第一次整体反转,使原数组后k个元素位于前k个元素中,但内部顺序正好相反。第二次反转,只需要反转前k个元素。第三次反转,只需要反转后n-k个元素。需要注意的是:如果k大于数组的长度,需要对k取模,以保证不会超出数组的范围。
接下来,我们来看看如何反转数组。反转数组指的是将数组的顺序颠倒,比如:给定数组为[1, 2, 3, 4, 5, 6, 7],则反转后的数组为[7, 6, 5, 4, 3, 2, 1]。可以通过双指针法来实现反转,先交换数组的第一个数和最后一个数,然后交换第二个数和倒数第二个数,一直到数组中间即可。该方法的时间复杂度为O(n),空间复杂度也为O(1)。具体实现,可参考下面的示例代码。这里,我们通过三次反转数组的部分来完成整个数组的旋转。我们还使用了Rust的swap方法来交换数组中的元素,并且利用了数组的可变引用&mut [i32]来直接修改原数组内容。
fn reverse_array(arr: &mut [i32], mut start: usize, mut end: usize) {while start < end {arr.swap(start, end);start += 1;end -= 1;}
}fn rotate_array(arr: &mut [i32], k: usize) {let n_len = arr.len();let actual_k = k % n_len;reverse_array(arr, 0, n_len - 1);reverse_array(arr, 0, actual_k - 1);reverse_array(arr, actual_k, n_len - 1);
}fn print_array(arr: &[i32]) {for &item in arr {print!("{} ", item);}println!();
}fn main() {let mut data = [1, 2, 3, 4, 5, 6, 7];rotate_array(&mut data, 3);print_array(&data);
}总结
一个问题的解决方案可能远不止一种,正所谓“条条大路通罗马”,如何在众多解决方案中找出最优解,实际上非常考验软件开发工程师的综合能力。从多个角度、多个维度分析和思考问题,是一种非常有效的思维方式,可以帮助我们更全面地理解问题,并找到更好更优的解决方案。
相关文章:

Rust面试宝典第14题:旋转数组
题目 给定一个数组,将数组中的元素向右移动k个位置,其中k是非负数。要求如下: (1)尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。 (2)使用时间复杂度为O(n)和空间…...
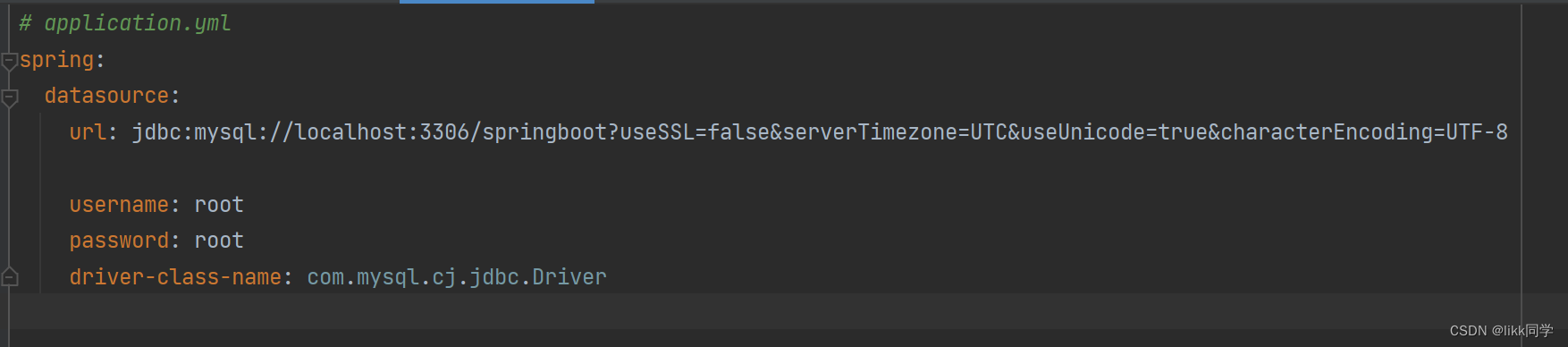
解决SpringBoot中插入汉字变成?(一秒解决)
在这里url后面加一行配置即可&useUnicodetrue&characterEncodingUTF-8即可 解释 spring.datasource.url: 这里包含了数据库的URL,以及额外的参数如useUnicodetrue用于启用Unicode字符集支持,characterEncodingUTF-8用于指定字符编码为UTF-8&…...

5.26牛客循环结构
1002. 难点: 两层循环条件设置 思路 可以设置三个变量 代码 1003 思路: 与星号双塔差不多,在此基础上加大一点难度 每日练题5.23 (EOF用法)-CSDN博客 代码 1004 代码...

AIGC 004-T2I-adapter另外一种支持多条件组合控制的文生图方案!
AIGC 004-T2I-adapter另外一种支持多条件组合控制的文生图方案! 文章目录 0 论文工作1 论文方法2 效果 0 论文工作 T2I-Adapter 论文提出了一种名为 T2I-Adapter 的轻量级适配器模块,旨在增强文本到图像 (T2I) 扩散模型的语义理解和生成能力。 论文指出…...
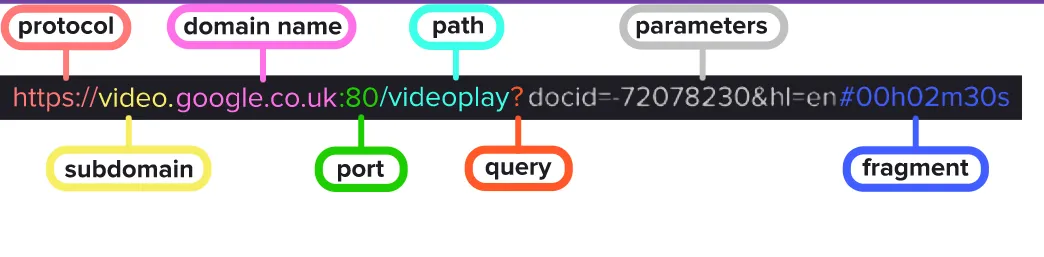
详解 Cookies 和 WebStorage
Cookies 和 WebStorage Cookies 和 WebStorageCookies简要介绍操作 Cookies(document.cookie)不足之处 WebStorage简要介绍LocalStorage Vs. SessionStorage操作 WebStorage 三种数据存储方式的对比分析共性差异 REFERENCES Cookies 和 WebStorage Cook…...

BeanFactory、FactroyBean、ApplicationContext
BeanFactory Ioc容器、定义接口规范来管理spring bean的生命周期、依赖、注入,spring中有各种Ioc容器 FactroyBean 定制的工厂Bean,可以通过抽象工厂方式创建的bean,不纳入spring的生命周期、依赖、注入特性,相当于spring给第三…...

【计算机网络】HTTPS 协议原理
加密 1. 加密概念 加密就是把明文 (要传输的信息)进行一系列变换,生成密文。 解密就是把密文再进行一系列变换,还原成明文。 在这个加密和解密的过程中,往往需要⼀个或者多个中间的数据,辅助进行这个过程,这样的数…...
)
springboot + Vue前后端项目(第十二记)
项目实战第十二记 1.写在前面2. 整合Echarts2.1 vue安装Echarts2.2 使用Echarts2.3 EchartsController编写2.4 Home.vue编写 总结写在最后 1.写在前面 本篇主要讲解系统整合Echarts 2. 整合Echarts 2.1 vue安装Echarts npm i echarts -S2.2 使用Echarts vue中使用echarts的…...

linux 常用命令:find grep ps netstat sudo df du rm
rm 命令 删除 -r 是递归参数(recursive),用于删除目录及其内容。如果不加这个参数,rm 命令无法删除非空目录。-f 是强制参数(force),用于强制删除文件或目录,不会进行任何确认提示…...

SQLiteOpenHelper数据库帮助器
SQLiteOpenHelper数据库帮助器是Android提供的数据库辅助工具。 1、继承SQLiteOpenHelper类,需要重写onCreate和onUpgrade两个方法 案例:实现增删改查 package com.example.databases_text;import android.app.PictureInPictureParams; import androi…...

2024年5月26日 (周日) 叶子游戏新闻
资深开发者:3A游戏当前处于一种尴尬的中间地带游戏行业整体,尤其是3A游戏正处于艰难时期。尽管2023年3A游戏佳作频出,广受好评,但居高不下的游戏开发成本(传闻《漫威蜘蛛侠2》的制作成本高达3亿美元)正严重…...

STM32-10-定时器
STM32-01-认识单片机 STM32-02-基础知识 STM32-03-HAL库 STM32-04-时钟树 STM32-05-SYSTEM文件夹 STM32-06-GPIO STM32-07-外部中断 STM32-08-串口 STM32-09-IWDG和WWDG 文章目录 一、STM32 基础定时器1. 基本定时器简介2. 基本定时器框图3. 基本定时器相关寄存器4. 定时器溢出…...

今天说的什么好呢
先这样吧...
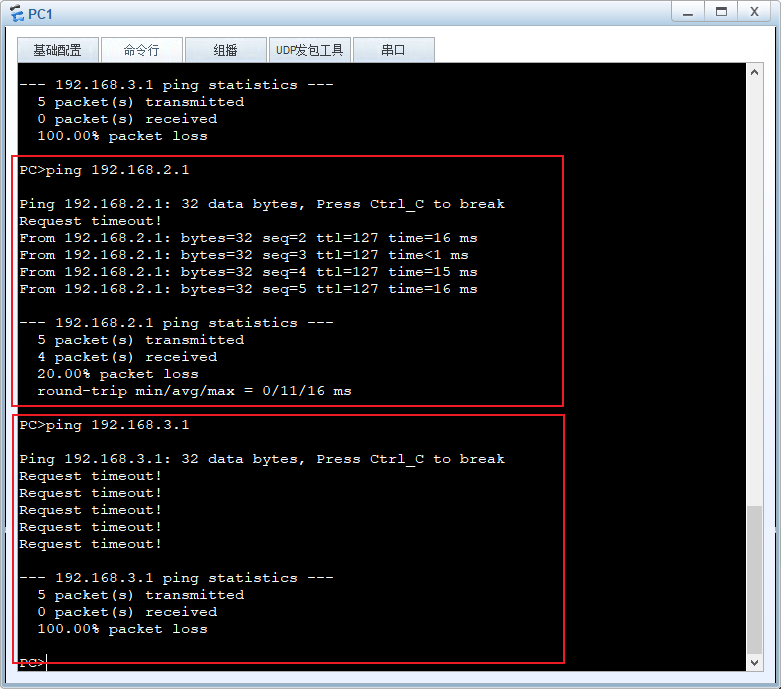
计算机网络-Traffic-Filter流量过滤策略
一、概述 为提高网络安全性,管理人员需要控制进入网络的流量,将不信任的报文丢弃在网络边界。所谓的不信任报文是指对用户来说存在安全隐患或者不愿意接收的报文。同时保证数据访问安全性,企业网络中经常会要求一些部门之间不能相互访问。 背…...
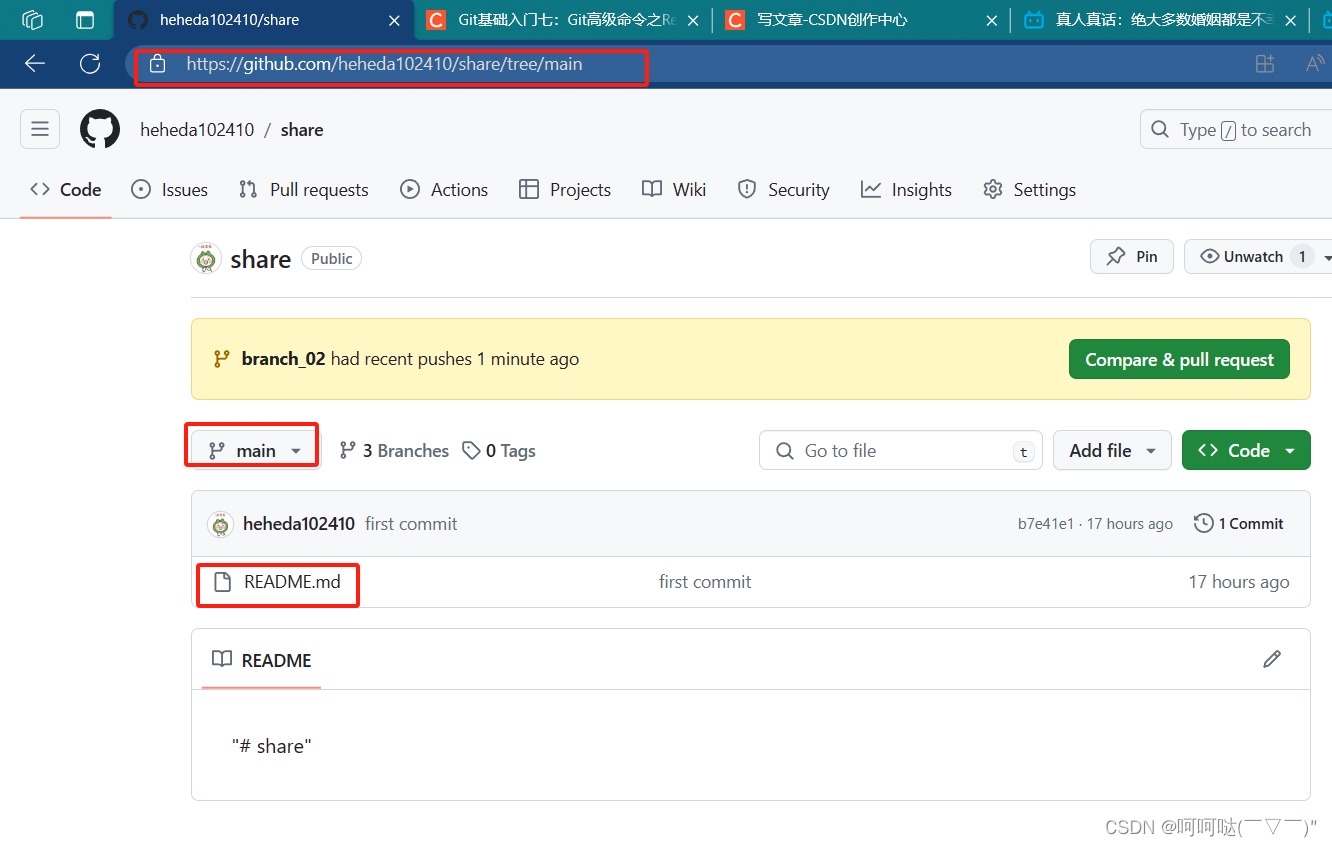
小白入职 必要熟悉 Git / tortoiseGit 工具
1.安装Git 1.1 了解Git Git是分布式版本控制系统,没有中央服务器的每个人的电脑就是一个完整的版本库,工作时无需联网可多人协作,只需把各自的修改推送给对方,就可以互相看到对方的修改了 分布式版本控制工具管理方式ÿ…...
春秋CVE-2022-23906
简介 CMS Made Simple v2.2.15 被发现包含通过上传图片功能的远程命令执行 (RCE) 漏洞。此漏洞通过精心制作的图像文件被利用。 正文 1.进入靶场2.进入登录界面,弱口令admin/123456 3.进入后台,文件上传点 4.上传一句话木马图片 5.复制图片…...

JavaFX安装与使用
前言 最近学习了javafx,开始时在配置环境和导包时遇到了一些麻烦,关于网上很多方法都尝试过了,现在问题都解决了,和大家分享一下我是怎么实现javafx的配置,希望大家可以通过这个方法实现自己的环境配置! 🙈个人主页: 心.c 🔥文章专题:javafx Ὁ…...

漫画|基于SprinBoot+vue的漫画网站(源码+数据库+文档)
漫画网站 目录 基于SprinBootvue的漫画网站 一、前言 二、系统设计 三、系统功能设计 1系统功能模块 2管理员功能模块 3用户功能模块 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: 博主介绍:✌️大…...

python-项目实战
项目实战 1.外星人入侵小游戏 2.数据可视化 3.web应用开发 一、外星人入侵小游戏 需求: 开发大型项目时,做好规划后再动手编写项目很重要。规划可确保你不偏离轨道,从而提高项目成功的可能性。 在游戏《外星人入侵》中,玩家控制着一艘最…...
—— 认识单片机(C51编程))
单片机原理及技术(一)—— 认识单片机(C51编程)
目录 一、单片机概述 1.1 什么是单片机 1.2 单片机的发展历史 1.3 单片机的特点 1.4 MCS-51 系列与 AT89S5x 系列单片机 1.4.1 MCS-51 系列单片机 1.4.2 AT89S5x 系列单片机 1.5 各种衍生品种的8051单片机 1.5.1 STC 系列单片机 1.5.2 C8051Fxxx 系列单片机 一、单片…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
