力扣 第 399 场周赛 解题报告 | 珂学家 | 调和级数 + 分块DP
前言
T1. 优质数对的总数 I
题型: 签到
class Solution:def numberOfPairs(self, nums1: List[int], nums2: List[int], k: int) -> int:res = 0for v1 in nums1:for v2 in nums2:if v1 % (v2 * k) == 0:res += 1return res
T2. 压缩字符串 III
思路: 模拟
感觉引入一个栈,操作更加的方便
当然加限制的分组循环也可以
class Solution:def compressedString(self, word: str) -> str:stk = []for i, c in enumerate(word):if len(stk) == 0 or stk[-1][0] != c or stk[-1][1] == 9:stk.append([c, 1])else:stk[-1][1] += 1return ''.join(map(lambda x: str(x[1]) + x[0], stk))
T3. 优质数对的总数 II
思路: 调和级数
很典的结论题,时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
∑ i = 1 i = n 1 / i = l o g ( n ) \sum_{i=1}^{i=n} 1/i = log(n) i=1∑i=n1/i=log(n)
class Solution:def numberOfPairs(self, nums1: List[int], nums2: List[int], k: int) -> int: mp1 = Counter()for v in nums1:if v % k == 0:mp1[v//k] += 1if len(mp1) == 0:return 0mz = max(mp1.keys())res = 0mp2 = Counter(nums2)for (k1, v1) in mp2.items():for i in range(1, mz // k1 + 1):res += v1 * mp1[i * k1]return res
T4. 不包含相邻元素的子序列的最大和
思路: 分块 + DP
因为数据规模不大, O ( n ∗ q ) O(\sqrt{n} * q) O(n∗q) 在合理的范围内
所以用分块,思路更加的纯朴和简洁。
每次更新块大小内的状态
然后按块间重算最后的整体解
DP 引入块状态, 表示首尾的0-1状态
具体来讲

class Solution {static long inf = Long.MIN_VALUE / 10;static class Block {int l, r;int[] arr;long[][][] pre;int n;public Block(int l, int r, int[] arr) {this.l = l;this.r = r;this.arr = arr;this.n = r - l + 1;pre = new long[n][2][2];}public void modify() {pre[0][0][0] = 0;pre[0][0][1] = inf;pre[0][1][0] = inf;pre[0][1][1] = arr[l];for (int i = 1; i < n; i++) {pre[i][0][0] = Math.max(pre[i - 1][0][0], pre[i - 1][0][1]);pre[i][1][0] = Math.max(pre[i - 1][1][0], pre[i - 1][1][1]);pre[i][0][1] = pre[i - 1][0][0] + arr[l + i];pre[i][1][1] = pre[i - 1][1][0] + arr[l + i];}}long[][] val() {return pre[n - 1];}}public int maximumSumSubsequence(int[] nums, int[][] queries) {int n = nums.length;int z = (int)Math.sqrt(n);int m = (n + z - 1) / z;Block[] blocks = new Block[m];for (int i = 0; i < m; i++) {blocks[i] = new Block(i * z, Math.min((i + 1) * z - 1, n - 1), nums);blocks[i].modify();}long mod = (long)1e9 + 7;long res = 0;for (int i = 0; i < queries.length; i++) {int[] q = queries[i];int p = q[0], x = q[1];int idx = p / z;nums[p] = x;blocks[idx].modify();long[][] dp = new long[m][2];dp[0][0] = Math.max(blocks[0].val()[0][0], blocks[0].val()[1][0]);dp[0][1] = Math.max(blocks[0].val()[0][1], blocks[0].val()[1][1]);for (int j = 1; j < m; j++) {long[][] next = blocks[j].val();dp[j][0] = Math.max(dp[j - 1][0] + Math.max(next[0][0], next[1][0]), dp[j - 1][1] + next[0][0]);dp[j][1] = Math.max(dp[j - 1][0] + Math.max(next[0][1], next[1][1]), dp[j - 1][1] + next[0][1]);}long tmp = Math.max(dp[m - 1][0], dp[m - 1][1]);res = (res + tmp) % mod;res = (res % mod + mod) % mod;}return (int)res;}
}
写在最后

相关文章:

力扣 第 399 场周赛 解题报告 | 珂学家 | 调和级数 + 分块DP
前言 T1. 优质数对的总数 I 题型: 签到 class Solution:def numberOfPairs(self, nums1: List[int], nums2: List[int], k: int) -> int:res 0for v1 in nums1:for v2 in nums2:if v1 % (v2 * k) 0:res 1return resT2. 压缩字符串 III 思路: 模拟 感觉引入一个栈&…...
Redis的下载、安装、启动和初尝试【超级简单】
redis最好是在Linux系统中使用,这是最接近生产实际的环境。 不过,我们初学者,目的是学习Redis的使用、原理,如果在Linux下直接学习Redis,很可能会因为命令不熟悉而劝退,这是不好的。 因此,我主张…...
v-cloak 用于在 Vue 实例渲染完成之前隐藏绑定的元素
如果你是后端开发者(php),在接触一些vue2开发的后台时,会发现有这段代码: # CDN <script src"https://cdn.jsdelivr.net/npm/vue2/dist/vue.js"></script> # 或 <script src"https://cd…...

港股:并不意外的获利了结
中金公司表示,风险偏好驱动的反弹已经较为充分,分歧和获利了结也不意外。接下来或在当前水平震荡盘整,等待更多催化剂。 在持续一个月的大涨后,港股市场上周出现明显回调。此前我们多次提示,市场已经超买,情…...
)
Python项目开发实战:工厂库存管理系统(案例教程)
一、项目背景与意义 随着制造业的快速发展,工厂库存管理成为了企业运营中不可或缺的一部分。一个高效的库存管理系统能够确保物料供应的及时性、降低库存成本、提高生产效率。因此,我们决定使用Python开发一个工厂库存管理系统,以满足工厂日常库存管理的需求。 二、系统需求…...

VS2022 嘿嘿
还是大二的时候就开始用这个,但居然是为了用PB,-_-|| 用了段时间换成了C#,依稀还记得大佬们纠正我的读法,别读C井,应该读C夏普。。。 安装过程其实也没啥,就是关键Key得花时间找,我好不容易搞…...

Flutter 中的 PhysicalShape 小部件:全面指南
Flutter 中的 PhysicalShape 小部件:全面指南 在Flutter中,PhysicalShape小部件是一个能够为子组件添加物理效果的边框和阴影的装饰性小部件。它能够模拟真实世界中物体的立体感,通过在子组件的周围创建一个可自定义的形状,并添加…...

CAD二次开发(6)-用户交互之选择集
1. 简单测试 测试让选中的图形描红 [CommandMethod("SeleDemo")]public void SeleDemo(){Database db HostApplicationServices.WorkingDatabase;Editor ed Application.DocumentManager.MdiActiveDocument.Editor;PromptSelectionResult psr ed.GetSelection();…...

如何使用性能监控工具分析JVM性能瓶颈
1、jConsole: jConsole是JDK自带的Java监控和管理控制台。它提供了一个图形用户界面(GUI),用于监控和管理Java应用程序的性能和资源消耗。 使用方法:打开jdk\bin\jconsole.exe,连接到正在运行的Java进程&a…...
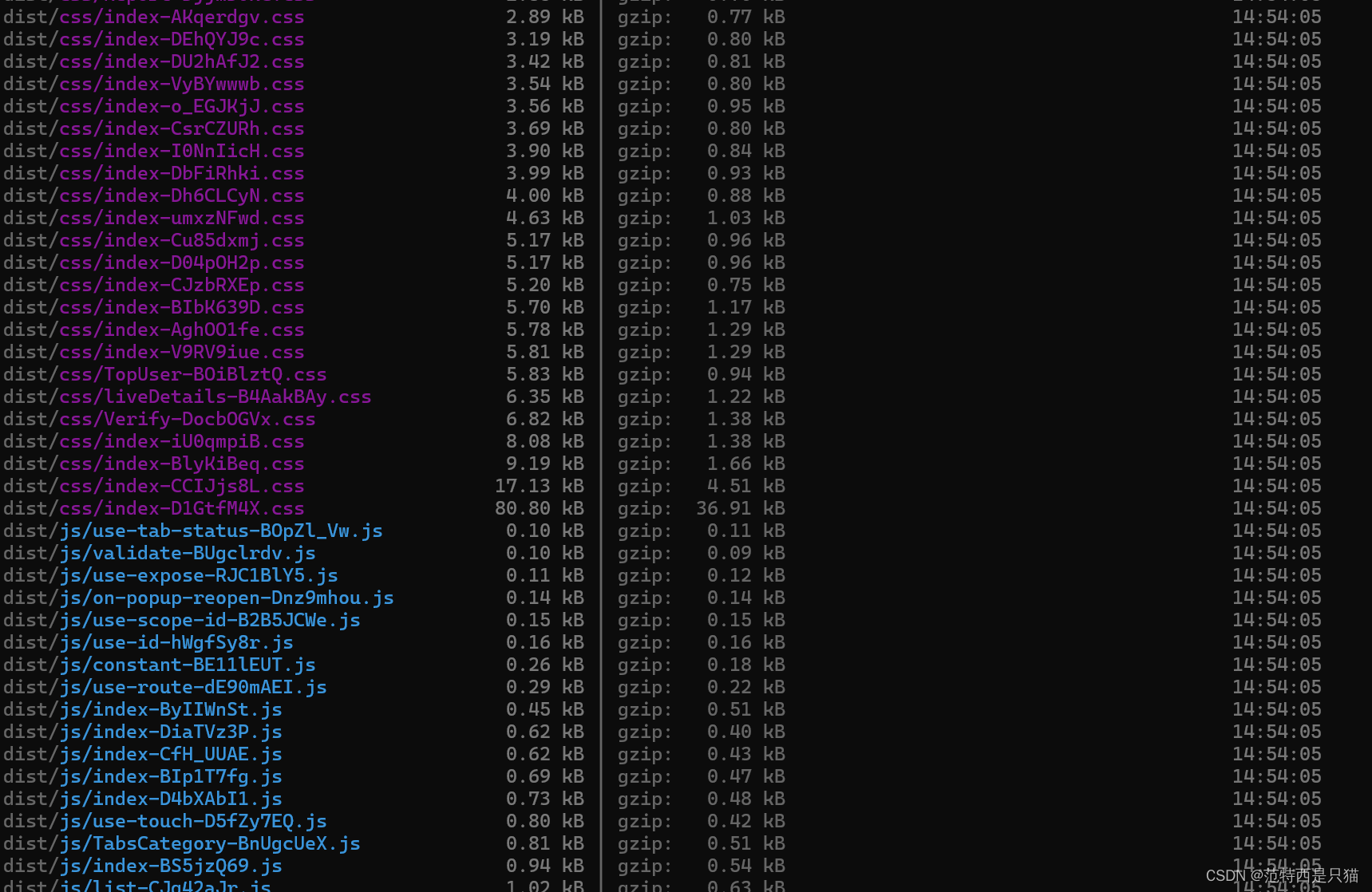
解决vite打包只生成了一个css和js文件问题
文章目录 1. 打包遇到的问题2. 问题原因及修改3. 调整后再次打包🆗 1. 打包遇到的问题 今天整了一个项目,试了下打包,发下打包后只生成了一个css文件,和一个js文件, 这样肯定是不行的,因为这样这个文件的包…...

数据访问层设计_4.灵活运用XML Schema
1.XML Schema XML Schema用来描述XML文档合法结构、内容和限制。XML Schema由XML1.0自描述,并且使用了命名空间,有丰富的内嵌数据类型及其强大的数据结构定义功能,充分地改造了并且极大地扩展了DTDs(传统描述XML文档结构和内容限…...
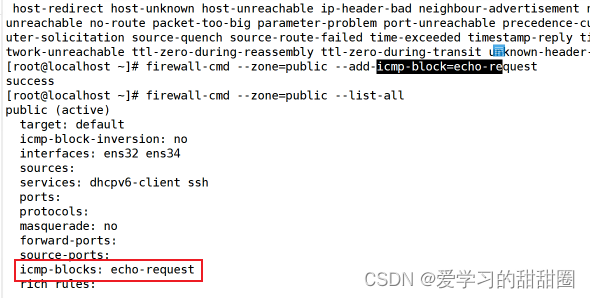
【Linux安全】Firewalld防火墙基础
目录 一、Firewalld概述 二、Firewalld和iptables的关系 三、Firewalld网络区域 1、firewalld防火墙预定义了9个区域: 2、firewalld 数据包处理原则 3、firewalld数据处理流程 4、firewalld检查数据包的源地址的规则 四、Firewalld防火墙的配置方法 1、firewalld 命令…...

先进制造aps专题八 基于ai大模型的ai超级应用,ai生管
目前正在研发的面向消费者的ai超级应用有ai文员,ai教师,ai家教,ai护士,ai翻译 而ai生管无疑是面向制造业的ai超级应用 从商业角度来说,ai生管,必然是aps公司必然要研发的ai超级应用...

Textual for Mac:轻量级IRC客户端
在寻找一款高效、轻量级的IRC客户端时,Textual for Mac无疑是你的不二之选。它集成了众多现代技术,如本机IPv6、最新的IRCv3规范,以及客户端证书身份验证,让你的聊天体验更加顺畅和安全。 Textual for Mac v7.2.2免激活版下载 Tex…...

Facebook:连接世界,畅游社交之旅
作为全球最大的社交平台之一,Facebook不仅仅是一个网站,更是一个连接世界的桥梁,让人们可以轻松地与全球各地的朋友、家人和同事保持联系,分享生活、交流想法,畅游社交的无边界之旅。本文将带领读者探索Facebook的魅力…...

部署PIM-SM
拓扑图 配置 使能组播路由 配置OSPF 组播路由器接口配置pim-sm 连接组成员的接口使能igmp pim路由器上配置静态RP sysname AR1 # multicast routing-enable # interface GigabitEthernet0/0/0ip address 10.1.12.1 255.255.255.0 pim sm # interface GigabitEthernet0/0/…...

一分钟揭秘面试官真实意图,稳拿offer的面试秘诀!
想要在面试中脱颖而出,顺利获得心仪的offer吗?那么,你需要了解面试官背后的潜台词。通过解析这些潜台词,你将能更准确地把握面试官的期望,并给出他们最喜欢的回答。下面,就让我们一起揭开这层神秘的面纱&am…...
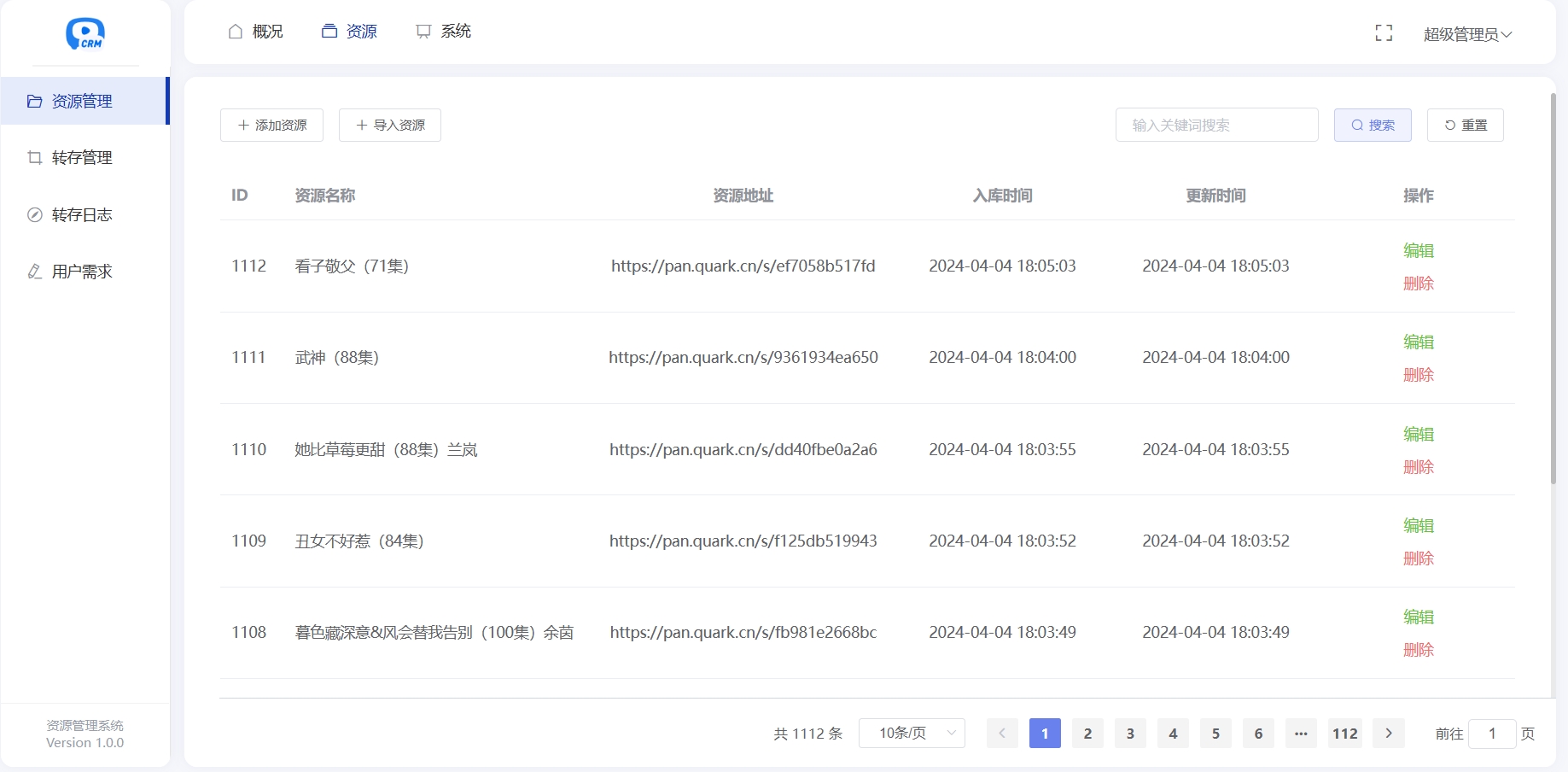
【源码】2024心悦搜剧源码百万级网盘资源
1、一键转存他人链接:就是将别人的分享链接转为你自己的 2、转存心悦搜剧资源:就是将心悦搜剧平台上的所有资源都转成你自己的 3、每日自动更新:自动转存每天的资源并入库 前端uin-app,后端PHP,兼容微信小程序...

燃数科技前端25-40K*14薪一面超简单,下周二面啦
文章末尾扫描二维码领取地址 一面 1、自我介绍 2、低代码如何设计的 3、react路由原理 4、react生命周期 5、什么是回调地狱,如何解决 6、jwt和session有什么区别 7、js文件相互引用有什么问题?如何解决 8、一个很大的json文件…...
读人工智能时代与人类未来笔记14_管控人工智能
1. 管控人工智能 1.1. 历史上的战场进一步推进到与数字网络相连的所有地方 1.2. 数字程序现在控制着一个由众多实体系统构成的庞大且仍在不断增长的领域,而且越来越多的此类系统已实现网络化 1.2.1. 在某些情况下甚至连门锁和冰箱都实现了网络化 1.2.2. 这催生出…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...
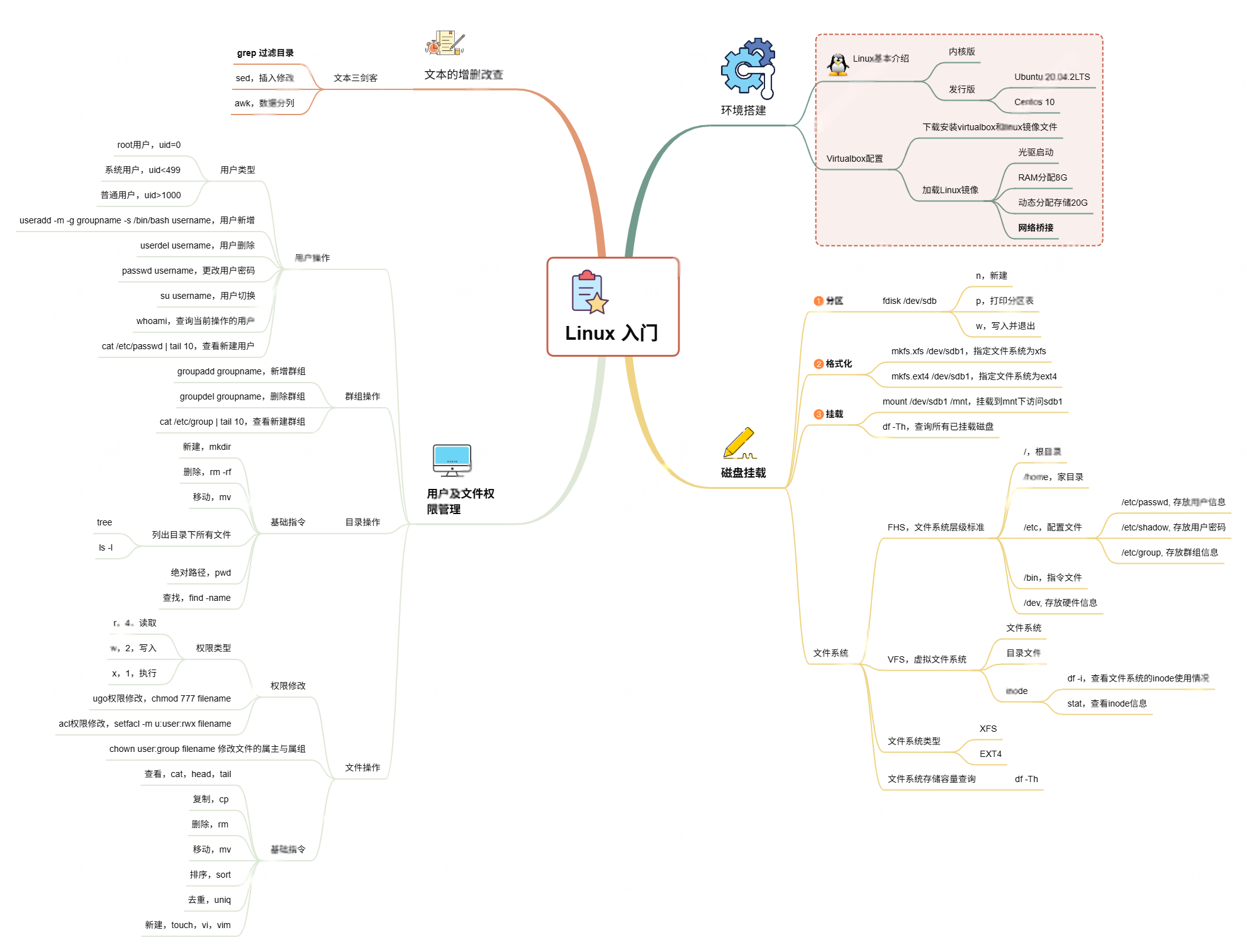
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

