深度学习复盘与小实现
文章目录
- 一、查漏补缺复盘
- 1、python中zip()用法
- 2、Tensor和tensor的区别
- 3、计算图中的迭代取数
- 4、nn.Modlue及nn.Linear 源码理解
- 5、知识杂项思考列表
- 6、KL散度初步理解
- 二、处理多维特征的输入
- 1、逻辑回归模型流程
- 2、Mini-Batch (N samples)
- 三、加载数据集
- 1、Python 魔法方法介绍
- 2、Epoch,Batch-Size,Iteration区别
- 3、加载相关数据集的实现
- 4、在torchvision,datasets数据集
- 四、多分类问题
- 1、softmax 再探究
- 2、独热编码问题
- 五、语言模型初步理解
- 1、语言模型的概念
- 2、语言模型的计算
- 3、 n n n元语法
- 六、相关代码实现
- 1、简易实现小项目代码地址
- 2、简易实现小项目运行过程
- 3、抑郁症数据预处理运行过程
- 4、抑郁症数据训练运行过程
- 七、遇到问题及其解决方案
- 1、pycharm 不能使用GPU加速训练
- 2、google.protobuf.internal冲突问题
一、查漏补缺复盘
1、python中zip()用法
python中zip()用法
应用举例
import numpy as np
import matplotlib.pyplot as pltx_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]def forward(x):return x*wdef loss(x, y):y_pred = forward(x)return (y_pred - y)**2# 穷举法
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):print("w=", w)l_sum = 0for x_val, y_val in zip(x_data, y_data):y_pred_val = forward(x_val)loss_val = loss(x_val, y_val)l_sum += loss_valprint('\t', x_val, y_val, y_pred_val, loss_val)print('MSE=', l_sum/3)w_list.append(w)mse_list.append(l_sum/3)plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
2、Tensor和tensor的区别
首先看下代码区别
>>> a=torch.Tensor([1,2])
>>> a
tensor([1., 2.])
>>> a=torch.tensor([1,2])
>>> a
tensor([1, 2])
- torch.Tensor()是python类,更明确地说,是默认张量类型
torch.FloatTensor()的别名,torch.Tensor([1,2])会调用Tensor类的构造函数__init__,生成单精度浮点类型的张量。 - 而
torch.tensor()仅仅是python函数:https://pytorch.org/docs/stable/torch.html torch.tensor
torch.tensor(data, dtype=None, device=None, requires_grad=False)
- 其中data可以是:list, tuple, NumPy ndarray, scalar和其他类型。
torch.tensor会从data中的数据部分做拷贝(而不是直接引用),根据原始数据类型生成相应的torch.LongTensor、torch.FloatTensor和torch.DoubleTensor。
3、计算图中的迭代取数
注意关注grad取元素规则
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]w = torch.tensor([1.0]) # w的初值为1.0
w.requires_grad = True # 需要计算梯度def forward(x):return x*w # w是一个Tensordef loss(x, y):y_pred = forward(x)return (y_pred - y)**2print("predict (before training)", 4, forward(4).item())for epoch in range(100):for x, y in zip(x_data, y_data):l =loss(x,y) # l是一个张量,tensor主要是在建立计算图 forward, compute the lossl.backward() # backward,compute grad for Tensor whose requires_grad set to Trueprint('\tgrad:', x, y, w.grad.item())w.data = w.data - 0.01 * w.grad.data # 权重更新时,注意grad也是一个tensorw.grad.data.zero_() # after update, remember set the grad to zeroprint('progress:', epoch, l.item()) # 取出loss使用l.item,不要直接使用l(l是tensor会构建计算图)print("predict (after training)", 4, forward(4).item())
.data等于进tensor修改,.item()等于把数拿出来
- w是Tensor(张量类型),Tensor中包含data和grad,data和grad也是Tensor。grad初始为None,调用l.backward()方法后w.grad为Tensor,故更新w.data时需使用w.grad.data。如果w需要计算梯度,那构建的计算图中,跟w相关的tensor都默认需要计算梯度。
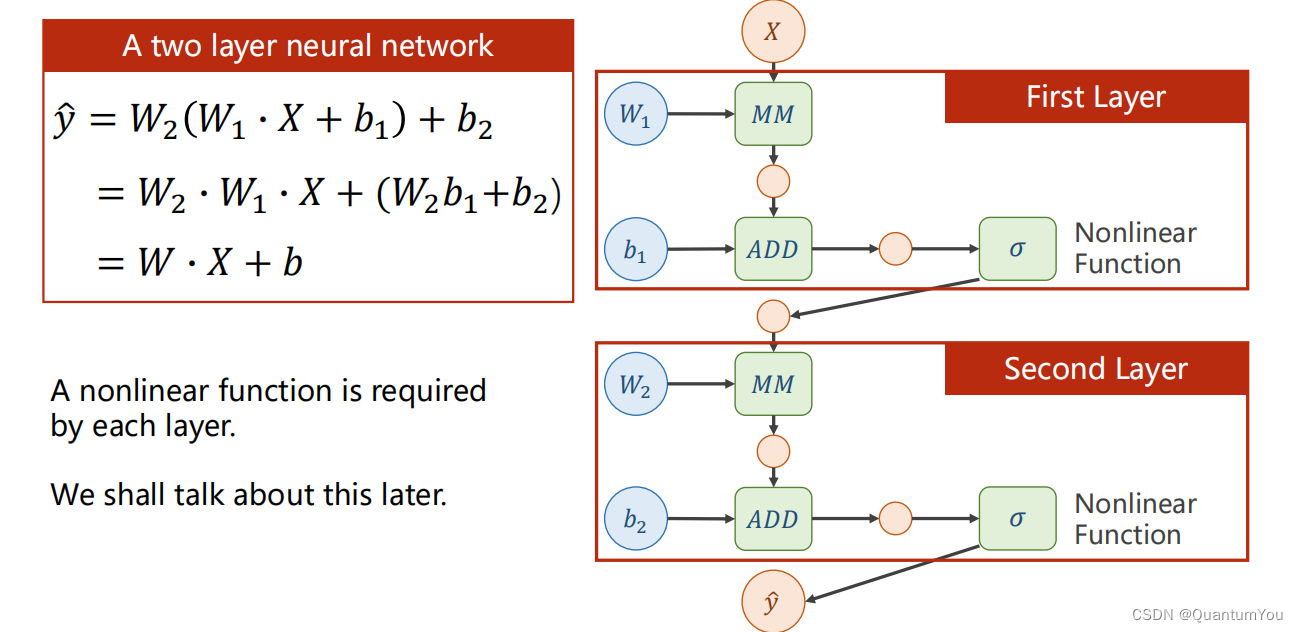
下面的 Linear(1,1 )是input1,output1


4、nn.Modlue及nn.Linear 源码理解
import torch
# prepare dataset
# x,y是矩阵,3行1列 也就是说总共有3个数据,每个数据只有1个特征
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])class LinearModel(torch.nn.Module):def __init__(self):super(LinearModel, self).__init__()# (1,1)是指输入x和输出y的特征维度,这里数据集中的x和y的特征都是1维的# 该线性层需要学习的参数是w和b 获取w/b的方式分别是~linear.weight/linear.biasself.linear = torch.nn.Linear(1, 1)def forward(self, x):y_pred = self.linear(x)return y_predmodel = LinearModel()# construct loss and optimizer
# criterion = torch.nn.MSELoss(size_average = False)
criterion = torch.nn.MSELoss(reduction = 'sum')
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01) # model.parameters()自动完成参数的初始化操作,这个地方我可能理解错了# training cycle forward, backward, update
for epoch in range(100):y_pred = model(x_data) # forward:predictloss = criterion(y_pred, y_data) # forward: lossprint(epoch, loss.item())optimizer.zero_grad() # the grad computer by .backward() will be accumulated. so before backward, remember set the grad to zeroloss.backward() # backward: autograd,自动计算梯度optimizer.step() # update 参数,即更新w和b的值print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())x_test = torch.tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)
参考文章
import torch
from torch import nnm = nn.Linear(20, 30)
input = torch.randn(128, 20)
output = m(input)output.size() # torch.Size([128, 30])- nn.Module 是所有神经网络单元(neural network modules)的基类
pytorch在nn.Module中,实现了__call__方法,而在__call__方法中调用了forward函数。 - 首先创建类对象m,然后通过m(input)实际上调用__call__(input),然后__call__(input)调用
forward()函数,最后返回计算结果为:[ 128 , 20 ] × [ 20 , 30 ] = [ 128 , 30 ]
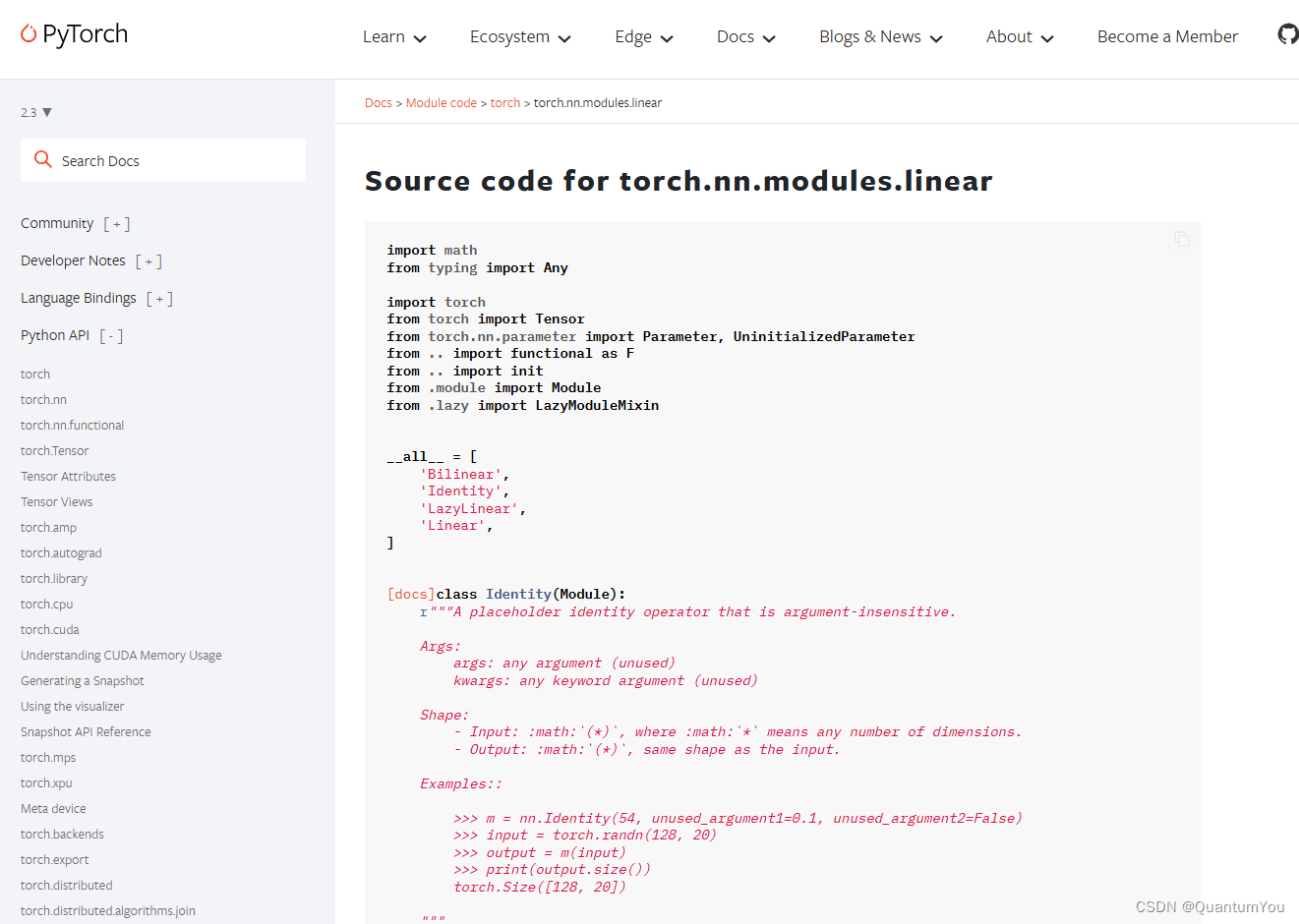
链接
5、知识杂项思考列表
1、SGD单个样本进行梯度下降容易被噪声带来巨大干扰
2、矩阵求导理论书籍 matrix cookbook
3、前向传播是为了计算损失值,反向传播是为了计算梯度来更新模型的参数
6、KL散度初步理解
- KL散度(Kullback-Leibler divergence)是两个概率分布间差异的非对称性度量。参与计算的一个概率分布为真实分布,另一个为理论(拟合)分布,相对熵表示使用理论分布拟合真实分布时产生的信息损耗。
KL散度具有以下几个性质:
- 非负性:KL散度的值始终大于等于0,当且仅当两个概率分布完全相同时,KL散度的值才为0。
- 不对称性:KL散度具有方向性,即P到Q的KL散度与Q到P的KL散度不相等。
- 无限制性:KL散度的值可能为无穷大,即当真实分布中的某个事件在理论分布中的概率为0时,KL散度的值为无穷大。
KL散度的计算公式如下:
D K L ( P ∣ ∣ Q ) = ∑ i P ( i ) log P ( i ) Q ( i ) D_{KL}(P||Q) = \sum_{i}P(i) \log \frac{P(i)}{Q(i)} DKL(P∣∣Q)=i∑P(i)logQ(i)P(i)
其中,(P)和(Q)分别为两个概率分布,(P(i))和(Q(i))分别表示在位置(i)处的概率值。当KL散度等于0时,表示两个概率分布完全相同;当KL散度大于0时,表示两个概率分布存在差异,且值越大差异越大。
- 在机器学习中,KL散度有广泛的应用,例如用于衡量两个概率分布之间的差异,或者用于优化生成式模型的损失函数等。此外,KL散度还可以用于基于KL散度的样本选择来有效训练支持向量机(SVM)等算法,以解决SVM在大型数据集合上效率低下的问题。
逻辑回归构造模板
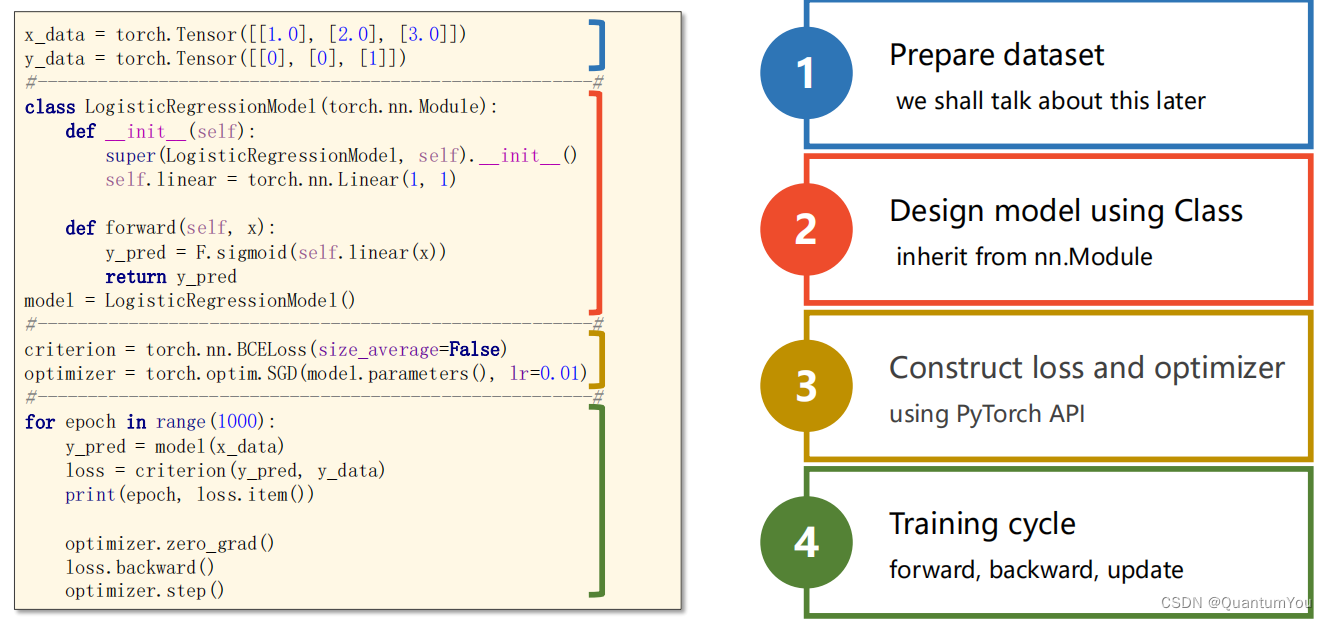
二、处理多维特征的输入
1、逻辑回归模型流程
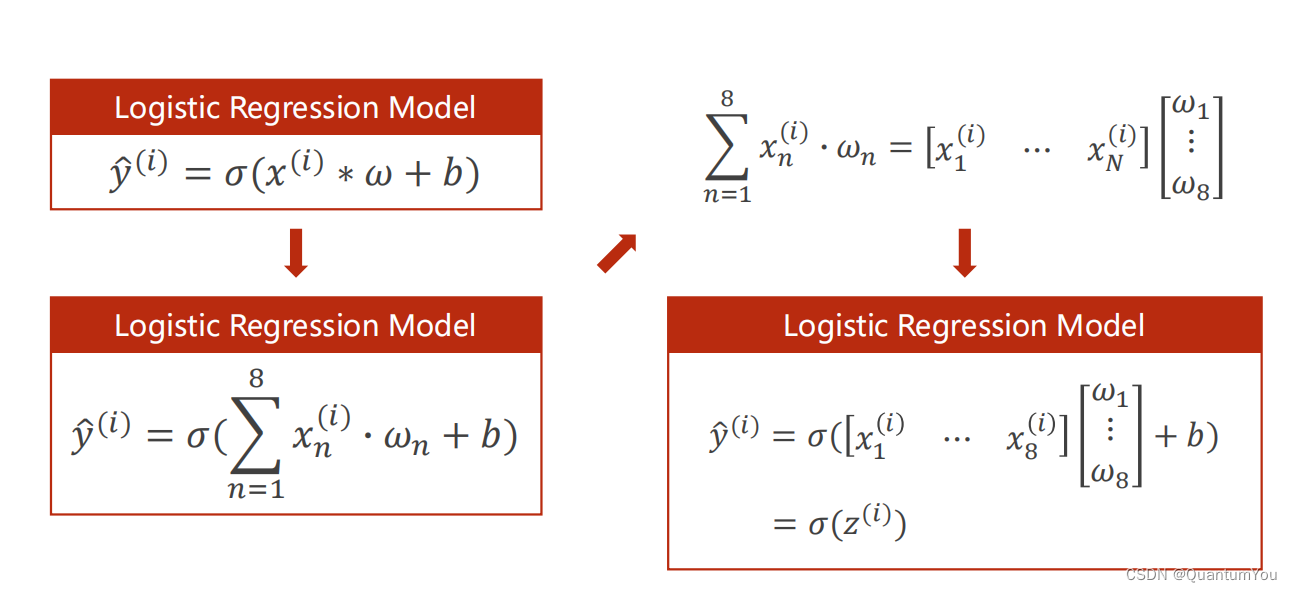
2、Mini-Batch (N samples)
在数学上转化为矩阵运算,转化为向量形式利于GPU进行并行运算

self.linear torch.nn.Linear (8,1)输入为8,输出为1
说明:
-
1、乘的权重(w)都一样,加的偏置(b)也一样。b变成矩阵时使用广播机制。神经网络的参数w和b是网络需要学习的,其他是已知的。
-
2、学习能力越强,有可能会把输入样本中噪声的规律也学到。我们要学习数据本身真实数据的规律,学习能力要有泛化能力。
-
3、该神经网络共3层;第一层是8维到6维的非线性空间变换,第二层是6维到4维的非线性空间变换,第三层是4维到1维的非线性空间变换。

-
4、本算法中
torch.nn.Sigmoid()将其看作是网络的一层,而不是简单的函数使用
torch.sigmoid、torch.nn.Sigmoid和torch.nn.functional.sigmoid的区别
三、加载数据集
- DataLoader 主要加载数据集
说明:
-
1、DataSet 是抽象类,不能实例化对象,主要是用于构造我们的数据集
-
2、DataLoader 需要获取DataSet提供的索引[i]和len;用来帮助我们加载数据,比如说做shuffle(提高数据集的随机性),batch_size,能拿出Mini-Batch进行训练。它帮我们自动完成这些工作。DataLoader可实例化对象。
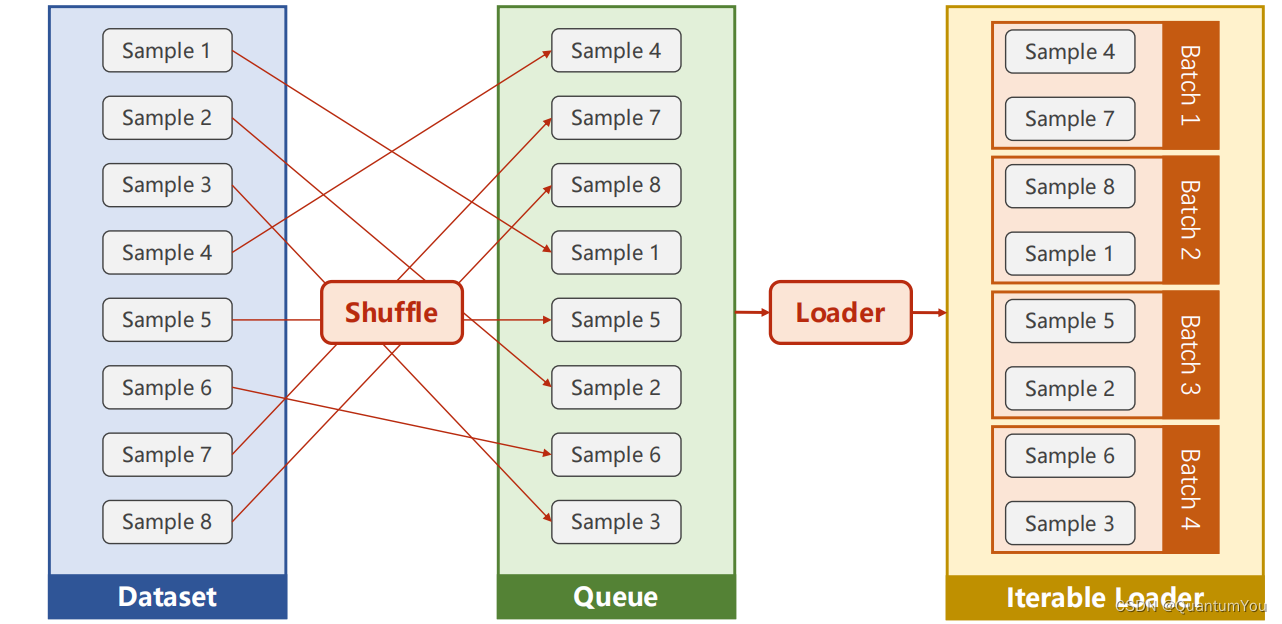
-
3、__getitem__目的是为支持下标(索引)操作
1、Python 魔法方法介绍
- 在Python中,有一些特殊的方法(通常被称为“魔法方法”或“双下划线方法”)是由Python解释器预定义的,它们允许对象进行某些特殊的操作或重载常见的运算符。这些魔法方法通常以双下划线(
__)开始和结束。
- 初始化方法:
__init__(self, ...)
在创建对象时自动调用,用于初始化对象的状态。
class MyClass:def __init__(self, value):self.value = value
- 字符串表示方法:
__str__(self)和__repr__(self)
用于定义对象的字符串表示。__str__用于在print函数中,而__repr__用于在repr函数中。
class MyClass:def __init__(self, value):self.value = valuedef __str__(self):return f"MyClass({self.value})"def __repr__(self):return f"MyClass({self.value})"
- 比较方法:如
__eq__(self, other)、__lt__(self, other)等
用于定义对象之间的比较操作。
class MyClass:def __init__(self, value):self.value = valuedef __eq__(self, other):if isinstance(other, MyClass):return self.value == other.valuereturn False
- 算术运算符方法:如
__add__(self, other)、__sub__(self, other)等
用于定义对象之间的算术运算。
class MyClass:def __init__(self, value):self.value = valuedef __add__(self, other):if isinstance(other, MyClass):return MyClass(self.value + other.value)return NotImplemented
- 容器方法:如
__len__(self)、__getitem__(self, key)、__setitem__(self, key, value)等
-
用于定义对象作为容器(如列表、字典等)时的行为。
-
每个魔法方法是python的内置方法。方法都有对应的内置函数,或者运算符,对这个对象使用这些函数或者运算符时就会调用类中的对应魔法方法,可以理解为重写这些python的内置函数
2、Epoch,Batch-Size,Iteration区别

eg:
10,000 examples --> 1000 Batch-size --> 10 Iteration
1、需要mini_batch 就需要import DataSet和DataLoader
2、继承DataSet的类需要重写init,getitem,len魔法函数。分别是为了加载数据集,获取数据索引,获取数据总量。
3、DataLoader对数据集先打乱(shuffle),然后划分成mini_batch。
4、len函数的返回值 除以 batch_size 的结果就是每一轮epoch中需要迭代的次数。
5、inputs, labels = data中的inputs的shape是[32,8],labels 的shape是[32,1]。也就是说mini_batch在这个地方体现的
在windows 下 wrap 和 linux 下 fork 代码优化

3、加载相关数据集的实现
import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoaderclass DiabetesDataset(Dataset):def __init__(self,filepath):xy = np.loadtxt(filepath,delimiter=',',dtype=np.float32)#shape本身是一个二元组(x,y)对应数据集的行数和列数,这里[0]我们取行数,即样本数self.len = xy.shape[0]self.x_data = torch.from_numpy(xy[:, :-1])self.y_data = torch.from_numpy(xy[:, [-1]])def __getitem__(self, index):return self.x_data[index],self.y_data[index]def __len__(self):return self.len#定义好DiabetesDataset后我们就可以实例化他了
dataset = DiabetesDataset('./data/Diabetes_class.csv.gz')
#我们用DataLoader为数据进行分组,batch_size是一个组中有多少个样本,shuffle表示要不要对样本进行随机排列
#一般来说,训练集我们随机排列,测试集不。num_workers表示我们可以用多少进程并行的运算
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=2)class Model(torch.nn.Module):def __init__(self):#构造函数super(Model,self).__init__()self.linear1 = torch.nn.Linear(8,6)#8维到6维self.linear2 = torch.nn.Linear(6, 4)#6维到4维self.linear3 = torch.nn.Linear(4, 1)#4维到1维self.sigmoid = torch.nn.Sigmoid()#因为他里边也没有权重需要更新,所以要一个就行了,单纯的算个数def forward(self, x):#构建一个计算图,就像上面图片画的那样x = self.sigmoid(self.linear1(x))x = self.sigmoid(self.linear2(x))x = self.sigmoid(self.linear3(x))return xmodel = Model()#实例化模型criterion = torch.nn.BCELoss(size_average=False)
#model.parameters()会扫描module中的所有成员,如果成员中有相应权重,那么都会将结果加到要训练的参数集合上
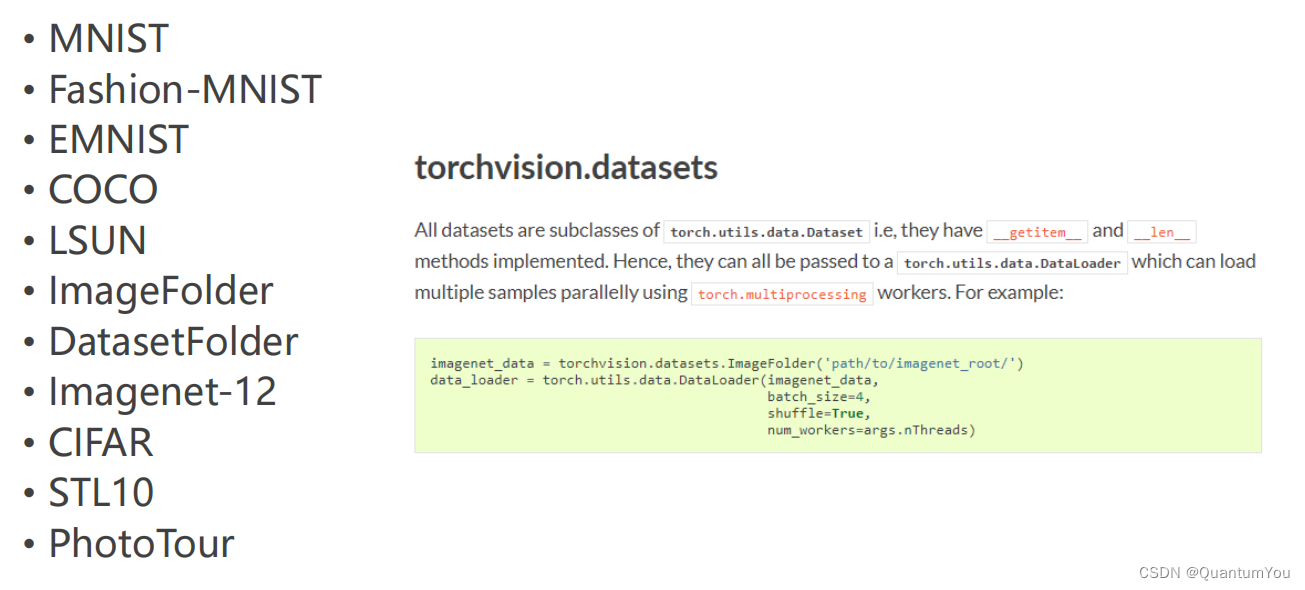
optimizer = torch.optim.SGD(model.parameters(),lr=0.1)#lr为学习率if __name__=='__main__':#if这条语句在windows系统下一定要加,否则会报错for epoch in range(1000):for i,data in enumerate(train_loader,0):#取出一个bath# repare datainputs,labels = data#将输入的数据赋给inputs,结果赋给labels #Forwardy_pred = model(inputs)loss = criterion(y_pred,labels)print(epoch,loss.item())#Backwardoptimizer.zero_grad()loss.backward()#updateoptimizer.step()4、在torchvision,datasets数据集
在torchvision,datasets 下的常见数据集
四、多分类问题
1、softmax 再探究
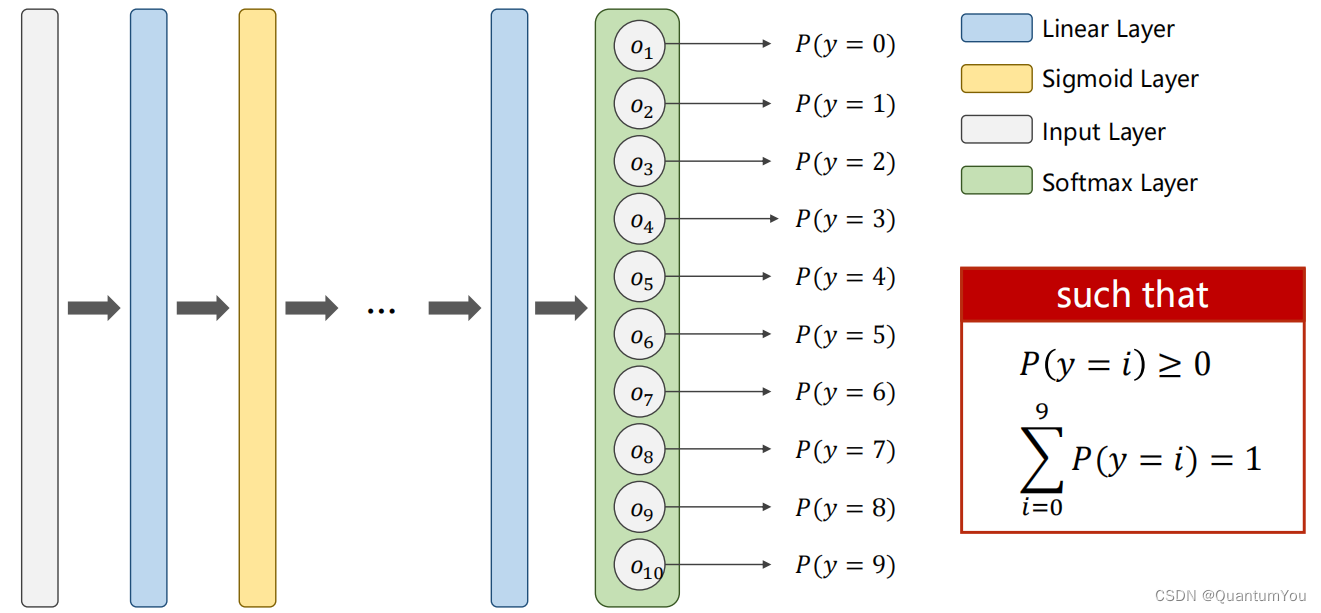
每个类别输出都使用二分类的交叉熵,这样的话所有类别都是一个独立的分布,概率加起来不等于一
注意:我们是将每一个类别看作一个二分类问题,且最后每个输出值需满足两个要求:①≥ 0 ②∑ = 1 即输出的是一个分布。
在神经网络中,特别是在分类任务中,Softmax 函数通常被用作最后一层(线性层或全连接层)的激活函数,以将模型的输出转换为概率分布。对于给定向
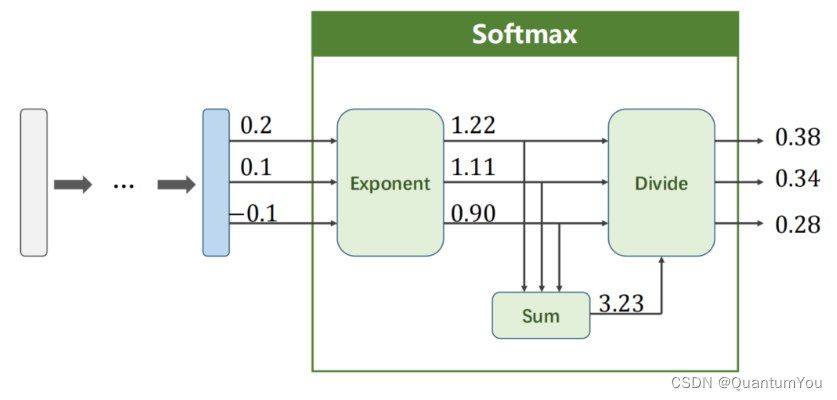
Softmax ( Z l ) i = e Z i l ∑ j = 1 k e Z j l \text{Softmax}(Z^l)_i = \frac{e^{Z^l_i}}{\sum_{j=1}^{k} e^{Z^l_j}} Softmax(Zl)i=∑j=1keZjleZil 对于 i = 0 … … K − 1 \quad \text{对于} \quad i = 0……K-1 对于i=0……K−1
除法是因为归一化
因为输出的是概率,所以要是正数;k个类的概率相互抑制,概率之和是1.所以要先转正再归一化,也就是softmax
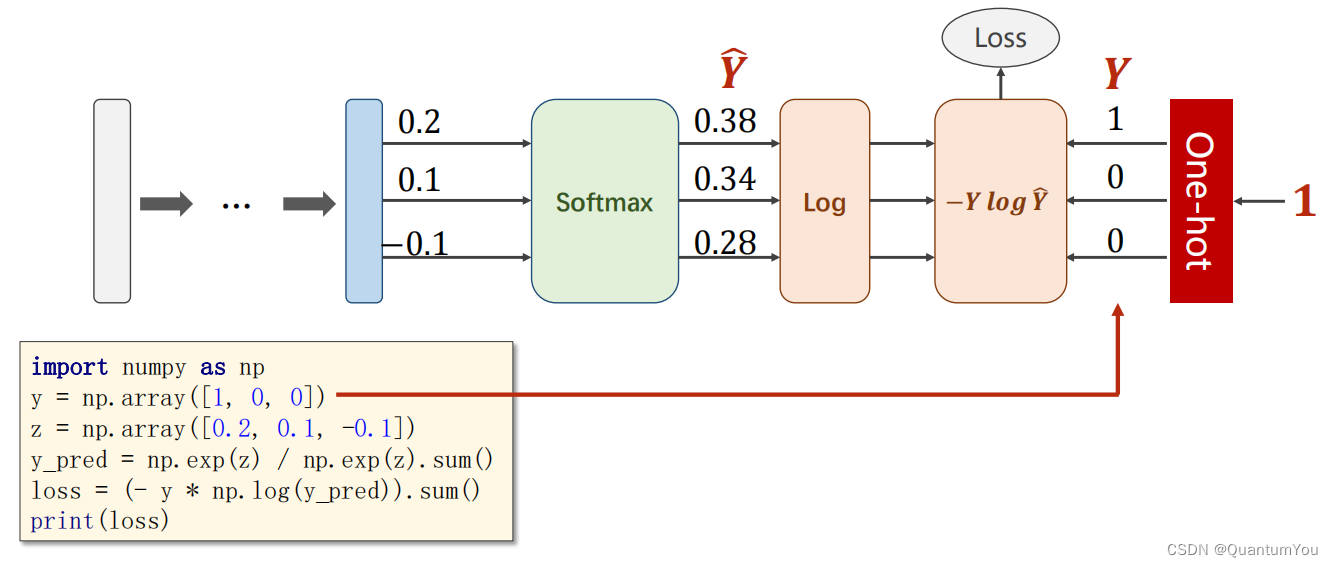
- 在分类任务中,特别是当使用交叉熵损失函数(Cross-Entropy Loss)时,对于给定的预测概率分布 Y ^ \hat{Y} Y^和真实标签 Y,损失函数可以定义为:
Loss ( Y ^ , Y ) = − ∑ i = 1 k Y i log Y ^ i \text{Loss}(\hat{Y}, Y) = -\sum_{i=1}^{k} Y_i \log \hat{Y}_i Loss(Y^,Y)=−i=1∑kYilogY^i
注意这里,(Y) 通常是一个独热编码(one-hot encoded)的向量,其中只有一个元素为1(表示真实的类别),其余元素为0。因此,在实际计算中,由于除了真实类别对应的 (Y_i) 为1外,其余 (Y_i) 都为0,所以求和式中实际上只有一项是有效的。
2、独热编码问题
one-hot介绍
五、语言模型初步理解
1、语言模型的概念
- 语言模型(language model)是自然语言处理的重要技术。自然语言处理中最常见的数据是文本数据。可以把一段自然语言文本看作一段离散的时间序列。假设一段长度为 T T T的文本中的词依次为 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT,那么在离散的时间序列中, w t w_t wt( 1 ≤ t ≤ T 1 \leq t \leq T 1≤t≤T)可看作在时间步(time step) t t t的输出或标签。给定一个长度为 T T T的词的序列 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT,语言模型将计算该序列的概率:
P ( w 1 , w 2 , … , w T ) . P(w_1, w_2, \ldots, w_T). P(w1,w2,…,wT).
2、语言模型的计算
- 假设序列 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT中的每个词是依次生成的,我们有
P ( w 1 , w 2 , … , w T ) = ∏ t = 1 T P ( w t ∣ w 1 , … , w t − 1 ) . P(w_1, w_2, \ldots, w_T) = \prod_{t=1}^T P(w_t \mid w_1, \ldots, w_{t-1}). P(w1,w2,…,wT)=t=1∏TP(wt∣w1,…,wt−1).
例如,一段含有4个词的文本序列的概率
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 1 , w 2 , w 3 ) . P(w_1, w_2, w_3, w_4) = P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3). P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3).
- 为了计算语言模型,我们需要计算词的概率,以及一个词在给定前几个词的情况下的条件概率,即语言模型参数。设训练数据集为一个大型文本语料库,如维基百科的所有条目。词的概率可以通过该词在训练数据集中的相对词频来计算。例如, P ( w 1 ) P(w_1) P(w1)可以计算为 w 1 w_1 w1在训练数据集中的词频(词出现的次数)与训练数据集的总词数之比。因此,根据条件概率定义,一个词在给定前几个词的情况下的条件概率也可以通过训练数据集中的相对词频计算。例如, P ( w 2 ∣ w 1 ) P(w_2 \mid w_1) P(w2∣w1)可以计算为 w 1 , w 2 w_1, w_2 w1,w2两词相邻的频率与 w 1 w_1 w1词频的比值,因为该比值即 P ( w 1 , w 2 ) P(w_1, w_2) P(w1,w2)与 P ( w 1 ) P(w_1) P(w1)之比;而 P ( w 3 ∣ w 1 , w 2 ) P(w_3 \mid w_1, w_2) P(w3∣w1,w2)同理可以计算为 w 1 w_1 w1、 w 2 w_2 w2和 w 3 w_3 w3三词相邻的频率与 w 1 w_1 w1和 w 2 w_2 w2两词相邻的频率的比值。以此类推。
3、 n n n元语法
- 当序列长度增加时,计算和存储多个词共同出现的概率的复杂度会呈指数级增加。 n n n元语法通过马尔可夫假设(虽然并不一定成立)简化了语言模型的计算。这里的马尔可夫假设是指一个词的出现只与前面 n n n个词相关,即 n n n阶马尔可夫链(Markov chain of order n n n)。如果 n = 1 n=1 n=1,那么有 P ( w 3 ∣ w 1 , w 2 ) = P ( w 3 ∣ w 2 ) P(w_3 \mid w_1, w_2) = P(w_3 \mid w_2) P(w3∣w1,w2)=P(w3∣w2)。如果基于 n − 1 n-1 n−1阶马尔可夫链,我们可以将语言模型改写为
P ( w 1 , w 2 , … , w T ) ≈ ∏ t = 1 T P ( w t ∣ w t − ( n − 1 ) , … , w t − 1 ) . P(w_1, w_2, \ldots, w_T) \approx \prod_{t=1}^T P(w_t \mid w_{t-(n-1)}, \ldots, w_{t-1}) . P(w1,w2,…,wT)≈t=1∏TP(wt∣wt−(n−1),…,wt−1).
以上也叫 n n n元语法( n n n-grams)。它是基于 n − 1 n - 1 n−1阶马尔可夫链的概率语言模型。当 n n n分别为1、2和3时,我们将其分别称作一元语法(unigram)、二元语法(bigram)和三元语法(trigram)。例如,长度为4的序列 w 1 , w 2 , w 3 , w 4 w_1, w_2, w_3, w_4 w1,w2,w3,w4在一元语法、二元语法和三元语法中的概率分别为
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ) P ( w 3 ) P ( w 4 ) , P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 2 ) P ( w 4 ∣ w 3 ) , P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 2 , w 3 ) . \begin{aligned} P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2) P(w_3) P(w_4) ,\\ P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3) ,\\ P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_2, w_3) . \end{aligned} P(w1,w2,w3,w4)P(w1,w2,w3,w4)P(w1,w2,w3,w4)=P(w1)P(w2)P(w3)P(w4),=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3),=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w2,w3).
当 n n n较小时, n n n元语法往往并不准确。例如,在一元语法中,由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而,当 n n n较大时, n n n元语法需要计算并存储大量的词频和多词相邻频率。
六、相关代码实现
1、简易实现小项目代码地址
Github
https://github.com/aqlzh/Artificial-intelligence
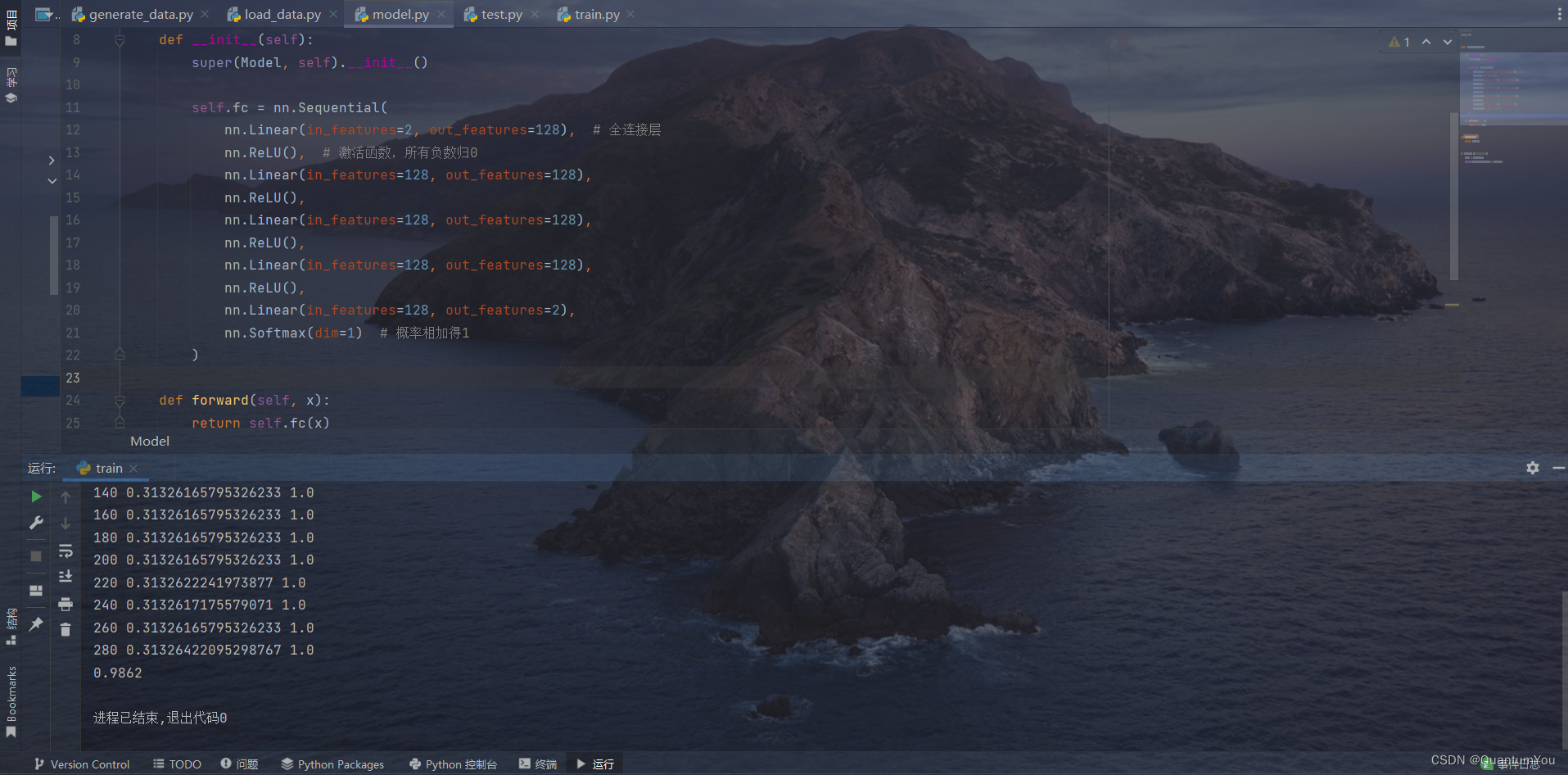
2、简易实现小项目运行过程
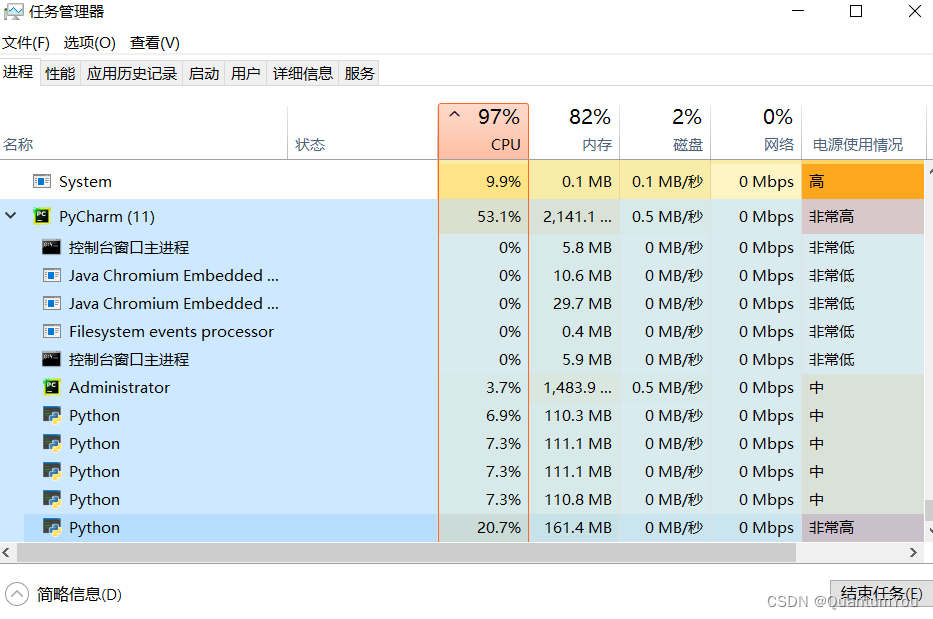
3、抑郁症数据预处理运行过程
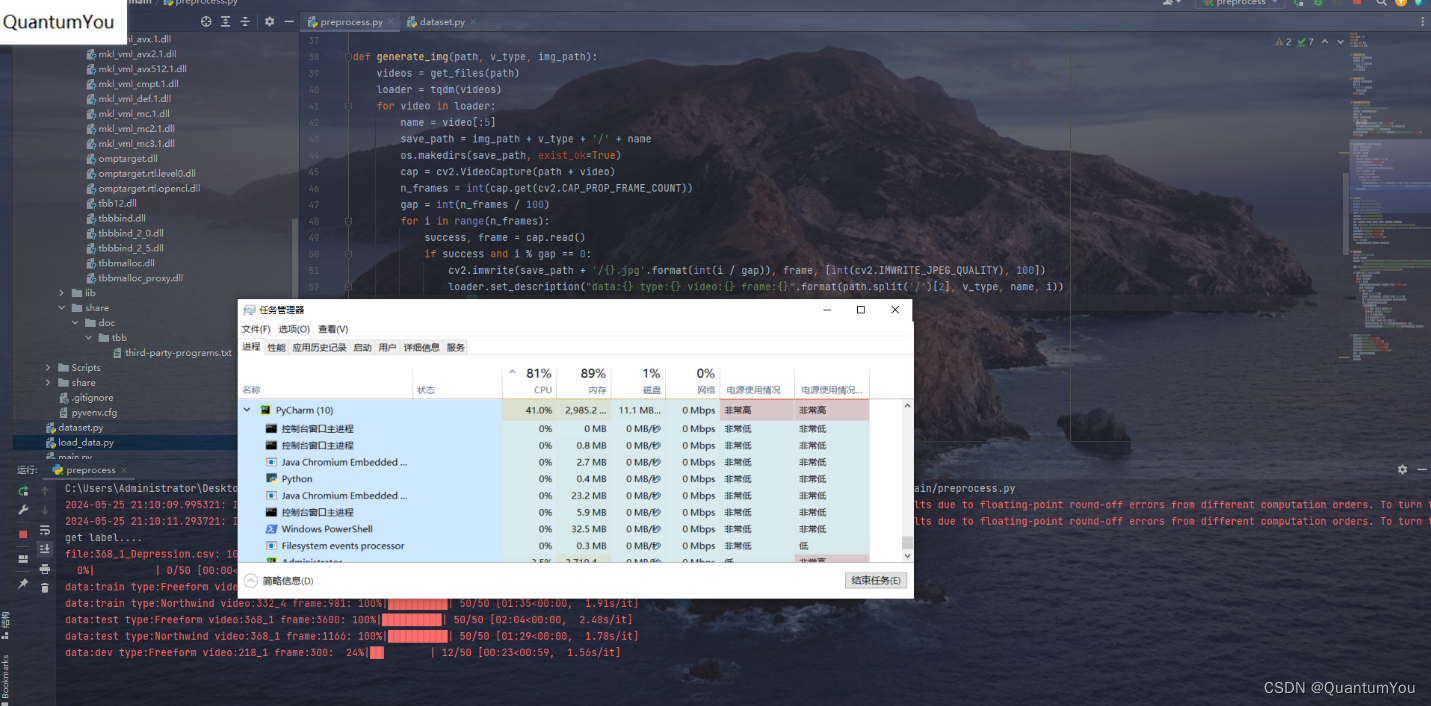
def get_files(path):file_info = os.walk(path)file_list = []for r, d, f in file_info:file_list += freturn file_listdef get_dirs(path):file_info = os.walk(path)dirs = []for d, r, f in file_info:dirs.append(d)return dirs[1:]def generate_label_file():print('get label....')base_url = './AVEC2014/label/DepressionLabels/'file_list = get_files(base_url)labels = []loader = tqdm(file_list)for file in loader:label = pd.read_csv(base_url + file, header=None)labels.append([file[:file.find('_Depression.csv')], label[0][0]])loader.set_description('file:{}'.format(file))pd.DataFrame(labels, columns=['file', 'label']).to_csv('./processed/label.csv', index=False)return labelsdef generate_img(path, v_type, img_path):videos = get_files(path)loader = tqdm(videos)for video in loader:name = video[:5]save_path = img_path + v_type + '/' + nameos.makedirs(save_path, exist_ok=True)cap = cv2.VideoCapture(path + video)n_frames = int(cap.get(cv2.CAP_PROP_FRAME_COUNT))gap = int(n_frames / 100)for i in range(n_frames):success, frame = cap.read()if success and i % gap == 0:cv2.imwrite(save_path + '/{}.jpg'.format(int(i / gap)), frame, [int(cv2.IMWRITE_JPEG_QUALITY), 100])loader.set_description("data:{} type:{} video:{} frame:{}".format(path.split('/')[2], v_type, name, i))cap.release()def get_img():print('get video frames....')train_f = './AVEC2014/train/Freeform/'train_n = './AVEC2014/train/Northwind/'test_f = './AVEC2014/test/Freeform/'test_n = './AVEC2014/test/Northwind/'validate_f = './AVEC2014/dev/Freeform/'validate_n = './AVEC2014/dev/Northwind/'dirs = [train_f, train_n, test_f, test_n, validate_f, validate_n]types = ['Freeform', 'Northwind', 'Freeform', 'Northwind', 'Freeform', 'Northwind']img_path = ['./img/train/', './img/train/', './img/test/', './img/test/', './img/validate/', './img/validate/']os.makedirs('./img/train', exist_ok=True)os.makedirs('./img/test', exist_ok=True)os.makedirs('./img/validate', exist_ok=True)for i in range(6):generate_img(dirs[i], types[i], img_path[i])def get_face():print('get frame faces....')detector = MTCNN()save_path = ['./processed/train/Freeform/', './processed/train/Northwind/', './processed/test/Freeform/','./processed/test/Northwind/', './processed/validate/Freeform/', './processed/validate/Northwind/']paths = ['./img/train/Freeform/', './img/train/Northwind/', './img/test/Freeform/', './img/test/Northwind/','./img/validate/Freeform/', './img/validate/Northwind/']for index, path in enumerate(paths):dirs = get_dirs(path)loader = tqdm(dirs)for d in loader:os.makedirs(save_path[index] + d.split('/')[-1], exist_ok=True)files = get_files(d)for file in files:img_path = d + '/' + files_path = save_path[index] + d.split('/')[-1] + '/' + fileimg = cv2.cvtColor(cv2.imread(img_path), cv2.COLOR_BGR2RGB)info = detector.detect_faces(img)if (len(info) > 0):x, y, width, height = info[0]['box']confidence = info[0]['confidence']b, g, r = cv2.split(img)img = cv2.merge([r, g, b])img = img[y:y + height, x:x + width, :]cv2.imwrite(s_path, img, [int(cv2.IMWRITE_JPEG_QUALITY), 100])loader.set_description('confidence:{:4f} img:{}'.format(confidence, img_path))if __name__ == '__main__':os.makedirs('./img', exist_ok=True)os.makedirs('./processed', exist_ok=True)os.makedirs('./processed/train', exist_ok=True)os.makedirs('./processed/test', exist_ok=True)os.makedirs('./processed/validate', exist_ok=True)label = generate_label_file()get_img()get_face()数据预处理时间最长的一集 😢😢
预处理有两步骤
- 第一步是从视频中提取图片(抽取视频帧,每个视频按间隔抽取100-105帧)
- 第二步是从图片中提取人脸信息(使用MTCNN提取人脸,并分割图片)
预处理数据成功,结果如下(跑了一整个晚上)😵😵
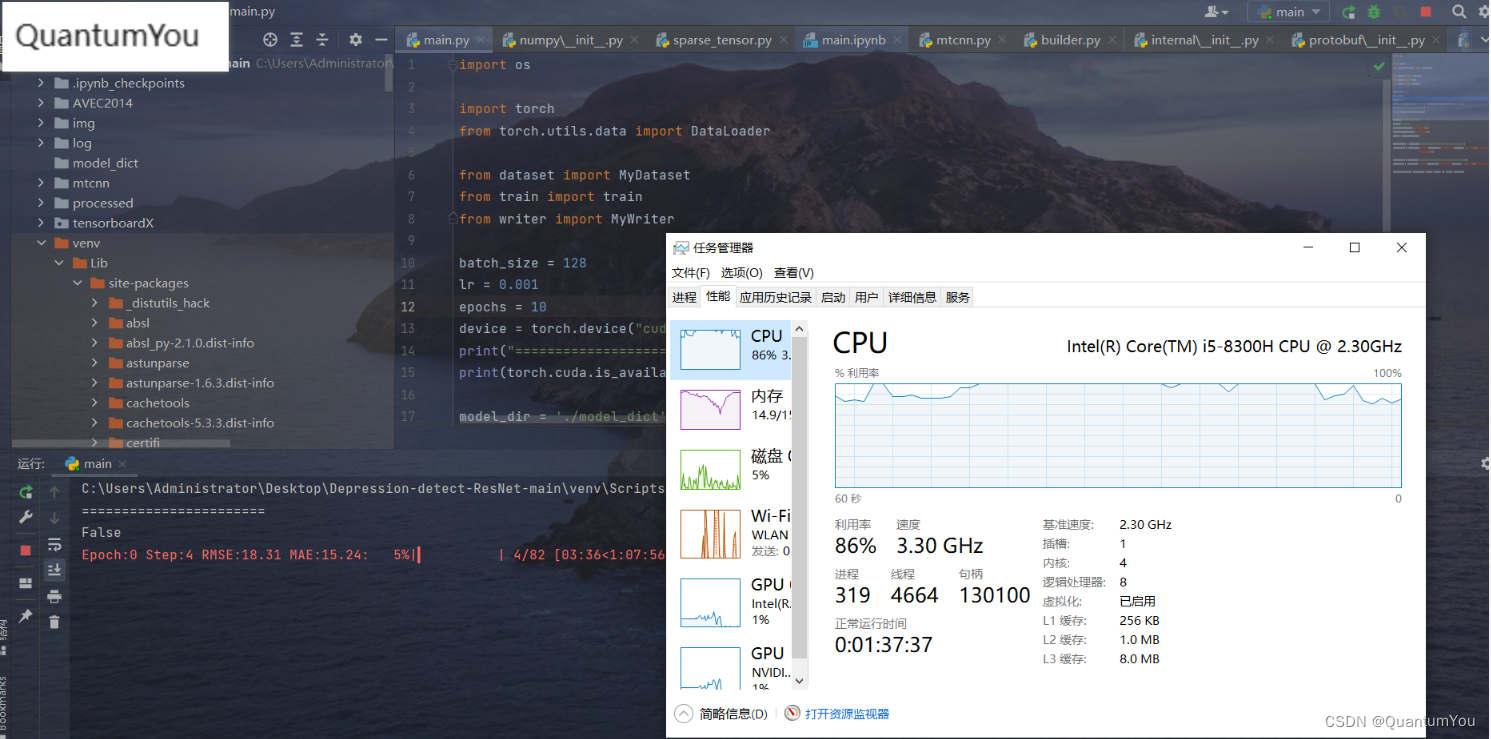
4、抑郁症数据训练运行过程
电脑配置感觉跟不上了,跑不动了,epoch 0 都跑了大半天😱😱
七、遇到问题及其解决方案
1、pycharm 不能使用GPU加速训练
https://blog.csdn.net/QuantumYou/article/details/139215013?spm=1001.2014.3001.5501
2、google.protobuf.internal冲突问题
https://blog.csdn.net/QuantumYou/article/details/139212458?spm=1001.2014.3001.5501

相关文章:

深度学习复盘与小实现
文章目录 一、查漏补缺复盘1、python中zip()用法2、Tensor和tensor的区别3、计算图中的迭代取数4、nn.Modlue及nn.Linear 源码理解5、知识杂项思考列表6、KL散度初步理解 二、处理多维特征的输入1、逻辑回归模型流程2、Mini-Batch (N samples) 三、加载数据集1、Python 魔法方法…...
)
算法刷题笔记 高精度加法(C++实现)
文章目录 题目描述题目思路和代码 题目描述 给定两个正整数(不含前导0),计算它们的和。 输入格式 共两行,每行包含一个整数。 输出格式 共一行,包含所求的和。 题目思路和代码 基本思路:模拟竖式计算…...

php祛除mqtt 返回数据中包含的特殊字符
function cleanseMessage($message) {// 定义特殊字符的正则表达式$pattern /[[:^print:]]/;// 使用正则表达式替换特殊字符为空字符串$cleanedMessage preg_replace($pattern, , $message);return $cleanedMessage; }// 假设接收到的MQTT消息是: $rawMessage &q…...

2024,java开发,已经炸了吗?
网友: 炸的透透的了,坐标南京。 一月底,一个好哥们,双休朝九晚六不加班18K,被裁。 入职不到两年,算是工资和年终奖才赔了6.5W左右。 上周五新公司入职,周六开始加班。现在每周134加班到晚上八…...

c++基础篇
一、命名空间: 1.1命名空间存在的意义: 1.1要知道c是对c语言缺点的完善,而在c语言中我们是知道,定义变量、函数名或者全域名是不能相同的,否则会产生冲突,但要知道这都是大量存在的,就像一个名…...

卫浴行业All in 智能化,国货品牌拿到了先手棋
想要了解一个行业的趋势和风向,展会可以说是最佳的窗口。 比如半个月前在上海举办的第28届中国国际厨房、卫浴设施展览会上,1500多家国内外企业同台竞技,给出了各自的解决方案,其中“智能化”已成为出镜率最高的词汇。 走在数智…...

分享10个国内可以使用的GPT中文网站
在今天的人工智能领域,基于对话的语言模型已成为研究的热点,尤其是像 ChatGPT 这样因其出色的语言理解与对话交互能力而广受关注的模型。本文将介绍10个国内可以直接使用GPT的网站,旨在为大家在选择和使用这些优秀的AI工具时提供有价值的参考…...

golang实现mediasoup的tcp服务及channel通道
tcp模块 定义相关类 Client:表示客户端连接,包含网络连接conn、指向服务器的指针Server和Channel指针c。server:表示TCP服务器,包含服务器地址address、TLS配置config以及三个回调函数: onNewClientCallback…...

Spring:IoC容器(基于注解管理bean)
1. HelloWorld * 引入依赖* 开启组件扫描* 使用注解定义 Bean* 依赖注入 2.开启组件扫描 <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/20…...

如何解决Redis缓存雪崩问题?
解决Redis缓存雪崩问题,可以从多个方面入手来确保系统在高并发和缓存失效时能够保持稳定运行。以下是一些具体的解决策略: 合理设置缓存过期时间: 避免大量缓存设置相同的过期时间,这样会导致在某一时刻缓存同时失效,…...

vue3的组件通信v-model使用
一、组件通信 1.props 》 父向子传值 props 主要用于父组件向子组件通信。再父组件中通过使用:msgmsg绑定需要传给子组件的属性值,然后再在子组件中用props接收该属性值 方法一 普通方式:// 父组件 传值<child :msg1"msg1" :list"list">…...

从关键新闻和最新技术看AI行业发展(2024.5.6-5.19第二十三期) |【WeThinkIn老实人报】
写在前面 【WeThinkIn老实人报】旨在整理&挖掘AI行业的关键新闻和最新技术,同时Rocky会对这些关键信息进行解读,力求让读者们能从容跟随AI科技潮流。也欢迎大家提出宝贵的优化建议,一起交流学习💪 欢迎大家关注Rocky的公众号&…...
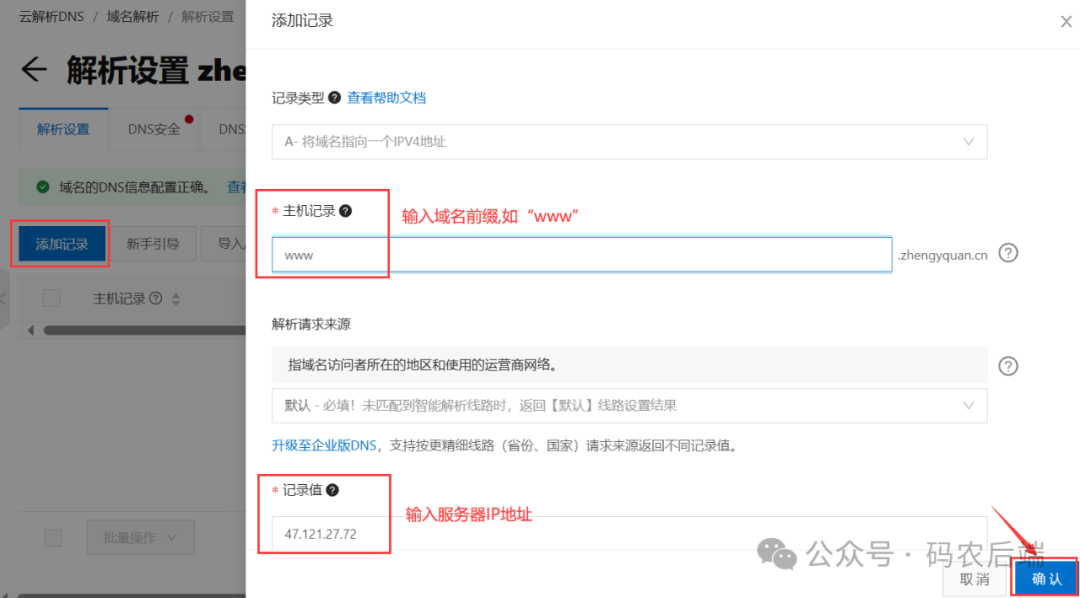
一文带你学会如何部署个人博客到云服务器,并进行域名备案与解析!
哈喽,大家好呀!这里是码农后端。之前我给大家介绍了如何快速注册一个自己的域名,并创建一台自己的阿里云ECS云服务器。本篇将介绍如何将个人博客部署到云服务器,并进行域名备案与解析。 1、域名备案 注册了域名并购买了云服务器之…...

YoloV8实战:复现基于多任务的YoloV8方案
摘要 自动驾驶中多任务学习,特别是通过设计一种自适应、实时且轻量级的模型来同时处理目标检测、可行驶区域分割和车道线分割,是一种非常有用的研究方法,其中最出名的当属YOLOP模型。然后,YoloP在实时性上并没有得到满足,本文复现基于YoloV8的对任务方案,并在BDD100K数据…...

专题汇编 | ChatGPT引领AIGC新浪潮(一)
ChatGPT的产生与迭代 2022年11月末,美国人工智能研究实验室OpenAI推出ChatGPT。上线的ChatGPT只用了2个月,活跃用户数就突破了1亿,创造了应用增速最快的纪录。 ChatGPT是什么 ChatGPT是一种人工智能技术驱动的自然语言处理(Natural Language Processing,NLP)工具,使用的…...
Excel分类汇总,5个做法,提高数据处理效率!
在日常的工作中,我们经常需要使用Excel中的各种功能,Excel分类汇总功能无疑是数据分析和报告制作中的一把利器,它极大地提高了数据处理的效率和准确性。在现代商业环境中,数据无处不在,而如何从这些数据中提取有效信息…...

使用Nginx实现高可用HTTP和TCP代理:健康检查与最佳实践配置20240523
使用Nginx实现高可用HTTP和TCP代理:健康检查与最佳实践配置 在现代分布式系统中,确保应用的高可用性至关重要。Nginx作为一个高性能的HTTP服务器和反向代理,同时也支持TCP代理,通过合理配置可以大大提高系统的可用性。本文将深入…...

代码随想录算法训练营Day52 | 300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组 | Python | 个人记录向
注:Day51休息。 本文目录 300.最长递增子序列做题看文章 674. 最长连续递增序列做题看文章 718. 最长重复子数组做题看文章 以往忽略的知识点小结个人体会 300.最长递增子序列 代码随想录:300.最长递增子序列 Leetcode:300.最长递增子序列 …...

Python编程的黑暗魔法:模块与包的神秘力量!
哈喽,我是阿佑,今天给大家讲讲模块与包~ 文章目录 1. 引言1.1 模块化编程的意义1.2 Python中模块与包的概念概述 2. 背景介绍2.1 Python模块系统模块的定义与作用Python标准库简介 2.2 包的结构与目的包的定义与目录结构包在项目组织中的重要性 3. 创建与…...

python编程不良习惯纠正: 慎用顶层代码
这几天在跑一个开源代码时,发现,通过pdb断点不起作用,经过一番检查,发现代码运行时甚至没有进入main函数,就开始一顿操作. 然后定位到是在执行"import"操作的时候发生了冗余操作. 经过进一步的检查发现,是下…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
