机器学习之词袋模型
目录
1 词袋模型基本概念
2 词袋模型的表示方法
2.1 三大方法
1 独热表示法(One-Hot)
2 词频表示法(Term Frequency, TF)
3 词频-逆文档频率表示法(TF-IDF)
2.2 例子
1 词袋模型基本概念
词袋模型(Bow,Bag of Words)不考虑文本中词与词之间的上下文关系,仅仅只考虑所有词的权重(与词在文本中出现的频率有关),类似于将所有词语装进一个袋子里,其中每个词的出现都是独立的,不依赖于其他词是否出现。这种模型的主要目的是将文本转换为一个向量,其中向量的每个维度代表一个词,而该维度的值则表示该词在文本中出现的频率。
词袋模型的主要特征是:每个词的出现都是独立的,相当于每次随机试验为随机从词表中抽取一个单词,进行n次独立重复试验,因此适合使用多项式朴素贝叶斯
2 词袋模型的表示方法
2.1 三大方法
1 独热表示法(One-Hot)
One-Hot表示法的数值计算规则为:词语序列中出现的词语的数值为1,词语序列中未出现的词语的数值为0。其数学表达式为:
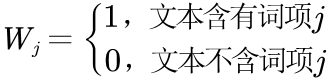
2 词频表示法(Term Frequency, TF)
TF表示法的数值计算规则为:词语序列中出现的词语的数值为该词语在所在文本中的频次,词语序列中未出现的词语的数值为0。其数学表达式为:

其中,表示词语
,
表示词语
在所在文本出现的次数。
3 词频-逆文档频率表示法(TF-IDF)
TF-IDF的核心思想是:
- 如果某个词语在文本中频繁出现,则认为该词语很重要
- 如果某个词语在文本中频繁出现,但该词语在每篇文档都出现,则认为该词语不是特别重要,比如“的”字每篇文章都出现,但是重要性不大
TF-IDF表示法的数值计算规则为:词语序列中出现的词语的数值为词语在所在文本中的频次乘以词语的逆文档频率,词语序列中未出现的词语的数值为0。其数学表达式为:

其中,表示词语
,
表示词语
在所在文本出现的次数。
的计算公式为:

当分母越大,越小,则说明其越不重要,为了防止分母为0,对
进行改进,如下:

2.2 例子
已知有下边的几篇英文文本,请分别用词袋模型的三种方法来向量化表示每篇文本。
| 文档ID | 文档词列表 |
|---|---|
| 1 | Chinese Beijing Chinese |
| 2 | Chinese Chinese Shanghai |
| 3 | Chinese Macao |
| 4 | Tokyo Japan Chinese |
第一步:构建词袋
第二步:对于每一篇文本,计算词袋中各词语的数值,得到该篇文本的向量
One-Hot表示法
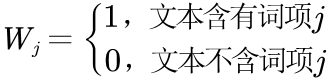
根据上述公式可得:
| Beijing | Chinese | Japan | Macao | Shanghai | Tokyo | |
|---|---|---|---|---|---|---|
| Chinese Beijing Chinese | 1 | 1 | 0 | 0 | 0 | 0 |
| Chinese Chinese Shanghai | 0 | 1 | 0 | 0 | 1 | 0 |
| Chinese Macao | 0 | 1 | 0 | 1 | 0 | 0 |
| Tokyo Japan Chinese | 0 | 1 | 1 | 0 | 0 | 1 |
词频表示法

根据上述公式可得:
| Beijing | Chinese | Japan | Macao | Shanghai | Tokyo | |
|---|---|---|---|---|---|---|
| Chinese Beijing Chinese | 1 | 2 | 0 | 0 | 0 | 0 |
| Chinese Chinese Shanghai | 0 | 2 | 0 | 0 | 1 | 0 |
| Chinese Macao | 0 | 1 | 0 | 1 | 0 | 0 |
| Tokyo Japan Chinese | 0 | 1 | 1 | 0 | 0 | 1 |
TF-IDF表示法

使用改进后的,如下:

计算过程如下:
因此有:
| Beijing | Chinese | Japan | Macao | Shanghai | Tokyo | |
|---|---|---|---|---|---|---|
| Chinese Beijing Chinese | 1*1.916=1.916 | 2*1=2 | 0 | 0 | 0 | 0 |
| Chinese Chinese Shanghai | 0 | 2*1=2 | 0 | 0 | 1*1.916=1.916 | 0 |
| Chinese Macao | 0 | 1*1=1 | 0 | 1*1.916=1.916 | 0 | 0 |
| Tokyo Japan Chinese | 0 | 1*1=1 | 1*1.916=1.916 | 0 | 0 | 1*1.916=1.916 |
相关文章:
机器学习之词袋模型
目录 1 词袋模型基本概念 2 词袋模型的表示方法 2.1 三大方法 1 独热表示法(One-Hot) 2 词频表示法(Term Frequency, TF) 3 词频-逆文档频率表示法(TF-IDF) 2.2 例子 1 词袋模型基本概念 词袋模型&a…...

【C++/STL】vector(常见接口、模拟实现、迭代器失效)
🌈个人主页:秦jh_-CSDN博客🔥 系列专栏: https://blog.csdn.net/qinjh_/category_12575764.html?spm1001.2014.3001.5482 目录 简单使用 常见接口 find insert vector模板 模拟实现 尾插 构造 迭代器失效 使用memcpy拷贝问…...

Spring Boot Web 开发:MyBatis、数据库连接池、环境配置与 Lombok 全面解析
推荐一个AI网站,免费使用豆包AI模型,快去白嫖👉海鲸AI 1.0 MyBatis 概述 MyBatis 是一个优秀的持久层框架,它支持自定义 SQL、存储过程以及高级映射。MyBatis 可以帮助我们将数据库操作抽象出来,使得我们的代码更加简洁…...
【UE5.1 多线程 异步】“Async Blueprints Extension”插件使用记录
目录 一、异步生成Actor示例 二、异步计算示例 参考视频 首先需要在商城中下载“Async Blueprints Extension”插件 一、异步生成Actor示例 2. 创建一个线程类,这里要指定父类为“LongAsyncTask”、“InfiniteAsyncTask”、“ShortAsyncTask”中的一个 在线程类…...

【已解决】在jupyter里运行torch.cuda.is_available(),显示True,在pycharm中运行却显示false。
文章目录 问题概述1、在Jupyter中GPU运行true2、在pycharm中GPU运行false3、个人解决方案仅供参考 问题概述 在jupyter里运行torch.cuda.is_available(),显示True,在pycharm中运行却显示false。原因在于jupyter 运行环境和pycharm 运行环境不同…...

Flutter 中的 Scrollbar 小部件:全面指南
Flutter 中的 Scrollbar 小部件:全面指南 在Flutter中,滚动条(Scrollbar)是一种常见的UI组件,用于提供对滚动内容的快速访问和控制。Scrollbar 小部件可以附加到任何可滚动的widget上,如ListView、GridVie…...
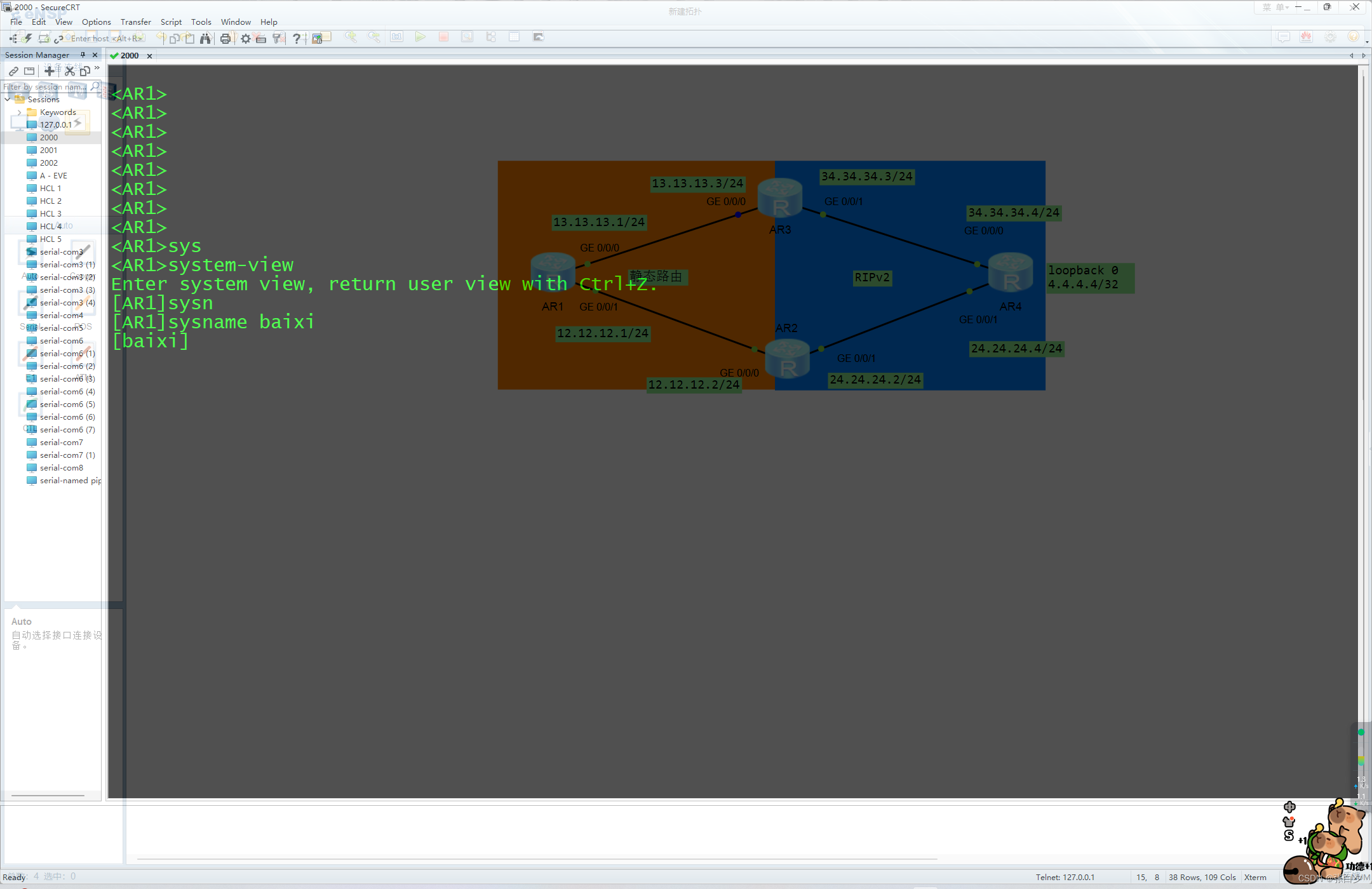
【华为】将eNSP导入CRT,并解决不能敲Tab问题
华为】将eNSP导入CRT,并解决不能敲Tab问题 eNSP导入CRT打开eNSP,新建一个拓扑右键启动查看串口号关联CRT成功界面 SecureCRT连接华为模拟器ensp,Tab键不能补全问题选择Options(选项)-- Global Options (全局选项&#…...

实验二 电子传输系统安全-进展2
上周任务完成情况(代码链接,所写文档等) 重新调通电子公文传输系统部署gmssl学习生成SM2证书学习gmssl中的CTLS实现将数据库从SqlServer迁移到Mysql调试Mysql驱动学习Bouncy Castle 代码链接 Mysql表设计 /* Navicat MySQL Data Transfer…...

JavaScript 获取 HTML 中特定父元素下的子元素
JavaScript 获取 HTML 中特定父元素下的子元素 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <title>查找子元素示例</title> </head> <body><div id"parent"><p&…...

等保服务是一次性服务吗?为什么?怎么理解?
我国等保政策已经严格落地执行,但还有不少企业对于等保服务不是很了解。例如有人问,等保服务是一次性服务吗?为什么?怎么理解?今天我们就来简单回答一下,仅供参考哈! 等保服务是一次性服务吗&…...

全网首发UNIAPP功能多的iapp后台源码
全网首发UNIAPP功能多的iapp后台源码,众所周知UN Dev Assist 后台是一款既不免费又不好用的后台今天直接分享。 搭建教程在里面了,自己查看。 源码下载:https://download.csdn.net/download/m0_66047725/89291994 更多资源下载:…...

【搜索方法推荐】高效信息检索方法和实用网站推荐
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

面试被问到不懂的东西,是直接说不懂还是坚持狡辩一下?
大家好,我是瑶琴呀。 面试被问到不懂的东西,是直接说不懂还是坚持狡辩一下?这个问题可以转变一下,如果你顺利拿到 offer,公司安排的工作跟你之前的技术和经验不匹配,你还愿意干下去吗? 转变一…...

Flutter 中的 StatefulBuilder 小部件:全面指南
Flutter 中的 StatefulBuilder 小部件:全面指南 在Flutter中,StatefulBuilder是一个高效的小部件,它根据给定的构建函数来构建widget,并在组件树中只对需要重新构建的部分进行更新。这使得它在性能优化方面非常有用,特…...

mail发送接口API如何使用?怎么调用接口?
mail发送接口API的性能怎么样?邮件接口发信的技巧? 为了自动化和集成电子邮件功能到应用程序或系统中,开发人员可以使用各种邮件发送接口API。AokSend将介绍如何使用这些API来发送电子邮件,提高效率和灵活性。 mail发送接口API&…...

DOS学习-目录与文件应用操作经典案例-attrib
新书上架~👇全国包邮奥~ python实用小工具开发教程http://pythontoolsteach.com/3 欢迎关注我👆,收藏下次不迷路┗|`O′|┛ 嗷~~ 目录 一.前言 二.使用 三.案例 一.前言 DOS系统中的attrib命令是一个用于显示或更改文件&#…...

STP简介
一、STP介绍 STP 即生成树协议(Spanning Tree Protocol)一种网络协议 STP 主要用于解决以太网中的环路问题。在具有冗余链路的网络环境中,环路可能导致广播风暴、重复帧等不良后果,严重影响网络性能和稳定性。STP 通过在交换机之…...

java调用科大讯飞在线语音合成API --内附完整项目
科大讯飞语音开放平台基础环境搭建 1.用户注册 注册科大讯飞开放平台账号 2.注册好后先创建一个自己的应用 创建完成后进入应用可以看到我们开发需要的三个参数:APPID,APISecret,APIKey 3.因为平台提供的SDK中只支持了简单的中英两种语言语音…...

Vuex 页面刷新数据丢失怎么解决
当Vuex中的数据在页面刷新后丢失时,这通常是因为Vuex的状态数据是保存在运行内存中的,页面刷新会导致Vue实例重新加载,进而Vuex中的数据被重置为初始状态。为了解决这个问题,可以采取以下几种方法: 1. 使用浏览器的本…...

如何使用Cloudways搭建WordPress网站
如今,搭建网站已经变得非常简单,这主要得益于开源的CMS建站系统的兴起。即使是不懂编程的人也能轻松搭建自己的网站,这些CMS系统提供了丰富的主题模板和插件,使用户可以通过简单的拖放和配置操作来建立自己的网站。 WordPress是目…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
