ciscn
ciscn Crypto部分复现
古典密码
先是埃特巴什密码(这个需要进行多次测试),然后base64,再栅栏即可
答案:flag{b2bb0873-8cae-4977-a6de-0e298f0744c3}
_hash
题目:
#!/usr/bin/python2
# Python 2.7 (64-bit version)
# from secret import flag
import os, binascii, hashlib
key = os.urandom(7)
print(hash(key))
print(int(hashlib.sha384(binascii.hexlify(key)).hexdigest(), 16) ^ int(binascii.hexlify(flag), 16))
'''
7457312583301101235
13903983817893117249931704406959869971132956255130487015289848690577655239262013033618370827749581909492660806312017
'''
解题分析:
这个要查python2.7版本的hash函数实现源码(找不到啊/_ \),看了看wp
源码在这:py27哈希 ·PyPI的
分析一下实现原理
部分源码:if isinstance(value, tuple):return Hash.thash(value)if isinstance(value, float):return Hash.fhash(value)if isinstance(value, int):return hash(value)if isinstance(value, ("".__class__, u"".__class__, bytes)) or type(value).__name__ == "buffer":return Hash.shash(value) #要哈希的数是字符串则跳到shash函数
def shash(value):length = len(value)if length == 0:return 0mask = 0xffffffffffffffffx = (Hash.ordinal(value[0]) << 7) & maskfor c in value:x = (1000003 * x) & mask ^ Hash.ordinal(c)x ^= length & mask# Convert to C long typex = ctypes.c_long(x).valueif x == -1:x = -2return x
所以hash函数实现的过程是:
def hash(s):mask = 0xffffffffffffffff#64位s = s.encode()x = s[0] << 7for char in s:x = (1000003 * x) & mask ^ charx ^= len(s) & maskreturn x
&mask即模2^64,用来限制位数大小的
那么hash过程写出来即:(key是7位的)
x 0 = s 0 ∗ 2 7 x_0=s_0 *2^7 x0=s0∗27
x 1 = ( 1000003 ∗ x 0 ) m o d 2 64 ⊕ s 0 x_1=(1000003*x_0) \quad mod \quad 2^{64} \quad \oplus s_0 x1=(1000003∗x0)mod264⊕s0
x 2 = ( 1000003 ∗ x 1 ) m o d 2 64 ⊕ s 1 x_2=(1000003*x_1) \quad mod \quad 2^{64} \quad \oplus s_1 x2=(1000003∗x1)mod264⊕s1
x 3 = ( 1000003 ∗ x 2 ) m o d 2 64 ⊕ s 2 x_3=(1000003*x_2) \quad mod \quad 2^{64} \quad \oplus s_2 x3=(1000003∗x2)mod264⊕s2
以此类推,最后得到:
x = x 7 ⊕ l e n g t h m o d 2 64 x=x_7 \oplus length \quad mod \quad 2^{64} x=x7⊕lengthmod264
现在我们知道hash后的数值即x,需要推出x0,那么进行一个逆过程
x 7 = x ⊕ l e n g t h m o d 2 64 x_7=x \oplus length \quad mod \quad 2^{64} x7=x⊕lengthmod264
x 6 = x 7 ⊕ s 2 ∗ 100000 3 − 1 m o d 2 64 x_6= x_7\oplus s_2*1000003^{-1} \quad mod \quad 2^{64} x6=x7⊕s2∗1000003−1mod264
依次类推,得到x:
x 0 = x 1 ⊕ s 0 ∗ 100000 3 − 1 m o d 2 64 x_0=x_1 \oplus s_0 *1000003^{-1} \quad mod \quad 2^{64} x0=x1⊕s0∗1000003−1mod264
但是我们只有key,s0-s7都是明文中的,所以这里有个中间相遇攻击
中间相遇攻击的思路在于,假设明文key是
abcdefg我们从前面加密4个字符,即加密到x4,并把他作为元组记录下来。
再把得到的密文从后面逆向,逆到x4,如果和前面的对应上了,即爆破出key
(不是很懂)
贴下别的师傅的脚本(还需要再看看,等我后面做个补充)
from itertools import product
from Crypto.Util.number import *
from tqdm import trangemask = 0xffffffffffffffff
inv = inverse(1000003,2**64)
x7 = 7457312583301101235
cipher = 13903983817893117249931704406959869971132956255130487015289848690577655239262013033618370827749581909492660806312017table = {}
for i in trange(256):# 这是第一个字符for tmp in product([i for i in range(256)],repeat=3):# 下面便是hash的实现,但是我们只乘上3个字符x = (i << 7) & mask x = (1000003 * x) & mask ^ ipre = list(tmp)for char in pre:x = (1000003 * x) & mask ^ chartable[x] = pre# 记录下来for tmp in product([i for i in range(256)],repeat=3):tail = list(tmp)x7 = (x7 ^ 7) & maskx6 = (x7 ^ tail[-1]) * inv & maskx5 = (x6 ^ tail[-2]) * inv & maskx4 = (x5 ^ tail[-3]) * inv & maskif x4 in table.keys():print(i,table[x4],tail)# 93 [140, 240, 63] [90, 8, 82]break要跑2.5小时(震惊)
有了key,就直接异或回去即可
import hashlib
import binasciim = [93,140,240,63,90,8,82]
key = b""
for i in m:key += long_to_bytes(i)flag = long_to_bytes(int(hashlib.sha384(binascii.hexlify(key)).hexdigest(), 16) ^ cipher)
print(flag)
# flag{bdb537aa-87ef-4e95-bea4-2f79259bdd07}2024CISCN | DexterJie’Blog
后面的题我正在努力中
相关文章:

ciscn
ciscn Crypto部分复现 古典密码 先是埃特巴什密码(这个需要进行多次测试),然后base64,再栅栏即可 答案:flag{b2bb0873-8cae-4977-a6de-0e298f0744c3} _hash 题目: #!/usr/bin/python2 # Python 2.7 (6…...
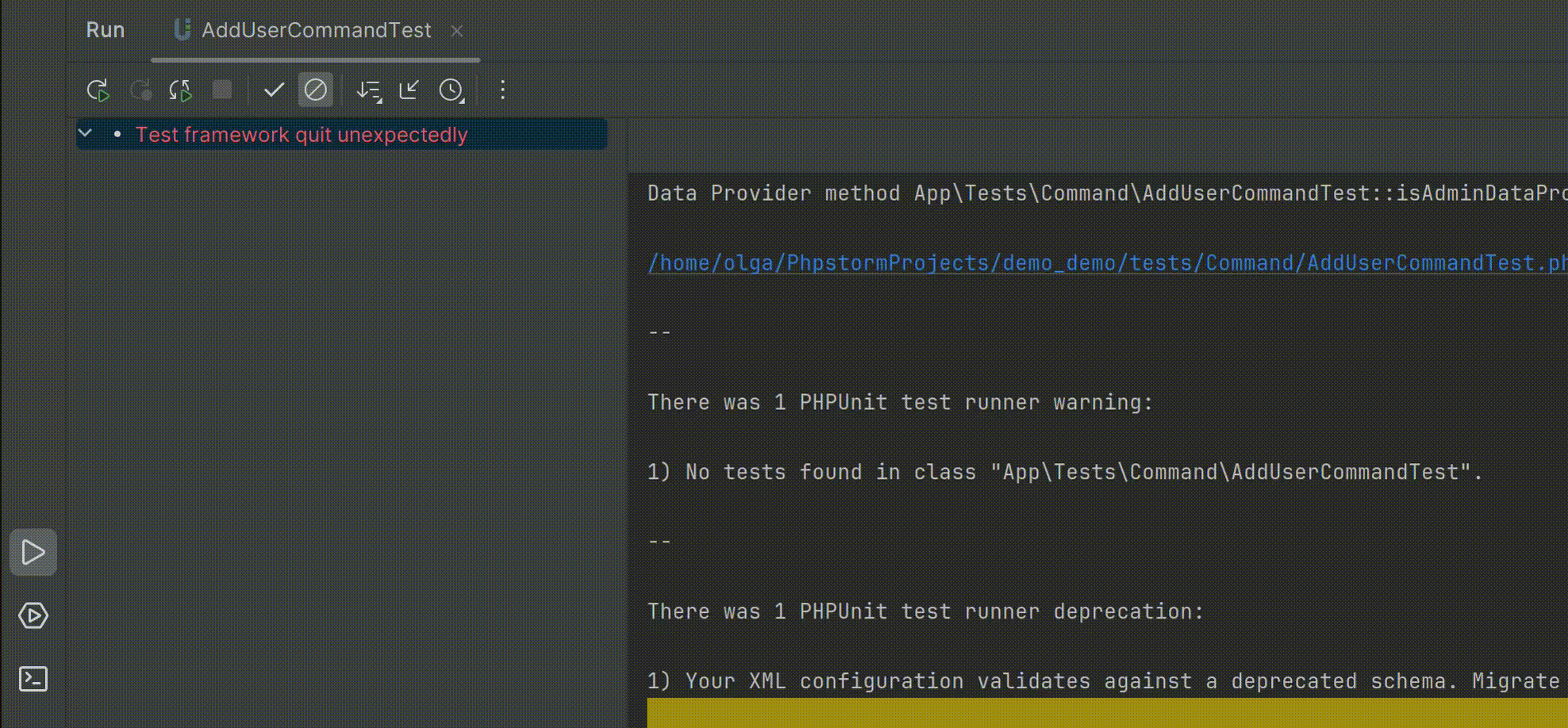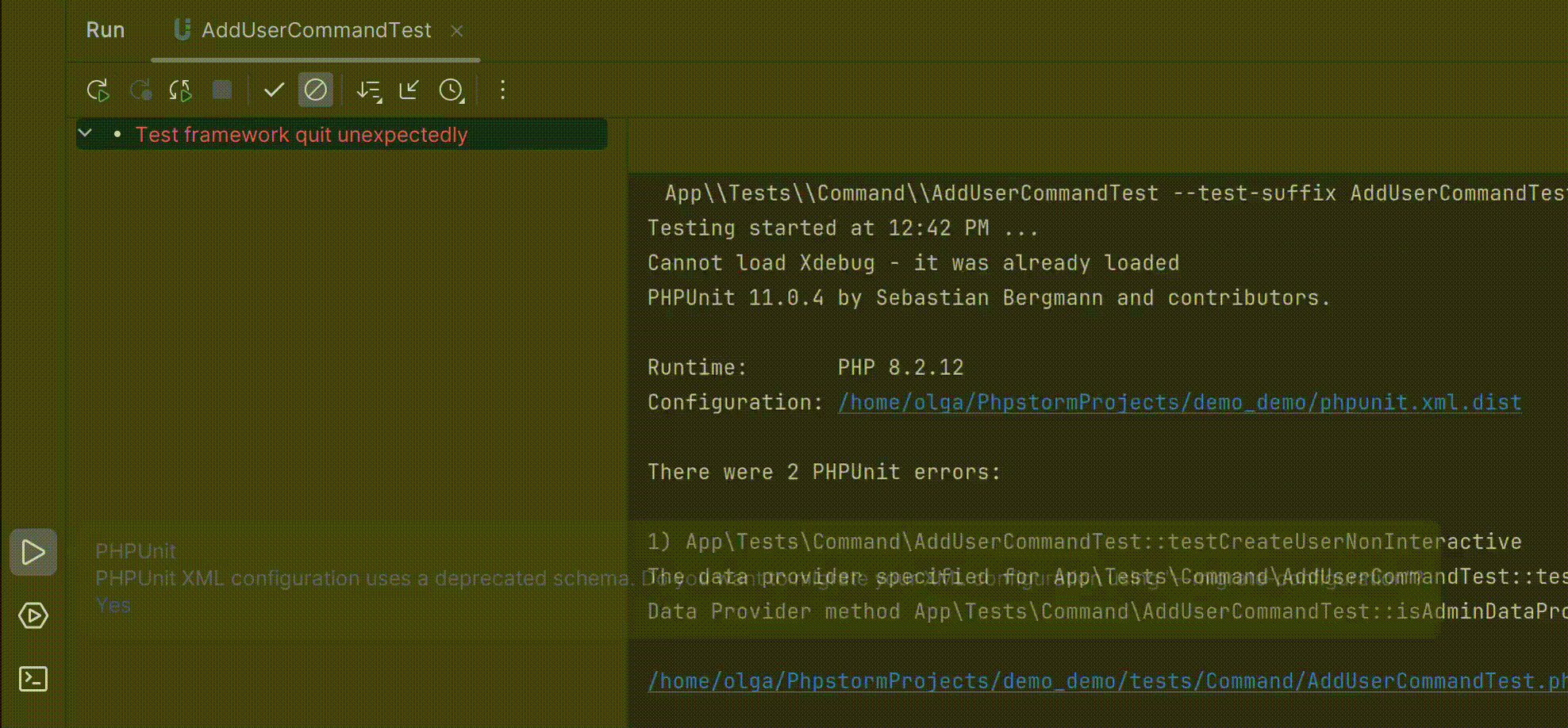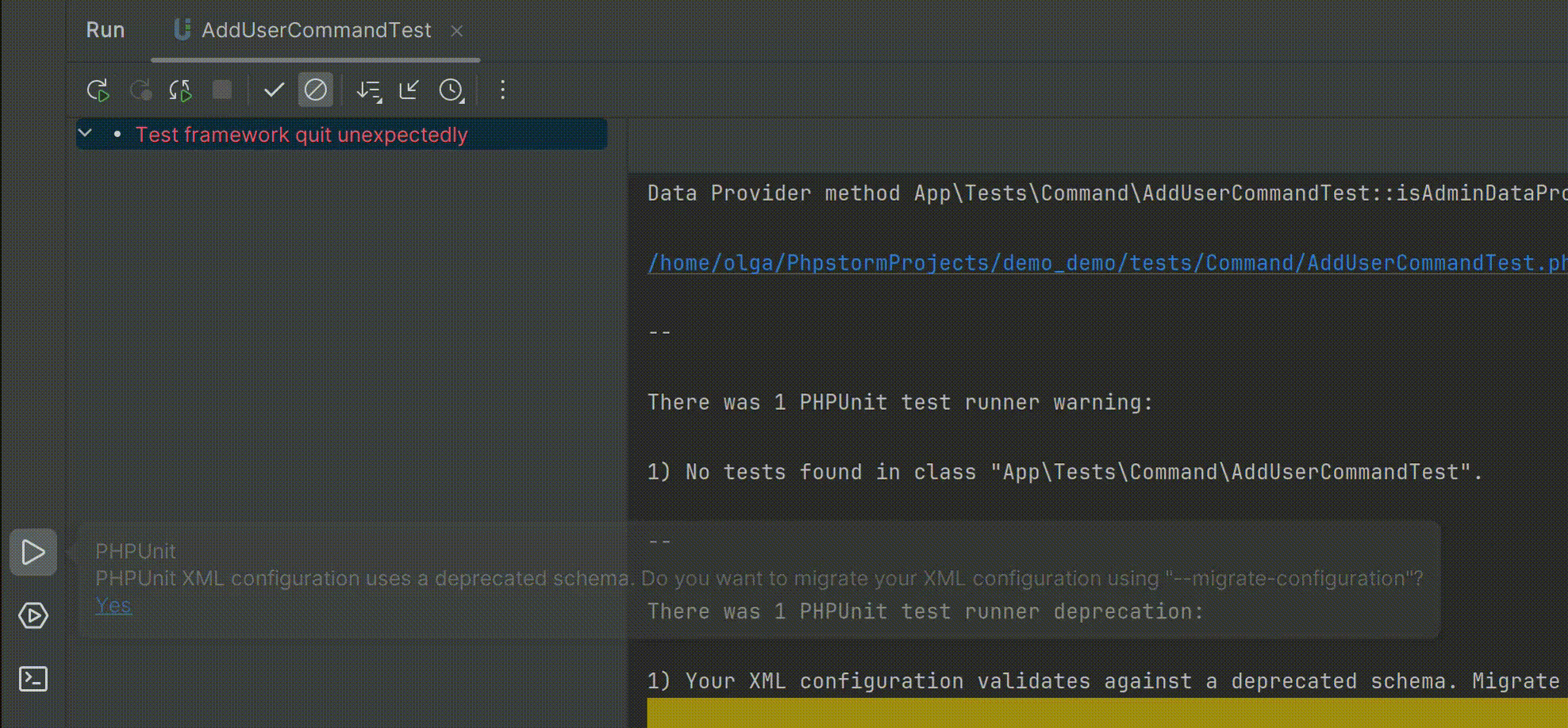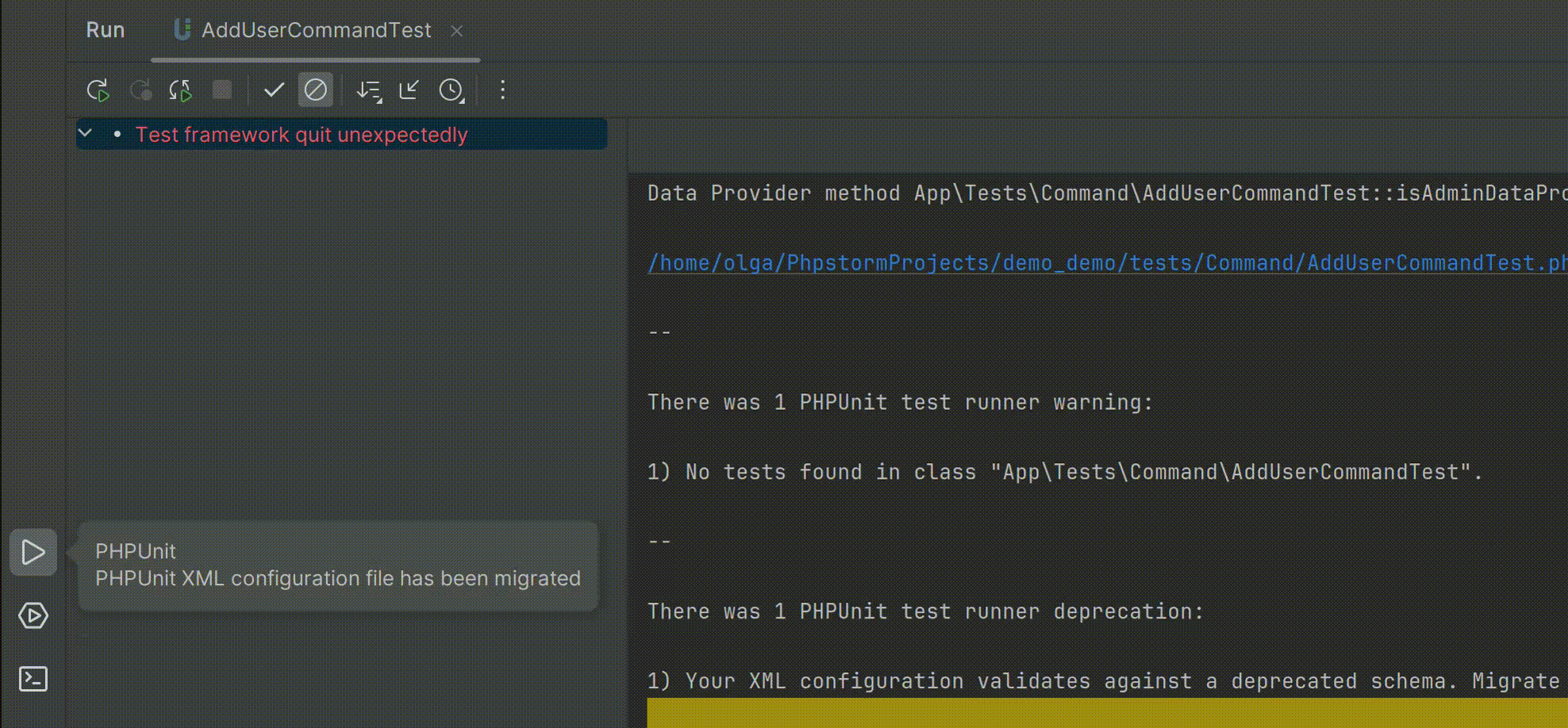
智能的PHP开发工具PhpStorm v2024.1全新发布——支持PHPUnit 11.0
PhpStorm是一个轻量级且便捷的PHP IDE,其旨在提高用户效率,可深刻理解用户的编码,提供智能代码补全,快速导航以及即时错误检查。可随时帮助用户对其编码进行调整,运行单元测试或者提供可视化debug功能。 立即获取PhpS…...
Vue2+Element 封装评论+表情功能
有需要的小伙伴直接拿代码即可,不需要下载依赖,目前是初始版本,后期会进行代码的优化。 评论组件如下: 创建 comment.vue 文件。 表情组件 VueEmoji.vue 在评论组件中使用。 <template><div class"comment"…...

【k8s】存储 pvc 参数列表
相关文章: 【K8s】初识PV和PVC 【k8s】存储 pv 参数列表 【k8s】存储 pvc 参数列表 1. pv概述 2. 参数列表 [rootpaas-controller-3:/home/ubuntu]$ kubectl explain pvc.spec KIND: PersistentVolumeClaim VERSION: v1RESOURCE: spec <Object>DESCRI…...

数据集007:垃圾分类数据集(含数据集下载链接)
数据集简介 本数据拥有 训练集:43685张; 验证集:5363张; 测试集:5363张; 总类别数:158类。 部分代码: 定义数据集 class MyDataset(Dataset):def __init__(self, modetrain, …...
Spring常用注解(超全面)
官网:核心技术SPRINGDOC.CN 提供 Spring 官方文档的翻译服务,可以方便您快速阅读中文版官方文档。https://springdoc.cn/spring/core.html#beans-standard-annotations 1,包扫描组件标注注解 Component:泛指各种组件 Controller、…...

HQL面试题练习 —— 合并活动日期
目录 1 题目2 建表语句3 题解 1 题目 已知有表记录了每个大厅的活动开始日期和结束日期,每个大厅可以有多个活动。请编写一个SQL查询合并在同一个大厅举行的所有重叠的活动,如果两个活动至少有一天相同,那他们就是重叠的,请将他们…...

基于SVm和随机森林算法模型的中国黄金价格预测分析与研究
摘要 本研究基于回归模型,运用支持向量机(SVM)、决策树和随机森林算法,对中国黄金价格进行预测分析。通过历史黄金价格数据的分析和特征工程,建立了相应的预测模型,并利用SVM、决策树和随机森林算法进行训…...

Host头攻击-使用反向代理服务器或负载均衡器来传递路由信息
反向代理服务器的作用 安全性:反向代理服务器位于Web服务器之前,可以隐藏实际Web服务器的身份和地址,从而增加安全性。它还可以对客户端请求进行过滤和检查,以防止潜在的攻击。负载均衡:反向代理服务器可以将客户端请…...

AWS容器之Amazon ECS
Amazon Elastic Container Service(Amazon ECS)是亚马逊提供的一种完全托管的容器编排服务,用于在云中运行、扩展和管理Docker容器化的应用程序。可以理解为Docker在云中对应的服务就是ECS。...
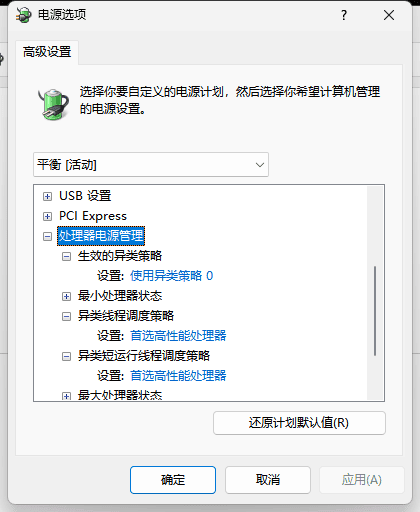
win10/win11 优先调用大核的电源计划性能设置
前言 大小核,即Intel 12代开始的P-core(性能核,一般叫大核)和E-core(能效核,一般叫小核)异核架构。说下个人理解,就是英特尔为了增加cpu性能,但是又因为架构和功耗的限制…...

模型实战(20)之 yolov8分类模型训练自己的数据集
yolov8分类模型训练自己的数据集 yolov8,一个实时快速的端到端的集检测、分割、分类、姿态识别于一体的视觉算法库/框架本文将给出yolov8 分类模型的数据集制作格式及训练流程 1. 环境搭建 关于虚拟环境的搭建真的是老生常谈了,给出一个简单的搭建流程吧#新建虚拟环境 conda …...

好消息!PMP纸质证书可以领取啦!(22年11月至23年8月)
上周五,中国国际人才交流基金会官方发布了《关于2022年11月和2023年3月、5月、8月PMI认证考试证书领取》的通知,具体内容如下: 之前顺利通过PMP/ACP/PgMP考试的同学抓紧时间,在5月24日—6月10日内进入官网上登记领取证书。 PMP考…...
)
select函数(Unix系统)
select函数(Unix系统) 一、函数格式二、参数及返回值2.1 struct fd_set 结构体2.1 struct timeval 结构体2.3 函数参数2.4 返回值 三、用法举例3.1 监控终端输入内容 一、函数格式 #include <sys/time.h>#include <sys/types.h>#include <…...
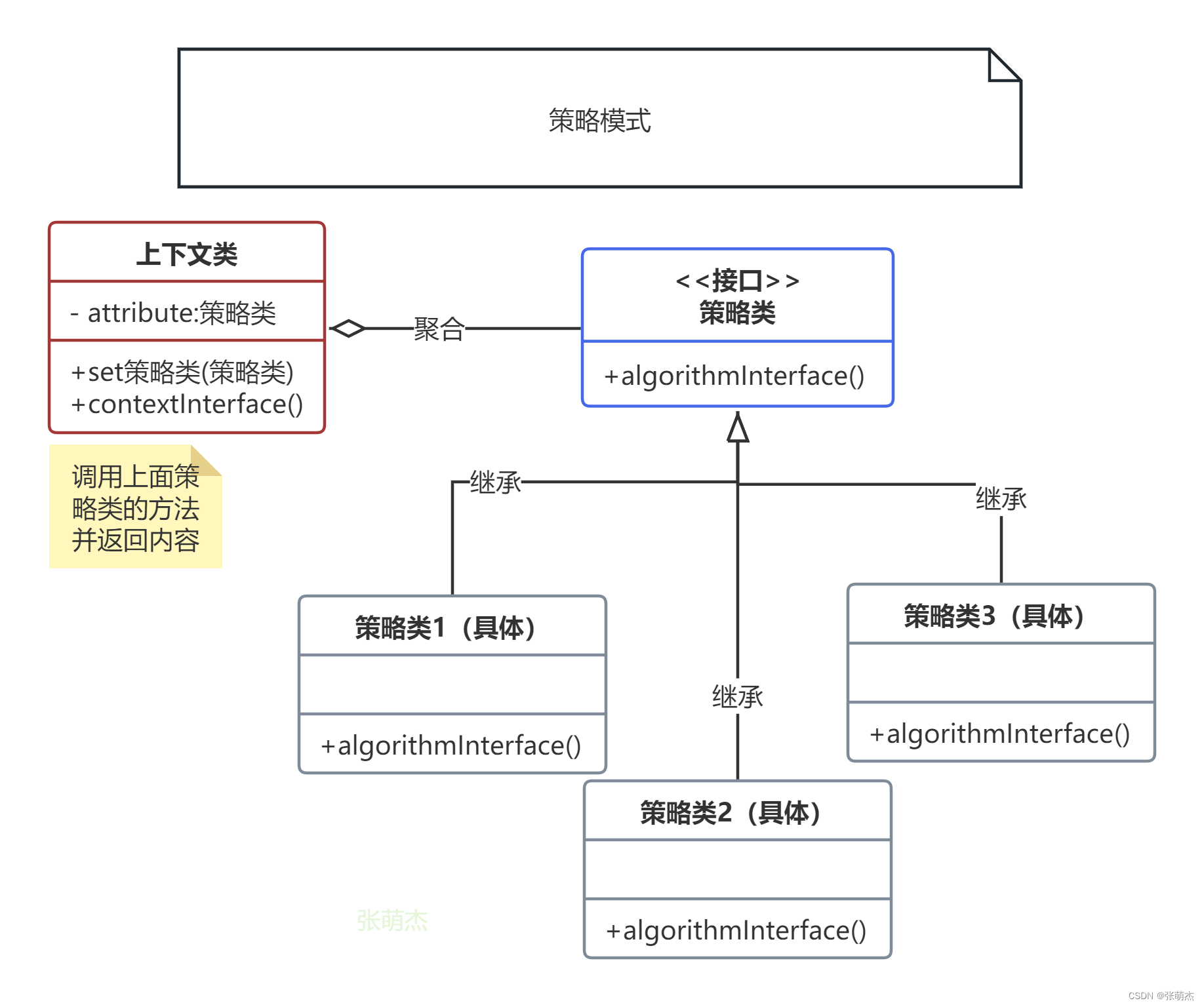
设计模式16——策略模式
写文章的初心主要是用来帮助自己快速的回忆这个模式该怎么用,主要是下面的UML图可以起到大作用,在你学习过一遍以后可能会遗忘,忘记了不要紧,只要看一眼UML图就能想起来了。同时也请大家多多指教。 策略模式(Strategy…...

Putty: 随心御剑——远程启动服务工具plink
一、引言:如何远程控制 也许你会有这样的场景,交互程序(以下简称UI程序)跑在windows端,而控制程序跑在Linux上。我们想要通过windows端 UI程序来启动Linux下面的服务,来一场酣畅淋漓的御剑飞行咋办,难道要自己十年磨一剑,在Linux下编写一个受控服务程序么.计算机科技发…...
Vectorworks 2024 Mac安装包下载Vectorworks 2024安装教程3D建模设计工具
安装 步骤 1,双击下载好的安装包,打开。 2,将G1DXHL.ldf拖到桌面上备用。 3,返回打开的镜像 选择install vectorworks2024 双击打开启动安装程序。电脑就90hi高腰腿疼痛和Y&Aaa9yY 4,输入电脑密码。 5࿰…...

CSRF 攻击详解
什么是csrf攻击? CSRF攻击(Cross-Site Request Forgery,跨站请求伪造)是一种常见的网络攻击方式,它利用网站对用户浏览器的信任,诱使用户在不知情的情况下发送恶意请求。这类攻击通常发生在用户已经通过身…...
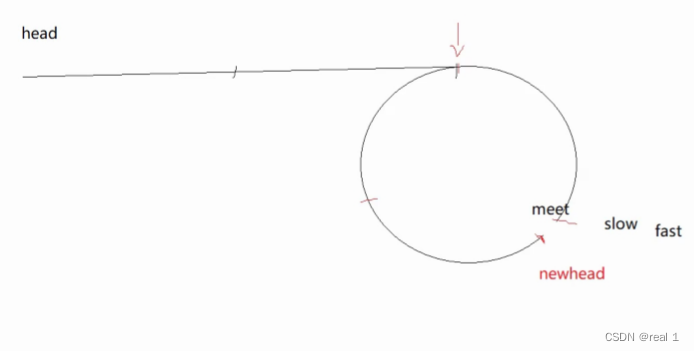
单链表OJ题(课堂总结)
1.链表的带环问题 上图就是一个典型的带环链表 1.1如何判读链表是否带环? 最常见的方法就是利用快慢指针,快指针追加慢指针,当二者相等的时候即可判断链表带环 其实现的代码如下: bool hasCycle(struct ListNode*head) { s…...
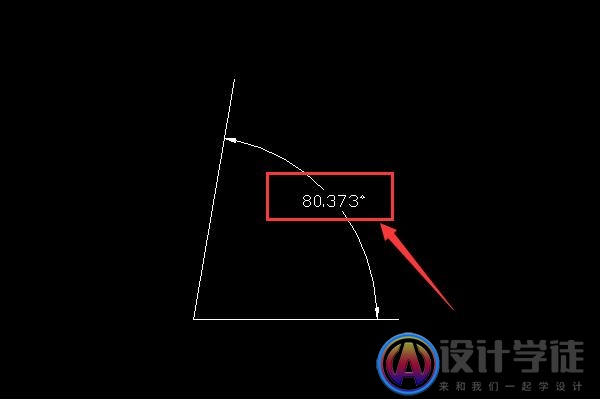
cad角度如何精确到0.1
可以通过更改角度精度的方式把角度的标注精确到小数点后几位,具体方法如下: 1、打开一个CAD文档,在文档中画一个角,如下图: 文章源自设计学徒自学网-https://www.sx1c.com/47920.html 2、给此角进行角度的标注&#…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
