LeetCode - 贪心算法 (Greedy Algorithm) 集合 [分配问题、区间问题]
欢迎关注我的CSDN:https://spike.blog.csdn.net/
本文地址:https://spike.blog.csdn.net/article/details/139242199
贪心算法,是在每一步选择中,都采取当前状态下,最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法,在解决各种问题时被广泛应用,包括数组操作、字符串处理、图论等。
贪心算法包括:分配问题、区间问题。
- 455. 分发饼干 - 分配问题
- 135. 分发糖果 - 分配问题
- 605. 种花问题 - 分配问题
- 406. 根据身高重建队列 - 分配问题
- 435. 无重叠区间 - 区间问题
- 452. 用最少数量的箭引爆气球 - 区间问题
- 763. 划分字母区间 - 区间问题
- 121. 买卖股票的最佳时机 - 区间问题
1. 分配问题
455. 分发饼干 - 分配问题:
class Solution:def findContentChildren(self, g: List[int], s: List[int]) -> int:"""时间复杂度,来自于排序,O(mlogm + nlogn)空间复杂度,类似,O(logm + logn)"""g = sorted(g) # 排序s = sorted(s)n, m = len(g), len(s) # 序列数量i, j = 0, 0while i < n and j < m: # 全部遍历if g[i] <= s[j]: # 判断是否吃饱i += 1 # 孩子满足条件j += 1 # 饼干满足条件return i
135. 分发糖果 - 分配问题:
class Solution:def candy(self, ratings: List[int]) -> int:"""时间复杂度 O(n),空间复杂度 O(n)"""n = len(ratings) # 序列长度res = [1] * n # 每个孩子至少1个糖果# 正序遍历for i in range(1, n):if ratings[i] > ratings[i-1]:res[i] = res[i-1] + 1 # 要是后面+1# print(f"[Info] res: {res}")# 逆序遍历for i in range(n-1, 0, -1):if ratings[i-1] > ratings[i]:# 逆序需要最大值res[i-1] = max(res[i-1], res[i]+1) # print(f"[Info] res: {res}")return sum(res)
605. 种花问题 - 分配问题:
class Solution:def canPlaceFlowers(self, flowerbed: List[int], n: int) -> bool:"""时间复杂度 O(n),空间复杂度 O(1)"""res = 0 # 种花数量m = len(flowerbed) # 花坛长度for i in range(m):# 前面是0,中间是0,最后是0,注意边界if (i==0 or flowerbed[i-1] == 0) and (flowerbed[i] == 0) and (i==m-1 or flowerbed[i+1]==0):res += 1flowerbed[i] = 1return res >= n
406. 根据身高重建队列 - 分配问题,读懂题,根据 -p[0] 和 p[1] 排序,再进行插入,根据 p[1],进行插入。
class Solution:def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:"""插入之前的位置时间O(n^2),空间O(logn)"""# p[0] 从大到小排序,再次根据 p[1] 从小到大排序people.sort(key=lambda x: (-x[0], x[1])) # print(f"[Info] people: {people}")n = len(people) # 人数res = []for p in people:# print(f"[Info] res: {res}")# 根据 p 值的第2位 [正好有k个人],进行排序插入res.insert(p[1], p) # 在p[1]前一个位置插入return res
2. 区间问题
435. 无重叠区间 - 区间问题
class Solution:def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:"""时间复杂度 O(nlogn) 空间复杂度 O(logn)"""# 根据 end 值排序intervals = sorted(intervals, key=lambda x: x[1])# print(f"[Info] intervals: {intervals}")n = len(intervals)res = 0prev = intervals[0][1] # 第1个值的末尾值for i in range(1, n): # 从第2个值开始if intervals[i][0] < prev: # 前值小于后值res += 1 # 相交else:prev = intervals[i][1] # 遍历下一个return res
452. 用最少数量的箭引爆气球 - 区间问题,435 题的变换
class Solution:def findMinArrowShots(self, points: List[List[int]]) -> int:"""区间类型题,与 435 类似时间复杂度 O(nlogn),空间复杂度 O(logn)"""# 尾部排序points = sorted(points, key=lambda x: x[1])n = len(points)prev = points[0][1] # 前值res = 0for i in range(1, n):if prev >= points[i][0]:res += 1 # 重叠值,即1箭射中2个else:prev = points[i][1]return n - res # 最终值是差值
763. 划分字母区间 - 区间问题,记录字母最后出现的位置,与之前最大位置比较。
class Solution:def partitionLabels(self, s: str) -> List[int]:"""时间复杂度 O(n),空间复杂度 O(len(s))"""n=len(s) # 序列长度last=[0]*26 # 字母数量# 遍历获取最后出现的位置for i in range(n):j=ord(s[i])-ord('a')last[j]=max(i,last[j]) # 字母最后出现的位置start,end=0,0res=[]for i in range(n):j=ord(s[i])-ord('a')# 当前字母j最后出现的位置last[j],与之前end,取最大值end=max(end,last[j])if end==i: # end如果等于ires.append(end-start+1) # 序列长度start=end+1 # 起始位置移动return res
121. 买卖股票的最佳时机 - 区间问题
class Solution:def maxProfit(self, prices: List[int]) -> int:"""时间复杂度 O(n),空间复杂度 O(1)"""n=len(prices) # 全部数量res=0 # 结果for i in range(1,n):# 累加区间价格res+=max(0,prices[i]-prices[i-1])return res
相关文章:
LeetCode - 贪心算法 (Greedy Algorithm) 集合 [分配问题、区间问题]
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/139242199 贪心算法,是在每一步选择中,都采取当前状态下,最好或最优(即最有利)的选择&…...
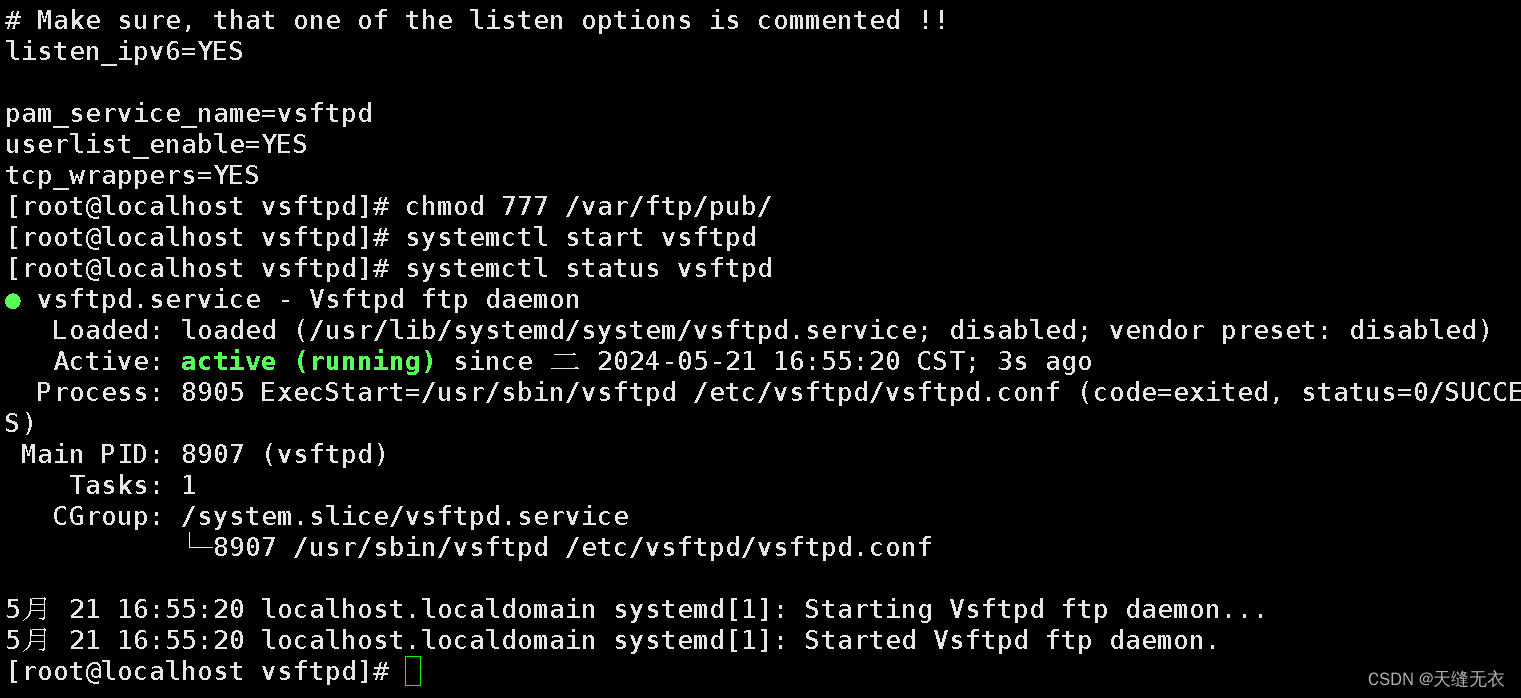
Linux中ftp配置
一、ftp协议 1、端口 ftp默认使用20、21端口 20端口用于建立数据连接 21端口用于建立控制连接 2、ftp数据连接模式 主动模式:服务器主动发起数据连接 被动模式:服务器被动等待数据连接 二、ftp安装 yum install -y vsftpd #---下…...
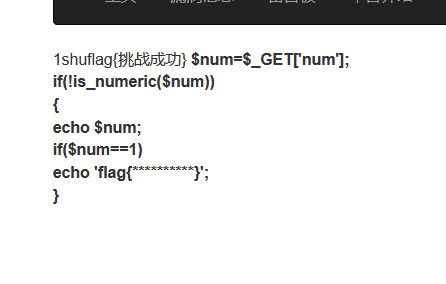
BWVS 靶场测试
一、PHP弱类型 is_numeric() 输入:127.0.0.1/BWVS/bug/php/code.php # 1、源代码分析 如果num不是数字,那么就输出num,同时如果num1,就输出flag。即num要是字符串又要是数字 # 2、函数分析: is_numeric()函数&…...
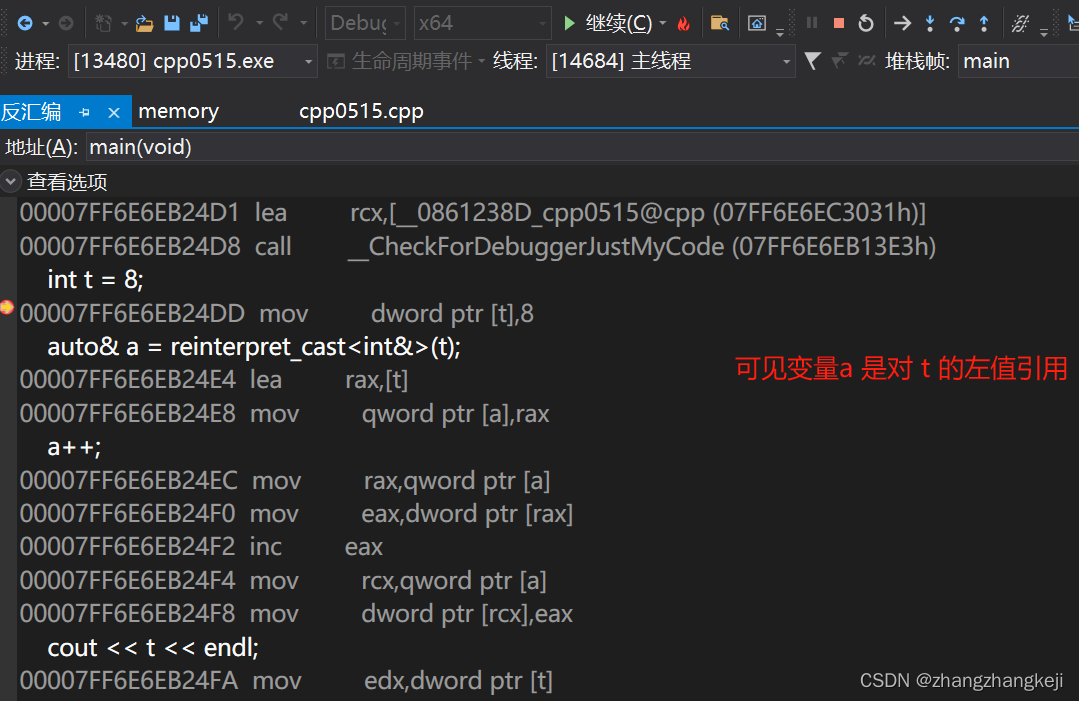
c++ 里重解释转换之于引用 reinterpret_cast< long >
今天遇到了这一很新奇的写法。模糊中记得王老师也这么讲过。c 里四大转换。把数据重解释为原来数据的引用。虽然也可以直接定义对变量的引用。测试如下: 咱们从反汇编再了解下 c 编译器是怎么处理这种写法的: 谢谢...
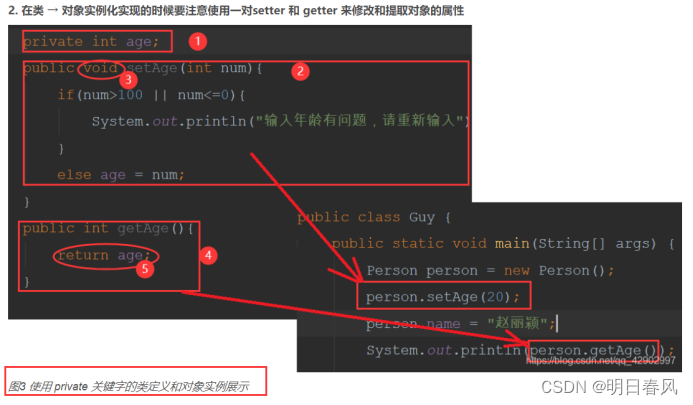
JAVASE2
封装的步骤: 1、所有属性私有化,使用private关键字进行修饰,private表示私有的,修饰的所有数据只能在本类中访问 2、对外提供简单入口:比如说被private修饰的成员变量,在其他类中只能通过getXxx/setXxx方法…...

ora-00392 ora-00312错误处理
检查当前日志组状态 对日志组进行clear操作 重新开库无报错...

网页、h5默认滚动条样式重构
文章目录 前言一、使用步骤1、在想要滚动的元素上设置相应的css类名2.设置样式 总结 前言 此文章用于,让我自己快速设置 浏览器、h5 默认滚动条样式…… 一、使用步骤 1、在想要滚动的元素上设置相应的css类名 代码如下: <div class"list scro…...

香橙派AIpro测评上手指南
一、前言 首先非常荣幸受到邀请参加本次香橙派开发板的测评活动,除了令人眼前一亮,做工非常精细的开发板,举办方还非常贴心地准备了散热套件,以及烧录好系统的TF卡,甚至准备了电源适配器,数据线࿱…...

GBDT 算法【python,机器学习,算法】
GBDT 即 Gradient Boosting Decision Tree 梯度提升树, 是一种迭代的决策树算法,又叫 MART(Multiple Additive Regression Tree), 它通过构造一组弱的学习器(树),然后把多棵决策树的结果累加起来作为最终的预测输出。该算法将决策…...
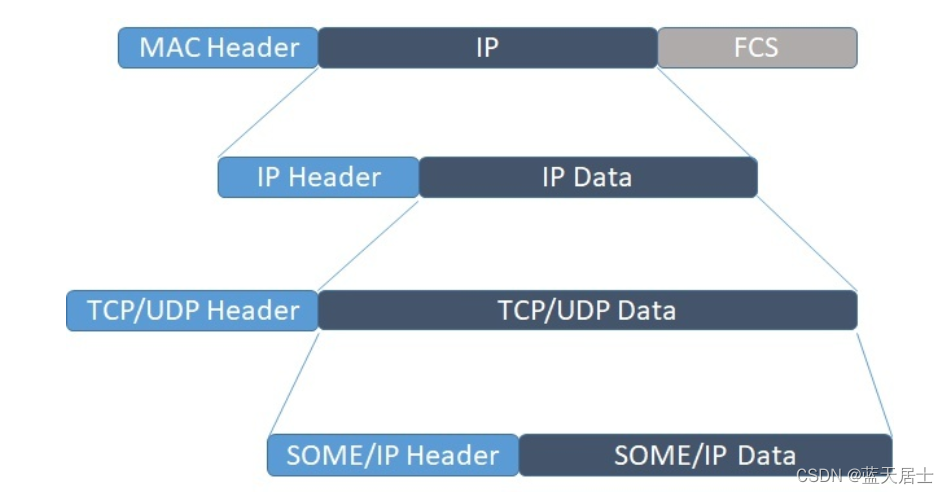
软考 系统架构设计师系列知识点之SOME/IP与DDS(3)
接前一篇文章:软考 系统架构设计师系列知识点之SOME/IP与DDS(2) 本文内容参考: 车载以太网 - SOME/IP简介_someip-CSDN博客 https://zhuanlan.zhihu.com/p/369422441 什么是SOME/IP?_someip-CSDN博客 SOME/IP 详解系列&#…...

将AI大模型装进你的手机,你愿意么?
大数据产业创新服务媒体 ——聚焦数据 改变商业 AI大模型的发展,有两个方向,一个是模型越做越大,以规模来提升性能。还有一个重要的方向,就是通过将模型做小,来嵌入手机、电脑等计算终端,这同样是值得关注…...

前端面试题12-22
12 Proxy是什么,有什么作用? Proxy 是 ES6 (ECMAScript 2015) 引入的一种元编程特性。它允许你创建一个对象,该对象可以拦截和定义基本操作(例如属性查找、赋值、枚举、函数调用等)。Proxy 提供了一种机制,…...

【论文解读】Performance of AV1 Real-Time Mode
论文下载地址:Performance of AV1 Real-Time Mode 时间:2020.10 级别:IEEE 作者:Ludovic Roux 摘要 背景:COVID-19疫情增加了对数字互动的需求,使得实时或低延迟编解码器变得更加重要。现状:大多数编解码器,包括AV1,主要关注于编码效率,这是视频点播(VOD)的主要改…...

java处理中文脱敏
方法一,简单的,不计算文字长度去设置脱敏 public static String dataDesensitization1(String content){String regex "(.{2}).*(.{2})";return ReUtil.replaceAll(content, regex, matcher -> {try {if (CharSequenceUtil.isBlank(match…...

【Linux网络】端口及UDP协议
文章目录 1.再看四层2.端口号2.1引入linux端口号和进程pid的区别端口号是如何生成的传输层有了pid还设置端口号端口号划分 2.2问题2.3netstat 3.UDP协议3.0每学一个协议 都要讨论一下问题3.1UDP协议3.2谈udp/tcp实际上是在讨论什么? 1.再看四层 2.端口号 端口号(Po…...
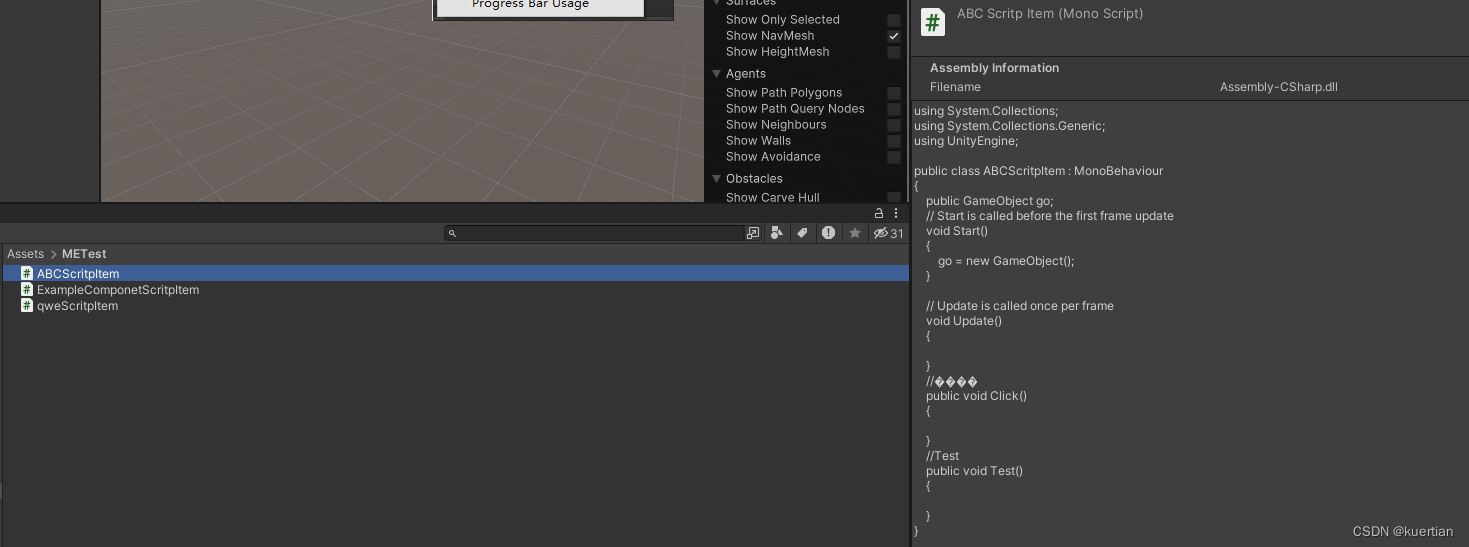
Unity 生成模版代码
1、创建模版代码文本 using System.Collections; using System.Collections.Generic; using UnityEngine;public class ClassNameScritpItem : MonoBehaviour {public GameObject go;// Start is called before the first frame updatevoid Start(){go new GameObject();}// …...

【ai】chatgpt的plugin已经废弃
发现找不到按钮,原来是要申请: https://openai.com/index/chatgpt-plugins/ 发现申请已经跳转了,好像是废弃了? 不接受新插件了,但是openai的api 是可以继续用的。 https://openai.com/waitlist/plugins/We are no longer accepting new Plugins, builders can now create…...

2024年03月 Python(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
Python等级考试(1~6级)全部真题・点这里 一、单选题(共25题,共50分) 第1题 运行如下代码,若输入整数3,则最终输出的结果为?( ) def f(x):if x==1:s=1else:s...

多旋翼无人机机场考哪些内容?
多旋翼无人机机场考试的内容主要包括理论和实飞两部分。 理论考试主要涵盖无人机相关的知识,包括无人机的原理、结构、操作规范等。 实飞考试则主要考察飞行技能,包括飞行操作、航线规划、飞行稳定性等。 具体来说,实飞部分可能包括使用GPS…...

【前端每日基础】day23——箭头函数
箭头函数是ES6(ECMAScript 2015)引入的一种新的函数表达式语法。相比传统函数,箭头函数有简洁的语法,并且不绑定自己的this、arguments、super或new.target。以下是详细介绍箭头函数的各个方面: 基本语法 单参数箭头函…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
