使用numpy手写一个神经网络
本文主要包含以下内容:
- 推导神经网络的误差反向传播过程
- 使用numpy编写简单的神经网络,并使用iris数据集和california_housing数据集分别进行分类和回归任务,最终将训练过程可视化。
1. BP算法的推导过程
1.1 导入
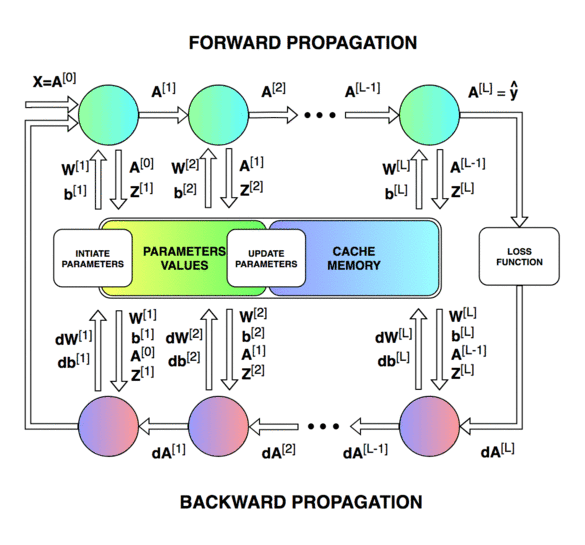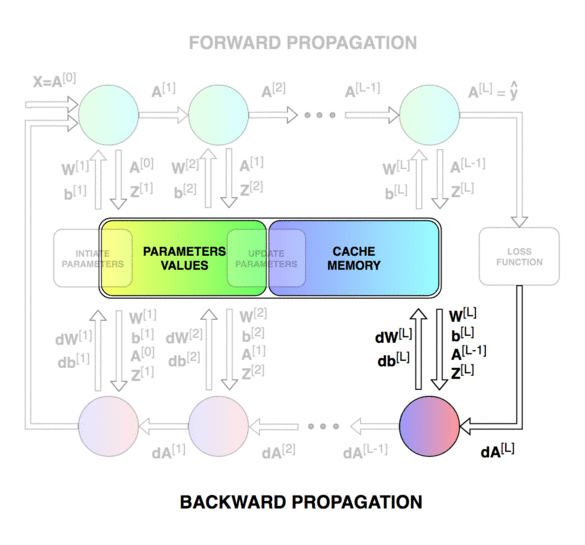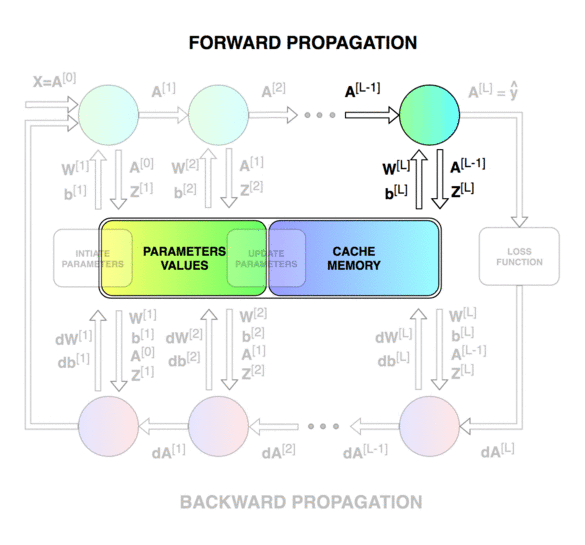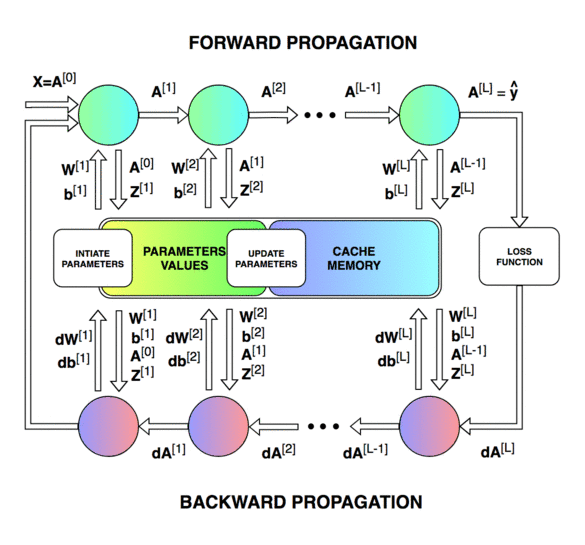
前向传播和反向传播的总体过程。
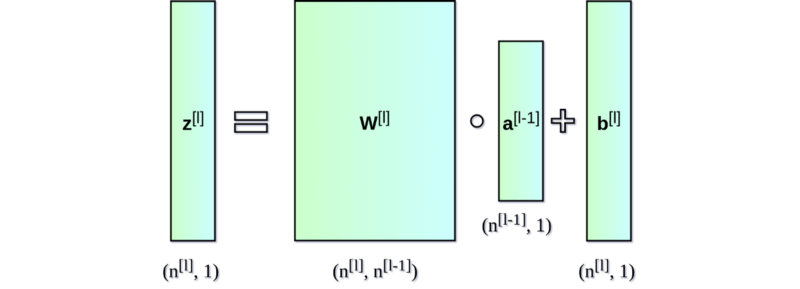
神经网络的直接输出记为 Z [ l ] Z^{[l]} Z[l],表示激活前的输出,激活后的输出记为 A A A。
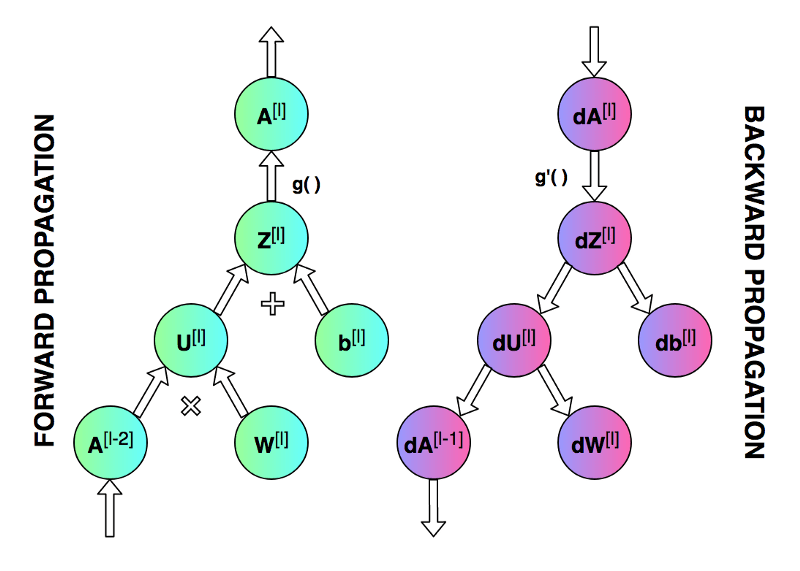
第一个图像是神经网络的前向传递和反向传播的过程,第二个图像用于解释中间的变量关系,第三个图像是前向和后向过程的计算图,方便进行推导,但是第三个图左下角的 A [ l − 2 ] A^{[l-2]} A[l−2]有错误,应该是 A [ l − 1 ] A^{[l-1]} A[l−1]。
1.2 符号表
为了方便进行推导,有必要对各个符号进行介绍
符号表
| 记号 | 含义 |
|---|---|
| n l n_l nl | 第 l l l层神经元个数 |
| f l ( ⋅ ) f_l(\cdot) fl(⋅) | 第 l l l层神经元的激活函数 |
| W l ∈ R n l − 1 × n l \mathbf{W}^l\in\R^{n_{l-1}\times n_{l}} Wl∈Rnl−1×nl | 第 l − 1 l-1 l−1层到第 l l l层的权重矩阵 |
| b l ∈ R n l \mathbf{b}^l \in \R^{n_l} bl∈Rnl | 第 l − 1 l-1 l−1层到第 l l l层的偏置 |
| Z l ∈ R n l \mathbf{Z}^l \in \R^{n_l} Zl∈Rnl | 第 l l l层的净输出,没有经过激活的输出 |
| A l ∈ R n l \mathbf{A}^l \in \R^{n_l} Al∈Rnl | 第 l l l层经过激活函数的输出, A 0 = X A^0=X A0=X |
深层的神经网络都是由一个一个单层网络堆叠起来的,于是我们可以写出神经网络最基本的结构,然后进行堆叠得到深层的神经网络。
于是,我们可以开始编写代码,通过一个类Layer来描述单个神经网络层
class Layer:def __init__(self, input_dim, output_dim):# 初始化参数self.W = np.random.randn(input_dim, output_dim) * 0.01self.b = np.zeros((1, output_dim))def forward(self, X):# 前向计算self.Z = np.dot(X, self.W) + self.bself.A = self.activation(self.Z)return self.Adef backward(self, dA, A_prev, activation_derivative):# 反向传播# 计算公式推导见下方m = A_prev.shape[0]self.dZ = dA * activation_derivative(self.Z)self.dW = np.dot(A_prev.T, self.dZ) / mself.db = np.sum(self.dZ, axis=0, keepdims=True) / mdA_prev = np.dot(self.dZ, self.W.T)return dA_prevdef update_parameters(self, learning_rate):# 参数更新self.W -= learning_rate * self.dWself.b -= learning_rate * self.db# 带有ReLU激活函数的Layer
class ReLULayer(Layer):def activation(self, Z):return np.maximum(0, Z)def activation_derivative(self, Z):return (Z > 0).astype(float)# 带有Softmax激活函数(主要用于分类)的Layer
class SoftmaxLayer(Layer):def activation(self, Z):exp_z = np.exp(Z - np.max(Z, axis=1, keepdims=True))return exp_z / np.sum(exp_z, axis=1, keepdims=True)def activation_derivative(self, Z):# Softmax derivative is more complex, not directly used in this form.return np.ones_like(Z)
1.3 推导过程
权重更新的核心在于计算得到self.dW和self.db,同时,为了将梯度信息不断回传,需要backward函数返回梯度信息dA_prev。
需要用到的公式
Z l = W l A l − 1 + b l A l = f ( Z l ) d Z d W = ( A l − 1 ) T d Z d b = 1 Z^l = W^l A^{l-1} +b^l \\A^l = f(Z^l)\\\frac{dZ}{dW} = (A^{l-1})^T \\\frac{dZ}{db} = 1 Zl=WlAl−1+blAl=f(Zl)dWdZ=(Al−1)TdbdZ=1
解释:
从上方计算图右侧的反向传播过程可以看到,来自于上一层的梯度信息dA经过dZ之后直接传递到db,也经过dU之后传递到dW,于是我们可以得到dW和db的梯度计算公式如下:
d W = d A ⋅ d A d Z ⋅ d Z d W = d A ⋅ f ′ ( d Z ) ⋅ A p r e v T \begin{align}dW &= dA \cdot \frac{dA}{dZ} \cdot \frac{dZ}{dW}\\ &= dA \cdot f'(dZ) \cdot A_{prev}^T \\ \end{align} dW=dA⋅dZdA⋅dWdZ=dA⋅f′(dZ)⋅AprevT
其中, f ( ⋅ ) f(\cdot) f(⋅)是激活函数, f ′ ( ⋅ ) f'(\cdot) f′(⋅)是激活函数的导数, A p r e v T A_{prev}^T AprevT是当前层上一层激活输出的转置。
同理,可以得到
d b = d A ⋅ d A d Z ⋅ d Z d b = d A ⋅ f ′ ( d Z ) \begin{align}db &= dA \cdot \frac{dA}{dZ} \cdot \frac{dZ}{db}\\ &= dA \cdot f'(dZ) \\ \end{align} db=dA⋅dZdA⋅dbdZ=dA⋅f′(dZ)
需要仅需往前传递的梯度信息:
d A p r e v = d A ⋅ d A d Z ⋅ d Z A p r e v = d A ⋅ f ′ ( d Z ) ⋅ W T \begin{align}dA_{prev} &= dA \cdot \frac{dA}{dZ} \cdot \frac{dZ}{A_{prev}}\\ &= dA \cdot f'(dZ) \cdot W^T \\ \end{align} dAprev=dA⋅dZdA⋅AprevdZ=dA⋅f′(dZ)⋅WT
所以,经过上述推导,我们可以将梯度信息从后向前传递。
分类损失函数
分类过程的损失函数最常见的就是交叉熵损失了,用来计算模型输出分布和真实值之间的差异,其公式如下:
L = − 1 N ∑ i = 1 N ∑ j = 1 C y i j l o g ( y i j ^ ) L = -\frac{1}{N}\sum_{i=1}^N \sum_{j=1}^C{y_{ij} log(\hat{y_{ij}})} L=−N1i=1∑Nj=1∑Cyijlog(yij^)
其中, N N N表示样本个数, C C C表示类别个数, y i j y_{ij} yij表示第i个样本的第j个位置的值,由于使用了独热编码,因此每一行仅有1个数字是1,其余全部是0,所以,交叉熵损失每次需要对第 i i i个样本不为0的位置的概率计算对数,然后将所有所有概率取平均值的负数。
交叉熵损失函数的梯度可以简洁地使用如下符号表示:
∇ z L = y ^ − y \nabla_zL = \mathbf{\hat{y}} - \mathbf{{y}} ∇zL=y^−y
回归损失函数
均方差损失函数由于良好的性能被回归问题广泛采用,其公式如下:
L = 1 N ∑ i = 1 N ( y i − y i ^ ) 2 L = \frac{1}{N} \sum_{i=1}^N(y_i - \hat{y_i})^2 L=N1i=1∑N(yi−yi^)2
向量形式:
L = 1 N ∣ ∣ y − y ^ ∣ ∣ 2 2 L = \frac{1}{N} ||\mathbf{y} - \mathbf{\hat{y}}||^2_2 L=N1∣∣y−y^∣∣22
梯度计算:
∇ y ^ L = 2 N ( y ^ − y ) \nabla_{\hat{y}}L = \frac{2}{N}(\mathbf{\hat{y}} - \mathbf{y}) ∇y^L=N2(y^−y)
2 代码
2.1 分类代码
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import matplotlib.pyplot as pltclass Layer:def __init__(self, input_dim, output_dim):self.W = np.random.randn(input_dim, output_dim) * 0.01self.b = np.zeros((1, output_dim))def forward(self, X):self.Z = np.dot(X, self.W) + self.b # 激活前的输出self.A = self.activation(self.Z) # 激活后的输出return self.Adef backward(self, dA, A_prev, activation_derivative):# 注意:梯度信息是反向传递的: l+1 --> l --> l-1# A_prev是第l-1层的输出,也即A^{l-1}# dA是第l+1的层反向传递的梯度信息# activation_derivative是激活函数的导数# dA_prev是传递给第l-1层的梯度信息m = A_prev.shape[0]self.dZ = dA * activation_derivative(self.Z)self.dW = np.dot(A_prev.T, self.dZ) / mself.db = np.sum(self.dZ, axis=0, keepdims=True) / mdA_prev = np.dot(self.dZ, self.W.T) # 反向传递给下一层的梯度信息return dA_prevdef update_parameters(self, learning_rate):self.W -= learning_rate * self.dWself.b -= learning_rate * self.dbclass ReLULayer(Layer):def activation(self, Z):return np.maximum(0, Z)def activation_derivative(self, Z):return (Z > 0).astype(float)class SoftmaxLayer(Layer):def activation(self, Z):exp_z = np.exp(Z - np.max(Z, axis=1, keepdims=True))return exp_z / np.sum(exp_z, axis=1, keepdims=True)def activation_derivative(self, Z):# Softmax derivative is more complex, not directly used in this form.return np.ones_like(Z)class NeuralNetwork:def __init__(self, layer_dims, learning_rate=0.01):self.layers = []self.learning_rate = learning_ratefor i in range(len(layer_dims) - 2):self.layers.append(ReLULayer(layer_dims[i], layer_dims[i + 1]))self.layers.append(SoftmaxLayer(layer_dims[-2], layer_dims[-1]))def cross_entropy_loss(self, y_true, y_pred):n_samples = y_true.shape[0]y_pred_clipped = np.clip(y_pred, 1e-12, 1 - 1e-12)return -np.sum(y_true * np.log(y_pred_clipped)) / n_samplesdef accuracy(self, y_true, y_pred):y_true_labels = np.argmax(y_true, axis=1)y_pred_labels = np.argmax(y_pred, axis=1)return np.mean(y_true_labels == y_pred_labels)def train(self, X, y, epochs):loss_history = []for epoch in range(epochs):A = X# Forward propagationcache = [A]for layer in self.layers:A = layer.forward(A)cache.append(A)loss = self.cross_entropy_loss(y, A)loss_history.append(loss)# Backward propagation# 损失函数求导dA = A - yfor i in reversed(range(len(self.layers))):layer = self.layers[i]A_prev = cache[i]dA = layer.backward(dA, A_prev, layer.activation_derivative)# Update parametersfor layer in self.layers:layer.update_parameters(self.learning_rate)if (epoch + 1) % 100 == 0:print(f'Epoch {epoch + 1}/{epochs}, Loss: {loss:.4f}')return loss_historydef predict(self, X):A = Xfor layer in self.layers:A = layer.forward(A)return A# 导入数据
iris = load_iris()
X = iris.data
y = iris.target.reshape(-1, 1)# One hot encoding
encoder = OneHotEncoder(sparse_output=False)
y = encoder.fit_transform(y)# 分割数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定义并训练神经网络
layer_dims = [X_train.shape[1], 100, 20, y_train.shape[1]] # Example with 2 hidden layers
learning_rate = 0.01
epochs = 5000nn = NeuralNetwork(layer_dims, learning_rate)
loss_history = nn.train(X_train, y_train, epochs)# 预测和评估
train_predictions = nn.predict(X_train)
test_predictions = nn.predict(X_test)train_acc = nn.accuracy(y_train, train_predictions)
test_acc = nn.accuracy(y_test, test_predictions)print(f'Training Accuracy: {train_acc:.4f}')
print(f'Test Accuracy: {test_acc:.4f}')# 绘制损失曲线
plt.plot(loss_history)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()输出
Epoch 100/1000, Loss: 1.0983
Epoch 200/1000, Loss: 1.0980
Epoch 300/1000, Loss: 1.0975
Epoch 400/1000, Loss: 1.0960
Epoch 500/1000, Loss: 1.0891
Epoch 600/1000, Loss: 1.0119
Epoch 700/1000, Loss: 0.6284
Epoch 800/1000, Loss: 0.3711
Epoch 900/1000, Loss: 0.2117
Epoch 1000/1000, Loss: 0.1290
Training Accuracy: 0.9833
Test Accuracy: 1.0000
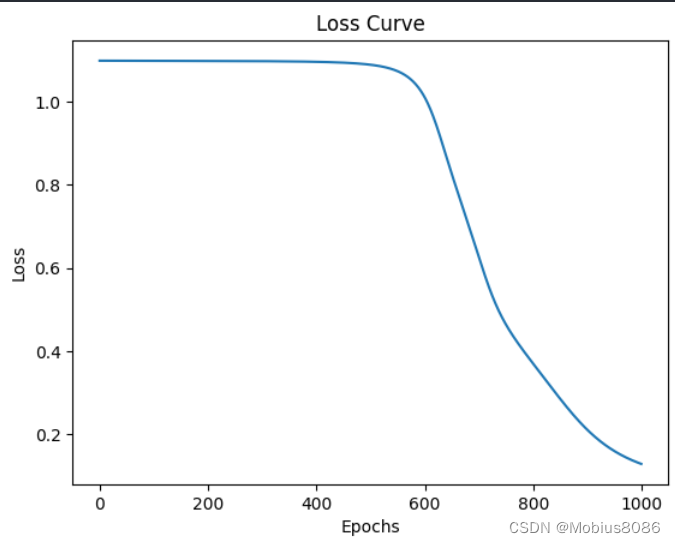
可以看到经过1000轮迭代,最终的准确率到达100%。
回归代码
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housingclass Layer:def __init__(self, input_dim, output_dim):self.W = np.random.randn(input_dim, output_dim) * 0.01self.b = np.zeros((1, output_dim))def forward(self, X):self.Z = np.dot(X, self.W) + self.bself.A = self.activation(self.Z)return self.Adef backward(self, dA, X, activation_derivative):m = X.shape[0]self.dZ = dA * activation_derivative(self.Z)self.dW = np.dot(X.T, self.dZ) / mself.db = np.sum(self.dZ, axis=0, keepdims=True) / mdA_prev = np.dot(self.dZ, self.W.T)return dA_prevdef update_parameters(self, learning_rate):self.W -= learning_rate * self.dWself.b -= learning_rate * self.dbclass ReLULayer(Layer):def activation(self, Z):return np.maximum(0, Z)def activation_derivative(self, Z):return (Z > 0).astype(float)class LinearLayer(Layer):def activation(self, Z):return Zdef activation_derivative(self, Z):return np.ones_like(Z)class NeuralNetwork:def __init__(self, layer_dims, learning_rate=0.01):self.layers = []self.learning_rate = learning_ratefor i in range(len(layer_dims) - 2):self.layers.append(ReLULayer(layer_dims[i], layer_dims[i + 1]))self.layers.append(LinearLayer(layer_dims[-2], layer_dims[-1]))def mean_squared_error(self, y_true, y_pred):return np.mean((y_true - y_pred) ** 2)def train(self, X, y, epochs):loss_history = []for epoch in range(epochs):A = X# Forward propagationcache = [A]for layer in self.layers:A = layer.forward(A)cache.append(A)loss = self.mean_squared_error(y, A)loss_history.append(loss)# Backward propagation# 损失函数求导dA = -(y - A)for i in reversed(range(len(self.layers))):layer = self.layers[i]A_prev = cache[i]dA = layer.backward(dA, A_prev, layer.activation_derivative)# Update parametersfor layer in self.layers:layer.update_parameters(self.learning_rate)if (epoch + 1) % 100 == 0:print(f'Epoch {epoch + 1}/{epochs}, Loss: {loss:.4f}')return loss_historydef predict(self, X):A = Xfor layer in self.layers:A = layer.forward(A)return Ahousing = fetch_california_housing()# 导入数据
X = housing.data
y = housing.target.reshape(-1, 1)# 标准化
scaler_X = StandardScaler()
scaler_y = StandardScaler()
X = scaler_X.fit_transform(X)
y = scaler_y.fit_transform(y)# 分割数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定义并训练神经网络
layer_dims = [X_train.shape[1], 50, 5, 1] # Example with 2 hidden layers
learning_rate = 0.8
epochs = 1000nn = NeuralNetwork(layer_dims, learning_rate)
loss_history = nn.train(X_train, y_train, epochs)# 预测和评估
train_predictions = nn.predict(X_train)
test_predictions = nn.predict(X_test)train_mse = nn.mean_squared_error(y_train, train_predictions)
test_mse = nn.mean_squared_error(y_test, test_predictions)print(f'Training MSE: {train_mse:.4f}')
print(f'Test MSE: {test_mse:.4f}')# 绘制损失曲线
plt.plot(loss_history)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()输出
Epoch 100/1000, Loss: 1.0038
Epoch 200/1000, Loss: 0.9943
Epoch 300/1000, Loss: 0.3497
Epoch 400/1000, Loss: 0.3306
Epoch 500/1000, Loss: 0.3326
Epoch 600/1000, Loss: 0.3206
Epoch 700/1000, Loss: 0.3125
Epoch 800/1000, Loss: 0.3057
Epoch 900/1000, Loss: 0.2999
Epoch 1000/1000, Loss: 0.2958
Training MSE: 0.2992
Test MSE: 0.3071
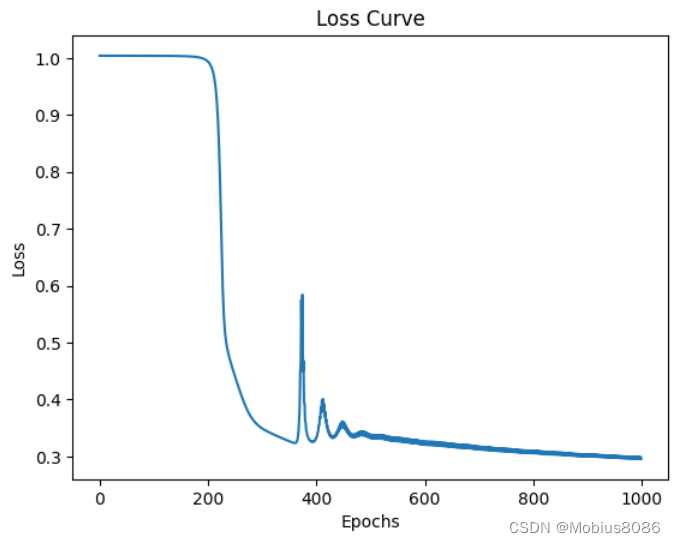
相关文章:

使用numpy手写一个神经网络
本文主要包含以下内容: 推导神经网络的误差反向传播过程使用numpy编写简单的神经网络,并使用iris数据集和california_housing数据集分别进行分类和回归任务,最终将训练过程可视化。 1. BP算法的推导过程 1.1 导入 前向传播和反向传播的总体…...

使用Spring AOP实现接口参数变更前后对比和日志记录
推荐一个程序员的常用工具网站,效率加倍,嘎嘎好用:程序员常用工具云服务器限时免费领:轻量服务器2核4G腾讯云:2核2G4M云服务器新老同享99元/年,续费同价阿里云:2核2G3M的ECS服务器只需99元/年,续费同价记录接口调用前后的参数变化是一个常见的需求,这不仅有助于调试和…...
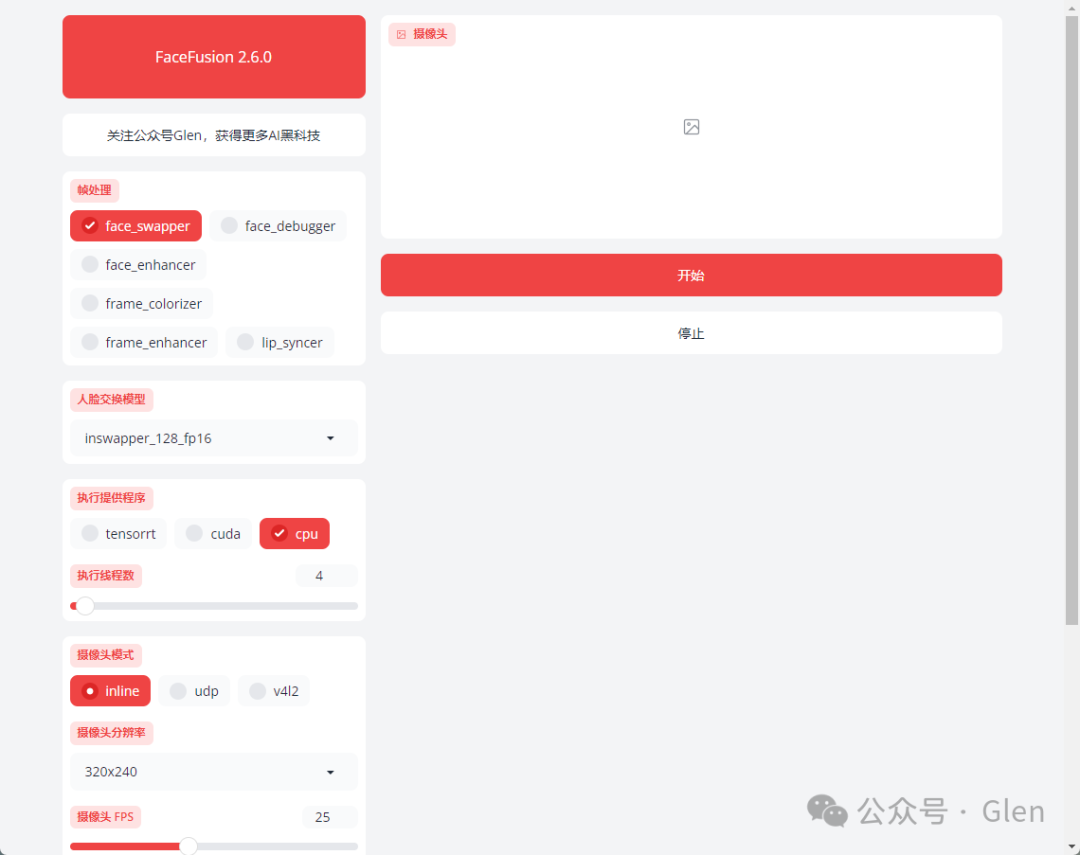
免费无限换脸,火了,图片/视频/直播都行!
最强换脸AI工具Facefusion软件在近期更新到了2.6.0版本,带来了一系列的更新和改进,今天为大家分享一下最新的整合包。 Facefusion2.6.0版本介绍 FaceFusion不仅仅是一款换脸软件,它更是一个多功能的数字人和实时直播助手,真正开启…...

无线领夹麦克风哪个品牌好?本期文章揭秘无线麦克风哪个品牌好用
在当下这个全民皆为媒体的时代大潮中,视频分享已然成为了引领风尚的指向标。在自媒体领域竞争愈发激烈的态势下,若要在这片广阔海洋中扬帆远航,优秀的作品毫无疑问是吸引观众的关键所在。而想要塑造出这样的卓越之作,除了需要创…...
操作系统实验--终极逃课方法
找到图片里的这个路径下的文件 ,结合当前题目名称,把文件内容全部删除,改为print print的内容为下图左下角的预期输出的内容...

C语言实现正弦信号扫频
C语言实现正弦信号扫频 包含必要的头文件:首先,你需要包含 <stdio.h> 和 <math.h> 头文件,分别用于输入输出和数学函数的使用。 定义扫频参数:定义正弦扫频的参数,例如起始频率、结束频率、扫频时间等。 生成正弦波信号:使用正弦函数生成扫频信号,可以根…...
实用篇| huggingface网络不通
之前文章《Transformer原理》中介绍过,Transformers 是由 Hugging Face 开发的一个包,支持加载目前绝大部分的预训练模型。随着 BERT、GPT 等大规模语言模型的兴起,越来越多的公司和研究者采用 Transformers 库来构建应用。 Hugging Face是一家美国公司…...

NLP与训练模型-GPT-3:探索人工智能语言生成的新纪元
在人工智能领域,自然语言处理(NLP)一直是备受关注的研究方向之一。随着深度学习技术的发展,尤其是Transformer模型的出现,NLP领域取得了巨大的进步。其中,由OpenAI推出的GPT-3模型更是引起了广泛的关注和热…...

iOS内购欺诈漏洞
iOS内购欺诈漏洞 1.iOS内购欺诈漏洞概述2.伪造的凭证3.漏洞修复方案 1.iOS内购欺诈漏洞概述 黑产别的App上低价充值(比如1元)换取苹果真实凭证,再在目标App上下单高价(648元)商品,传入该凭证,如…...

【网络服务】正向代理和反向代理到底是什么意思
🚀 个人主页 极客小俊 ✍🏻 作者简介:程序猿、设计师、技术分享 🐋 希望大家多多支持, 我们一起学习和进步! 🏅 欢迎评论 ❤️点赞💬评论 📂收藏 📂加关注 前言 在学习和…...

【算法】记忆化搜索
快乐的流畅:个人主页 个人专栏:《算法神殿》《数据结构世界》《进击的C》 远方有一堆篝火,在为久候之人燃烧! 文章目录 引言一、不同路径二、最长递增子序列三、猜数字大小 ||四、矩阵中的最长递增路径总结 引言 记忆化搜索&…...
博客系统多模块开发
创建工程 创建父工程 删除src目录,在pom.xml添加依赖: <!--统一版本 字符编码--><properties><maven.compiler.source>8</maven.compiler.source><maven.compiler.target>8</maven.compiler.target><project.b…...
pdf阅读器哪个好用?五款PDF阅读器大比拼
pdf阅读器哪个好用?在数字化时代,PDF文档因其跨平台、跨设备的便捷性,已成为工作、学习和生活中不可或缺的一部分。而一款优秀的PDF阅读器,则能极大地提升我们处理PDF文档的效率与体验。今天,就让我们一起探索五款备受…...

C#实现Queue的加锁和解锁
在C#中,可以使用lock语句来对队列进行加锁和解锁,以确保在多线程环境下的线程安全。以下是一个简单的示例: using System; using System.Collections.Generic; using System.Threading;public class ThreadSafeQueue<T> {private read…...
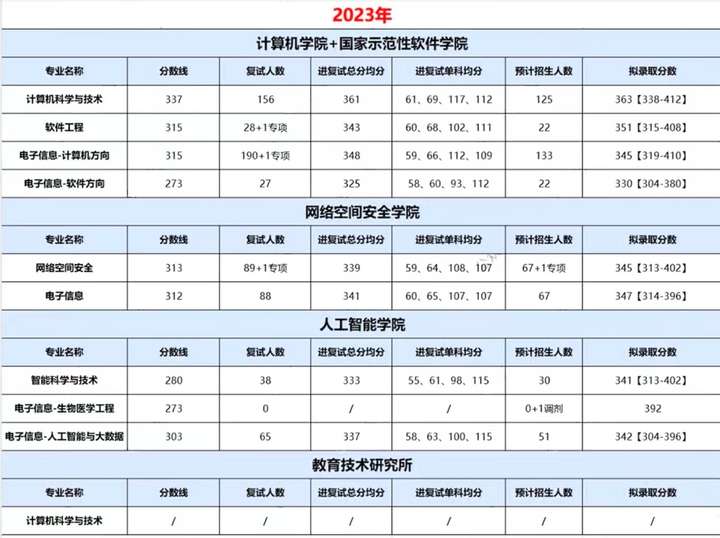
北京邮电大学人工智能考数据结构,均分370!北京邮电大学计算机考研考情分析!
北京邮电大学(Beijing University of Posts and Telecommunications),简称北邮,是中华人民共和国教育部直属、工业和信息化部共建的全国重点大学,位列国家“211工程”、“985工程优势学科创新平台”、“世界一流学科建…...

1. lambda初体验
首先声明一个函数式接口,就只接口内只有一个抽象方法 //函数式接口 public interface Factory {Object getObject();}接口实现类 public class SubClass implements Factory {Overridepublic Object getObject() {return new User();}}User类 public class User …...

C#之显示转换
在C#中显示转换分为三种本别是: 括号强转,parse法,convert法。下面就为大家介绍一下吧!!! 括号强转 作用: 一般情况下 将高精度的类型转换为低精度 语法: 变量类型 变量名 (转换的变量类型名称) 变量; …...
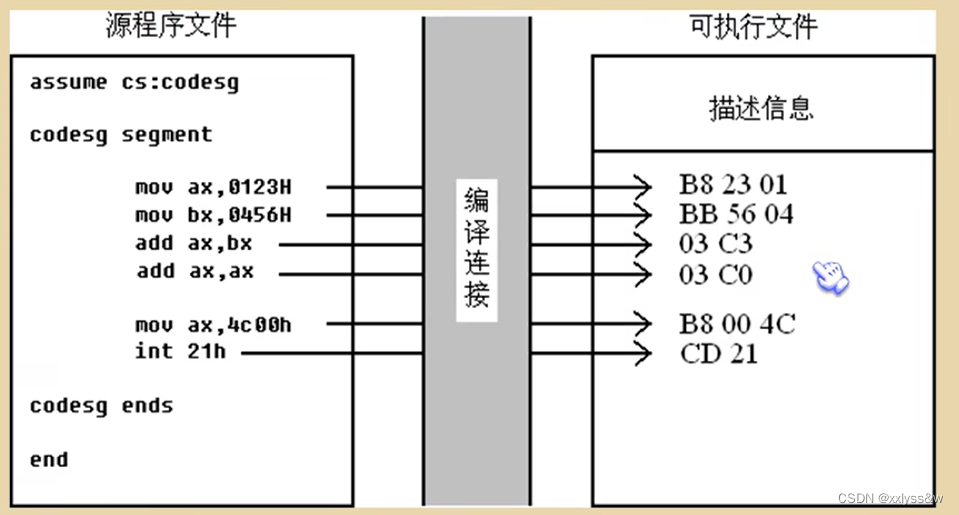
汇编原理(三)编程
源程序: 汇编指令:有对应的机器码与其对应 伪指令:无对应的机器码,是由编译器来执行的指令,编译器根据伪指令来进行相关的编译工作。 ex1:XXX segment、XXX ends这两个是一对成对使用的伪指令,且必须会被用…...
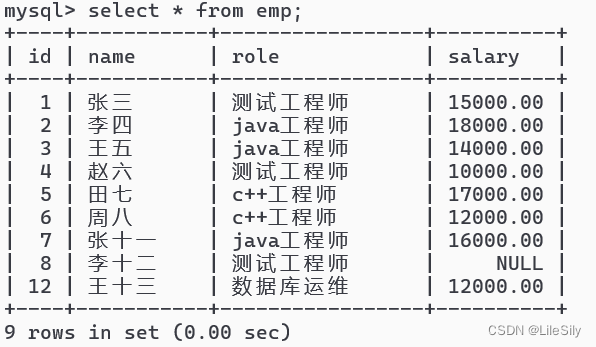
[MySQL数据库] Java的JDBC编程(MySQL数据库基础操作完结)
🌸个人主页:https://blog.csdn.net/2301_80050796?spm1000.2115.3001.5343 🏵️热门专栏:🍕 Collection与数据结构 (91平均质量分)https://blog.csdn.net/2301_80050796/category_12621348.html?spm1001.2014.3001.5482 🧀Java …...

绿色瓶装水“暗战”竞争越发激烈,华润饮料谋上市同时多地扩产能
《港湾商业观察》黄懿 4月23日,纯净水牌“怡宝”母公司华润饮料(控股)有限公司(下称“华润饮料”)向港交所主板提交上市申请,联席保荐人为中银国际、中信证券、美银美林、瑞银集团。 在华润饮料递表不久之…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
