高等数学——微分方程
文章目录
- 概念
- 一阶微分方程
- 可降阶的微分方程
- 高阶线性微分方程
- 线性微分方程解的结构
- 常系数齐次线性微分方程
- 常系数非齐次线性微分方程
概念
- 微分方程:含有未知函数的导数或微分的方程称为微分方程。
- 微分方程的阶:微分方程中所出现的未知函数最高阶导数的阶数,称为微分方程的阶。
- 微分方程的解:满足微分方程的函数称为微分方程的解。
- 微分方程的通解:如果微分方程的解中含有任意常数,且任意常数的个数与微分方程的阶数相同,则称之为微分方程的通解。
- 微分方程的特解:微分方程不含有任何常数的解称为特解。
- 初始条件:确定特解的一组常数称为初始条件。
- 积分曲线:微分方程的一个解在平面上对应的一条曲线,称为该微分方程的积分曲线。
一阶微分方程
一阶微分方程的一般形式:dydx=f(x,y)\frac{dy}{dx}=f(x,y)dxdy=f(x,y)
- 可分离变量的微分方程:能表示为g(y)dy=f(x)dxg(y)dy=f(x)dxg(y)dy=f(x)dx的微分方程称为可分离变量的微分方程。求解的方法是两端积分∫g(y)dy=∫f(x)dx\int g(y)dy=\int f(x)dx∫g(y)dy=∫f(x)dx。
- 齐次微分方程:能表示为dydx=φ(yx)\frac{dy}{dx}=\varphi(\frac{y}{x})dxdy=φ(xy)的微分方程称为齐次微分方程。求解齐次微分方程的一般方法:令u=yxu=\frac{y}{x}u=xy,则dydx=u+xu′\frac{dy}{dx}=u+xu'dxdy=u+xu′,从而将原方程化为xu′=φ(u)−uxu'=\varphi(u)-uxu′=φ(u)−u,此方程为可分离变量的微分方程。
- 一阶线性微分方程(未知函数yyy和y′y'y′都是一次):形如dydx+P(x)y=Q(x)\frac{dy}{dx}+P(x)y=Q(x)dxdy+P(x)y=Q(x)的方程称为一般线性方程。求解一般线性方程的一般方法:常数变易法,或直接利用以下通解公式:y=e−∫P(x)dx[∫Q(x)e∫P(x)dxdx+C]y=e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]y=e−∫P(x)dx[∫Q(x)e∫P(x)dxdx+C]。
可降阶的微分方程
- y(n)=f(x)y^{(n)}=f(x)y(n)=f(x)型的微分方程,可两边同时积分直至将原方程降为一阶微分方程。
- y′′=f(x,y′)y''=f(x,y')y′′=f(x,y′)型的方程。只需令y′=P,y′′=dPdxy'=P,y''=\frac{dP}{dx}y′=P,y′′=dxdP,可将原方程化为一阶微分方程。
- y′′=f(y,y′)y''=f(y,y')y′′=f(y,y′)型的方程。只需令y′=p,y′′=pdpdyy'=p,y''=p\frac{dp}{dy}y′=p,y′′=pdydp,可将原方程化为一阶微分方程。
高阶线性微分方程
线性微分方程解的结构
这里只讨论二阶线性微分方程,其结论可以推广到更高阶的方程,二阶线性微分方程的一般形式为y′′+p(x)y′+q(x)y=f(x)y''+p(x)y'+q(x)y=f(x)y′′+p(x)y′+q(x)y=f(x)这里的p(x),q(x),f(x)p(x),q(x),f(x)p(x),q(x),f(x)均为连续函数,当齐次方程右端的f(x)≡0f(x)≡0f(x)≡0时,称为二阶线性齐次方程,否则就称为二阶线性非齐次方程。
- 齐次方程:y′′=p(x)y′+q(x)y=0①y''=p(x)y'+q(x)y=0①y′′=p(x)y′+q(x)y=0①
- 非齐次方程:y′′+p(x)y′+q(x)y=f(x)②y''+p(x)y'+q(x)y=f(x)②y′′+p(x)y′+q(x)y=f(x)②
如果y1(x)y_1(x)y1(x)和y2(x)y_2(x)y2(x)是齐次方程①的两个线性无关(线性无关的充要条件是它们之比不为常数)解,那么y=C1y1(x)+C2y2(x)y=C_1y_1(x)+C_2y_2(x)y=C1y1(x)+C2y2(x)就是齐次方程①的通解。如果y∗y^*y∗是非齐次方程②的一个特解,y1(x)y_1(x)y1(x)和y2(x)y_2(x)y2(x)是齐次方程①的两个线性无关特解,那么y=C1y1(x)+C2y2(x)+y∗(x)y=C_1y_1(x)+C_2y_2(x)+y^*(x)y=C1y1(x)+C2y2(x)+y∗(x)就是非齐次方程②的通解。如果y1∗(x)y_1^*(x)y1∗(x)和y2∗(x)y_2^*(x)y2∗(x)是非齐次方程②的两个特解,那么y(x)=y2∗(x)−y1∗(x)y(x)=y_2^*(x)-y_1^*(x)y(x)=y2∗(x)−y1∗(x)是齐次方程①的解。如果y1∗(x)y_1^*(x)y1∗(x)和y2∗(x)y_2^*(x)y2∗(x)分别是方程y′′+p(x)y′+q(x)y=f1(x)y''+p(x)y'+q(x)y=f_1(x)y′′+p(x)y′+q(x)y=f1(x)和y′′+p(x)y′+q(x)y=f2(x)y''+p(x)y'+q(x)y=f_2(x)y′′+p(x)y′+q(x)y=f2(x)的特解,则y1∗(x)+y2∗(x)y_1^*(x)+y_2^*(x)y1∗(x)+y2∗(x)是方程y′′+p(x)y′+q(x)y=f1(x)+f2(x)y''+p(x)y'+q(x)y=f_1(x)+f_2(x)y′′+p(x)y′+q(x)y=f1(x)+f2(x)的一个特解。
常系数齐次线性微分方程
二阶带常系数线性齐次微分方程的一般形式为y′′+py′+qy=0③y''+py'+qy=0③y′′+py′+qy=0③其特征方程为r2+pr+1=0r^2+pr+1=0r2+pr+1=0,设r1,r2r_1,r_2r1,r2为该方程的两个根:
- 若r1≠r2r_1≠r_2r1=r2为两个不相等的实特征根,则方程③的通解为y=C1er1x+C2er2xy=C_1e^{r_1x}+C_2e^{r_2x}y=C1er1x+C2er2x
- 若r1=r2r_1=r_2r1=r2为二重实特征根,则方程③的通解为y=(C1+C2x)er1xy=(C_1+C_2x)e^{r_1x}y=(C1+C2x)er1x
- 若r1=a+iβ,r2=a−iβr_1=a+i\beta,r_2=a-i\betar1=a+iβ,r2=a−iβ为一对共轭复根,则方程③的通解为y=eax(C1cosβx+C2sinβx)y=e^{ax}(C_1cos\beta x+C_2sin\beta x)y=eax(C1cosβx+C2sinβx)
常系数非齐次线性微分方程
二阶常系数非齐次微分方程的一般形式为y′′+py′=qy=f(x)④y''+py'=qy=f(x)④y′′+py′=qy=f(x)④
- 若f(x)=Pm(x)eλxf(x)=P_m(x)e^{\lambda x}f(x)=Pm(x)eλx,其中Pm(x)P_m(x)Pm(x)为xxx的mmm次多项式,则方程④的特解可设为y∗=xkQm(x)eλxy^*=x^kQ_m(x)e^{\lambda x}y∗=xkQm(x)eλx其中Qm(x)Q_m(x)Qm(x)是与Pm(x)P_m(x)Pm(x)同次的多项式,kkk是特征方程含根λ\lambdaλ的重复次数。
- 若f(x)=eαx[Pl(1)(x)cosβx+Pn(2)(x)sinβx]f(x)=e^{\alpha x}[P_l^{(1)}(x)cos\beta x+P_n^{(2)}(x)sin\beta x]f(x)=eαx[Pl(1)(x)cosβx+Pn(2)(x)sinβx],其中Pl(1),Pn(2)P_l^{(1)},P_n^{(2)}Pl(1),Pn(2)分别是xxx的lll次和nnn次多项式,则方程④的特解可设为:y∗=xkeax[Rm(1)(x)cosβx+Rm(2)(x)sinβx]y^*=x^ke^{ax}[R^{(1)}_m(x)cos\beta x+R^{(2)}_m(x)sin\beta x]y∗=xkeax[Rm(1)(x)cosβx+Rm(2)(x)sinβx]其中Rm(1)(x)R^{(1)}_m(x)Rm(1)(x)和Rm(2)(x)R^{(2)}_m(x)Rm(2)(x)是两个mmm次多项式,m=max(l,m)m=max(l,m)m=max(l,m)。
- 当α+iβ\alpha+i\betaα+iβ不是方程③的特征根时,取k=0k=0k=0。
- 当α+iβ\alpha+i\betaα+iβ是方程③的特征根时,取k=1k=1k=1。
相关文章:

高等数学——微分方程
文章目录概念一阶微分方程可降阶的微分方程高阶线性微分方程线性微分方程解的结构常系数齐次线性微分方程常系数非齐次线性微分方程概念 微分方程:含有未知函数的导数或微分的方程称为微分方程。微分方程的阶:微分方程中所出现的未知函数最高阶导数的阶…...

JAVA小记-生成PDF文件
项目场景: 例如:项目中需要生成PDF文件 项目使用情况 1、引入pom.xml <!--pdf相关依赖--> <dependency><groupId>com.itextpdf</groupId><artifactId>itextpdf</artifactId><version>5.5.13</version> </dependency>…...
Noah-MP陆面过程模型建模方法与站点、区域模拟
陆表过程的主要研究内容以及陆面模型在生态水文研究中的地位和作用 熟悉模型的发展历程,常见模型及各自特点; Noah-MP模型的原理 Noah-MP模型所需的系统环境与编译环境的搭建方法您都了解吗?? linux系统操作环境您熟悉吗&…...

全国青少年软件编程(Scratch)等级考试一级真题——2019.9
青少年软件编程(Scratch)等级考试试卷(一级)分数:100 题数:37一、单选题(共25题,每题2分,共50分)1.小明在做一个采访的小动画,想让主持人角色说“大家好!”3秒…...
第十四届蓝桥杯三月真题刷题训练——第 6 天
目录 第 1 题:星期计算 问题描述 运行限制 代码: 第 2 题:考勤刷卡 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 代码: 第 3 题:卡片 问题描述 输入格式 输出格式 样…...

安装MySQL数据库8.0服务实例
前言 之前尝试去安装了MySQL5.7的社区版本,今天来安装MySQL8.0的版本,并且以两种方式进行安装,一个是通过RPM包的安装,另一个则是编译的方式。 一. 前期准备 查看服务器IP [rootlocalhost ~]# hostname -I 192.168.161.166 19…...
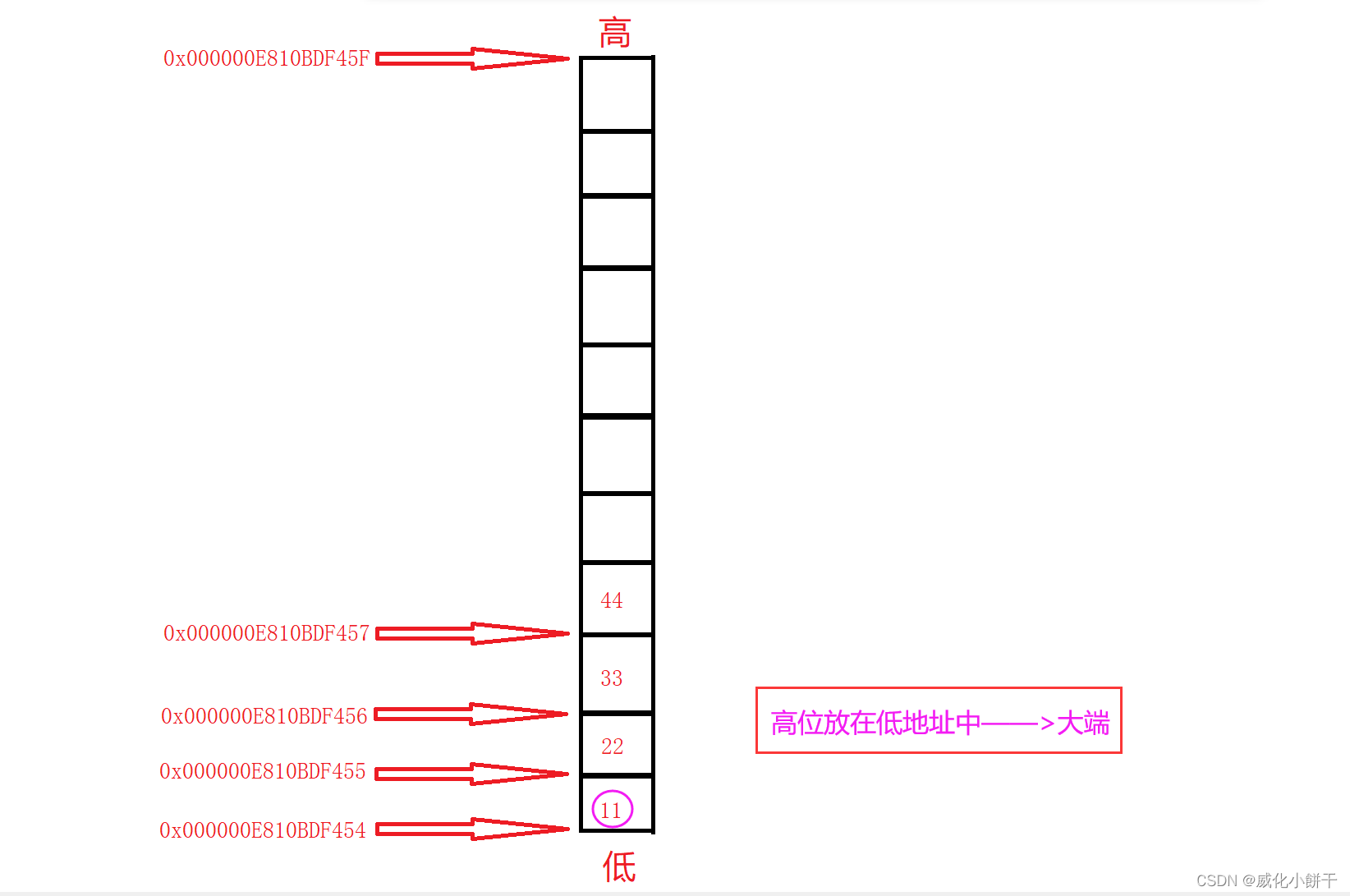
数据的存储--->【大小端字节序】(Big Endian)(Little Endian)
⛩️博主主页:威化小餅干📝系列专栏:【C语言】藏宝图🎏 ✨绳锯⽊断,⽔滴⽯穿!一个编程爱好者的学习记录!✨前言计算机硬件有两种存储数据的方式:大端字节序——Big Endian小端字节序——Little …...

软件测试备战近三银四--面试心得
自信即巅峰,对待面试官就像和儿子一样,耐心!耐心!耐心!...
《Linux运维实战:ansible中的变量定义及以及变量的优先级》
一、配置文件优先级 Ansible配置以ini格式存储配置数据,在Ansible中⼏乎所有配置都可以通过Ansible的Playbook或环境变量来重新赋值。在运⾏Ansible命令时,命令将会按照以下顺序查找配置⽂件。 # ⾸先,Ansible命令会检查环境变量,…...
 监听 Form表单变化)
useEffect 通过 form.getFieldValue(‘xxx‘) 监听 Form表单变化
场景 子组件中,某一个表格的数据需要依赖于上级组件的某一个表单元素值进行计算。 毫无疑问,首先想到的肯定是监听 form 表单中元素的值,使用 useEffect 监听表单的变化,当值发生变化时,重新计算渲染。 首先说下我的…...
【晓龙oba出品 - 黑科技解题系列】- 最小操作次数使数组元素相等
思路 算法归根到底就是找规律的游戏,我们首先来看一个现象: 以数组nums [1,2,3,4,5]为例 当我们将数组排序后,可以知道最小值为1,最大值为5,此时我们需要四次运算可以使最小值与最大值相等: 第一次:2,3,4,…...
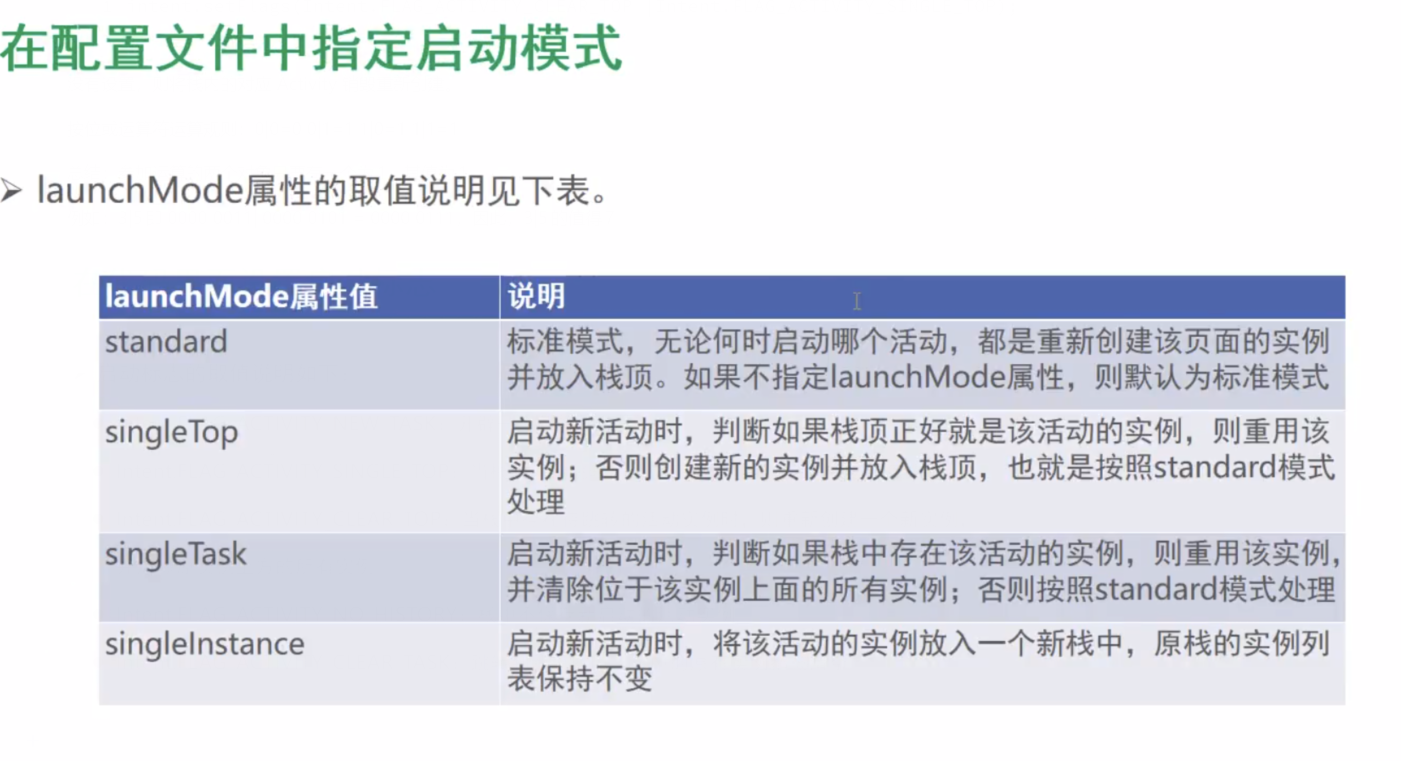
Activity的启动和结束
onCreate:创建活动。此时会把页面布局加载进内存,进入了初始状态。onStart:开启活动。此时会把活动页面显示在屏幕上,进入了就绪状态。onResume:恢复活动。此时活动页面进入活跃状态,能够与用户正常交互&am…...

利用业务逻辑+OB分布式特性优化SQL
最近某人社局核心数据库上了OB,经常出现性能问题 某人社与我司合作多年,非常信任我司在数据库的专业能力,邀请我司过去看看能否提供帮助 与OB驻场工程师合作,抓取了一天的TOP SQL,跑得慢的SQL有几十条(注意只是某一天的…...

哈希表
文章目录什么是哈希问题引入哈希函数直接定址法除留余数法 (常用、重点)哈希冲突哈希冲突的解决方法闭散列开散列unordered_map && unordered_set 封装实现哈希的应用位图布隆过滤器哈希经典面试题哈希切分位图应用布隆过滤器什么是哈希 在上一…...
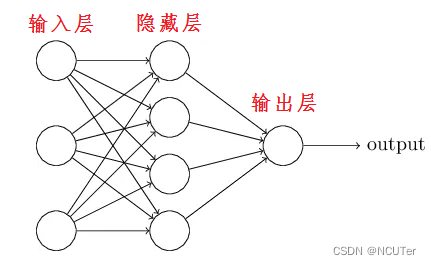
基于Halcon的MLP(多层感知神经网络)分类器分类操作实例
一、介绍 人工神经网络(Artificial Neural Network,ANN)简称神经网络(Neural Network,NN)或类神经网络,是一种模仿生物神经网络的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。 MLP神经网络是一种基于神经网络、动态的分类器。MLP分类器使用神经…...
VR全景博物馆,打造7*24小时的线上参访体验
导语:博物馆作为人们了解历史、文化和艺术的重要场所,现在可以通过VR全景技术来进行展览,让参观者身临其境地感受历史文化的魅力。本文将介绍博物馆VR全景的特点、优势,以及如何使用VR全景技术来丰富博物馆的展览和教育活动。什么…...

Go 数据类型
基础数据类型 类型长度(字节)默认值说明bool1falsebyte10uint8,取值范围[0,255]rune40Unicode Code Point,int32int,uint4或者8032位或64位操作系统int8,uint810-128~127,0-255int16,uint1620-32768~32767,…...
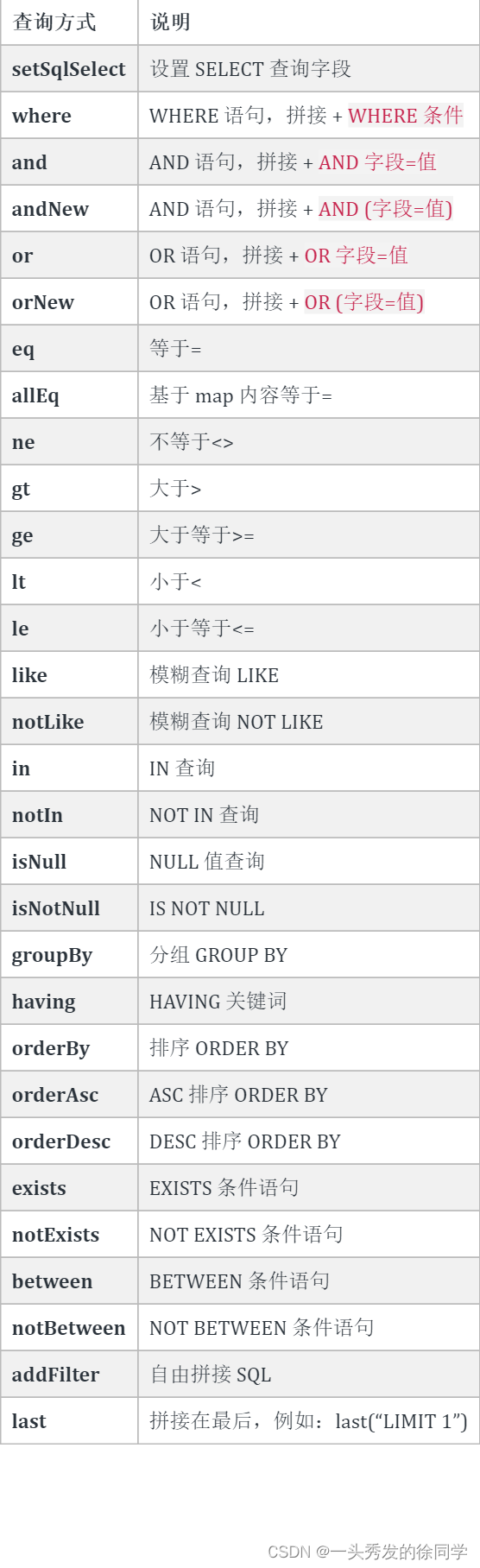
Mybatis-Plus学透?一篇足够(持续更新中)
01、Mybatis-Plus入门 一、简介 MyBatis-Plus(简称 MP)是一个 MyBatis 的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。如果你想对自己的项目进行技术升级,不妨尝试将mybatis换成Mybati…...

船用燃料油市场调研报告-主要企业、市场规模、份额及发展趋势
船用燃料油市场报告主要研究:市场规模: 产能、产量、销售、产值、价格、成本、利润等行业分析:原材料、市场应用、产品种类、市场需求、市场供给,下游市场分析、供应链分析等竞争分析:主要企业情况、市场份额、并购、扩…...
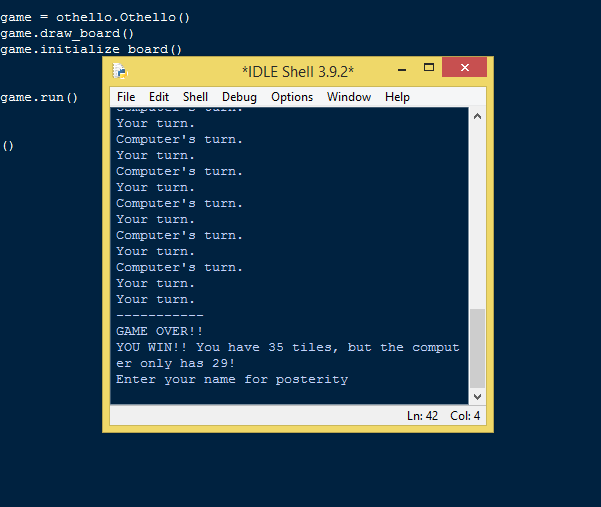
python趣味编程-奥赛罗游戏
在上一期我们用Python实现了一个高速公路汽车游戏的游戏,这一期我们继续使用Python实现一个简单的奥赛罗游戏,让我们开始今天的旅程吧~ 在Python中使用Turtle实现的奥赛罗游戏 在Python中使用Turtle的简单奥赛罗游戏 是一个以 Python 为程序设计语言的项…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
