【最优化方法】实验三 无约束最优化方法的MATLAB实现
实验的目的和要求:通过本次实验使学生进一步熟悉掌握使用MATLAB软件,并能利用该软件进行无约束最优化方法的计算。
实验内容:
1、最速下降法的MATLAB实现
2、牛顿法的MATLAB实现
3、共轭梯度法的MATLAB实现
学习建议:
本次实验就是要通过对一些具体问题的分析进一步熟悉软件的操作并加深对理论知识的理解。
重点和难点:
通过同一个具体问题用不同的方法解决的比较,加深理解恰当选用优化问题解决方法的重要性。
一 最速下降法
1.最速下降法基本原理和步骤
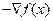 思想:寻求最速下降方向即负梯度方向
思想:寻求最速下降方向即负梯度方向

MATLAB实现:
2.代码及数值算例:
(1) 程序源代码:
function [ X,FMIN,K ] = zuisuxiajiang( f,x,x0,e )% [ X,FMIN,N ] =zuisuxiajiang()法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15 count=0;td=jacobian(f,x)';while norm(subs(td,x,x0))>eP=-subs(td,x,x0);syms ry=x0+r*P;ft(r)=subs(f,x,y); [r0]=fibonacci(ft,0,100,0.01);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
二 牛顿法
1.牛顿法基本原理和步骤
思想:在第k次迭代的迭代点x(k)邻域内,用一个二次函数(如二阶泰勒多项式)去近似代替原目标函数f(x),然后求出该二次函数的极小点作为对原目标函数求优的下一个迭代点,依次类推,通过多次重复迭代,使迭代点逐步逼近原目标函数的极小点。
设*f(x)*二次连续可微,在点 x(k) 处的Hesse矩阵正定。

MATLAB实现:
2.代码及数值算例:
(2) 程序源代码:
function [ X,FMIN,K ] = ysNewton( f,x,x0,e )% [ X,FMIN,N ] =ysNewton()原始牛顿法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15count=0;td=jacobian(f,x)';H=jacobian(td',x);while norm(subs(td,x,x0))>eP=-subs(H,x,x0)^(-1)*subs(td,x,x0);x0=x0+P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
牛顿法对于二次正定函数只需做一次迭代就得到最优解。特别在极小点附近,收敛性很好速度也很快。
但牛顿法也有缺点,它要求初始点离最优解不远,若初始点选的离最优解太远时,牛顿法并不能保证其收敛,甚至也不是下降方向。
为了克服牛顿法的缺点,人们保留了从牛顿法中选取牛顿方向作为搜索方向,摒弃其步长恒取1的作法,而用一维搜索确定最优步长来构造算法。

(3) 程序源代码:
function [ X,FMIN,K ] = xzNewton( f,x,x0,e )% [ X,FMIN,N ] =xzNewton()带步长牛顿法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15count=0;td=jacobian(f,x)';H=jacobian(td',x);while norm(subs(td,x,x0))>eP=-subs(H,x,x0)^(-1)*subs(td,x,x0);syms ry=x0+r*P;ft(r)=subs(f,x,y); [r0]=fibonacci(ft,0,100,0.01);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
三 共轭梯度法
1.共轭梯度法基本原理和步骤
思想:将共轭性和最速下降方向相结合,利用已知迭代点处的梯度方向构造一组共轭方向,并沿此方向进行搜索,求出函数的极小点。

MATLAB实现:
2.代码及数值算例:
(1) 程序源代码:
function [ X,FMIN,K ] = gongetidu( f,x,x0,e )% [ X,FMIN,N ] =gongetidu()共轭梯度法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15count=1;td=jacobian(f,x)';H=jacobian(td',x);if norm(subs(td,x,x0))>eP=-subs(td,x,x0);r0=-subs(td,x,x0)'*P/(P'*H*P);x0=x0+r0*P;else x0;endwhile norm(double(subs(td,x,x0)))>eb0=subs(td,x,x0)'*subs(td,x,x0)/(P'*P);P=-subs(td,x,x0)+b0*P;r0=-subs(td,x,x0)'*P/(P'*H*P);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
四 一个算例
分别用上述三中方法计算下题,并比较各算法.
Min f(x)=(x1 - 2)^2 + (x1 – 2*x2)^2
初始点x0=(0,3)T
允许误差e=0.1
键入命令并输出结果:
syms x1 x2\>> f=(x1-2)^2+(x1-2*x2)^2;\>> x=[x1;x2];\>> x0=[0;3];\>> e=0.1;[X,FMIN,N]=zuisuxiajiang(f,x,x0,e)X =1.97630.9818FMIN =7.2076e-04N =10\>> [X,FMIN,N]=ysNewton(f,x,x0,e)X =21FMIN =0N =1[X,FMIN,N]=gongetidu(f,x,x0,e)X =21FMIN =0N =2
由上述结果我们发现:
对于二次正定函数newton法只需一次迭代就得到正确结果,共轭梯度法只需进行两次(因为目标函数是二元函数)迭代就得出正确结果。但最速下降法却迭代了10次,虽然一维搜索存在误差,但实际上最速下降法也需迭代多次。
相关文章:

【最优化方法】实验三 无约束最优化方法的MATLAB实现
实验的目的和要求:通过本次实验使学生进一步熟悉掌握使用MATLAB软件,并能利用该软件进行无约束最优化方法的计算。 实验内容: 1、最速下降法的MATLAB实现 2、牛顿法的MATLAB实现 3、共轭梯度法的MATLAB…...
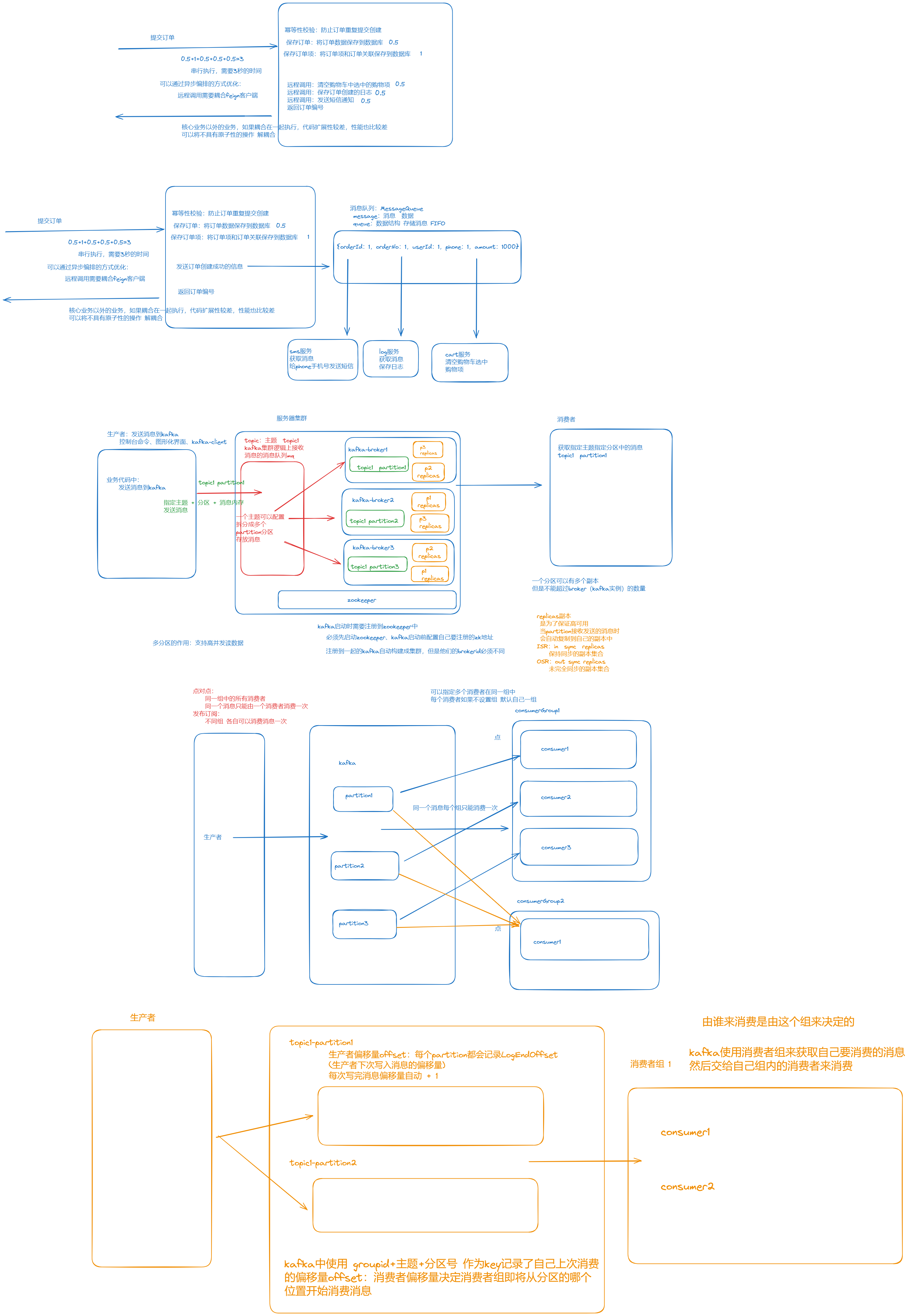
kafka-偏移量图解
生产者偏移量:生产者发送消息时写入到哪个位置(主题的每个分区会存储一个 leo 即将写入消息的偏移量),每次写完消息 leo 会 1 消费者偏移量:消费者从哪个位置开始消费消息,小于等于 leo,每个组…...
内网安全--隧道技术-MSF上线本地
免责声明:本文仅做技术交流与学习... 不得不说,小白最近也是用上了viper,这里要特别感谢一下my bro 北岭敲键盘的荒漠猫 MSF--viper: --生成马子-->上线 --进入meterpreter. 1-查看路由,添加路由. 查看路由信息 : run autoroute -p run post/multi/manage/autoroute 添加…...
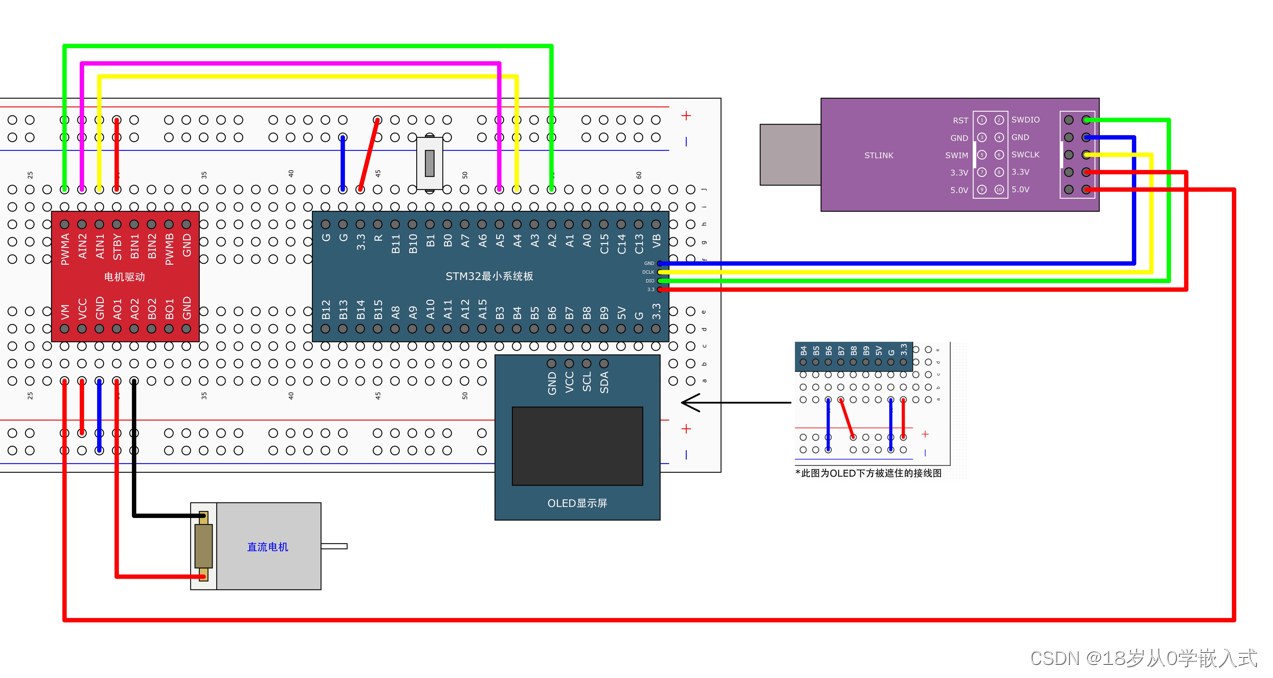
初识STM32单片机-TIM定时器
初识STM32单片机-TIM定时器 一、定时器概述二、定时器类型2.1 基本定时器(TIM6和TIM7)2.2 通用定时器(TIM2、TIM3、TIM4和TIM5)2.3 高级定时器(TIM1和TIM8) 三、定时中断基本结构和时基单元工作时序3.1 定时器基本结构3.2 预分频器时序3.3 计数器时序3.3.1 计数器有无预装时序(…...
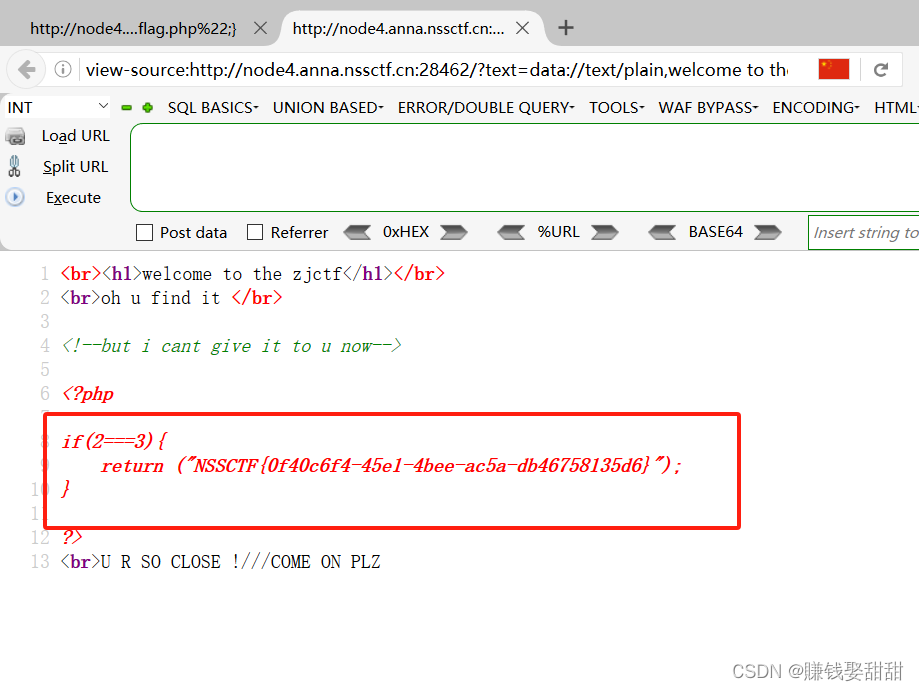
NSSCTF-Web题目3
目录 [BJDCTF 2020]easy_md5 1、知识点 2、题目 3、思路 [ZJCTF 2019]NiZhuanSiWei 1、知识点 2、题目 3、思路 第一层 第二层 第三层 [BJDCTF 2020]easy_md5 1、知识点 弱比较,强比较、数组绕过、MD5加密 2、题目 3、思路 1、首先我们跟着题目输入&a…...
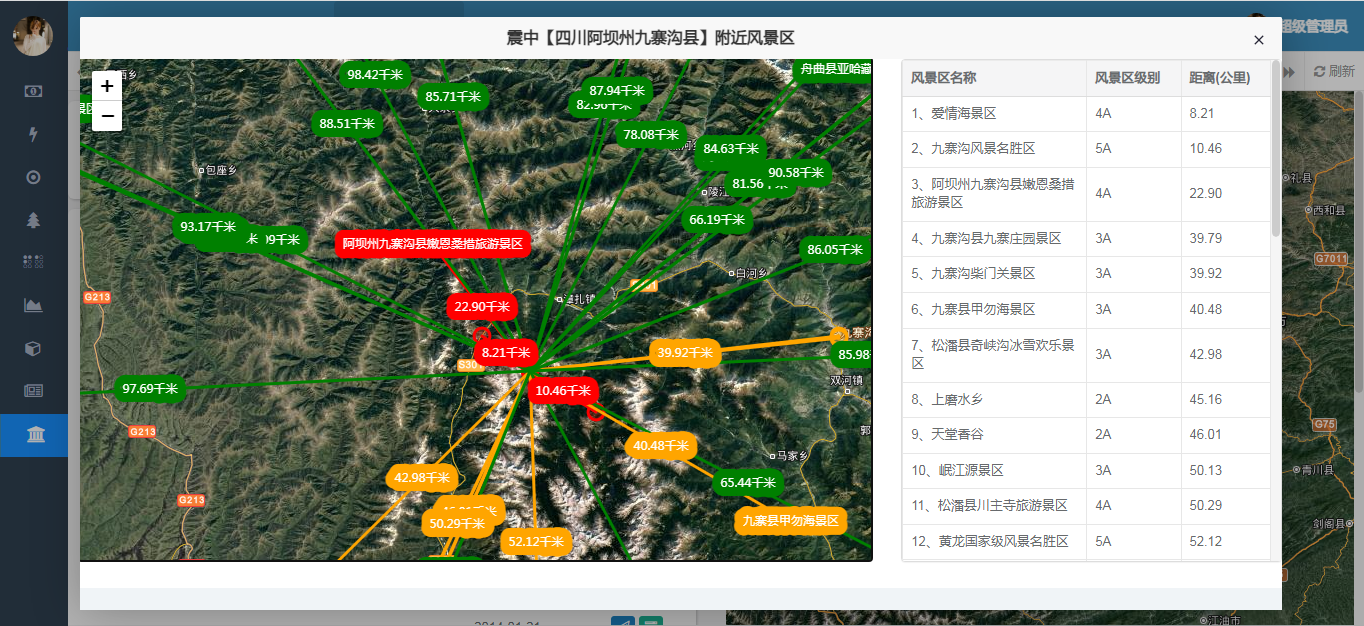
基于Java实现震中附近风景区预警可视化分析实践
目录 前言 一、空间数据说明 1、表结构信息展示 2、空间范围查询 二、Java后台开发实现 1、模型层设计与实现 2、控制层设计与实现 三、Leaflet地图开发 1、地震震中位置展示 2、百公里风景区列表展示 3、风景区列表展示 4、附近风景区展示 四、总结 前言 地震这类…...

【CTF Web】CTFShow web7 Writeup(SQL注入+PHP+进制转换)
web7 1 阿呆得到最高指示,如果还出问题,就卷铺盖滚蛋,阿呆心在流血。 解法 注意到: <!-- flag in id 1000 -->拦截很多种字符,连 select 也不给用了。 if(preg_match("/\|\"|or|\||\-|\\\|\/|\\*|\…...

ABAP WRITE换行输出
不换行: write hello world!. write 春天马上就到了!. 换行: write hello world!. write /春天马上就到了!. 换行的第二种: write: hello world! ,/,春天马上就到了!....
VUE3学习第一篇:启动ruoyi
1、找到ruoyi的vue3版本 然后下载代码到本地, 我刚开始用的nodejs14报错, 后面换成nodejs16,启动前端成功了。 页面如下图所示...
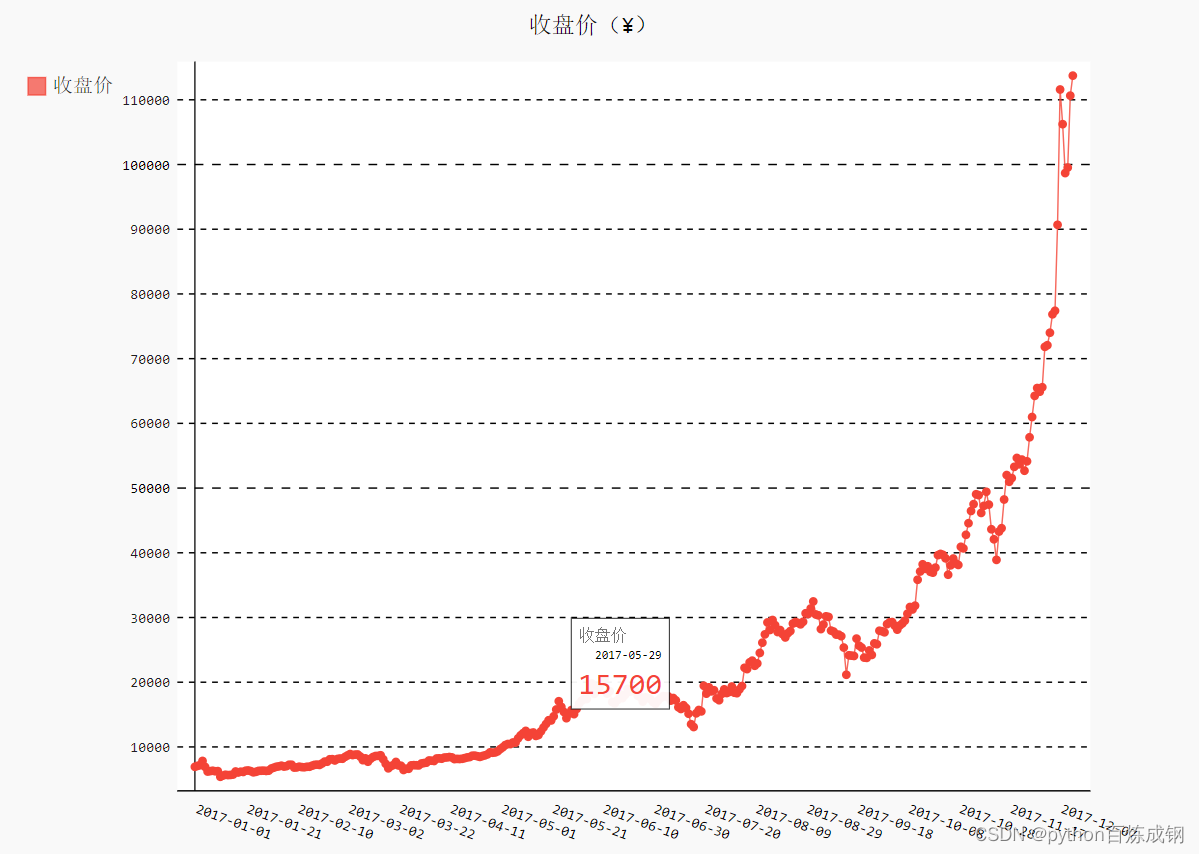
python-数据可视化(总)
python-数据可视化 ** 数据可视化 指的是通过可视化表示来探索数据,它与数据挖掘**紧密相关,而数据挖掘指的是使用代码来探索数据集的规律和关联。数据集可以是用一行代码就能表示的小型数字列表,也可以是数以吉字节的数据 最流行的工具之一…...
使用git生成SSH公钥,并设置SSH公钥
1、在git命令行里输入以下命令 ssh-keygen -t rsa 2、按回车,然后会看到以下字眼 Generating public/private rsa key pair. Enter file in which to save the key (/c/Users/xxx/.ssh/id_rsa) 例: 3、继续回车,然后会看到以下字眼 Enter…...

iPhone win10更改备份路径
1 删掉或改名 旧的Backup, 否则不能连接 ren "C:\Users\Administrator\Apple\MobileSync\Backup" Backup_old 2 在目标盘中 创建新的文件夹 手动创建 MobileSync\Backup 3 链接两个文件夹 mklink /J "C:\Users\Administrator\Apple\MobileSync\Backup" &qu…...

Jmeter元件及基本作用域
🚀从今天开始学习性能测试工具——Jmeter,小梦也是先学习了下Jmeter的元件概念以及其基本的作用域,整理了下笔记,希望不管是从事开发领域还是测试领域的朋友们,我们一起学习下Jmeter工具,提升工作中的技能&…...

GB-T 43696-2024 网络安全技术 零信任参考体系架构
GB-T 43696-2024 网络安全技术 零信任参考体系架构 编写背景 随着网络环境的日益复杂,传统的网络安全策略已经难以满足现代企业的需求。为了应对不断变化的安全威胁,零信任安全模型应运而生。GB-T 43696-2024《网络安全技术 零信任参考体系架构》是中国…...

Java使用apache.poi生成excel插入word中
加油,新时代打工人! 工作需求,上个文章我们生成好的word,这次将生成好的excel表格数据,插入word中。需要准备好excle数据,然后插入到word中。 最后个需要,就是把这些生成好的word文档转成pdf进行…...

斯坦福报告解读3:图解有趣的评估基准(上)
《人工智能指数报告》由斯坦福大学、AI指数指导委员会及业内众多大佬Raymond Perrault、Erik Brynjolfsson 、James Manyika等人员和组织合著,旨在追踪、整理、提炼并可视化与人工智能(AI)相关各类数据,该报告已被大多数媒体及机构…...

C语言---扫雷游戏的实现
1.扫雷游戏的分析和设计 需要创建3个文件夹 test.c----扫雷游戏的测试 game.c----扫雷游戏的实现 game.h----扫雷游戏的实现 雷的信息使用二维数组存放 • 使⽤控制台实现经典的扫雷游戏 • 游戏可以通过菜单实现继续玩或者退出游戏 • 扫雷的棋盘是9*9的格⼦ • 默认…...
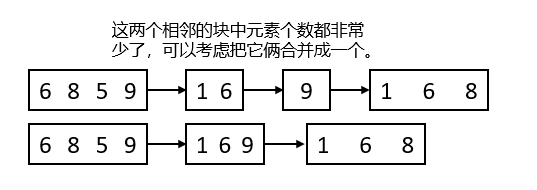
《征服数据结构》块状链表
摘要: 1,块状链表的介绍 2,块状链表的代码实现(Java和C) 1,块状链表的介绍 前面我们讲过数组和链表,数组具有 O(1)的查询时间,O(N)的删除,O(N)的插入,而链表具…...

leetCode.86. 分隔链表
leetCode.86. 分隔链表 题目思路: 代码 class Solution { public:ListNode* partition(ListNode* head, int x) {auto lh new ListNode(-1), rh new ListNode(-1);auto lt lh, rt rh;for(auto p head; p; p p->next ) {if(p->val < x) {lt lt->…...
Java进阶学习笔记5——Static应用知识:单例设计模式
设计模式: 架构师会使用到设计模式,开发框架,就需要掌握很多设计模式。 在Java基础阶段学习设计模式,将来面试笔试的时候,笔试题目会经常靠到设计模式。 将来会用到设计模式。框架代码中会用到设计模式。 什么是设计…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
