leetcode力扣 300. 最长递增子序列 II
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
1 <= nums.length <= 2500
-1e4 <= nums[i] <= 1e4
进阶思考:
你能将算法的时间复杂度降低到 O(n log(n)) 吗?
题解:
一共有两种写法: 第一种的时间复杂度是O(n ^ 2), 第二种的时间复杂度是O(n * logn)
第一种写法:
动态规划的题
f[i]: 只考虑前 i 个数(包含i), 并且以第i个数结尾的子序列的所有方案的子序列长度的最大值
状态表示:
- 集合: 只考虑前 i 个数(包含i), 并且以第i个数结尾的子序列的所有方案
- 属性: 子序列长度的最大值
状态计算:
对于第 i 个数的状态转移方程是:
- 只有一个第 i 个数, 此时f[i] = 1;
- 以第1个数结尾的基础上再选第i个数尾结尾, 以第2个数结尾的基础上再选第i个数结尾…以第i - 1个数结尾的基础上再选第i个数结尾,上面所有情况的长度取max就是f[i], 也就是 f[j] + 1, 因为选第i个数, 所有长度加1, j 属于(0, i)
看不懂状态计算的话, 一定要多理解状态表示, 理解了状态表示, 就可以理解状态计算
ac代码👇 时间复杂度(O(n ^ 2))
class Solution {
public:int lengthOfLIS(vector<int>& nums) {if (nums.size() == 0) return 0;// 以第i个数结尾的最长上升子序列 maxvector<int> f(nums.size(), 0);for (int i = 0; i < nums.size(); i ++){f[i] = 1; // 只有第i个数的情况, 也就是状态计算1for (int j = 0; j < i; j ++) // 状态计算2if (nums[i] > nums[j]) f[i] = max(f[i], f[j] + 1); // 要加上判断, 使子序列满足严格的单调递增}int res = 0; // 最长上升子序列不一定会选最后一个, 也不一定会选倒数第二个..., 所有最后的答案是f数组中的最大值, 主要还是要理解状态表示for (int i = 0; i < f.size(); i ++) res = max(res, f[i]);return res;}
};
第二种写法
贪心 + 二分
子序列长度要想尽可能大, 在相同长度的情况下, 我们要让子序列末尾的元素尽可能小, 这样后面进来的元素才能尽可能地多,所以我们维护一个数组 f[i]: 长度为 i 的最长上升子序列末尾的最小值。
对于每个nums[i], 有两种情况
- 如果nums[i] 比 f[len] 大的话, 直接让 f 的长度 + 1, 然后f[len + 1] 的值是nums[i]
- 如果nums[i] 比 f[len] 小的话, 需要从f数组中找到 第一个大于等于 nums[i] 的位置, 并把这个值重新赋值为nums[i]
其实上面的过程更像是我们人来找最长上升子序列的时候的样子
为了让大家更好理解, 这里模拟下下面的一个样例
输入样例: 1 2 3 8 4 5 6 7d[1] = nums[0] = 1; (初始化)
循环次数 i d的值 len 长度1 d[2] = 2; 22 d[3] = 3; 33 d[4] = 8; 4 4 d[4] = 4 4 因为4比8小, 通过二分查找到8的位置, 8在d数组中的下标是4, 所以d[4]的值应该被修改成45 d[5] = 5 56 d[6] = 6 67 d[7] = 7 7
ac 代码👇 时间复杂度O(n * logn)
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();if (n == 0) return 0;vector<int> f(n + 1, 0); // f下标从1开始int len = 1; f[len] = nums[0];for (int i = 1; i < n; i ++){if (nums[i] > f[len]) f[++ len] = nums[i];else{int l = 1, r = len;while (l < r) // 查找第一个大于等于nums[i]{int mid = l + r >> 1; // 右移一位, 相当于(l + r) / 2if (f[mid] < nums[i]) l = mid + 1;else if(f[mid] >= nums[i]) r = mid;}f[l] = nums[i];}}return len;}
};
对于二分的退出条件的差异:
while(l < r)和while (l <= r)
while(l < r) 对应的代码, 退出的时候 l == r
int l = 0, r = len;
while (l < r){int mid = l + r >> 1;if (f[mid] < nums[i]) l = mid + 1;else if(f[mid] >= nums[i]) r = mid;}
while (l <= r)对应的代码, 退出的时候 l > r
int l = 0, r = len;
while (l <= r){int mid = l + r >> 1;if (f[mid] < nums[i]) l = mid + 1;else if(f[mid] >= nums[i]) r = mid - 1;}
上面两个代码找到的都是第一个大于等于nums[i]的下标, 但while循环里面略有不同
个人习惯用while(l < r), 感觉这种方法里面l和r的边界好理解
if (f[mid] < nums[i]) l = mid + 1; 说明 mid 位置上的数不满足 f[mid] < nums[i], 所有要到二分的右边去找,并且不包过 mid这个位置的数
else if(f[mid] >= nums[i]) r = mid; 说明 mid 位置上的数可能满足 f[mid] < nums[i], 所以要到二分的左边去找, 并且包含mid这个位置上的数
觉得写的不错的话, 点个赞吧~
相关文章:

leetcode力扣 300. 最长递增子序列 II
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 示例 1&#…...

C++_vector简单源码剖析:vector模拟实现
文章目录 🚀1.迭代器🚀2.构造函数与析构函数⚡️2.1 默认构造函数vector()⚡️2.2 vector(int n, const T& value T())⚡️内置类型也有构造函数 ⚡️2.3 赋值重载operator⚡️2.4 通用迭代器拷贝⚡️2.5 vector(initializer_list<T> il)⚡️…...

第3章 数据链路层
王道学习 考纲内容 (一)数据链路层的功能 (二)组帧 (三)差错控制 检错编码;纠错编码 (四)流量控制与可靠传输机制 流量控制、可靠传输与滑动窗口…...

使用OrangePi KunPeng Pro部署AI模型
目录 一、OrangePi Kunpeng Pro简介二、环境搭建三、模型运行环境搭建(1)下载Ollama用于启动并运行大型语言模型(2)配置ollama系统服务(3)启动ollama服务(4)启动ollama(5)查看ollama运行状态四、模型部署(1)部署1.8b的qwen(2)部署2b的gemma(3)部署3.8的phi3(4)部署4b的qwen(5)部…...

SpringMVC 数据映射VC
从 view 层发送请求到Controller,在Controller中获取参数: 在不输入值时会报400,参数错误 在不输入值时num默认为null 没有找到对应标签名称叫nums的,输入任何值时都报400 设置required默认值为false,即使表单没有nums…...
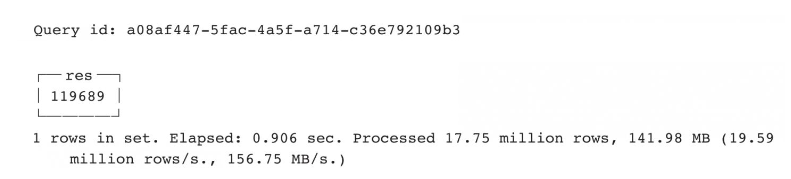
Clickhouse Bitmap 类型操作总结—— Clickhouse 基础篇(四)
文章目录 创建 Bitmap 对象Bitmap 转换为整数数组计算总数(去重)值指定start, end 索引生成子 Bitmap指定 start 索引和数量限制生成子 Bitmap指定偏移量生成子 Bitmap是否包含指定元素两个 Bitmap 是否存在相同元素一个是否为另一个 Bitmap 的子集求最小…...

202474读书笔记|《我自我的田渠归来》——愿你拥有向上的力量,一切的好事都应该有权利发生
202474读书笔记|《我自我的田渠归来》——愿你拥有向上的力量 《我自我的田渠归来》作者张晓风,被称为华语散文温柔的一支笔,她的短文很有味道,角度奇特,温柔慈悲而敏锐。 很幸运遇到了这本书,以她的感受重新认识一些事…...
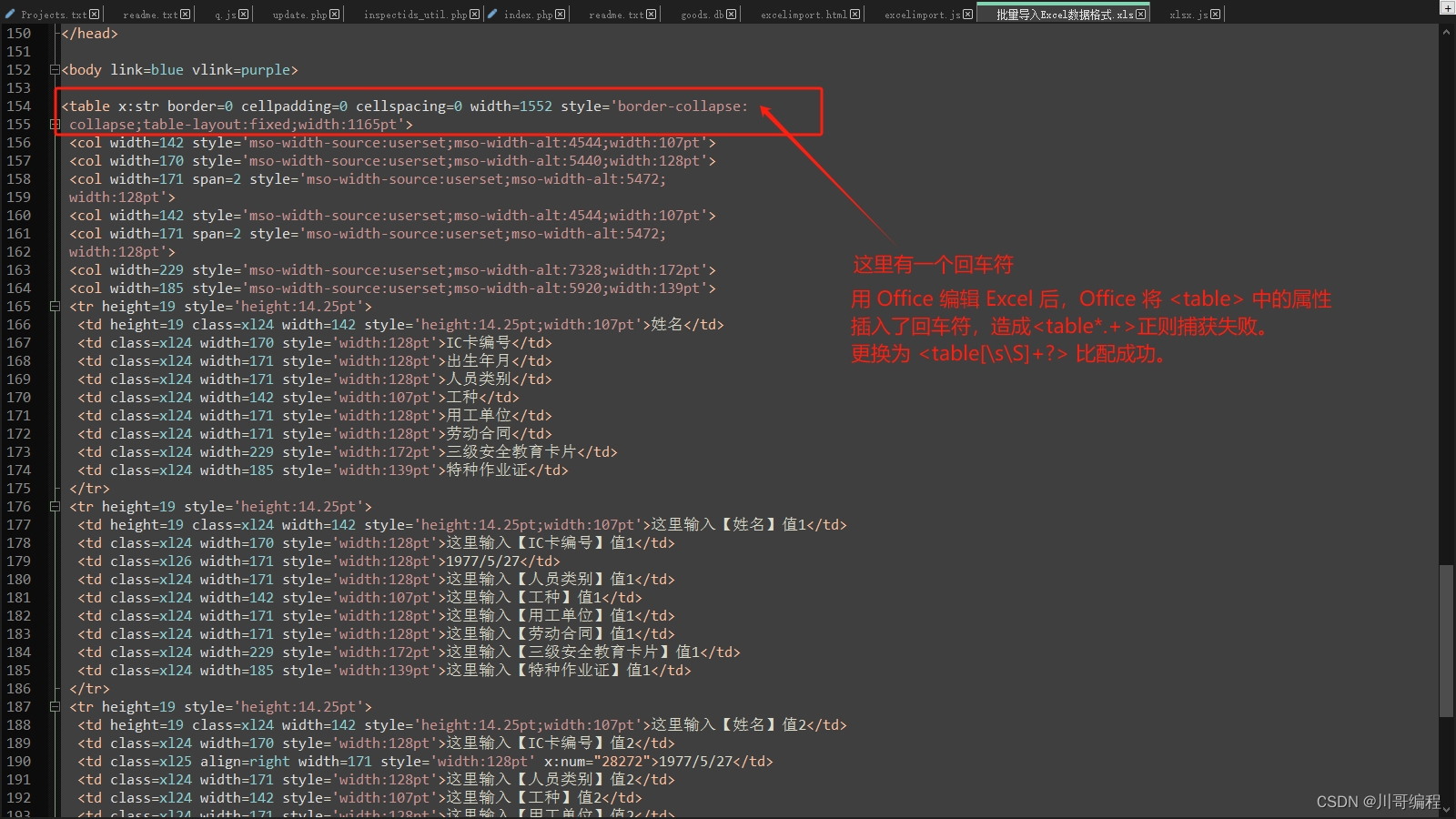
SheetJS V0.17.5 导入 Excel 异常修复 Invalid HTML:could not find<table>
导入 Excel 提示错误:Invalid HTML:could not find<table> 检查源代码 发现 table 属性有回车符 Overview: https://docs.sheetjs.com/docs/ Source: https://git.sheetjs.com/sheetjs/sheetjs/issues The public-facing websites of SheetJS: sheetjs.com…...
重学java51.Collections集合工具类、泛型
"我已不在地坛,地坛在我" —— 《想念地坛》 24.5.28 一、Collections集合工具类 1.概述:集合工具类 2.特点: a.构造私有 b.方法都是静态的 3.使用:类名直接调用 4.方法: static <T> boolean addAll(collection<? super T>c,T... el…...
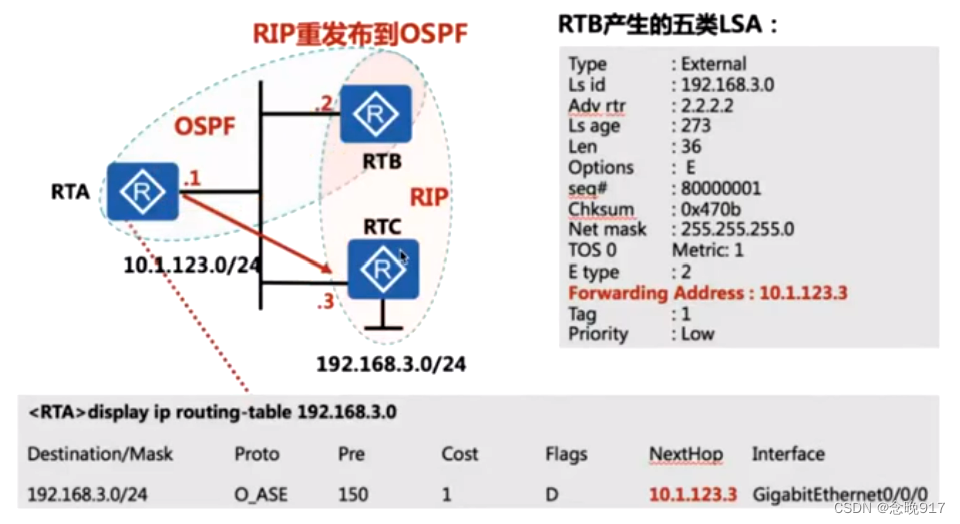
OSPF扩展知识2
FA-转发地址 正常 OSPF 区域收到的 5 类 LSA 不存在 FA 值; 产生 FA 的条件: 1、5类LSA ----假设 R2为 ASBR,90/0 口工作的 OSPF 中,g0/1 口工作在非 ospf 协议或不同 ospf 进程中;若 g0/1 也同时宣告在和 g0/0 相同的 OSPF 进程…...

数据库技术基础
数据库技术基础 导航 文章目录 数据库技术基础导航一、基础概念数据库系统数据库管理系统DBMS分类数据库技术的发展数据库体系结构 二、数据模型数据模型基本概念 三、数据库的控制功能事务概述SOL中事务定义语句日志文件故障种类两个操作Undo/Redo事务故障的恢复系统故障的恢…...

这些项目,我当初但凡参与一个,现在也不至于还是个程序员
10年前,我刚开始干开发不久,我觉得这真是一个有前景的职业,我觉得我的未来会无限广阔,我觉得再过几年,我一定工资不菲。于是我开始像很多大佬说的那样,开始制定职业规划,并且坚决执行。但过去这…...

ch2应用层--计算机网络期末复习
2.1应用层协议原理 网络应用程序位于应用层 开发网络应用程序: 写出能够在不同的端系统上通过网络彼此通信的程序 2.1.1网络应用程序体系结构分类: 客户机/服务器结构 服务器: 总是打开(always-on)具有固定的、众所周知的IP地址 主机群集常被用于创建强大的虚拟服务器 客…...

Red Hat Enterprise Linux (RHEL) 8.10 发布 - 红帽企业 Linux 8 完美终结版
Red Hat Enterprise Linux (RHEL) 8.10 (x86_64, aarch64) - 红帽企业 Linux 红帽企业 Linux 8 完美终结版 请访问原文链接:Red Hat Enterprise Linux (RHEL) 8.10 (x86_64, aarch64) - 红帽企业 Linux,查看最新版。原创作品,转载请保留出处…...
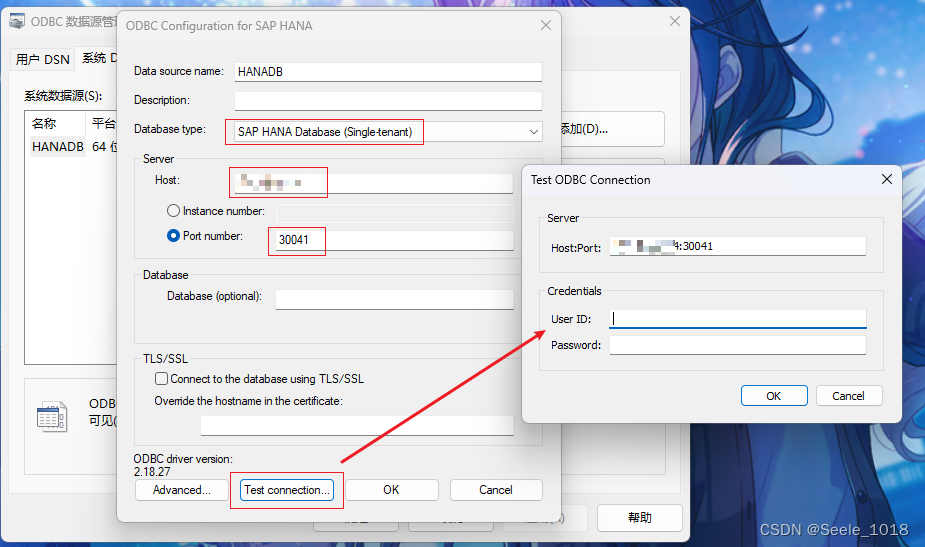
.NET 直连SAP HANA数据库
前言 上个项目碰到的需求,IT部门要求直连SAP的HANA数据库,以只读的权限读取SAP部门开发的CDS视图,是个有点复杂的工程,需要从成品一直往前追溯到原材料的产地,和交货单、工单、采购订单有相当程度上的关联 IT部门要求…...

HTML <from>表单
定义:<form>元素定义了一个表单,用户可以在表单中输入数据,这些数据可以被提交到服务器。 属性: action:指定表单提交时的目标URL(服务器端脚本的地址)。 method:定义提交表…...
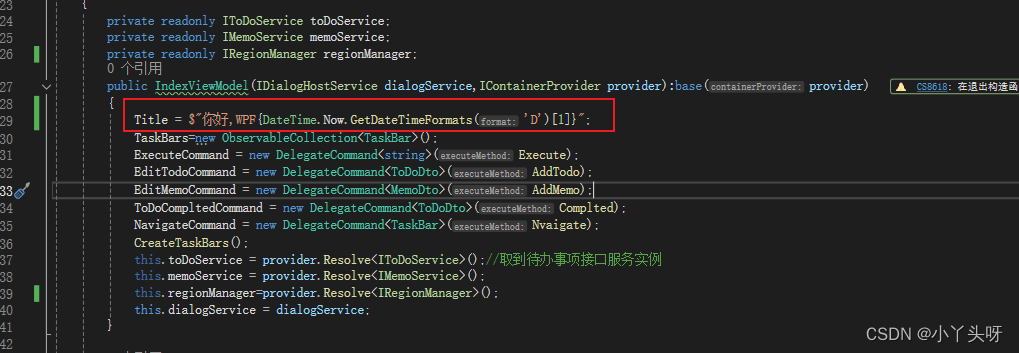
Wpf 使用 Prism 实战开发Day28
首页汇总方块点击导航功能 点击首页汇总方块的时候,跳转到对应的数据页面 step1: 在IndexViewModel 中,给TaskBar 里面Target 属性,赋上要跳转的页面 step2: 创建导航事件命令和方法实现 step3: 实现导航的逻辑。通过取到 IRegionManager 的…...

如何让一个普通用户可以读写某个目录
循环设置这个目录以及上面每一级目录的读取和执行权限 sudo chmod -R orx /opt/software/yourdir 然后设置指定用户user1可以读写这个目录 sudo setfacl -Rm u:user1:rwx /opt/software/yourdir 读取acl sudo getfacl -R /opt/software/yourdir -R 是循环读取子目录和文件的意思…...

知识笔记——jieba分词初探
1. 简介 jieba 是python中一个非常好用的 中文分词组件,但它并不是只有分词这一个功能,还提供了很多在分词之上的算法,如关键词提取、词性标注等。 安装方式: pip install jieba2. 分词 支持 3 种分词模式:精确模式…...

GPT-4o:人工智能新纪元的开端
引言 近年来,人工智能领域的发展日新月异,特别是在自然语言处理(NLP)领域,各种生成预训练模型不断推陈出新。自OpenAI发布GPT-3以来,生成预训练模型在文本生成、语言理解等任务中展现了强大的能力。近期&a…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

[特殊字符] Spring Boot底层原理深度解析与高级面试题精析
一、Spring Boot底层原理详解 Spring Boot的核心设计哲学是约定优于配置和自动装配,通过简化传统Spring应用的初始化和配置流程,显著提升开发效率。其底层原理可拆解为以下核心机制: 自动装配(Auto-Configuration) 核…...
