Educational Codeforces Round 127 D. Insert a Progression
Insert a Progression
You are given a sequence of n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an. You are also given x x x integers 1 , 2 , … , x 1, 2, \dots, x 1,2,…,x.
You are asked to insert each of the extra integers into the sequence a a a. Each integer can be inserted at the beginning of the sequence, at the end of the sequence, or between any elements of the sequence.
The score of the resulting sequence a ′ a' a′ is the sum of absolute differences of adjacent elements in it ( ∑ i = 1 n + x − 1 ∣ a i ′ − a i + 1 ′ ∣ ) \left(\sum \limits_{i=1}^{n+x-1} |a'_i - a'_{i+1}|\right) (i=1∑n+x−1∣ai′−ai+1′∣).
What is the smallest possible score of the resulting sequence a ′ a' a′?
Input
The first line contains a single integer t t t ( 1 ≤ t ≤ 1 0 4 1 \le t \le 10^4 1≤t≤104) — the number of testcases.
The first line of each testcase contains two integers n n n and x x x ( 1 ≤ n , x ≤ 2 ⋅ 1 0 5 1 \le n, x \le 2 \cdot 10^5 1≤n,x≤2⋅105) — the length of the sequence and the number of extra integers.
The second line of each testcase contains n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an ( 1 ≤ a i ≤ 2 ⋅ 1 0 5 1 \le a_i \le 2 \cdot 10^5 1≤ai≤2⋅105).
The sum of n n n over all testcases doesn’t exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
Output
For each testcase, print a single integer — the smallest sum of absolute differences of adjacent elements of the sequence after you insert the extra integers into it.
Example
| i n p u t \tt input input |
|---|
| 4 1 5 10 3 8 7 2 10 10 2 6 1 5 7 3 3 9 10 10 1 4 10 1 3 1 2 |
| o u t p u t \tt output output |
| 9 15 31 13 |
Tutorial
由题意易得,对于数组 a a a 中已有的数不能改变,此时差值为 ∑ i = 1 ∣ a ∣ a b s ( a i − a i − 1 ) \sum_{i = 1}^{|a|}abs(a_i - a_{i - 1}) ∑i=1∣a∣abs(ai−ai−1),其中 ∣ a ∣ |a| ∣a∣ 表示数组 a a a 的长度
在任意两个数 a i a_i ai 和 a i + 1 a_{i + 1} ai+1 之间,满足 a i ≤ x ≤ a i + 1 a_i \le x \le a_{{i + 1}} ai≤x≤ai+1 条件的 x x x 对答案都不会产生影响,因此插入满足 min ( a ) ≤ x ≤ max ( a ) \min(a) \le x \le \max(a) min(a)≤x≤max(a) 条件的 x x x 均不会对答案产生影响,我们只需要考虑小于 min ( a ) \min(a) min(a) 的数和大于 max ( a ) \max(a) max(a) 的数对答案会产生什么影响即可
对于小于 min ( a ) \min(a) min(a) 的数:
- 如果将 1 , 2 , … , min ( a ) − 1 1,2,\dots,\min(a) - 1 1,2,…,min(a)−1 正序插入到整个数列 a a a 的最前方,产生的影响为 a b s ( a 0 − 1 ) abs(a_0 - 1) abs(a0−1)
- 如果将 min ( a ) − 1 , min ( a ) − 2 , … , 2 , 1 \min(a) - 1, \min(a) - 2, \dots, 2, 1 min(a)−1,min(a)−2,…,2,1 倒序插入到整个数列 a a a 的最后方,产生的影响为 a b s ( a ∣ a ∣ − 1 ) abs(a_{|a|} - 1) abs(a∣a∣−1),其中 ∣ a ∣ |a| ∣a∣ 表示数组 a a a 的长度
- 如果将 1 , 2 , … , min ( a ) − 1 1,2,\dots,\min(a) - 1 1,2,…,min(a)−1 按序插入到数组 a a a 中间,产生的影响为 ( min ( a ) − 1 ) × 2 (\min(a) - 1) \times 2 (min(a)−1)×2
对于大于 max ( a ) \max(a) max(a) 的数:
- 如果将 x − 1 , x − 2 , … , max ( a ) + 1 x - 1, x - 2, \dots, \max(a) + 1 x−1,x−2,…,max(a)+1 倒序插入到整个数列 a a a 的最前方,产生的影响为 a b s ( x − a 0 ) abs(x - a_0) abs(x−a0)
- 如果将 max ( a ) + 1 , max ( a ) + 2 , … , x \max(a) + 1,\max(a) + 2,\dots,x max(a)+1,max(a)+2,…,x 正序插入到整个数列 a a a 的最后方,产生的影响为 a b s ( x − a ∣ a ∣ ) abs(x - a_{|a|}) abs(x−a∣a∣),其中 ∣ a ∣ |a| ∣a∣ 表示数组 a a a 的长度
- 如果将 1 , 2 , … , min ( a ) − 1 1,2,\dots,\min(a) - 1 1,2,…,min(a)−1 按序插入到数组 a a a 中间,产生的影响为 ( x − max ( a ) ) × 2 (x - \max(a)) \times 2 (x−max(a))×2,当然,如果 max ( a ) > x \max(a) > x max(a)>x,此时影响为
0
综上所述,对于每一个数组 a a a 和 x x x,答案为
{ ∑ i = 1 ∣ a ∣ a b s ( a i − a i − 1 ) min ( a b s ( x − a 0 ) , a b s ( x − a ∣ a ∣ ) , max ( 0 , ( x − max ( a ) ) × 2 ) ) min ( a b s ( a 0 − 1 ) , a b s ( a ∣ a ∣ − 1 ) , ( min ( a ) − 1 ) × 2 ) \left\{\begin{matrix} \sum_{i = 1}^{|a|}abs(a_i - a_{i - 1}) \\ \min(abs(x - a_0), abs(x - a_{|a|}), \max(0, (x - \max(a)) \times 2)) \\ \min(abs(a_0 - 1), abs(a_{|a|} - 1), (\min(a) - 1) \times 2) \end{matrix}\right. ⎩ ⎨ ⎧∑i=1∣a∣abs(ai−ai−1)min(abs(x−a0),abs(x−a∣a∣),max(0,(x−max(a))×2))min(abs(a0−1),abs(a∣a∣−1),(min(a)−1)×2)
的和
此解法时间复杂度为 O ( n ) \mathcal O(n) O(n),即求 ∑ i = 1 ∣ a ∣ a b s ( a i − a i − 1 ) \sum_{i = 1}^{|a|}abs(a_i - a_{i - 1}) ∑i=1∣a∣abs(ai−ai−1) 时的时间复杂度
Solution
import sys
input = lambda: sys.stdin.readline().strip()output = []for _ in range(int(input())):n, x = map(int, input().split())a = list(map(int, input().split()))ans = sum(abs(a[i] - a[i + 1]) for i in range(n - 1))mx, mn = max(a), min(a)up = min(abs(x - a[0]), abs(x - a[-1]), (0 if mx > x else (x - mx) * 2))down = min(abs(a[0] - 1), abs(a[-1] - 1), (mn - 1) * 2)output.append(ans + up + down)print('\n'.join(map(str, output)))
相关文章:

Educational Codeforces Round 127 D. Insert a Progression
Insert a Progression time limit per test: 2 second memory limit per test: 256 megabytes input: standard input output: standard output You are given a sequence of n n n integers a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an. You are also giv…...

树莓集团:构筑全国数字影像生态链
在数字化浪潮席卷全球的今天,数字影像技术正以前所未有的速度改变着我们的生活。成都树莓集团以远见卓识和坚定步伐,专注于全国数字影像生态链的建设,不断推动着文创产业的创新与发展。 树莓集团致力于打造一个完整的数字影像生态链ÿ…...
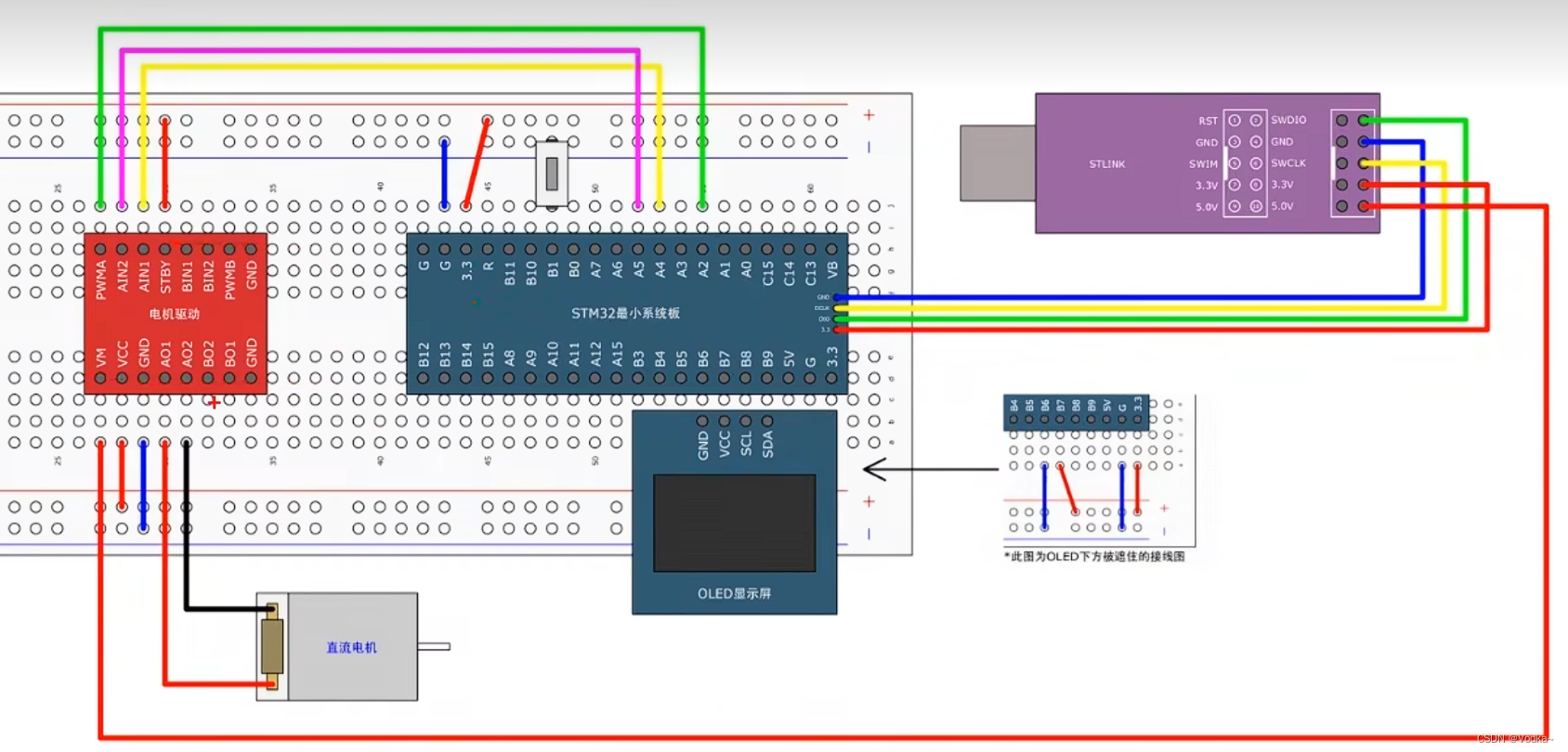
物联网——TIM定时器、PWM驱动呼吸灯、舵机和直流电机
定时器概念(常用于输出PWM波形,驱动电机) 时间脉冲数时钟周期; 这里的脉冲数6553665536,支持定时器级联,从而延长定时 定时器类型 基本定时器原理图(UI:更新中断, U:更新事件&#…...

Elasticsearch 认证模拟题 -2
一、题目 有一个索引 task3,其中有 fielda,fieldb,fieldc,fielde 现要求对 task3 重建索引,重建后的索引新增一个字段 fieldg 其值是fielda,fieldb,fieldc,fielde 的值拼接而成。 …...

Java-----Comparable接口和Comparator接口
在Java中,我们会经常使用到自定义类,那我们如何进行自定义类的比较呢? 1.Comparable接口 普通数据的比较 int a10;int b91;System.out.println(a<b); 那自定义类型可不可以这样比较呢?看一下代码 我们发现会报错,因为自定义…...
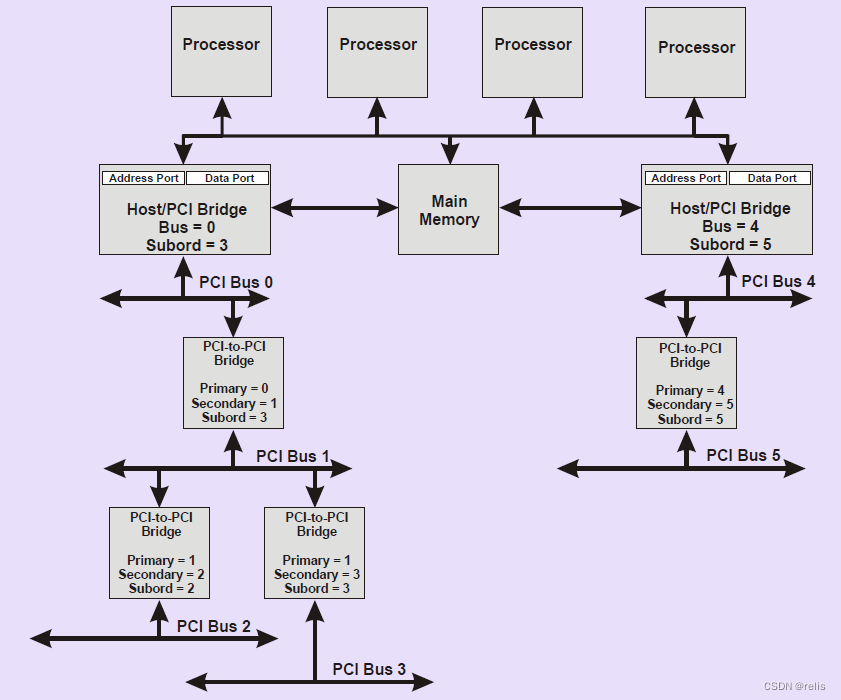
通信技术体会
比如 pcie可以看成是全连接的ahb bus,但又不是。 因为pcie还是axi(神似split/cutthrough)。(axi更多是接口而不是bus)。 pcie虽然物理层和usb都是serdes,但transaction layer就是上面这样的,也就…...

Linux系统安全及其应用
文章目录 一、用户账号安全管理1.1 系统账号的清理1.2 对用户账号的操作1.2.1 锁定和解锁用户1.2.2 删除无用账号 1.3 对重要文件进行锁定1.4 密码安全控制1.4.1 新建用户1.4.2 已有用户 二、历史命令管理2.1 历史命令限制2.2 自动清空历史命令 三、设置终端登录的安全管理3.1 …...
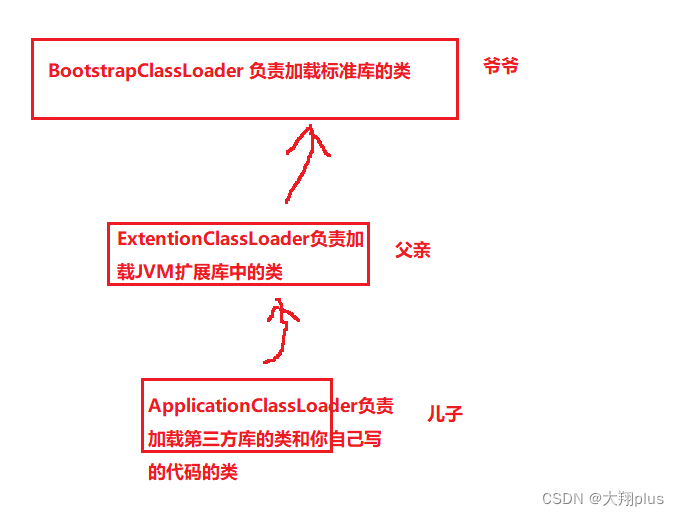
JVM内存划分类加载的过程双亲委派模型的详解
JVM内存划分 JVM也就是java进程,这个进程一旦跑起来就会从操作系统这里申请一大块内存空间,JVM接下来就要进一步的对这个大的空间进行划分,划分成不同区域,从而每个区域都有不同的功能作用,一共分为如下几个区域 1.堆…...
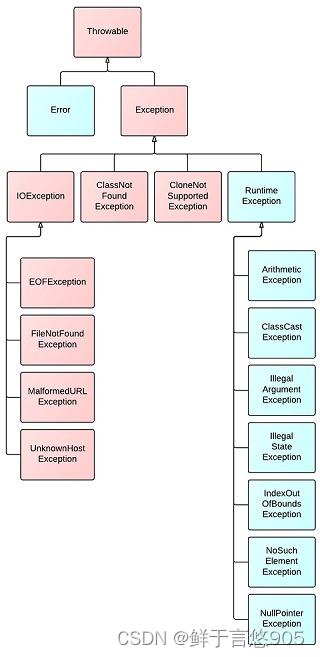
Java异常详解
Java异常详解 前言一、异常类的定义Java异常异常类的构成Java常见运行错误异常示例除以 0数组下标越界访问 null 对象 防御式编程异常的好处LBYL 风格的代码EAFP 风格的代码 二、异常的基本用法捕获异常基本语法代码示例不处理异常使用 try catch 后的程序执行过程catch 只能处…...
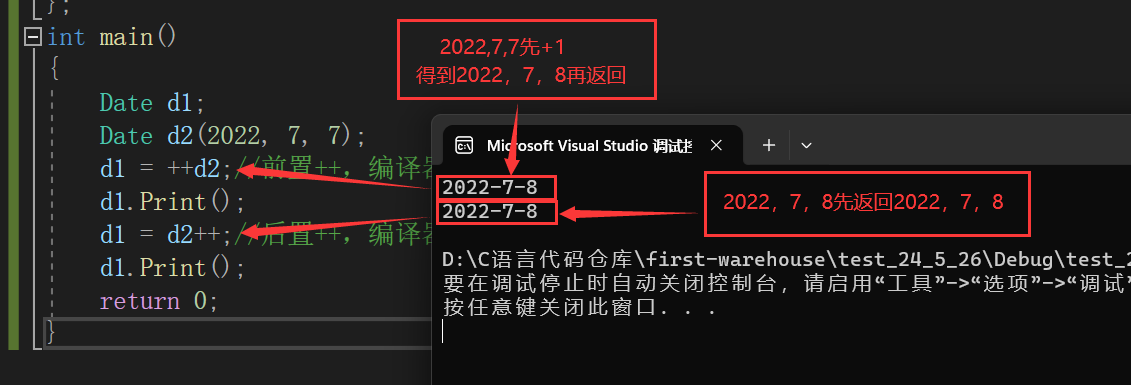
C++入门3——类与对象2(类的6个默认成员函数)
目录 1.类的6个默认成员函数 2. 构造函数 2.1 构造函数的概念 2.2 构造函数的特性 3. 析构函数 3.1 析构函数的概念 3.2 析构函数的特性 4.拷贝构造函数 4.1 拷贝构造函数的概念 4.2 拷贝构造函数的特性 5.赋值运算符重载函数 5.1运算符重载函数 5.2 赋值运算符重…...

CobaltStrike基本渗透
目录 CobaltStrike简介 主要功能: 使用注意: 在使用CobaltStrike进行渗透测试时,务必遵守法律法规,并获得合法授权。 CobaltStrike安装 前提 安装 服务端安装 windows安装 CS基本使用 监听器配置 一些基本的攻击…...
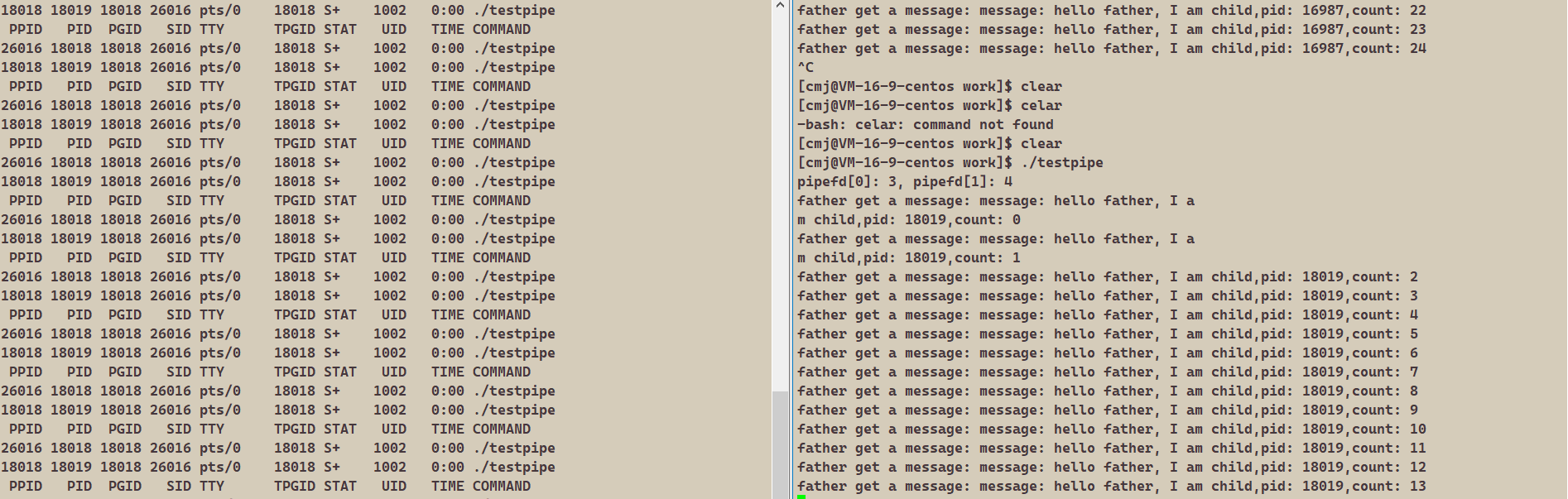
【linux深入剖析】进程间通信
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1.进程间通信目的2. 什么…...
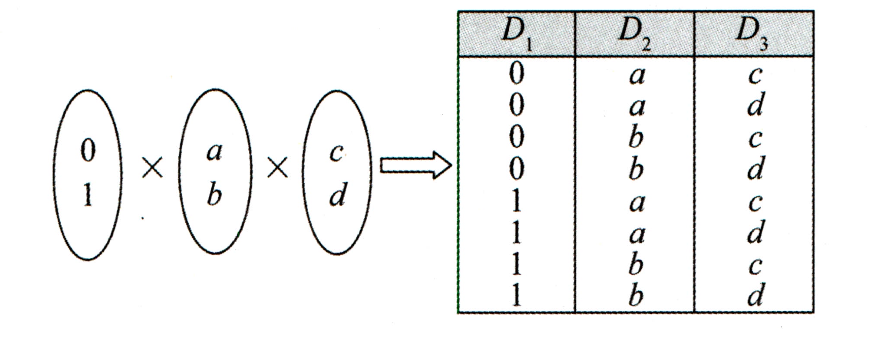
关系数据库:关系模式
文章目录 基本概述关系的相关名词术语笛卡儿积与关系关系的类型 关系模式总结 基本概述 关系的相关名词术语 关系:简单来说,就是一张二维表格。属性(Attribute):也称字段或列,在现实世界中,要描述一个事务常常取若干…...

医学图像处理质量的评价方法
评判处理后医学图像的质量是确保图像处理技术有效性和可靠性的关键。以下是一些常用的图像质量评估方法和指标: 1. 主观评估 主观评估是由专业人员(如放射科医生)通过视觉检查对图像质量进行评分。常用的主观评估方法包括: 视觉…...
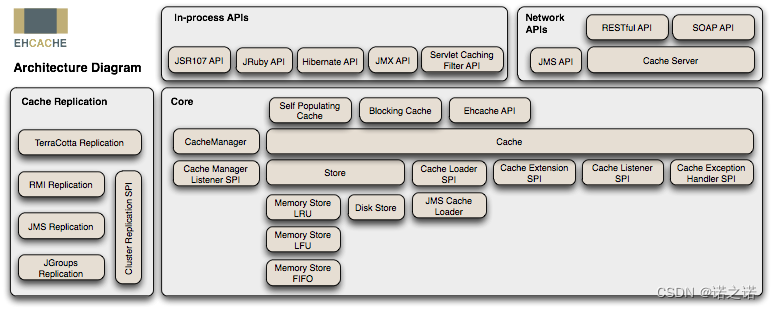
Ehcache Java 缓存框架
详解 下图是 Ehcache 在应用程序中的位置: Ecache 是一个广泛使用的 Java 缓存框架,能够有效提升应用性能,并减少与后端数据库的交互次数。它采用了一系列高级缓存策略,包括内存缓存、磁盘缓存、分布式缓存等,并提供了…...
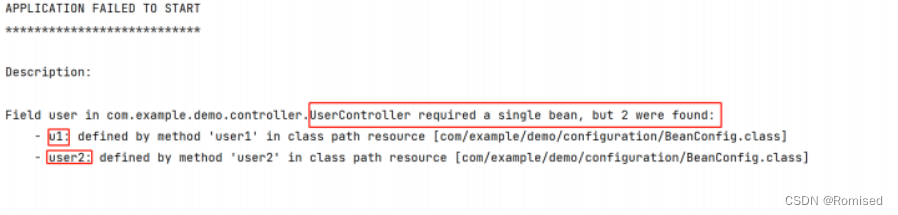
详解Spring IoCDI(二)
目录 承接上文:详解Spring IoC&DI (一) 1.IoC详解 1.1方法注解Bean 1.2方法注解要配合类注解使用 1.3定义多个对象 1.4重命名Bean 1.5扫描路径 2.DI详解 2.1DI与IoC的关系 2.2属性注入 2.3构造方法注入 2.4Setter注入 2.5 三…...

说明白计算机网络之TCP的流量控制与拥塞控制之慢开始算法与拥塞避免算法
TCP的流量控制 利用滑动窗口实现流量控制 设A向B发送数据,连接建立时候,B告诉A自身的接收窗口大小,A的发送窗口大小不能超过接收方B的窗口大小 流量控制:发送方发送速率不要太快,要让接收方来得及接收。窗口大小的单…...

这款信创FTP软件,可实现安全稳定的文件传输
信创,即信息技术应用创新,2018年以来,受“华为、中兴事件”影响,国家将信创产业纳入国家战略,并提出了“28n”发展体系。“8”具体指金融、石油、电力、电信、交通、航空航天、医院、教育等主要行业。目前企业使用比较…...

代码随想录算法训练营第十天|232.用栈实现队列、225. 用队列实现栈
232.用栈实现队列 题目链接:232. 用栈实现队列 文档讲解:代码随想录 状态:写出来 ,但差强人意 思路: 定义两个容器,可以是Stack,也可以是Deque,stackIn相当于临时容器,用来存放元素&…...
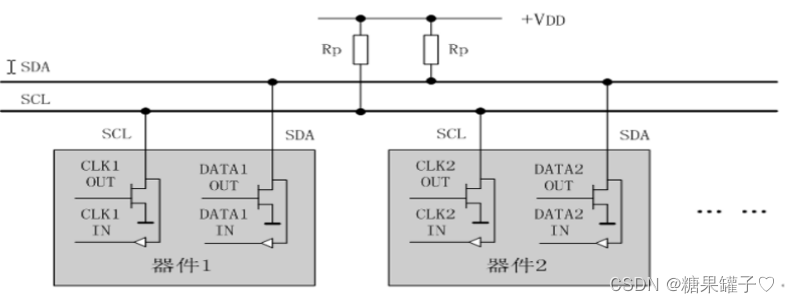
STM32 IIC协议
本文代码使用 HAL 库。 文章目录 前言一、什么是IIC协议二、IIC信号三、IIC协议的通讯时序1. 写操作2. 读操作 四、上拉电阻作用总结 前言 从这篇文章开始为大家介绍一些通信协议,包括 UART,SPI,IIC等。 UART串口通讯协议 SPI通信协议 一、…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
