从0开始学统计-什么是回归?
1.什么是回归?
回归(Regression)是统计学中一种用于探索变量之间关系的分析方法。它主要用于预测一个或多个自变量(输入变量)与因变量(输出变量)之间的关系。在回归分析中,我们尝试根据已知的自变量值来预测因变量的值。
回归分析通常用于以下情况:
(1) 预测:通过已知的自变量值来预测因变量的值。例如,根据房屋的面积、地理位置等因素来预测房屋的售价。
(2)关联性分析:确定自变量与因变量之间的关系强度和方向。例如,研究气温与冰淇淋销量之间的关系。
(3)控制变量:在研究中控制其他变量的影响,以便更准确地分析自变量与因变量之间的关系。
回归分析的基本思想是通过一个数学模型来描述自变量和因变量之间的关系。这个模型通常是一个线性函数,但也可以是其他形式,如多项式函数、指数函数等。常见的回归分析包括线性回归、多元线性回归、逻辑回归等。
在实际应用中,回归分析是数据科学和机器学习中的重要工具之一,广泛应用于预测、分类、控制和优化等领域。
弗朗西斯·高尔顿(Francis Galton)是19世纪的一位英国科学家,涉猎广泛,特别是在统计学、心理学和生物学方面做出了许多重要贡献。其中一个著名的贡献就是提出并发展了“回归”这一统计概念。
高尔顿在研究遗传学时,发现了一个有趣的现象,即子女的某些特征往往会回归到群体平均水平。例如,他观察到高个子父母的子女虽然也倾向于较高,但往往没有父母那么高;同样,矮个子父母的子女虽然也倾向于较矮,但往往没有父母那么矮。这一现象后来被称为“回归”或“回归均值”。
为了更好地理解这一现象,高尔顿进行了大量的数据分析和实验,并最终提出了“回归线”的概念。他的工作奠定了现代回归分析的基础,这是一种用于探讨和量化变量之间关系的重要统计方法。
具体来说,高尔顿的研究包括:
(1) 回归分析:高尔顿最初在研究身高遗传时注意到,子女的身高总是回归到平均水平。他利用散点图和回归线来描述这种趋势。这为后来的线性回归模型奠定了基础。
(2)相关系数:高尔顿还发展了相关分析的方法,用来量化两个变量之间的线性关系。卡尔·皮尔逊(Karl Pearson)进一步推广了这一概念,提出了皮尔逊相关系数。
高尔顿的贡献不仅在于他发现了这些现象,更在于他开发了统计工具和方法,使得其他科学家可以系统地研究和分析数据。这些工具和方法今天仍然广泛应用于各个科学领域。
2.回归和相关有什么区别?
回归分析和相关分析都是用于探索变量之间的关系,但它们有一些重要的区别:
(1)目标:
- 回归分析:旨在建立一个数学模型来描述自变量与因变量之间的关系,并用这个模型进行预测。回归分析关注的是预测性能,即模型在新数据上的表现。
- 相关分析:旨在衡量两个变量之间的相关程度,即它们的变化是否同步发生。相关分析关注的是变量之间的关联性,而不是因果关系或预测能力。
(2)用途: - 回归分析:通常用于预测一个或多个因变量的值,根据已知的自变量值。它可以用于预测连续型变量,也可以用于分类问题(例如逻辑回归)。
- 相关分析:用于描述和衡量两个变量之间的关系强度和方向。它可以帮助我们了解变量之间的相关性,但不能用于预测。
(3)统计方法: - 回归分析: 通常基于最小二乘法等统计方法来拟合一个数学模型,例如线性回归、多元线性回归、逻辑回归等。
- 相关分析: 通常使用皮尔逊相关系数或斯皮尔曼等级相关系数等统计量来衡量变量之间的相关性。
(4)变量类型: - 回归分析:可以用于分析和预测连续型变量之间的关系,也可以用于分析离散型因变量的关系(例如逻辑回归)。
- 相关分析:通常用于衡量两个连续型变量之间的关系。
虽然回归分析和相关分析有一些区别,但它们都是探索变量之间关系的重要工具,在统计学和数据分析中都具有广泛的应用。
3.回归的分类
回归分析根据自变量(解释变量)和因变量(响应变量)的数量以及模型的形式可以分为多种类型。以下是常见的回归分析分类:
(1)线性回归: - 简单线性回归:只有一个自变量和一个因变量的回归分析。
- 多元线性回归:有多个自变量和一个因变量的回归分析。
(2)非线性回归: - 多项式回归:自变量和因变量之间的关系可用多项式函数来描述。
- 指数回归:因变量的对数与自变量之间存在线性关系。
- 对数回归:自变量的对数与因变量之间存在线性关系。
- 幂函数回归:自变量和因变量之间存在幂函数关系。
(3)广义线性模型(Generalized Linear Models, GLM): - 逻辑回归:用于二分类问题,因变量是二元变量。
- 泊松回归:用于计数数据,因变量是计数型变量。
- 负二项分布回归:用于计数数据,对应因变量的方差大于均值的情况。
- Gamma 回归:用于因变量为连续的正数,但不是正态分布的情况。
(4) 岭回归和 Lasso 回归: - 岭回归(Ridge Regression):通过添加 L2 正则化项来解决多重共线性问题。
- Lasso 回归(Least Absolute Shrinkage and Selection Operator):通过添加 L1 正则化项来实现特征选择和稀疏性。
(5)弹性网络回归(Elastic Net Regression): - 综合了岭回归和 Lasso 回归的特点,同时使用 L1 和 L2 正则化项。
(6)加权回归(Weighted Regression): - 对不同观测值赋予不同的权重,以适应不同观测值的异方差性。
(7)非参数回归(Nonparametric Regression): - 不假设数据遵循特定的分布或模型形式,根据数据来拟合灵活的曲线。
(8)稳健回归(Robust Regression): - 对异常值具有鲁棒性,减少异常值对回归结果的影响。
以上是一些常见的回归分析类型,每种类型适用于不同的问题和数据特征。选择适当的回归模型是根据数据类型、假设和分析目的来决定的。
4.回归分析的步骤
(1)数据收集
收集要分析的变量数据。例如,在上一篇中,我们收集了温度和游客数量。
温度(x):20,23,26,29,30,33,35,38
游客数量(y):80,120,270,430,540,580,680,750
(2)数据可视化
绘制散点图来初步观察变量之间的关系。这有助于判断是否存在线性关系或其他类型的关系。

(3)假设模型
选择适当的回归模型。这里我们以简单线性回归为例:




可以有很多条线来拟合这些点,那么如何判断哪条线最好呢?

对于简单线性回归,这些参数的计算公式如下:


(4)估计模型参数



(计算结果来自chatgpt,不一定准确,只看步骤就行)
(5) 模型评估
计算决定系数 (𝑅2) 和进行残差分析

(残差分析这里只提一下,后面碰到再详细说)

(6) 假设检验
进行 t 检验以确定 𝑎和 𝑏 是否显著。

解释一下这里面几个要计算的量


截距和斜率标准误差的计算公式:


然后计算t统计量,查找临界值就行了。


(7)预测和解释

(8) 报告结果

(计算结果来自chatgpt,不一定准确,只看过程就行了)
用代码简单一些:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats# 数据输入
temperature = np.array([20, 23, 26, 29, 30, 33, 35, 38])
visitors = np.array([80, 120, 270, 430, 540, 580, 680, 750])# 绘制散点图
plt.figure(figsize=(10, 6))
plt.scatter(temperature, visitors, color='blue', label='Data Points')
plt.xlabel('Temperature (°C)')
plt.ylabel('Number of Visitors')
plt.title('Scatter Plot of Temperature vs. Number of Visitors')
plt.legend()
plt.grid(True)
plt.show()# 回归模型拟合
slope, intercept, r_value, p_value, std_err = stats.linregress(temperature, visitors)
print(f'回归方程: y = {intercept:.2f} + {slope:.2f}x')# 绘制回归函数图
plt.figure(figsize=(10, 6))
plt.scatter(temperature, visitors, color='blue', label='Data Points')
plt.plot(temperature, intercept + slope * temperature, color='red', label='Regression Line')
plt.xlabel('Temperature (°C)')
plt.ylabel('Number of Visitors')
plt.title('Regression Line of Temperature vs. Number of Visitors')
plt.legend()
plt.grid(True)
plt.show()# 决定系数
r_squared = r_value**2
print(f'决定系数 (R^2): {r_squared:.4f}')# 残差分析
predicted_visitors = intercept + slope * temperature
residuals = visitors - predicted_visitorsplt.figure(figsize=(10, 6))
plt.scatter(temperature, residuals, color='purple')
plt.axhline(y=0, color='red', linestyle='--')
plt.xlabel('Temperature (°C)')
plt.ylabel('Residuals')
plt.title('Residual Plot')
plt.grid(True)
plt.show()# 残差的统计量
residuals_mean = np.mean(residuals)
residuals_std = np.std(residuals)
print(f'残差的平均值: {residuals_mean:.4f}')
print(f'残差的标准差: {residuals_std:.4f}')# 斜率和截距的t统计量
t_stat_slope = slope / std_err
t_stat_intercept = intercept / (std_err * np.sqrt(np.sum((temperature - np.mean(temperature))**2)))
print(f'斜率的 t 统计量: {t_stat_slope:.4f}')
print(f'截距的 t 统计量: {t_stat_intercept:.4f}')# 计算斜率和截距的p值
p_value_slope = 2 * (1 - stats.t.cdf(np.abs(t_stat_slope), df=len(temperature)-2))
p_value_intercept = 2 * (1 - stats.t.cdf(np.abs(t_stat_intercept), df=len(temperature)-2))
print(f'斜率的 p 值: {p_value_slope:.4f}')
print(f'截距的 p 值: {p_value_intercept:.4f}')
得到的结果:




相关文章:

从0开始学统计-什么是回归?
1.什么是回归? 回归(Regression)是统计学中一种用于探索变量之间关系的分析方法。它主要用于预测一个或多个自变量(输入变量)与因变量(输出变量)之间的关系。在回归分析中,我们尝试根…...
Element-ui使用上传时弹框选择文件类型
实现效果 1,点击上传,上传文件; 2,选择文件; 3,弹框选择文件类型; 4,选择类型后确定上传; 一,上传 跳过; 二,定义弹框下拉框…...

原生小程序一键获取手机号
1.效果图 2.代码index.wxml <!-- 获取手机号 利用手机号快速填写的功能,将button组件 open-type 的值设置为 getPhoneNumber--><button open-type"getPhoneNumber" bindgetphonenumber"getPhoneNumber">获取手机号</button> …...
ARM虚拟机安装OMV
OMV(OpenMediaVault)是基于 Debian GNU/Linux 的网络连接存储(network attached storage,NAS)解决方案。它包含 SSH、(S) FTP、SMB/CIFS、DAAP 媒体服务器、rsync、 BitTorrent 等很多种服务。它可用于 x86-64 和 ARM 平台。 在x86-64平台上&…...

【协议开发系列】梳理关于TCP和UDP两种协议的区别和使用场景
起源 前二天项目上在核对外部对接服务的五元组列表的时候,有一位客户提问对于同样的服务同时支持tcp和udp二种方式,有什么优点和缺点,应该如何选择?这个问题突然让我愣了一下,确实好久没有“温故”了,相关…...

vue blob实现自定义多sheet数据导出到excel文件
背景:最近vue项目遇到一个需求,就是需要将多个表格分成不同sheet页并导出,之前的工具类只能导出一个sheet页,所以在原有的基础上,调整一下,让它支持多sheet导出。 vue blob文件流,这个肯定要的…...

Python—面向对象小解(3)
一、多态 多态指的是一类事物的多中形态 相同的方法,产生不同的执行结果 运算符 * 的多态 int int 加法计算 str str 字符串拼接 list list 列表的数据合并 在python中可以使用类实现一个多态效果 在python中使用重写的方式实现多态 (1)定…...

Nginx超时时间
Nginx是一款自由、开源、高性能的HTTP和反向代理服务器,它可以通过不同的设置来提高网站的性能和安全性。其中,设置Nginx超时时间非常重要,因为它将直接影响网站的响应速度和用户体验。本文将从多个方面详细阐述Nginx超时时间的设置方法与注意…...

Imgs,GT,Edge,Gradient_all,Gradient_Foreground
保存一下: 做个记录: import cv2 import os import numpy as np# 对整张图片做canny检测 得到纹理图 def canny_all(input_path, output_path):# 遍历文件夹中的所有文件for filename in os.listdir(input_path):# 构造完整的文件路径image_path os.p…...

自学成才Flutter 弹性布局、线性布局
本文我们要介绍 Flutter 中布局 Widget,包括弹性布局、线性布局 流式布局和层叠布局。 Flutter中文网 Flutter开发 一、弹性布局--Flex Flex 类似 Android 中的 FlexboxLayout,和 Expanded 配合使用可以实现子Widget 按照一定比例来分配父容器空间。 使…...
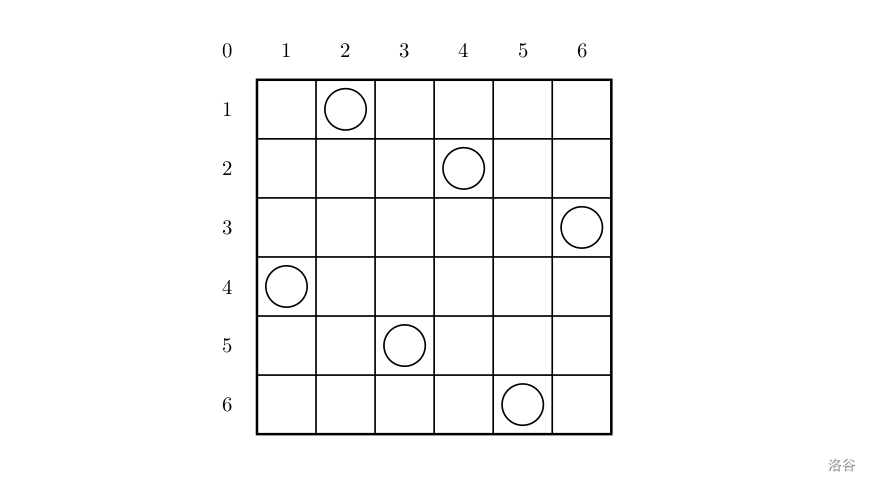
Part 3.1 深度优先搜索
深度优先搜索(DFS),即按照深度优先的顺序搜索的算法。 深度优先搜索一般使用栈来实现。 [USACO1.5] 八皇后 Checker Challenge 题目描述 一个如下的 6 6 6 \times 6 66 的跳棋棋盘,有六个棋子被放置在棋盘上,使得…...
前端Vue小兔鲜儿电商项目实战Day03
一、Home - 整体结构搭建和分类实现 1. 页面结构 ①按照结构新增5个组件,准备最简单的模板,分别在Home模块的入口组件中引入 src/views/Home/components/ HomeCategory.vue HomeBanner.vue HomeNew.vue HomeHot.vue HomeProduct.vue <script …...

ORACLE 查询SQL优化
1 使用EXPLAIN PLAN 使用EXPLAIN PLAN查看查询的执行计划,这可以帮助你理解查询是如何被Oracle执行的。基于执行计划,你可以确定是否存在索引缺失、不必要的全表扫描等问题。 以下是几种使用EXPLAIN PLAN的方法: 使用EXPLAIN PLAN FOR: 你可以…...
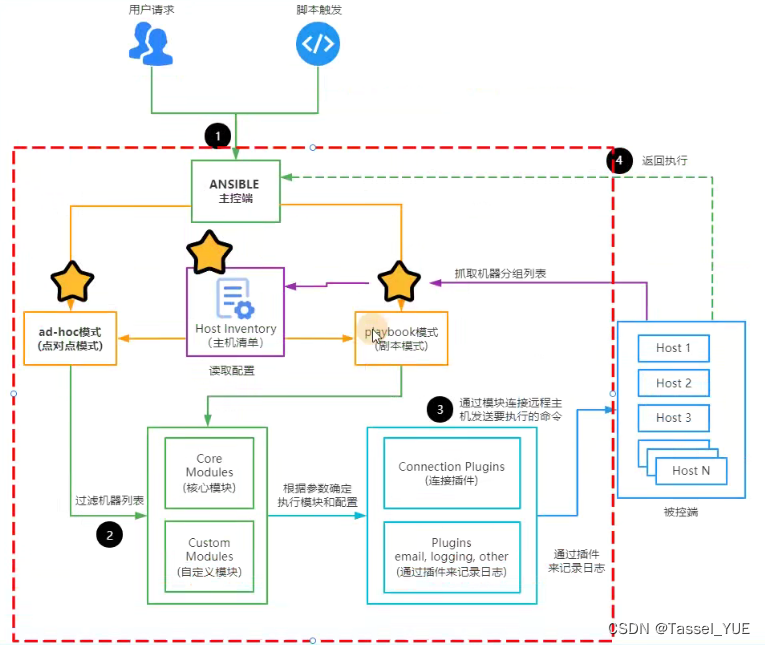
Ansible03-Ansible Playbook剧本详解
目录 写在前面5. Ansible Playbook 剧本5.1 YAML语法5.1.1 语法规定5.1.2 示例5.1.3 YAML数据类型 5.2 Playbook组件5.3 Playbook 案例5.3.1 Playbook语句5.3.2 Playbook1 分发hosts文件5.3.3 Playbook2 分发软件包,安装软件包,启动服务5.3.3.1 任务拆解…...

Qt-qrencode生成二维码
Qt-qrencode开发-生成二维码📀 文章目录 Qt-qrencode开发-生成二维码📀[toc]1、概述📸2、实现效果💽3、编译qrencode🔍4、在QT中引入编译为静态库的QRencode5、在Qt中直接使用QRencode源码6、在Qt中使用QRencode生成二…...
)
长安链使用Golang编写智能合约教程(三)
本篇主要介绍长安链Go SDK写智能合约的一些常见方法的使用方法或介绍 资料来源: 官方文档官方示例合约库 官方SDK接口文档 教程一:智能合约编写1 教程二:智能合约编写2 一、获取参数、获取状态、获取历史记录的方法解析 注意! …...
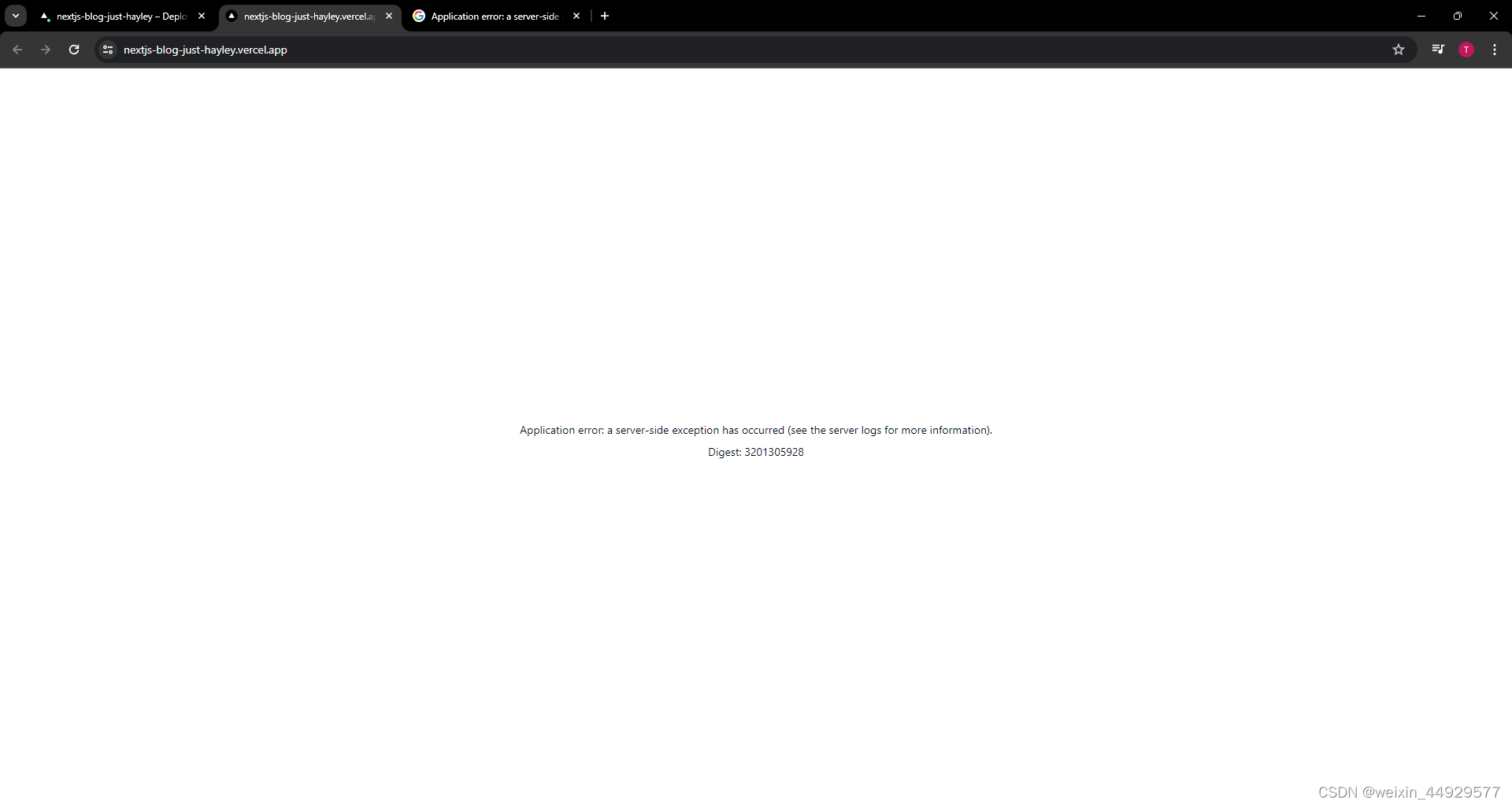
Vercel deploy- Nextjs project error-URL link-env variable
Vercel deploy- Nextjs project error-URL link-env variable Error Check Database URL Check next-auth URL NEXTAUTH_URLhttps://yourappname.vercel.app/ 依次排查可能性 Application error: a server-side exception has occurred (see the server logs for more in…...

Java | Leetcode Java题解之第123题买卖股票的最佳时机III
题目: 题解: class Solution {public int maxProfit(int[] prices) {int n prices.length;int buy1 -prices[0], sell1 0;int buy2 -prices[0], sell2 0;for (int i 1; i < n; i) {buy1 Math.max(buy1, -prices[i]);sell1 Math.max(sell1, b…...

Ubuntu22.04之扩展并挂载4T硬盘(二百三十三)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

Redis实现延迟队列
最近用到一个延迟消息的功能,第一时间想到使用MQ或者MQ的插件,因为数据量不大,所以尝试使用Redis来实现了,毕竟Redis也天生支持类似MQ的队列消费,所以,在这里总结了一下Redis实现延迟消息队列的方式。 一、…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
